How do Machines Keep Secrets III
Ryan: FYS Computational Reasoning Fall 2025
Lecture content licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Dan's 0ld Module Intro
Dan's 0ld Readings Intro
Cryptography & Secrets Videos
REFERENCES/RESOURCES
Secrets
Blockchain, Bitcoin
Blockchain in Javascript
IMAGES
CHAPTER 1

What is blockchain? Depends whom you ask.

Computer Scientist
What is blockchain? Depends whom you ask.

Accountant
DISTRIBUTED
PUBLIC LEDGER of PEER-TO-PEER TRANSACTIONS.
What is blockchain? Depends whom you ask.

Activist
TRUSTLESS, BORDERLESS, OPEN, DECENTRALIZED, PUBLIC, UNCHANGEABLE record of TRANSACTIONS
BORDERLESS
OPEN
TRUSTLESS
DECENTRALIZED
UNCHANGEABLE
PUBLIC
PEER-TO-PEER
DISTRIBUTED
LEDGER
TRANSACTIONS
TRUSTLESS participants do not need relational connection with transaction partners as any behavior they'd want a guarantee about is guaranteed by the system
BORDERLESS a blockchain is not physically located in one place and so it's unbound by geography and jurisdiction
OPEN refers to the software that runs the system being open
DECENTRALIZED: there is not a host or company or government in charge of the thing.
UNCHANGEABLE: once a transaction has been recorded in the ledger it cannot be changed without unraveling the whole thing.
PEER-TO-PEER means the transactions are between sender and receiver without a "middle man"
DISTRIBUTED means the software and the ledger does not reside on a single server. Everyone can have a copy of the ledger.
a LEDGER is a record of all the transactions in a system
TRANSACTIONS: anything we want a record of can be a transaction, but for now, A sends $X to B
LINKED LIST a data structure in which each element "points" to its predecessor and/or successor.
PUBLIC refers to the fact that the information on the blockchain is visible to the public - it can be hashed or encrypted but the outline of the transaction is visible
Ch 4 Money
4 Money: Can I pay You $10 with Serial Number?
Can I Pay You by Texting You the Serial Number?


What if instead of this...
on 06Oct2025 Cal gave PE25377707B to Dan on 19Sep2025 Bri gave PE25377707B to Cal on 10Sep2025 Ali gave PE25377707B to Bri on 18JUL2025 GOD gave PE25377707B to Ali
Answer: you look in the ledger




Cal Dan
6 Oct
Bri Cal
19 Sept
Ali Bri
10 Sept
GOD Ali
18 July




...we had this.
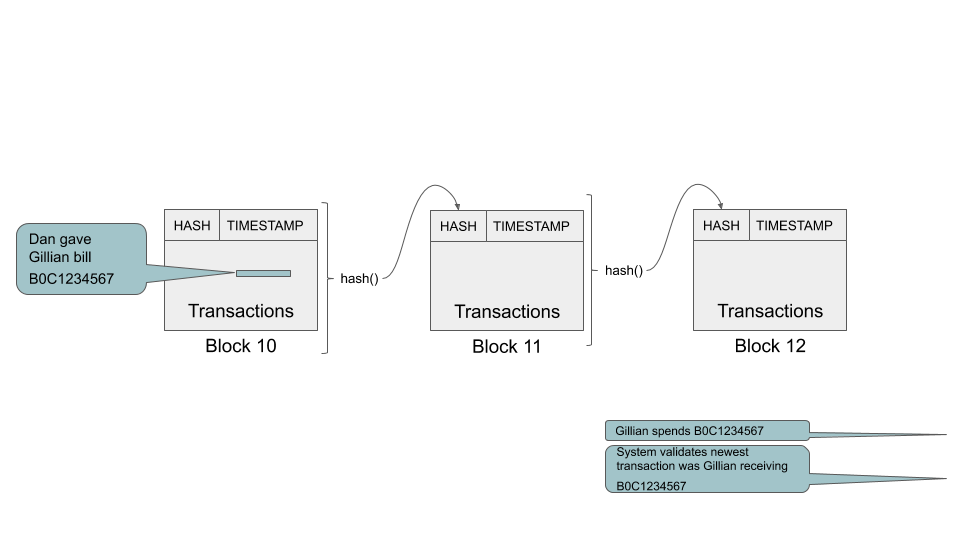
How does D know A, B or C hasn't given the number to someone else?
When I engage in a transaction I tell the whole world about it:
Dan sends Eve 50 dollars PE2577707B
But how does everyone know the message is from me?
We have a tool for that!
I use my private key to encrypt it and everyone who has my public key can verify the message came from me.
Transaction: Dan sends Eve $5
Encrypt(
Dan sends Eve $5
, DanPrivateKey
)
This means everyone's copy of the ledger can be correct
But can't someone fiddle with the ledger...?
We have a tool for that!
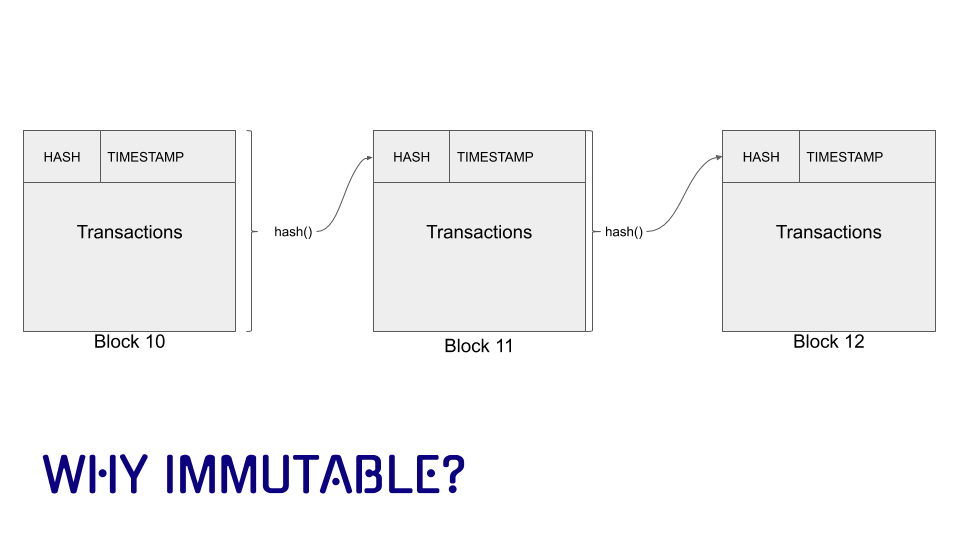
How hard is it, though, to just redo the ledger?
We have a answer for that!

Make it really hard to recompute the hash
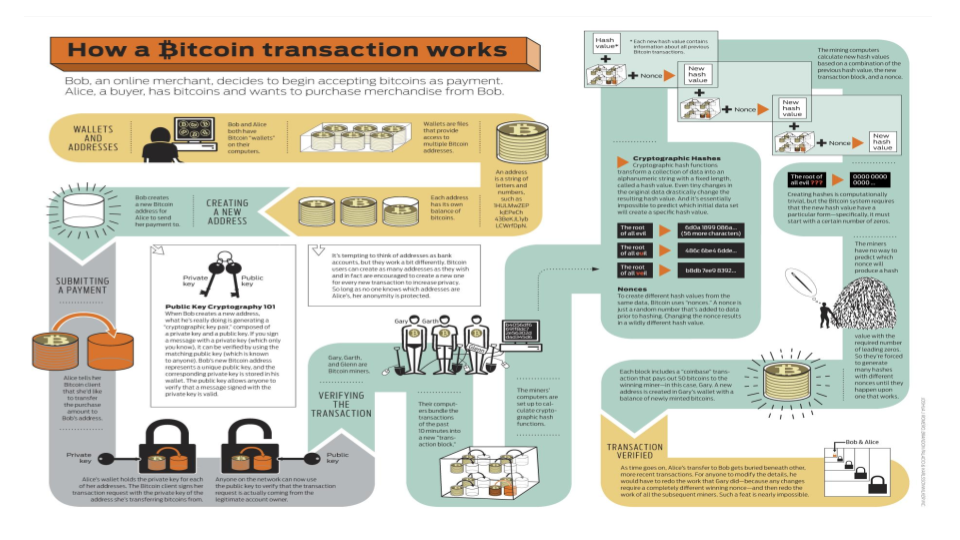
Person A: Why can’t I just pay someone by telling them a fifty-dollar bill’s serial number from my wallet?
Person B: Because someone else could tell the same serial number to another person — you could double-spend it.
Person A: So we write it down in a public ledger.
Person B: Then how do you stop someone from changing the ledger later?
Person A: What if everyone has a copy of the ledger?
Person B: Great — now everyone can check. And they can vote if there is a discrepancy. How does a copy get updated when you make a payment?
Person A: I announce: “Dan sent Evan $50 — bill PE277707B — Tuesday, Oct 17.”
Person B: How do they know that announcement is actually from you and not an impersonator?
Person A: I sign the transaction with my private key. Everyone uses my public key to verify the signature.
Person B: Okay, but someone could still alter copies of the ledger afterwards.
Person A: What if each day we compute a hash summarizing that day’s transactions and include it in the next day’s record — so every day is linked to the previous?
Person B: Then if someone changed yesterday’s transactions, the hash would change and your link would break. But an attacker could recalculate the hashes for all following days and pretend nothing happened.
Person A: So make hashing expensive. If each block takes a lot of work to compute, redoing the work for one block — and every block after it — becomes prohibitively costly.
Person B: That’s the idea behind proof-of-work: it makes rewriting history expensive, and the network follows the longest/heaviest valid chain so honest participants keep the ledger consistent.
Paper-chain exercise: students write “transactions” on slips, compute a simple hash (e.g., sum of ASCII values mod 100), link slips by including previous hash, then try to alter an old slip and see how many subsequent hashes they must recompute.
A gives B X written as AB55
HASH 65*1+66*2+53*3+53*4=564
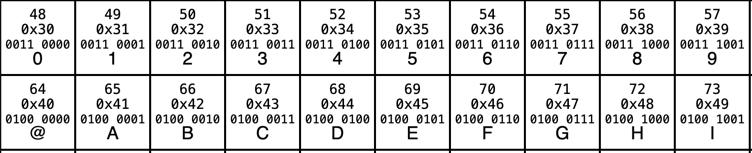
Simple world with code system consisting of 10 digits and 10 letters (A-I). The letters stand for people. Assets are numbered 001, 002, etc. A transaction has a from person, a to person, and an asset identifier
AB001.
The digits have encodings equal to their value and the encodings of the letters begin with A=10.
Hashing is simply the encoded value of a character times its position in the text being hashed mod 100. So AB001 would be
1*1 + 2*2 + 0*3 + 0*4 + 1*5=10. If a block has multiple transactions we treat them like one long string. After the first block, each starts with the hash of the previous block.
When we want to make the hash hard we require that it be less than 10 when nonce is appened to text.
Attack roleplay: split class into honest nodes and an attacker; let them try to double-spend and see how the group resolves conflicting chains with a rule (longest chain wins).
Part 1 — The Public Ledger Problem
Scenario
You and your classmates each “own” a few digital $10 bills, identified by serial numbers (like PE25377707B).
You can write transactions like:
“Maya pays Sam $10 (bill PE25377707B).”
Question:
What problems could happen if everyone just shouted transactions aloud without keeping records?
What if only one person keeps the ledger?
What if everyone keeps a copy?
(Goal: set up the idea of distributed ledgers and double-spending.)
Part 2 — Linking Blocks with Hashes
Each “block” represents a day’s transactions.
Example:
Compute a toy hash
Add up the ASCII codes or letter values (A=1…Z=26) for all letters/numbers in the transactions.
Then take the last two digits of the total.
Write that as your block’s “hash.”
Example: Total = 1234 → Hash = 34.
Link the next block
Write a new block of transactions, but include the previous block’s hash at the top.
Compute this block’s new hash the same way.
Now tamper with history
Change one word in the first block (“Maya” → “Naya”).
What happens to all the later hashes?
Part 4 — Consensus & Trust
If two groups of students have slightly different chains, which should the class accept?
Rule: the chain that required the most work (i.e., the longest valid chain).
Discuss:
What happens if one person controls most of the computing power?
Why is trust distributed instead of centralized?
Part 5 — Quick Takeaway
Blockchains combine digital signatures, linked hashes, and costly verification so everyone can agree on one shared history — even when they don’t trust each other.


6 Blockchain 2

How Machines Keep Secrets III
By Dan Ryan
How Machines Keep Secrets III
- 116




