Repetition
Lecture content licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.

Go Play with Recursive Drawing
Repetition
Contents
Chapter 1: Reflexes and Repertoire
1. “I wonder if problem can be solved by repetition….”
-
Repertoire
-
Reflexes
3. Big O
3. How big is this problem?
2. Is big problem actually a set of small problems?
2. Recursion
1. Nested loops
4. Backtracking, heuristics, divide and conquer, dynamic programming


How Do We Get From
THIS
TO
THIS
Repetition
in
Everyday Life

STOP+THINK
Why do we think this works?
Why is this chemistry in the 21st century?
STOP+THINK
STOP+THINK
How
does nature
do this?

STOP+THINK
or this?



Iteration
Repetition
Dissecting Repetition
"Lather, rinse, repeat."
Turns Out Lots of Life's Problems
Can Be Solved with Repetition
"Iterate. Iterate. Iterate."
"Scrub until clean."
"Season to taste."
"Keep trying until you get it right."
Which is the repetition of design?
Why Repetition & Strategy?
One of the readings for this week was Filho's chapter called "Strategy." What's the connection? In ch 3 Filho presents seven ideas that can be thought of as approaches to problem solving via algorithms. Hence, strategy - the ideas are overarching plans of attack, generic styles of bringing computational power to bear on a problem via an algorithm. The ideas are meta-algorithms or algorithmic families. And every one of them is a way of deploying repetition in a controlled manner.
Iteration
SOLUTION
PROBLEM
Adding FOR LOOPs to Our Repertoire
WHILE A DO B
B
A
LOOP
WHILE A DO B
B
A
LOOP
REPEAT B UNTIL A
A
B
LOOP
What if our stopping condition is simply a count?
function swim400()
lapCount = 0
while lapCount < 8
swim-50m-lap
increment lapCount
FOR I from 0 to 7 DO B
B
i=0
i<8
i=i+1
LOOP
"increment"
the loop counter
"initialize" the loop counter

A FOR loop is basically "while counter is below limit do something and increment counter."
B
i=0
i<8
i=i+1
LOOP
JavaScript SideBar

B
i=0
i<8
i=i+1
LOOP

LOOP
FOR
FOR
i=0
i<5
i++
B
LOOP
B
i=0
i<5
i++
LOOP
i=0
i<8
i++
FOR
for
B
LOOP
B
i=0
i<5
i++
LOOP
i=0
i<8
i++
FOR
for
B
( ; ; ) {
}
LOOP
FOR
for
block of statements to iterate over
(loop control specifications) {
}
practice
set colour black
for i from 1 to 3
paint i squares
switchColour
for (i=1; i<3; i++) {
//block of statements
}
black
paint i squares
switchC
i++
i<4?
i = 4
set colour black
for i from 1 to 3
paint i squares
switchColour
black
paint i squares
switchC
i++
i<4?
i = 4
set colour black
for i from 1 to 3
paint i squares
switchColour
black
paint i squares
switchC
i++
i<4?
i = 1
set colour black
for i from 1 to 3
paint i squares
switchColour
black
paint i squares
switchC
i++
i<4?
i = 1
set colour black
for i from 1 to 3
paint i squares
switchColour
black
paint i squares
switchC
i++
i<4?
i = 1
set colour black
for i from 1 to 3
paint i squares
switchColour
black
paint i squares
switchC
i++
i<4?
i = 1
set colour black
for i from 1 to 3
paint i squares
switchColour
black
paint i squares
switchC
i++
i<4?
i = 1
set colour black
for i from 1 to 3
paint i squares
switchColour
black
paint i squares
switchC
i++
i<4?
i = 1
set colour black
for i from 1 to 3
paint i squares
switchColour
black
paint i squares
switchC
i++
i<4?
i = 1
set colour black
for i from 1 to 3
paint i squares
switchColour
black
paint i squares
switchC
i++
i<4?
i = 2
set colour black
for i from 1 to 3
paint i squares
switchColour
black
paint i squares
switchC
i++
i<4?
i = 2
set colour black
for i from 1 to 3
paint i squares
switchColour
black
paint i squares
switchC
i++
i<4?
i = 2
set colour black
for i from 1 to 3
paint i squares
switchColour
black
paint i squares
switchC
i++
i<4?
i = 2
set colour black
for i from 1 to 3
paint i squares
switchColour
black
paint i squares
switchC
i++
i<4?
i = 2
set colour black
for i from 1 to 3
paint i squares
switchColour
black
paint i squares
switchC
i++
i<4?
i = 2
set colour black
for i from 1 to 3
paint i squares
switchColour
black
paint i squares
switchC
i++
i<4?
i = 2
set colour black
for i from 1 to 3
paint i squares
switchColour
black
paint i squares
switchC
i++
i<4?
i = 3
set colour black
for i from 1 to 3
paint i squares
switchColour
black
paint i squares
switchC
i++
i<4?
i = 3
set colour black
for i from 1 to 3
paint i squares
switchColour
black
paint i squares
switchC
i++
i<4?
i = 3
set colour black
for i from 1 to 3
paint i squares
switchColour
black
paint i squares
switchC
i++
i<4?
i = 3
set colour black
for i from 1 to 3
paint i squares
switchColour
black
paint i squares
switchC
i++
i<4?
i = 3
set colour black
for i from 1 to 3
paint i squares
switchColour
black
paint i squares
switchC
i++
i<4?
i = 3
set colour black
for i from 1 to 3
paint i squares
switchColour
black
paint i squares
switchC
i++
i<4?
i = 3
set colour black
for i from 1 to 3
paint i squares
switchColour
black
paint i squares
switchC
i++
i<4?
i = 4
set colour black
for i from 1 to 3
paint i squares
switchColour
black
paint i squares
switchC
i++
i<4?
i = 4
set colour black
for i from 1 to 3
paint i squares
switchColour
EXIT
black
paint i squares
switchC
i++
i<4?
i = 4
set colour black
for i from 1 to 3
paint i squares
switchColour
EXIT
set colour black
for i from 1 to 3
paint i squares
switchColour
colour = black;
for (i=1; i<3; i++) {
paint(colour,i)
}
if (colour == red) {
colour = black}
else {
colour = red};
initialize brush colour as black
initialize count variable i to 1
set limit for i
test i against limit
paint i squares in current colour
increment i
brush can be red or black
change colour of brush
if limit test OK
SO FAR
A third kind of loop flow: the "FOR LOOP"
In JS
for (counter=0; counter++; counter<limit) {
}
commands to be repeated;
Next
NESTED FOR LOOPS
How to Traverse a Chess Board
forward 1
start next row
repeat 8x
repeat 8x
How to Traverse a Chess Board
//visit square
//next row
for (col=0; col<8; col++){
}
for (row=0; row<8; row++) {
}
//visit square
//next row
for (col=0; col<8; col++){
}
for (row=0; row<8; row++) {
}
the INSIDE LOOP
the OUTSIDE LOOP
//visit square
//next row
for (col=0; col<8; col++){
}
for (row=0; row<8; row++) {
}
the INSIDE LOOP
the OUTSIDE LOOP
STOP+THINK: Which loop gets executed more times?
The inside loop.
The inside repetition is itself repeated.
Another
Example
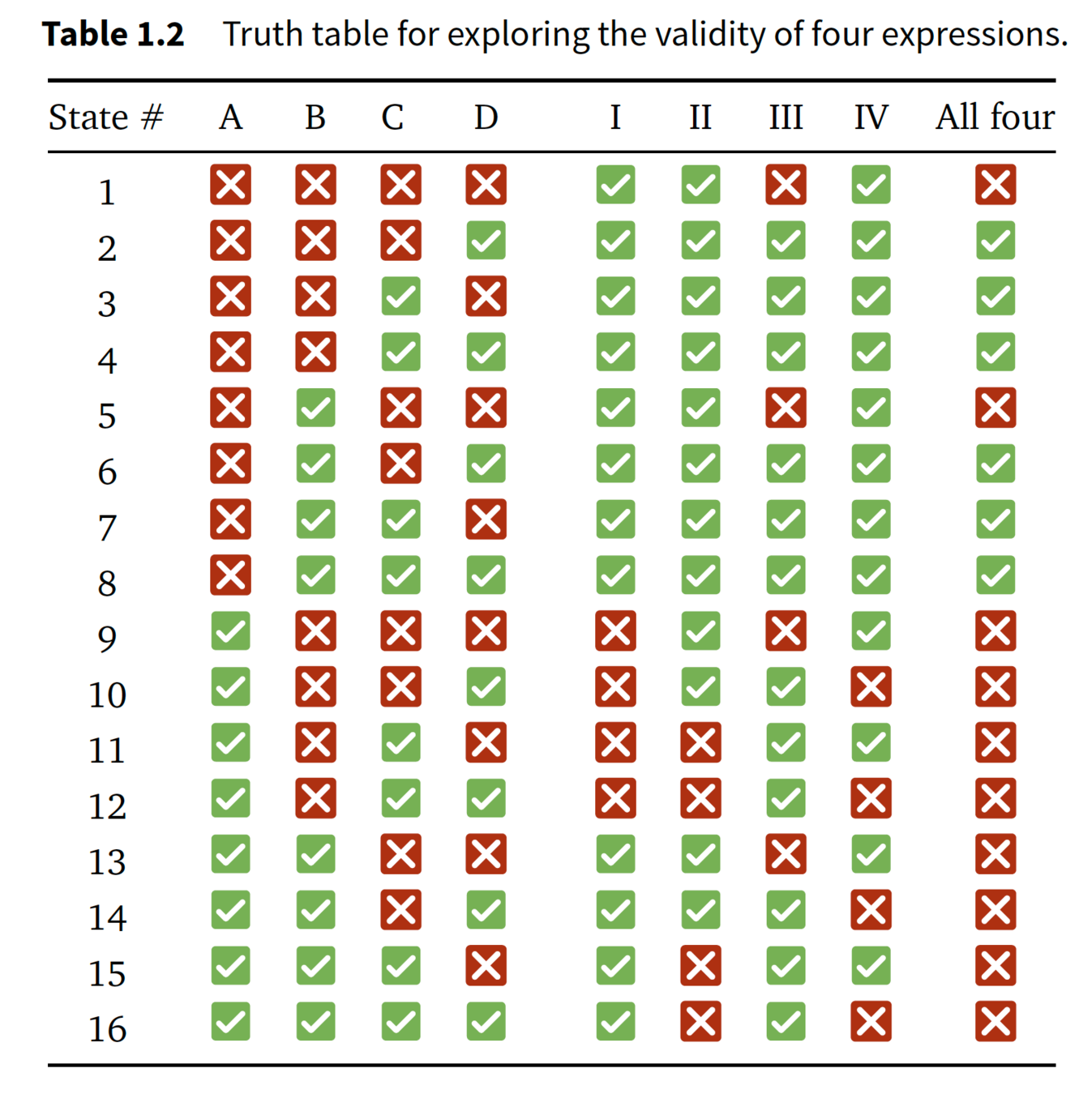
Truth Table and Nested Loops
STOP+THINK: What does this pseudocode do?
for A=1 to 0
for B=1 to 0
for C=1 to 0
print A, B, C
go to next line
1
1
1
↩
1 1 0 ↩
1 0 1 ↩
1 0 0 ↩
0 1 1 ↩
0 0 0 ↩
0 0 1 ↩
0 1 0 ↩
TL;DR
Truth Table
is a
Power Set
The Power Set


"for each" is like a for loop but instead of counting 1, 2, 3 it does one iteration for each member of some category or set
a SET is a new data type for us

The Power Set

create "fragrances" as a new (empty) "set"
create a new (empty) "set" and add it to fragrances
"flowers" is a set of flower ingredients
for each flower
make a copy of the fragrances set
for each item in the copy of fragrances
add the flower to it
combine the old fragrances and the copy

How to Read this Pseudocode
the input to this function is a set of flowers
create a new (empty) set
call it "fragrances"
create another empty set
add to fragrances
for each flower in flowers repeat this
make a copy of the set fragrances
call it new_fragrances
for each set in new_fragrances
add this flower
combine new_fragrances & fragrances
return the set fragrances
the arrow means "take the value on the right and stick it in the thing on the left"
Set refers to the definition of sets and Set.new is how the system creates a new set
1
1
1
1
1
0
1
1
1
1
1
1
0
1
1
1
1
1
0
1
1
1
1
0
1
1
1
0
1
1
1
1
0
1
1
1
0
0
1
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
The Power Set and the Truth Table
1
1
1
1
1
0
1
1
1
1
1
1
0
1
1
1
1
1
0
1
1
1
1
0
1
1
1
0
1
1
1
1
0
1
1
1
0
0
1
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
The Power Set and the Truth Table
1
1
1
1
1
0
1
1
1
1
1
1
0
1
1
1
1
1
0
1
1
1
1
0
1
1
1
0
1
1
1
1
0
1
1
1
0
0
1
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
The Power Set and the Truth Table
Nested For Loops
let us solve problems and carry out tasks by exhaustion or brute force

Nested Loops: Stop+Think

Nested Loops: Stop+Think

3 rows of
3 columns of
2 rows of
2 columns of
1 row of
2 triangles


JULY 6, 2018
Automating molecule design to speed up drug development
by Rob Matheson, Massachusetts Institute of Technology
How Long Does It Take to make a quilt that is twice as large??
Size of Quilt
Time to Make






O(n2)
But Sometimes We Can Reduce the Work
Sort These Cards

cards[0]
cards[4]
cards[3]
cards[2]
cards[1]
Sort These Cards

cards[0]
cards[4]
cards[3]
cards[2]
cards[1]
start on the left
compare card to neighbor
swap if first is larger
next card
for (i=0;i<cards.length-1; i++){
compare cards[i], cards[i+1]
swap if cards[i]>cards[i+1]
}
Sort These Cards
highest card
What's next?
for (i=0;i<4; i++)
cards[0]
cards[4]
cards[3]
cards[2]
cards[1]
cards[0]
cards[3]
cards[2]
cards[1]
cards[0]
cards[2]
cards[1]
cards[0]
cards[1]
for (i=0;i<3; i++)
for (i=0;i<2; i++)
for (i=0;i<1; i++)
Loop of Loops
for (j=4;j>0; j--) {
for (i=0;i<j; i++) { //something
}
}
NESTED FOR LOOPS
for (i=0;i<4; i++){ //something
}
for (i=0;i<3; i++){ //something
}
for (i=0;i<2; i++){ //something
}
for (i=0;i<1; i++){ //something
}
A Triangle Instead of a Square
How many steps?
N
N-1
N-2
N-3
...
1
N + N-1 + N-2 + ... + 3 + 2 + 1
1 + 2 + 3 + ... + N-2 + N-2 + N
N+1 + N+1 + N+1 + ... + N+1 + N+1 + N+1
Total = N(N+1)/2 = 1/2(N2+N)
O(n2)
Merge Two Sorted Lists
How many games will be played?

How many games will be played?


INSIGHT: All but one of the teams gets eliminated and one team gets eliminated in each game.
O(n)
Print a "Times Table"
function timesTable(n) {
for (i=0; i<n; i++) {
for (j=0; j<n; i++) {
//print i*j
}
//goto newline
}
timesTable(6) 1 2 3 4 5 6 2 4 6 8 10 12 3 6 9 12 15 18 4 8 12 16 20 24 5 10 15 20 25 30 6 12 18 24 30 36
timesTable(3) 1 2 3 2 4 6 3 6 9
O(n2)
So Far
- Lots of real world problems are iterative.
- We can implement iteration with "FOR" loops.
- JavaScript syntax of for loops.
- We can characterize iteration based on relation between number of steps and number of things we are dealing with.
- Nested for loops allow us to generate exhaustive list of combinations.
for (A=0; A<2; A++) {
for (B=0; B<2; B++) {
for (C=0; C<2; C++) {
for (D=0; D<2; D++) {
//evaluate expression
}
}
}
}
Same Idea in Filho's discusion of power sets

Sort These Cards

cards[0]
cards[4]
cards[3]
cards[2]
cards[1]
to sort 5 cards move the highest to the end sort 4 cards
to sort 4 cards move the highest to the end sort 3 cards
to sort 3 cards move the highest to the end sort 2 cards
to sort 2 cards move the highest to the end sort 1 cards
to sort 1 cards leave it be
Look Up a Word in the Dictionary
Find a Word in a Dictionary with N words
Find a Word in a Dictionary with N words
Split list in half
Is target in front or back half?
Split that half in half
Is target in front half or back half?
STOP+THINK: For how long can this go on?
Find a Word in a Dictionary with N words
STOP+THINK: For how long can this go on?
N > N/2 > N/4 > N/8 > ... 1 and DONE
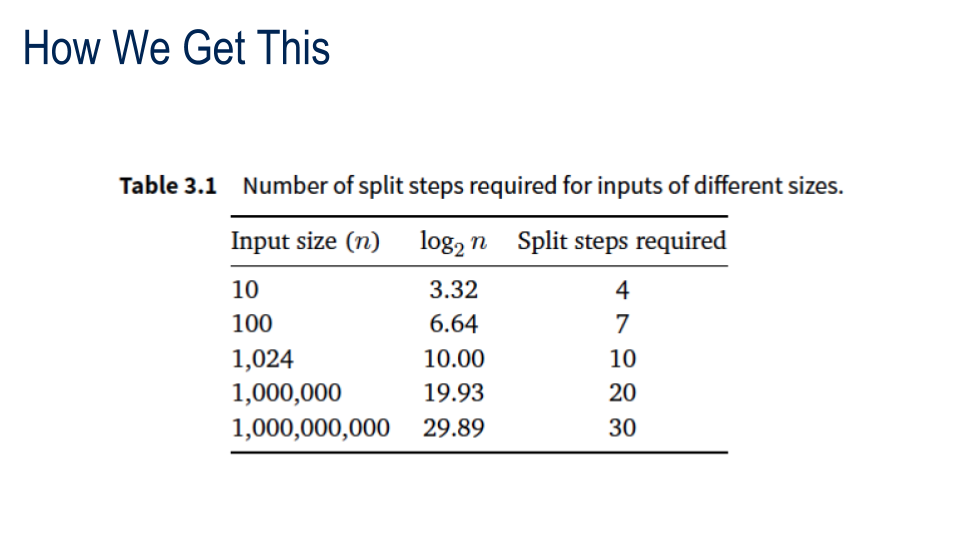
Think powers of 2 - the number of steps is the power of two that's closest to N.
This reminds us of binary numbers: the number of splits is the number of binary digits needed to represent N
Introducing Logarithms

Introducing Logarithms
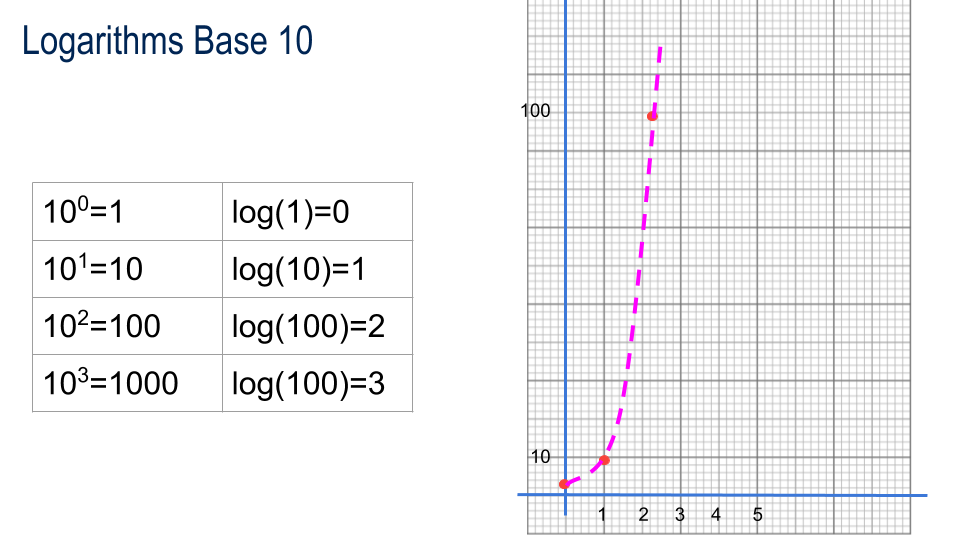
| 100=1 | log(1)=0 |
| 101=10 | log(10)=1 |
| 102=100 | log(100)=2 |
| 103=1000 | log(1000)=3 |
logarithms base 10
Introducing Logarithms

Introducing Logarithms
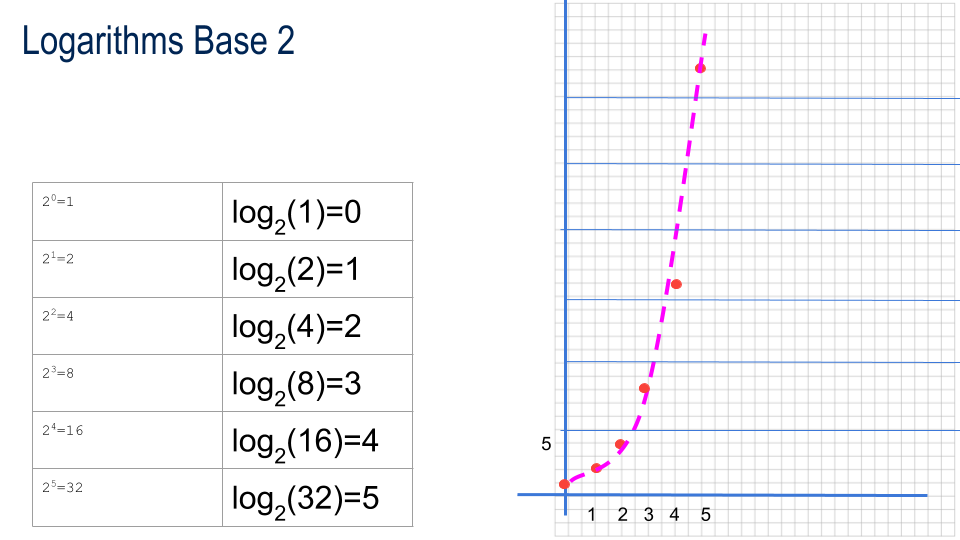
| 20=1 | log(1)=0 |
| 21=2 | log(2)=1 |
| 22=4 | log(4)=2 |
| 23=8 | log(8)=3 |
logarithms base 2
Find a Word in a Dictionary with N words
STOP+THINK: For how long can this go on?
N > N/2 > N/4 > N/8 > ... 1 and DONE
Think powers of 2 - the number of steps is the power of two that's closest to N.
This reminds us of binary numbers: the number of splits is the number of binary digits needed to represent N
Find a Word in a Dictionary with n pages
STOP+THINK: For how long can this go on?
Binary Search is a simple iteration
in which we cut the search space in
half with each iteration
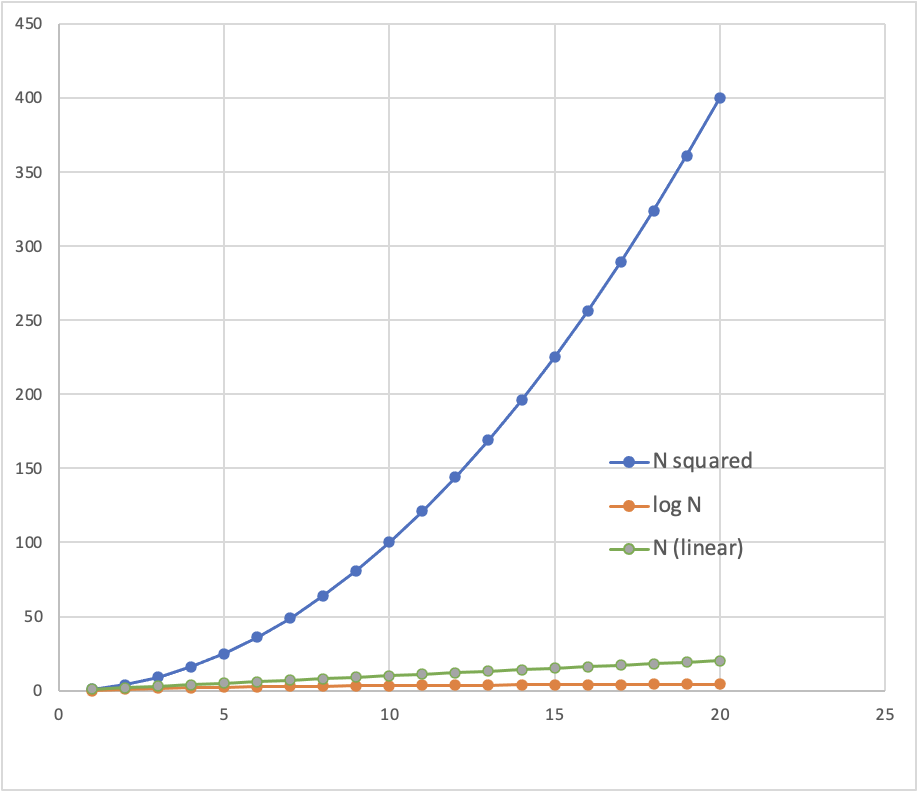
Complexity Take Away: Some tasks are LOGARITHMIC - the number of steps grows as the logarithm of the number of cases.
WE LIKE THIS.
number of objects/cases/datapoints
time
Scenario: classroom Valentines day
five children
each child sends 4 cards
total 20 cards
8 children
each child sends 7 cards
total 56 cards
STOP+THINK: If everyone in OUR class (N=126) sent a Valentine to everyone else in the class, how many cards would be sent?
Merge Sort
Consider a classroom with two groups of children lined up in order of height.
We want them to form one line, also arranged by height.
What's Happening Here?
What's Happening Here?
What's Happening Here?
What's Happening Here?
What's Happening Here?
What's Happening Here?
What's Happening Here?
What's Happening Here?
What's Happening Here?
What's Happening Here?
Merge Sort
Start with a pile of data to be sorted
Repeatedly divide the pile in half until you get to singletons
Repeatedly merge the results.
2
1
7
5
2
1
7
5
2
1
7
5
2
1
7
5
2
5
1
7
split
split
split
merge
merge
merge
2
1
7
5
2
1
7
5
2
1
7
5
5
2
7
1
merge #1, 4 operations
merge #2, 4 operations
N= 4
2
1
7
5
2
1
7
5
2
1
7
5
split
2
1
7
5
2
1
7
5
2
1
7
5
2
1
7
5
split
2
1
7
5
2
1
7
5
2
1
7
5
2
1
7
5
merge
2
1
7
5
2
1
7
5
2
1
7
5
2
1
7
5
merge
2
1
7
5
2
1
7
5
2
1
7
5
2
1
7
5
merge
2
1
7
5
2
1
7
5
2
1
7
5
2
1
7
5
2
1
7
5
merge
2
1
7
5
2
1
7
5
2
1
7
5
2
1
7
5
2
1
7
5
merge
2
1
7
5
2
1
7
5
2
1
7
5
2
1
7
5
2
1
7
5
merge
2
1
7
5
2
1
7
5
2
1
7
5
2
1
7
5
2
1
7
5
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
3
5
6
7
8
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
5
10
4
6
7
8
9
1
2
5
3
10
7
8
4
6
9
1
2
4
9
3
5
6
7
8
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
5
10
4
6
7
8
9
1
2
5
3
10
7
8
4
6
9
1
2
4
9
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
STOP+THINK: How many split steps?
# merges depends on log2 N
O(N log2 N)
number of objects/cases/datapoints
time
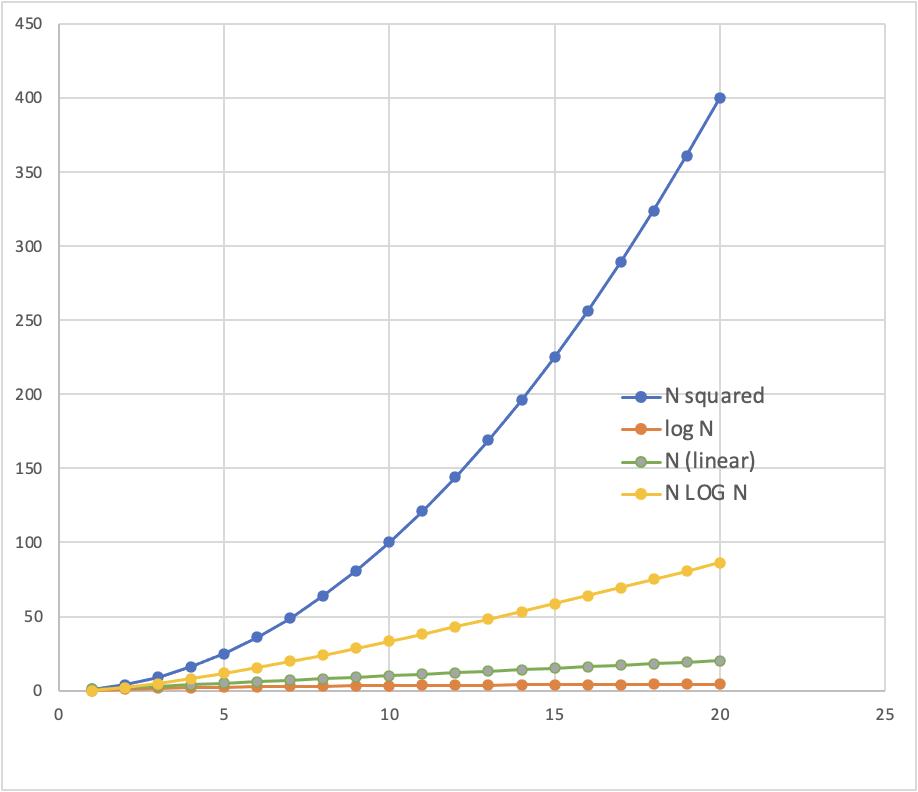
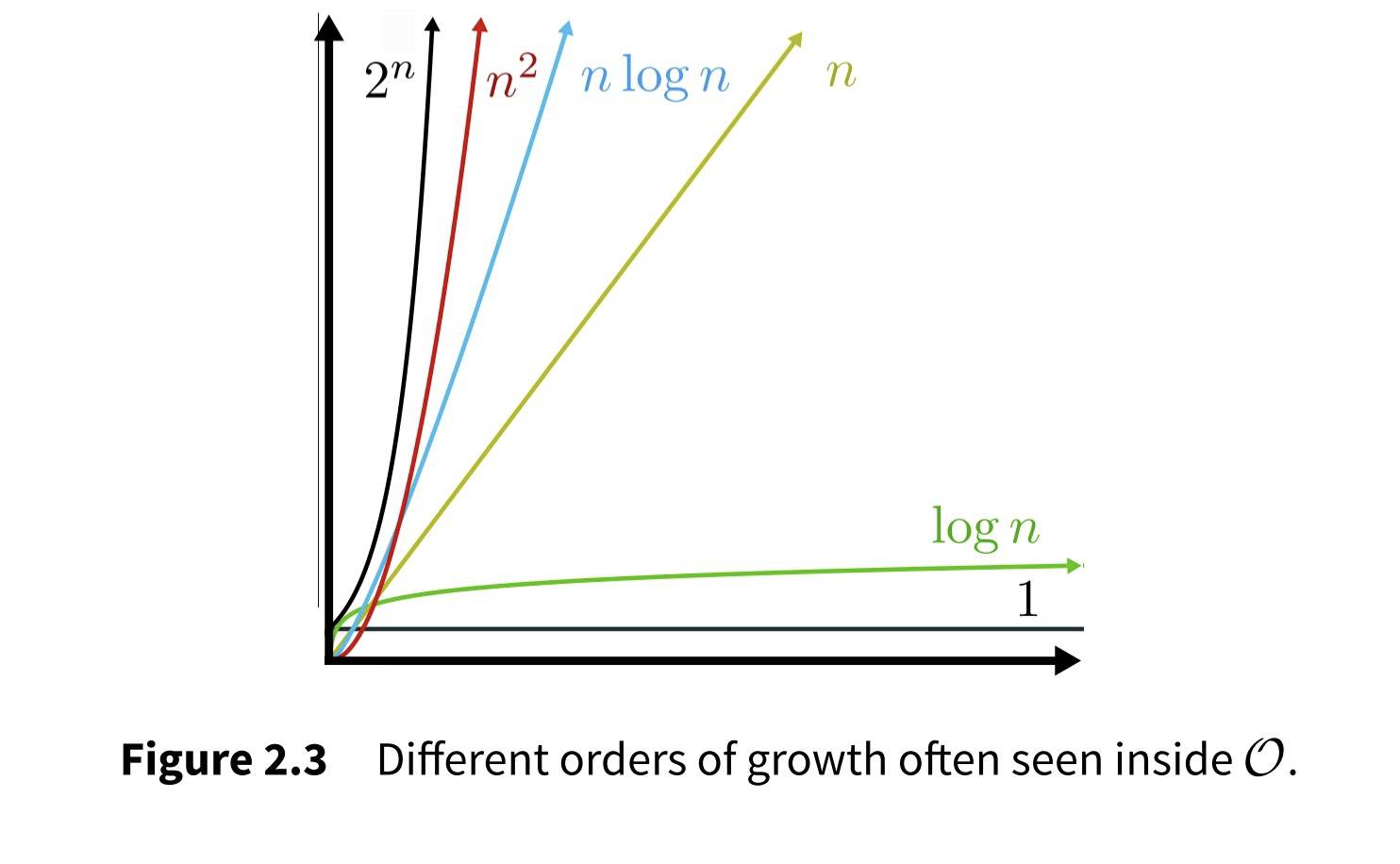
"constant" time
"linear" time
"exponential" time
"quadratic" time

Next
Recursion



Fn = Fn-1 + Fn-2
F1 = 1
F2 = 1

Fibonacci Numbers
Backtracking in a Maze
If I take a fork in the road while traversing a solution space how can I go back when I hit a dead end?
Backtracking
Solve This Maze
F
FLRB
Solve This Maze
F
F
F
FLRB
Solve This Maze
F
L
F
F
FLRB
Solve This Maze
F
R
L
F
F
FLRB
Solve This Maze
F
R
L
F
F
L
FLRB
Solve This Maze
F
F
R
L
F
F
L
FLRB
Solve This Maze
F
F
R
L
F
F
L
L
B
FLRB
Solve This Maze
F
F
R
L
F
F
L
B
B
FLRB
Solve This Maze
F
F
R
L
F
F
L
B
B
FLRB
Solve This Maze
F
R
L
F
F
B
B
B
B
FLRB
Solve This Maze
F
R
L
F
F
B
B
B
B
FLRB
Solve This Maze
F
R
F
F
B
B
B
B
B
FLRB
Solve This Maze
F
R
F
F
B
B
B
B
B
FLRB
Solve This Maze
F
R
F
F
L
F
B
B
B
B
B
FLRB
Solve This Maze
F
R
F
F
L
F
B
B
B
B
B
FLRB
Solve This Maze
F
R
F
F
L
F
F
L
B
B
B
B
B
FLRB
Solve This Maze
F
R
F
F
L
F
F
L
F
F
F
B
B
B
B
B
FLRB
Solve This Maze
F
R
F
F
L
F
F
L
F
F
F
B
B
B
B
B
FLRB
Solve This Maze
F
R
F
F
L
F
F
L
F
F
F
R
F
R
B
B
B
B
B
B
FLRB
Solve This Maze
F
R
F
F
L
F
F
L
F
F
F
R
F
R
B
B
B
B
B
B
FLRB
Solve This Maze
F
R
F
F
B
L
F
F
L
R
B
B
B
B
B
B
F
B
B
B
B
FLRB
Solve This Maze
B
F
B
R
F
F
B
B
B
L
F
F
L
R
B
B
B
B
B
B
F
B
FLRB
Solve This Maze
F
R
F
F
L
F
F
R
B
B
B
B
L
B
B
B
B
B
B
B
B
B
B
FLRB
Solve This Maze
F
R
F
F
L
F
F
R
L
F
F
F
F
B
B
B
B
B
B
B
B
B
B
B
B
B
B
FLRB
DECISION POINTS

R, L, or S
L or S
R or S
R or L
Solve This Maze

R, L, or S
L or S
R or S
R or L
Solve This Maze

R, L, or S
L or S
R or S
R or L
Solve This Maze

L
R
How many paths?

L
R
3
2
2
2
2
2
2
3
3x2x2x2x2x
How many paths?

3
2
3
2
2
2
2
2
Further Reading
Tutorial
Packing up after a burglarly
The Sierpinski Triangle
Supplementary
Tutorial
How to Draw a Tree
Ask students to take 30 seconds to sketch a tree. Like a tree in a forest. Comment how many folks do this by drawing smaller and smaller branches. Then suggest an algorithmic approach that's iterative: draw 1 thick trunk; draw two slightly narrower branches off it; draw two still narrower branches off each of these and so on.
for i = 1 to 5 draw i "branches" off of each previous branch
Point out that trees have a cool quality - each set of branches looks like a tree. A tree can be thought of as a trunk out of which grow two trees. And each of those trees is a branch out of which grows two trees, etc. all the way out to the leaves. This is the basic idea of recursion - a problem that can be solved by repeatedly solving smaller versions of itself.
Write simple tree code on board (see slide ?). Follow the code step by step. when you get to tree(n-1) write a reminder over on the left "was at step 5 of tree(5)" and then re-enter code for n=4. Draw branch, get ready to recursively call tree(3), write the reminder over on the "stack" and re-enter for tree(3). Continue through tree(2), tree(1), tree(0). Tree(0) is just drawing a leaf and then we are done. We go back to where we were - effectively popping off the recursion stack - and do the second (right) tree(1) branch. Then we go down to tree(0) and draw leaves. And then we pop tree(2) off the stack and draw the right hand tree (2) branch. Then we push a reminder of where we are in tree(2) and go to tree (1), etc.
Don't use "push" "pop" and "stack" while doing this but after we get used to it ask what this looks like, this list where the bottom (a reminder that we were doing tree(5)) is the first thing we noted but the last thing we will return to. Answer: FILO - it's a stack. In fact we call it the recursion stack or the call stack.
Tutorial
Human Recursion - Fibonacci
Introduce Fibonacci sequence. Write pseudocode for recursive algorithm. Tell students they will each BE the algorithm. Ask one student "what's F(4)?" and have them walk through the algorithm. When it gets to F(3)+F(2) they have to ask two classmates to supply the result and wait for them: "Senya, what is F(3)? Rudolph, what is F(2)?" Rudolph can answer "1" but Senya has to ask two other classmates: "Paul, what is F(2)? Ren, what is F(1)?" Paul says 1 and Ren says 1 and then Senya can report back "2." And now the first student can add these together and announce that F(4) is 3. Repeat a few times. Eventually point out how many separate calls to the code we have (2x2x2 etc.). And that there was repetition (e.g., F(6) involves F(5) and F(4) but F(5) also involves F(4). Suggest that we could save time if we wrote results down, say, in an array called fibmemo, when we computed them the first time. And we can adjust the code to take account of this.
fib(n) if fibmemo[n] not null, return fibmemo[n] if n<3 return 1 fibmemo[n] = fib(n-1)+fib(n-2) return fibmemo[n]
Mention that this is called "memoization" and we can use it whenever we have an algorithm that might involve calculating the same thing repeatedly and that this can save lots of time.
Tutorial
In Person Merge Sort
Review the "fish sorting" merge algorithm and ask what was special about it - namely that it is linear (O(N)) in the number of items to be merged. Then ask about bubble sort and what we learned about it. Review the algorithm itself - line up items, scan left to right comparing and swapping, repeat but only to the last item but one, etc. Note how this gives us a "triangle" of activity (vs the square of visiting every space on a chessboard) but it's still O(n2).
Now we will see if we can come up with a recursion like approach to sorting a deck of cards.
First we just demo it. Take a deck of cards, split it in half, split it in half again. And again and again until we reach single cards. Then I announce that a single card is basically a sorted list and so I can take each of the last splits and merge them one by one. When I've done this first ordering merge I'll have "touched" every card once.
Now I have a bunch of sorted pairs of cards. Once again I reverse the split and merge pairs in to sorted piles of 4. And so on all the way back to the top. I remind folks that each time we did the merge we touched all the cards once.
And then I ask how many split steps there were and how many merge steps. Of course it's the same, but how many? Let's think about what goes on when I do splits of 16 cards getting down to single cards. 16 -> 2 piles of 8 -> 4 piles of 4 -> 8 piles of 2 -> 16 singles. Four splitting steps. Anyone see a pattern? How about 23? -> 11 + 12 -> 6+5 + 6+6 -> 3+3+3+2+3+3+3+3 -> 2+1+ 2+1+2+1+2+2+1+2+1+2+1+2+1 -> 1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1. Five splits.
INSIGHT: the number of splits it takes to get to single cards is related to powers of two. In fact, it's the log base two of the number of cards, rounded up.
Now let's try it ourselves. Tell students that they are all going to be this algorithm.
1 sort(cards) 2 if cards.Count = 1 return cards 3 [firstHalf,secondHalf] = split(cards) 4 firstHalf=sort(firstHalf) 5 secondHalf=sort(secondHalf) 6 return merge(firstHalf,secondHalf)
Give the full, unsorted deck to one student. Tell them to "follow the algorithm." When they get to line 4 have them pass the half to another student saying "sort these" and at line 5 hand the other half to another student. Remind people to remember who they received cards from. Keep this up until people start receiving single cards. At this point we remind them that the pseudocode tells us what to do - namely they should hand the card back to the person who gave it to them. Then we aks that person what they now do with the two cards they got back. Answer: merge them. For the first person with just two cards this just means "put the smaller card on top." Remind them that they are now executing step 6 and that they should now return this merged pile to the person from whom they got cards to begin with. The recipient now executes their own line 6 and merges what they received and passes the result back up the line. Eventually the first person receives two half decks and merges these to form the finished sort.
Ask students how many merge "touches" were happening at each step? Make sure they can see how we add up what everyone was doing in parallel and that there were a total of N merge touches. And then review the question of how many of these steps there were - and we come back to log N.
Tutorial
In Person Merge Sort (continued)
1 sort(cards)
2 if cards.Count = 1 return cards 3 [firstHalf,secondHalf] = split(cards) 4 firstHalf=sort(firstHalf) 5 secondHalf=sort(secondHalf) 6 return merge(firstHalf,secondHalf)
So, here we have discovered a sorting algorithm that does "better" than bubble sort. How many operations overall do we have here? At each step we have N "merge touches" and we have log N steps so we multiply these together to get NlogN. Since we know that log N is always less (and mostly much less) than N, we know that N log N gets more and more less than N squared as N gets bigger.
TAKEAWAY
We've seen how to use recursion in a practical problem. We've seen how to methodically count the steps so that we can compute the "complexity" of an algorithm in terms of the number of cases (N) that it has to process. And we've seen how one level of comparison compares to another (N log N < N squared).
Let's think for minute about our tree drawing algorithm. How many steps were involved there? When we wanted to draw a 5 level tree we started with 1 and then we drew two branches. And off of each of these we drew two branches. And on and on and on.
total drawings = 1 + 2 + 4 + 8 + 16 + 32
As the tree gets larger the number of drawings increases like two to the N. This is far more intense that just N squared!
Tutorial
In Person Merge Sort (continued)
How much difference would this make in practice? Let's imagine you are the machine again. And this time you have to say, silently, the word "Mississippi" for each operation. When you are done you can say (out loud) DONE.
Assign a student to be a linear algorithm, one to be NlogN, one to be N2 and one to be 2N.
Remind the NlogN person to round.
First number is N=3.
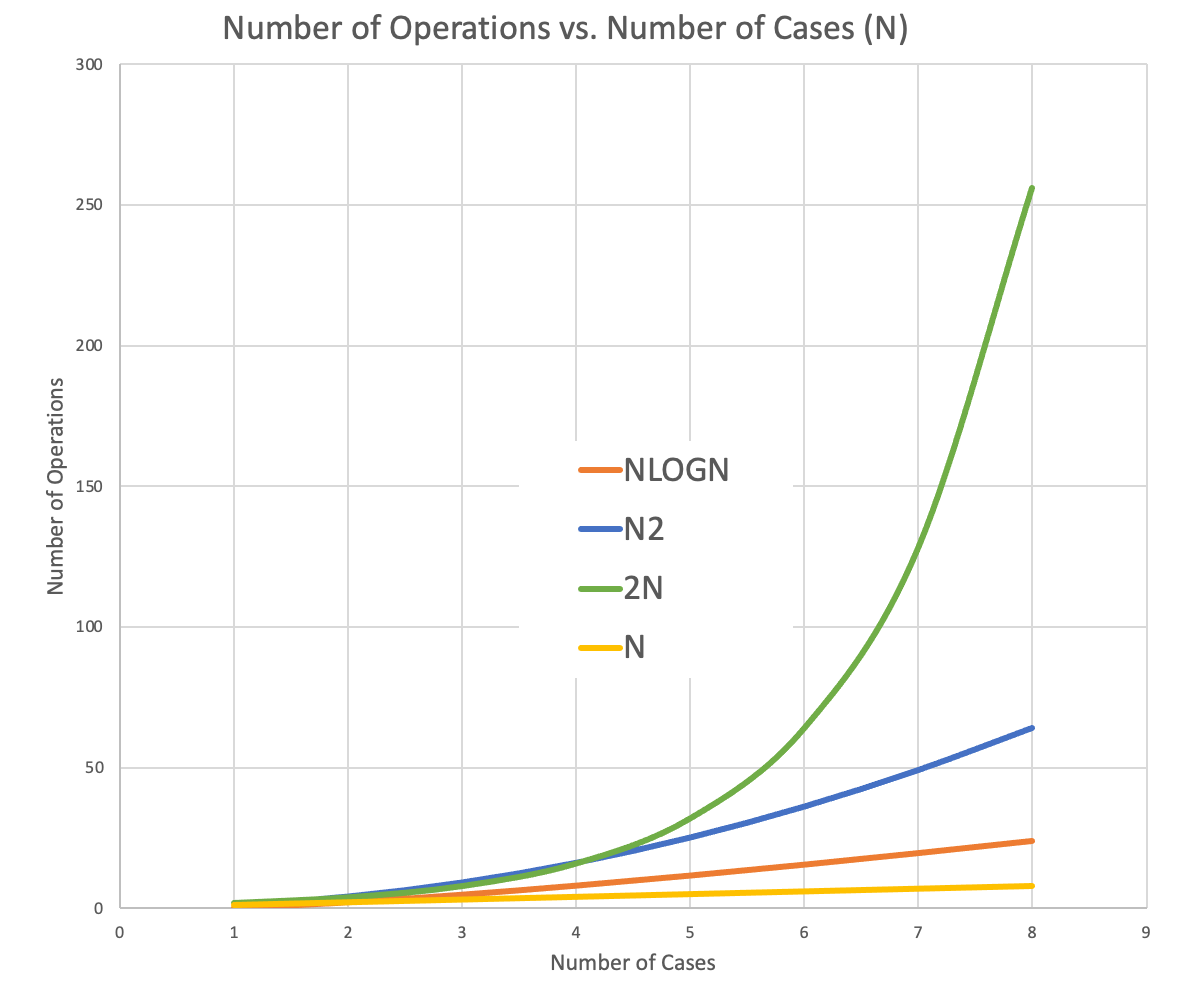
2N
N2
Nlog N
N
| N | N log N | N2 | 2N |
|---|---|---|---|
| Mississippi Mississippi Mississippi |
Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi |
Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi |
Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi |
Text
Tutorial
In Person Merge Sort (continued)
How about N=6? We wait while it takes 2N over a minute before saying "done" where as NlogN got to done in about 15 seconds.
Finish by recommending a re-read of chapter 2 in Filho - Complexity - in light of what we have seen in chapter 3 - Strategy, namely, that there are different techniques for harnessing the power of repetition and that as problem solvers we need to be mindful of two things: how we might apply a given repetition strategy to a given problem (aware that (1) it's not always straightforward, and (2) that one technique might be more or less appropriate than another for a given problem), and how how long a given solution will take is related to the number of cases we want to deal with.
Hopefully someone will ask about a practical application of all of this. One that might get folks thinking is how long it takes to train a machine learning model. Suppose we train a model on a million training examples but we find the system does not perform as well as we hope. And so we decide to move on to a new corpus (body) of training data that has a billion examples (one billion = 1000 millions). If we have a 2N algorithm it will take, basically, forever. If it's linear it will take 1000 times as long. At N2 a million times as long. But beyond that it gets simply "intractable"

2N
N2
Nlog N
N
| N | N log N | N2 | 2N | |
|---|---|---|---|---|
| Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi |
Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi |
Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi |
Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi |
Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi Mississippi |
Tutorial
Is there a limit to what is possible?
The chart to the right shows that the plot of 2 to the N completely dominates the picture, far above polynomial line (this is what we call N to the power of - N squared is just the first case of this) - even here showing how N to the 30th power and N 50th power are practically flat compared to when N is in the exponent.
There's a big space between where the polynomial lines are and where the exponential lines are in this plot. We think of the stuff down in the polynomial zone as do-able or tractable while the stuff above this zone is not so tractable.
For more on this, learn about complexity and P vs NP on the web, perhaps starting with these two video lectures/tutorials:
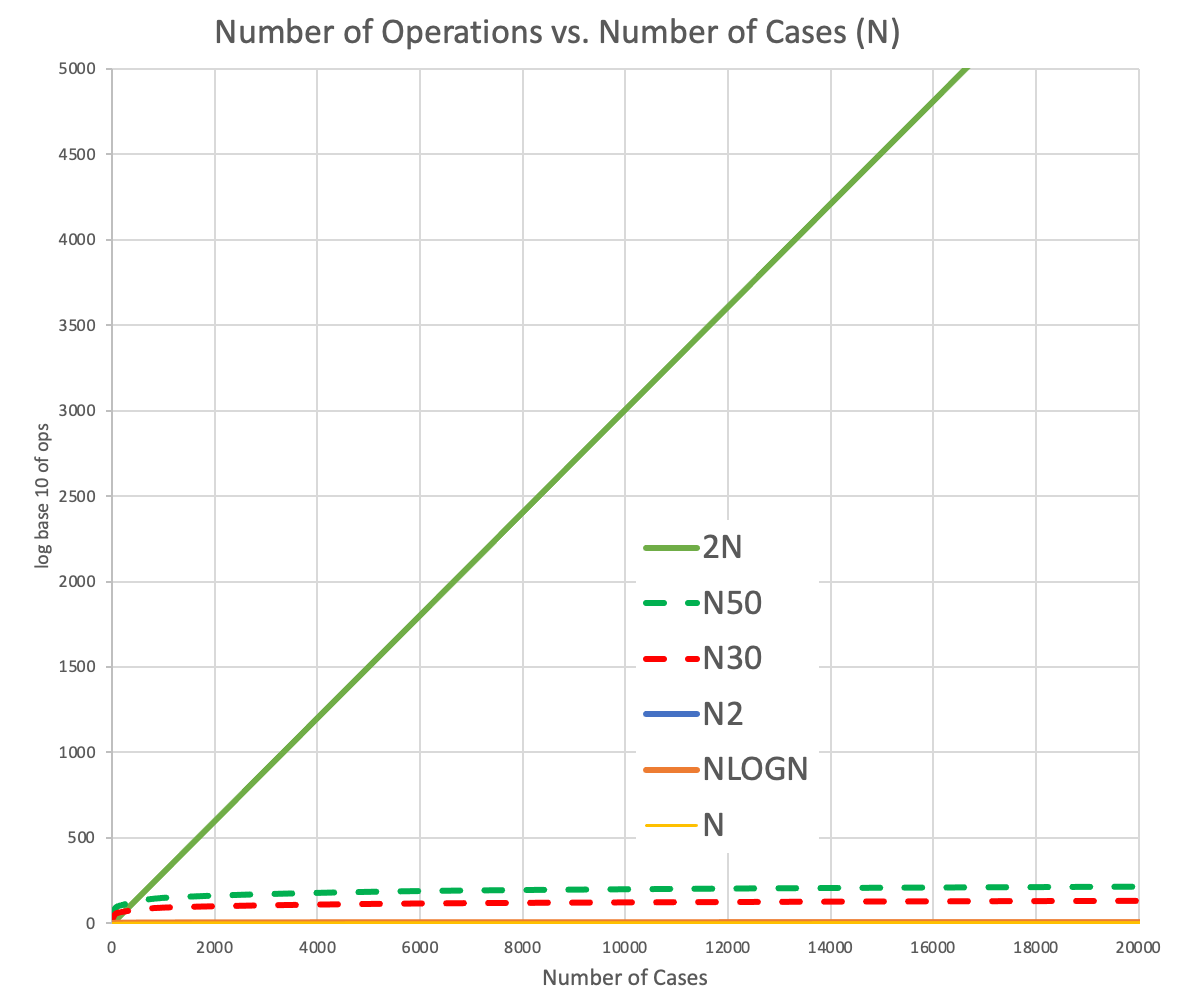
2N
N50
N30
N2
Nlog N
N
How to Draw a Tree
Filling a Backpack
Filho Example

The "solution space" is all the possible combinations of items. The power set. The truth table.

How can we use repetition to search this solution space for best combination?
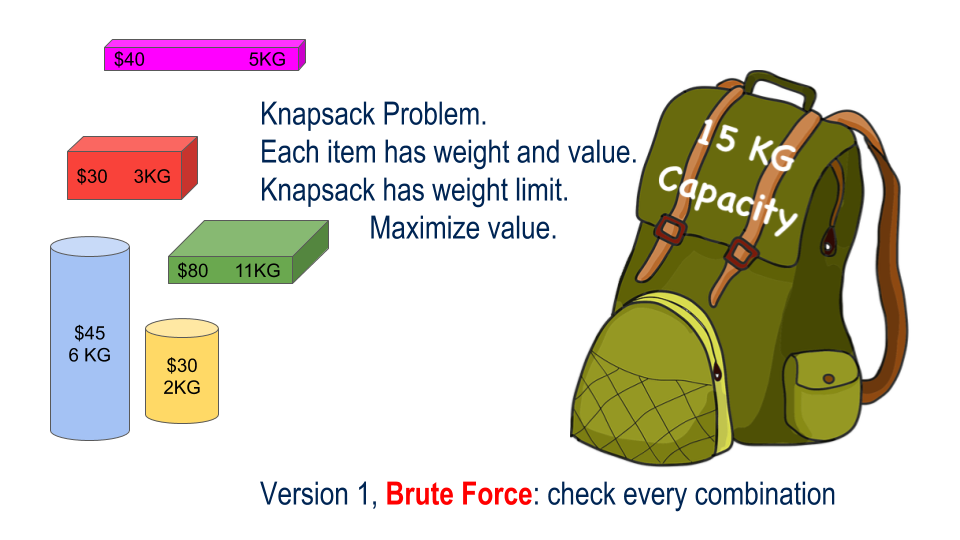
Option 1: Brute Force
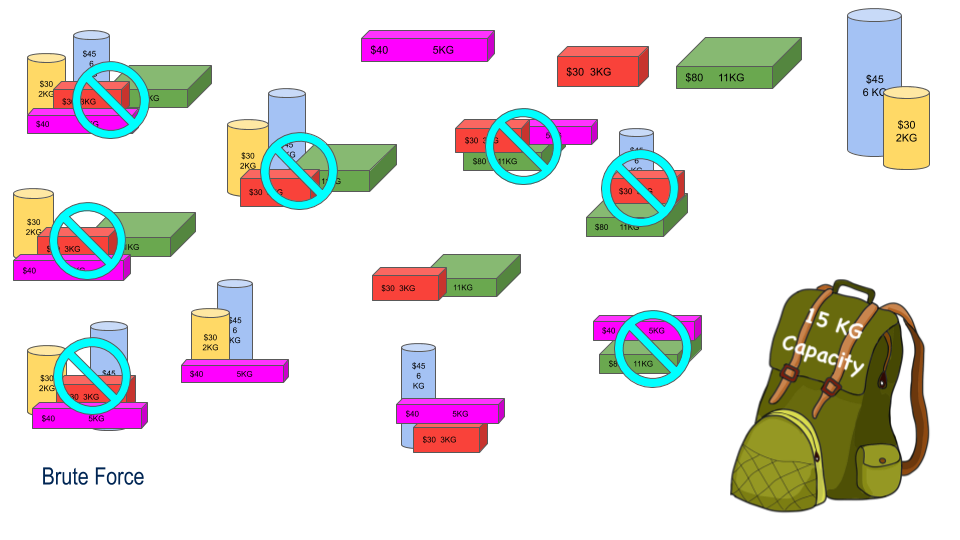
Some Combinations Too Heavy
maxRev([items],capacity) recursion
mR( , 15 )
30
2
45
6
30
3
80
11
40
5
mR( , 13 ) + 30
mR( , 15 )
mR( , 15 )
mR( , 9 ) + 45
30
2
45
6
30
3
80
11
40
5
30
3
80
11
40
5
30
3
80
11
40
5
30
3
80
11
40
5
30
3
80
11
40
5
45
6
30
3
80
11
40
5
mR( , 7 ) + 30 + 45
mR( , 9 ) + 30
mR( , 15 )
80
11
40
5
mR( , 12 ) + 30
80
11
40
5
mR( , 9 ) + 45
80
11
40
5
mR( , 6 ) + 45 + 30
80
11
40
5
80
11
40
5
mR( , 9 ) + 30
80
11
40
5
mR( , 6 )+ 30 + 30
80
11
40
5
mR( , 7 ) + 30 + 45
80
11
40
5
mR( , 7 ) + 30 + 45+ 30
mR( , 15 )
40
5
mR( , 12 ) + 30
80
11
40
5
mR( , 4 ) + 80
40
5
mR( , 12 ) + 30
80
11
40
5
mR( ,1 ) + 30 + 80
40
5
mR( , 12 ) + 30
40
5
mR( , 9 ) + 45
40
5
mR( , 6 ) + 45 + 30
40
5
40
5
mR( , 9 ) + 30
40
5
mR( , 6 )+ 30 + 30
40
5
mR( , 7 ) + 30 + 45
40
5
mR( , 7 ) + 30 + 45+ 30
maxRev([items],capacity) recursion
30
2
45
6
30
3
80
11
40
5
30
2
45
6
30
3
80
11
40
5
mR( , 15 )
40
5
mR( , 4 ) + 80
40
5
mR( ,1 ) + 30 + 80
40
5
mR( , 12 ) + 30
40
5
mR( , 9 ) + 45
40
5
mR( , 6 ) + 45 + 30
40
5
40
5
mR( , 9 ) + 30
40
5
mR( , 6 )+ 30 + 30
40
5
mR( , 7 ) + 30 + 45
30
2
45
6
30
3
80
11
40
5
30
2
45
6
30
3
80
11
40
5
30
2
45
6
30
3
80
11
40
5
30
2
45
6
30
3
80
11
40
5
30
2
45
6
30
3
80
11
40
5
30
2
45
6
30
3
80
11
40
5
30
2
45
6
30
3
80
11
40
5
30
2
45
6
30
3
80
11
40
5
30
2
45
6
30
3
80
11
40
5
30
2
45
6
30
3
80
11
40
5
30
2
45
6
30
3
80
11
40
5
30
2
45
6
30
3
80
11
40
5
30
2
45
6
30
3
80
11
40
5
Filho Example

STOP+THINK: Elaborate the brute force solution.
Filho Example

STOP+THINK: Write the brute force solution in pseudocode.
for each item create a knapsack with the item and a knapsack without the item and then compare all the possible knapsack combinations.
See Also
Problem Solutions
Finis
Outtakes
SOLUTION SPACES
POINT 1:
Suppose I am making soup and I want to add the right amount of salt, pepper, and curry. What is the best combination?

The solution will be three numbers - an amount of salt, an amount of pepper, and an amount of curry.
We can represent this as (Sright, Pright, Cright).
Suppose I am making soup and I want to add the right amount of salt, pepper, and curry. What is the best combination?
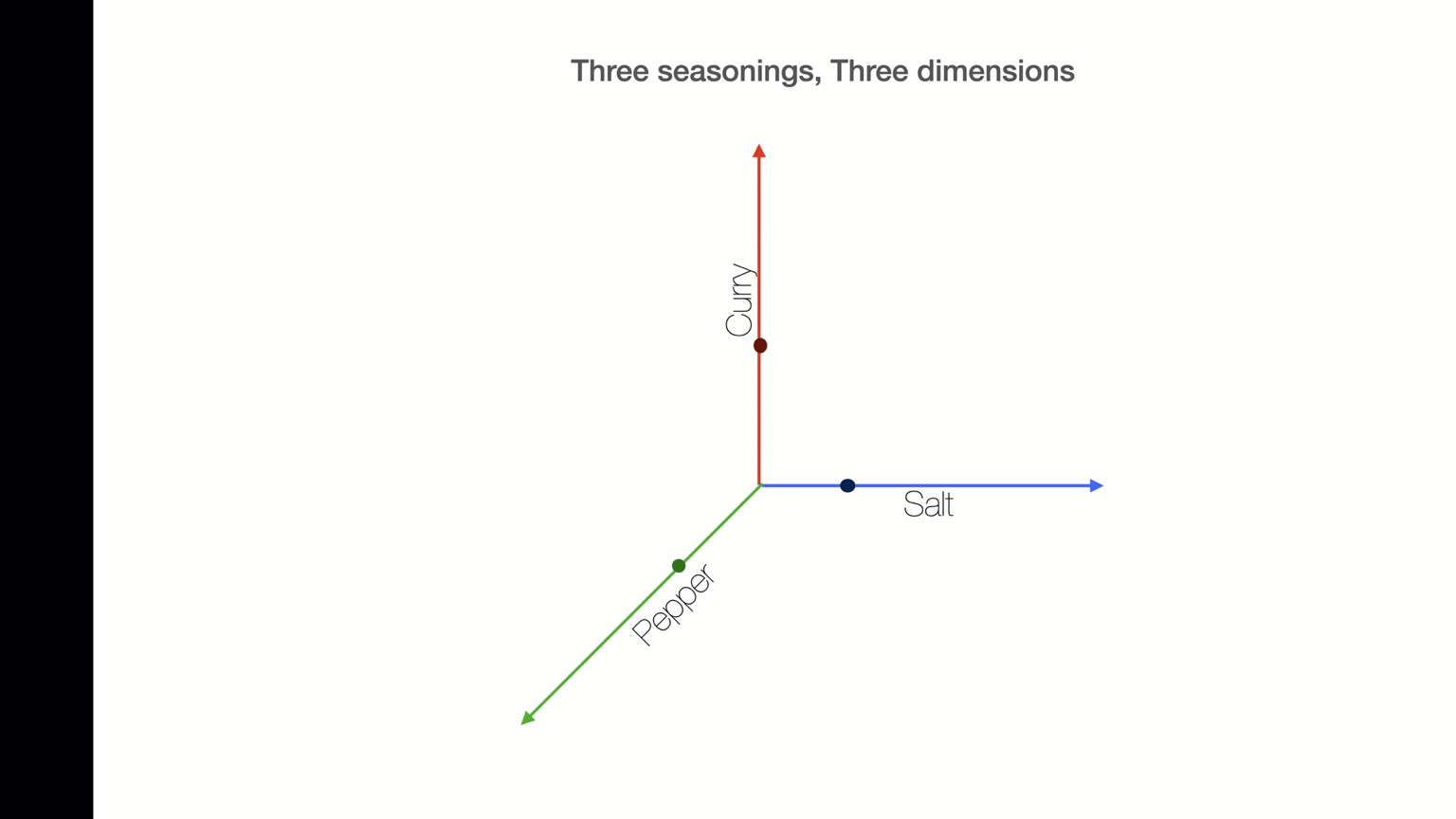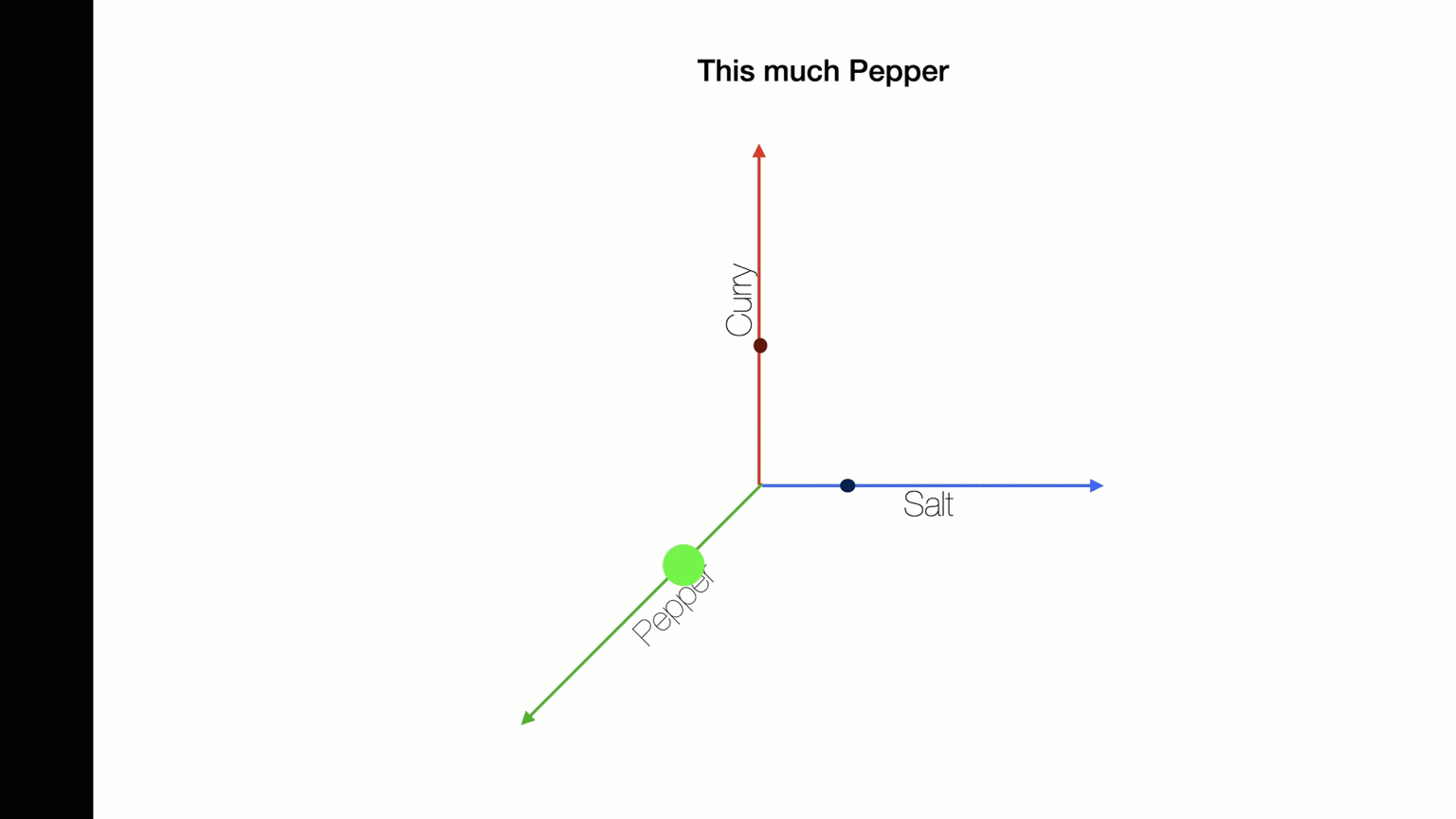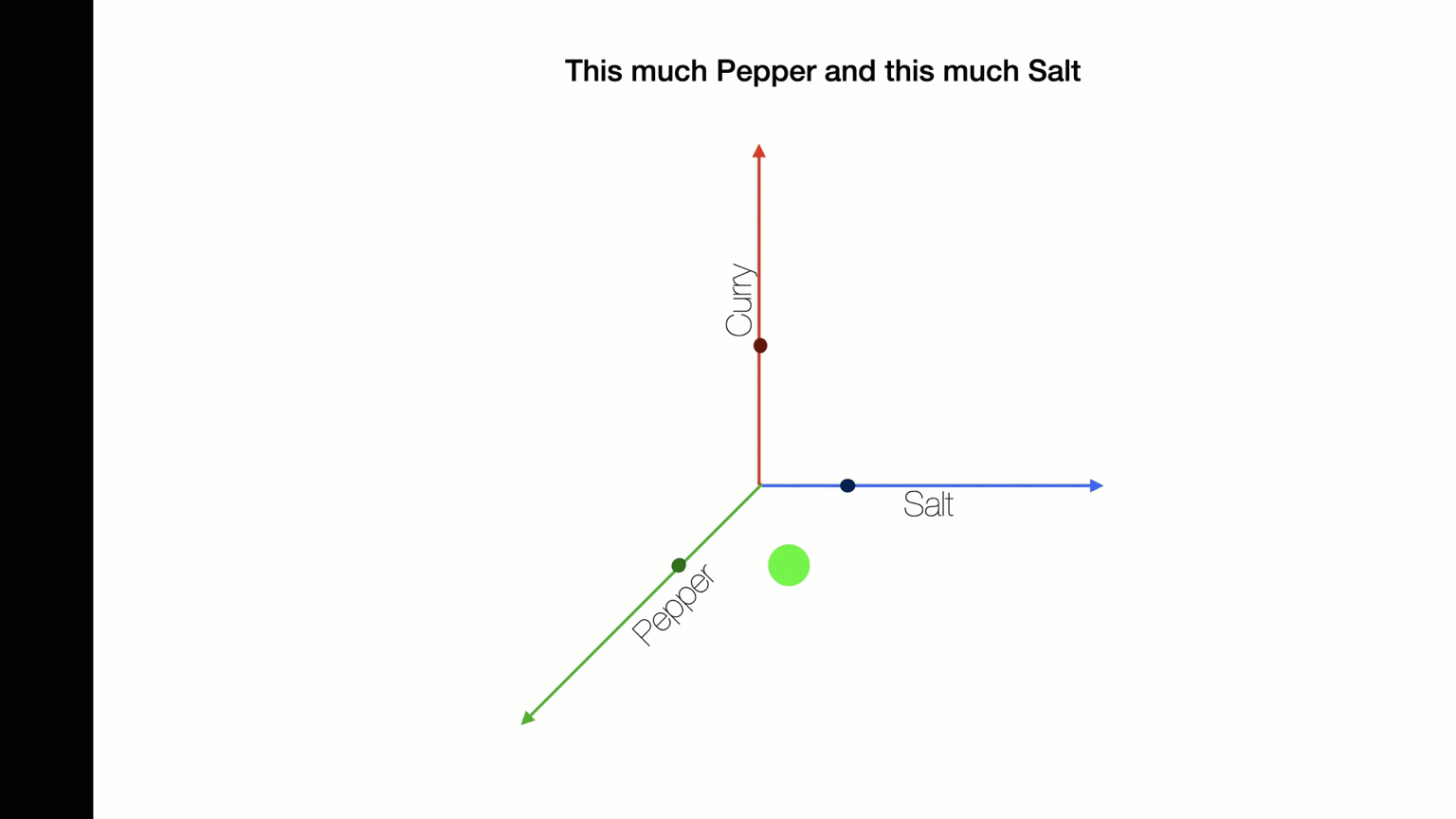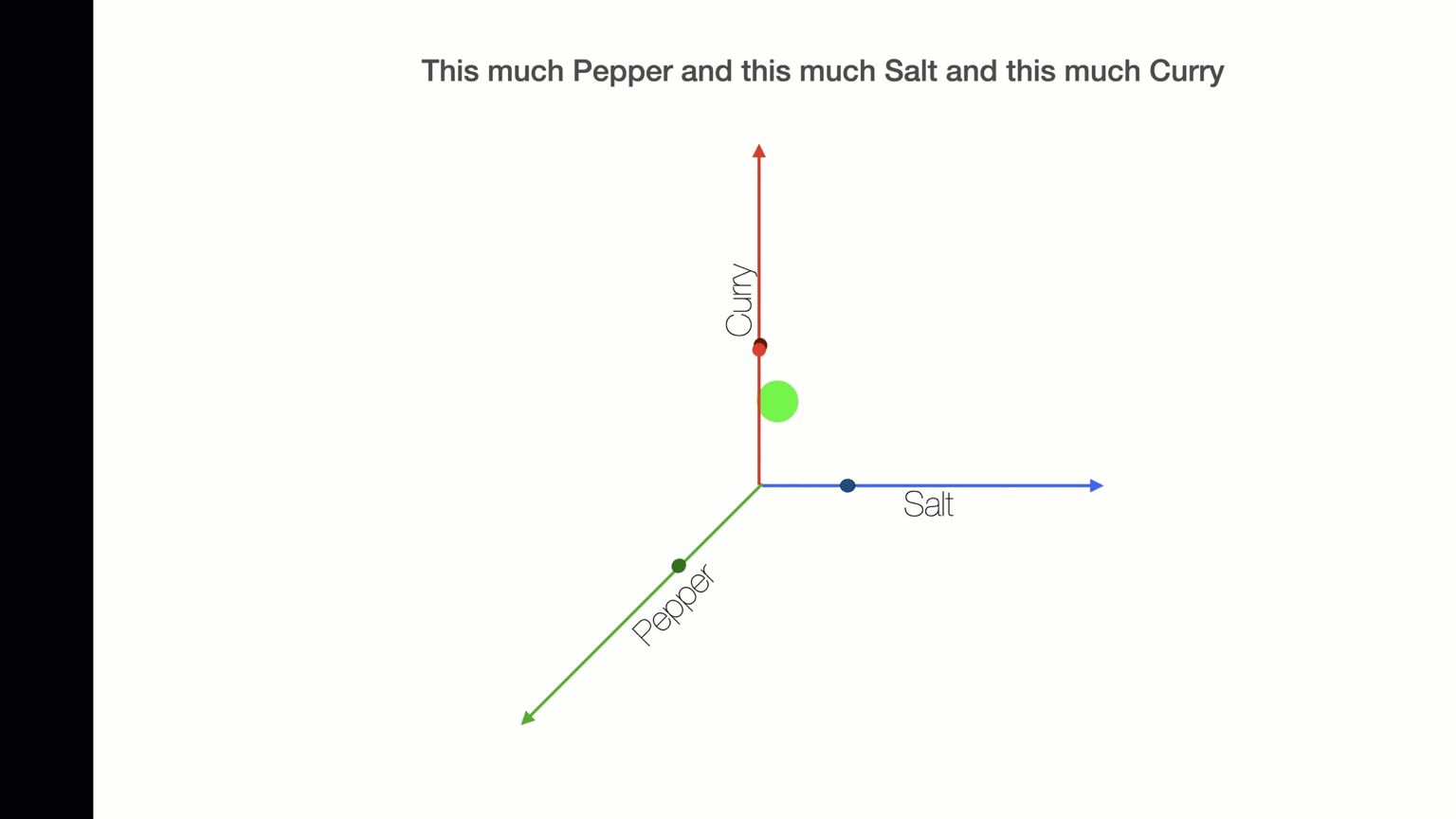
Suppose I am making soup and I want to add the right amount of salt, pepper, and curry. What is the best combination?
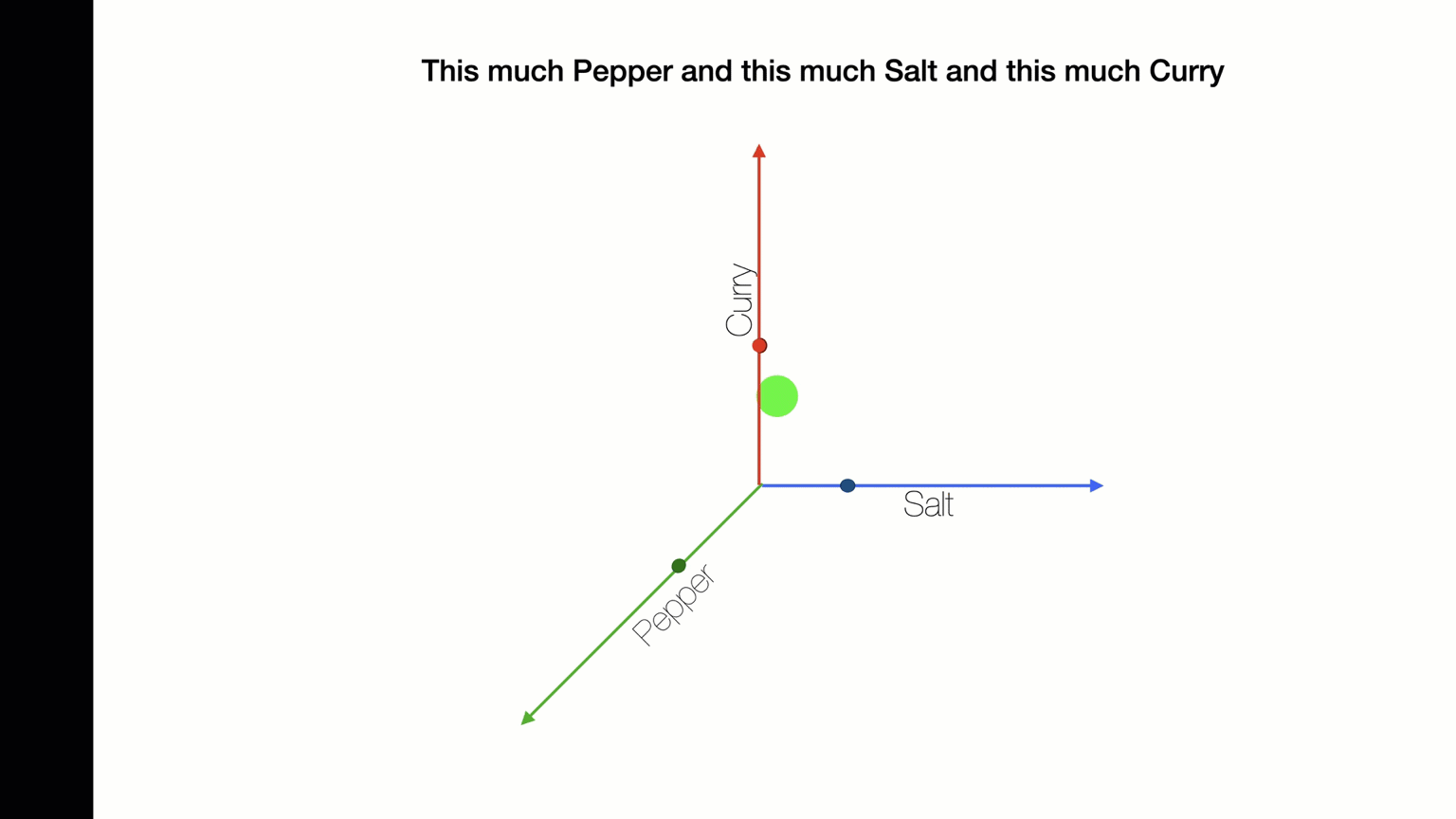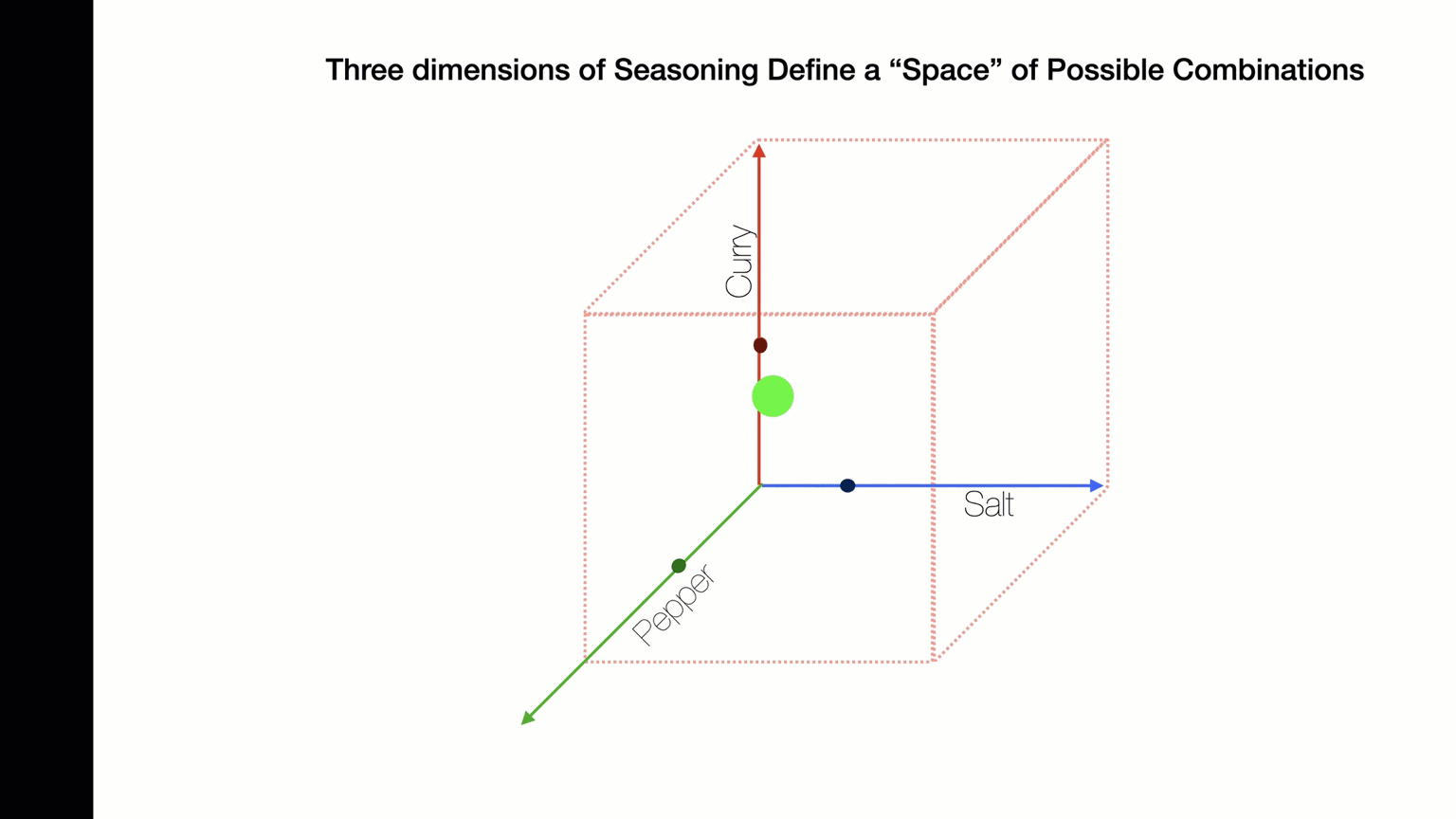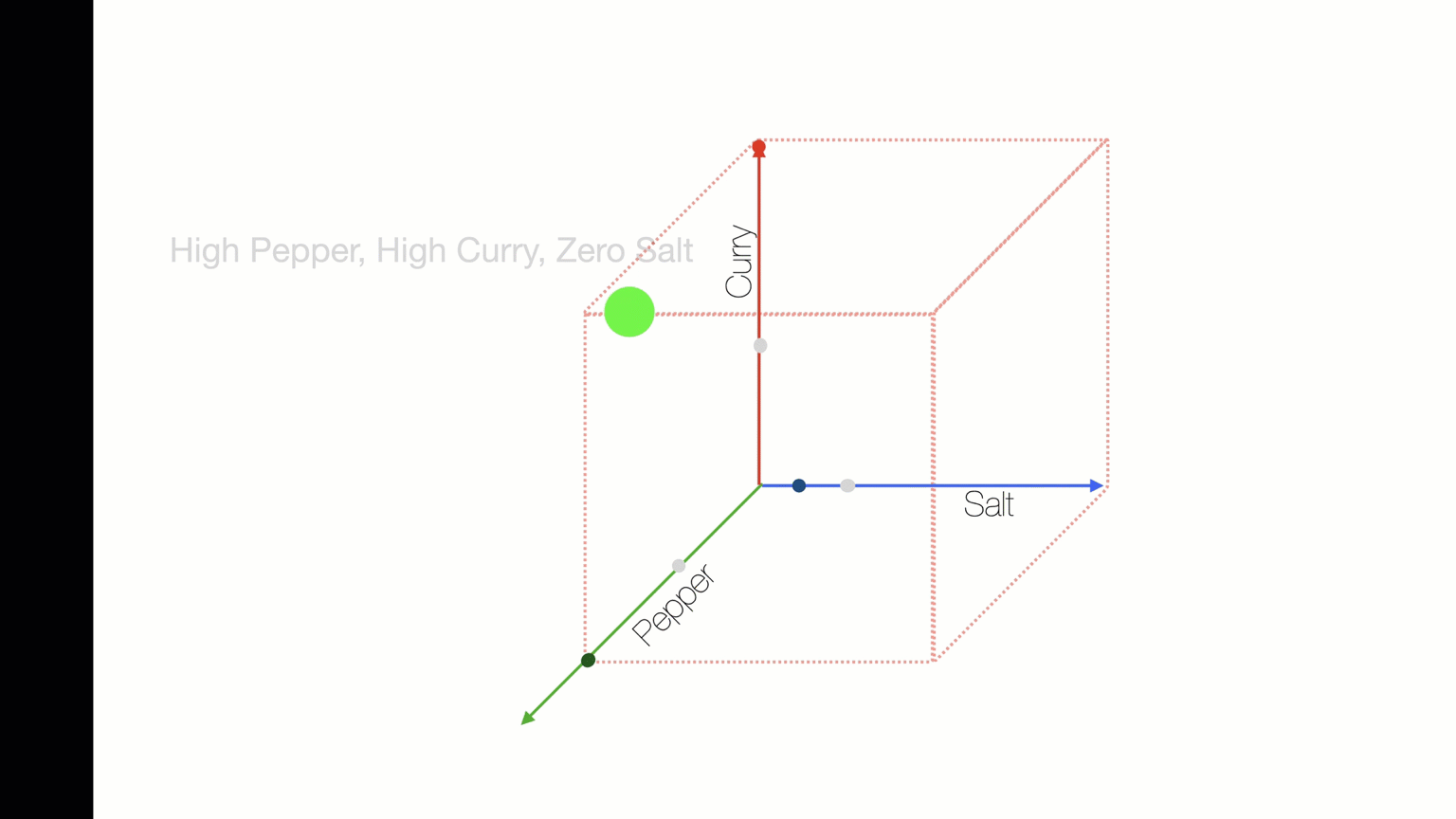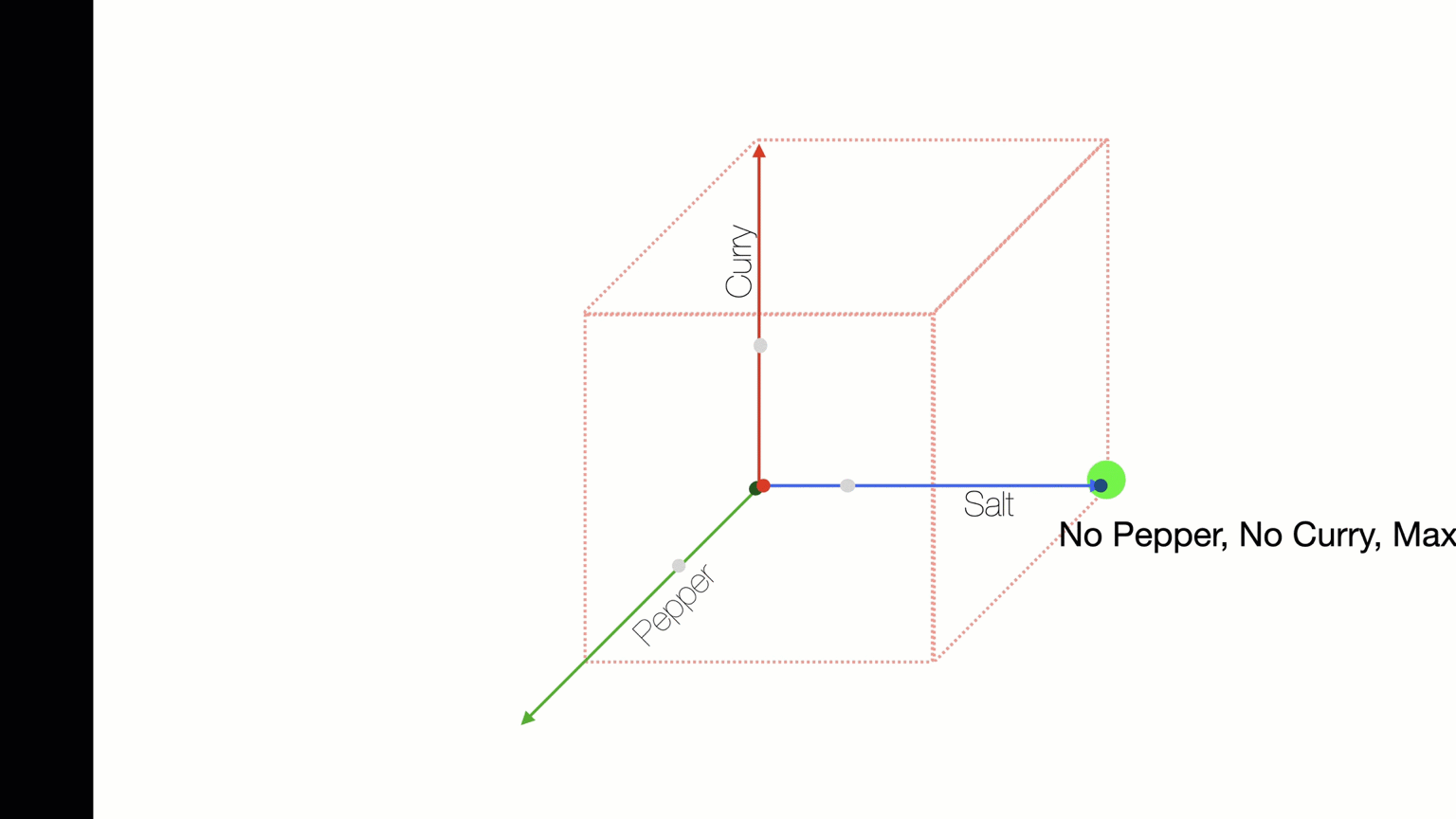
PROBLEM SOLVING AS TRAVERSING SOLUTION SPACES
LOOKING FOR WHAT?
POINT 2:
Biggest Reward
Smallest Error
First Satisfactory Result
LOOKING FOR WHAT?
POINT 2:
Staring at a Brick Wall
Next Time: Pattern Recognition
OR

Recognizing Patterns









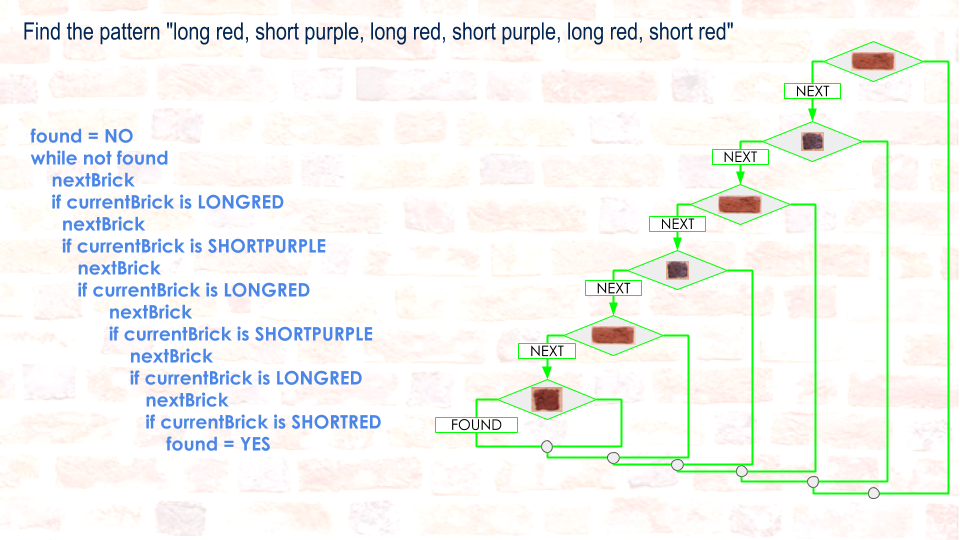

r R r R R R R R
R R p P p R p R p
R p r R r R p R p R
p p R p R p R p R p
R p R p R p R p R
R p R p R r R r R r
r R p R r R r R r R
R p R r R p R r R p
p R p R p R p R r R
R p R r R p R p R p
R r p R r R p R p
r p R p R r R p R
JavaScript Sidebar
JAVASCRIPT ASIDE: In JS an array such as ['r','R','P','p'} is treated the same as the string 'rRPp'. So, we can save some time and typing if we treat our pattern and our bricks as strings:
'rRrRRRRRRRpPpRpRpRprRrRpRpRppRpRpRpRpRpRpRpRpRRpRpRrRrRrrRpRrRrRrRRpRrRpRrRppRpRpRpRrRRpRrRpRpRpRrpRrRpRprpRpRrRpR'
'RpRpRr'
function search() {
var bricks = 'rRrRRRRRRRpPpRpRpRprRrRpRpRppRpRpRpRpRpRpRpRpRRp
RpRrRrRrrRpRrRrRrRRpRrRpRrRppRpRpRpRrRRpRrRpRpRp
RrpRrRpRprpRpRrRpR';
const pattern = 'RpRpRr';
var output = '';
//loop over places pattern could start
for (start=0; start<bricks.length-pattern.length; start++) {
// each scan begins with flag=false and current points at start
for (i=0; i<pattern.length; i++) {
//if current brick no match then start over
//if at end of pattern then we have a match
//otherwise, next brick
}
//if match, announce it
}
}
Repetition INF1339F21
By Dan Ryan
Repetition INF1339F21
- 368