Online Entity Resolution Using an Oracle
Donatella Firmani, Barna Saha, Divesh Srivastava
Outline
- Intro: ER with Oracle
- Motivation
- New metric for ER w/ Oracle
- Hybrid EM Strategy
- Experiments
- Conclusion
Intro: ER with Oracle
ER with Oracle
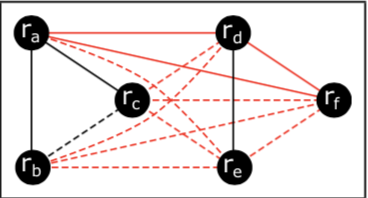
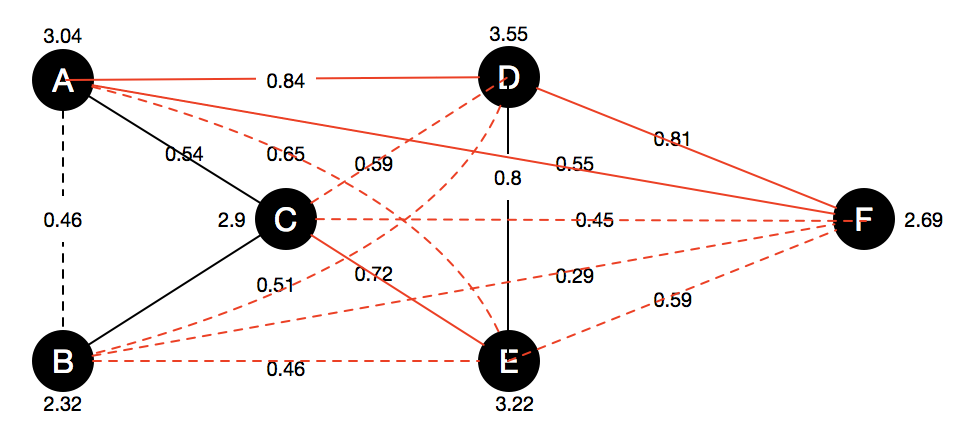
Entity resolution can be seen as connecting a graph in which vertices are records, black edges are matching relationship and red edges are non-matching.
How to solve it?
- What's the problem?
- What information do we have?
Problem setting
- Entities have transitivity.
- We already have probabilities.
- Crowd: using Oracle to abstract away crowd workers
- Objective (informally): Query as efficient as possible to Oracle, because of budget, time, manpower…
Problem
setting & characteristics
- Entities have transitivity: if \( a \) and \( c \) are the same things, \( a \) and \( d \) are not the same things, then \( a \) and \( c \) can not be the same things.
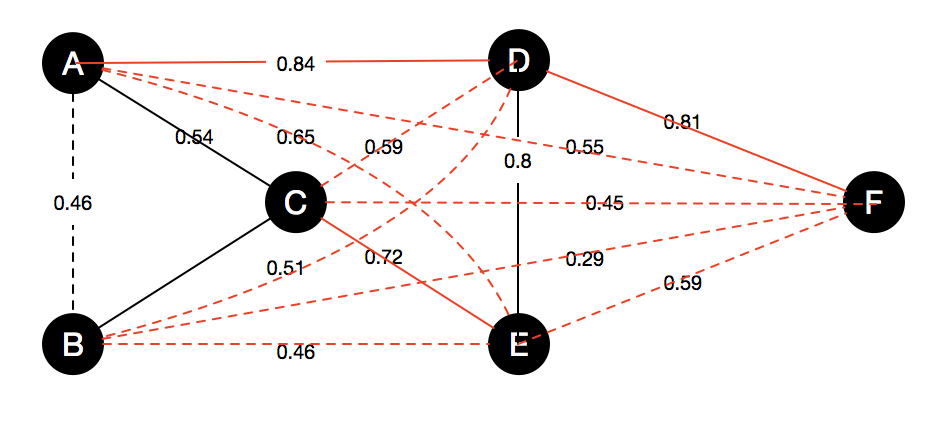
- We already have probabilities \( p \) for each pairs telling they are matching or not, e.g. \( p(r_a, r_b) = 0.46 \)
Problem setting & Oracle
Assuming oracle are 100% correct.
Motivation

* Black edges are matching relationship and red edges are non-matching.
* Solid edges are acquired from Oracle and dashed edges are inferred.
Only six pairs is needed for querying to Oracle:
\( (r_a, r_b) \), \( (r_a, r_c)\), \((r_d, r_e)\), \((r_a, r_d)\), \((r_a, r_f )\), \((r_d , r_f )\)
Order matters!
Previous:
\( (r_a,r_b) \), \( (r_a,r_c) \), \( (r_d,r_e)\), \((r_a,r_d)\), \((r_a,r_f)\), \((r_d,r_f)\).

Another ordering:
\( (r_a, r_d)\), \((r_a, r_f )\), \((r_d, r_f )\), \((r_d, r_e)\), \((r_a,r_b)\), \((r_a,r_c)\).
The recall would be 0 after labeling the first three record pairs, 0.25 after labeling the fourth record pair, 0.5 after labeling the fifth record pair, and 1.0 after labeling the sixth record pair.

Considering pairs with probabilities:
Matching:
\( p(r_d, r_e) = 0.80\), \(p(r_b, r_c) = 0.60\), \(p(r_a, r_c) = 0.54\), \( p(r_a, r_b) = 0.46\).
Non-matching: \(p(r_a, r_d) = 0.84\), \(p(r_d, r_f) = 0.81\), \(p(r_c, r_e) = 0.72\), \(p(r_a, r_e)=0.65\), \(p(r_c, r_d)=0.59\), \(p(r_e, r_f) = 0.59\), \(p(r_a, r_f)=0.55\), \(p(r_b, r_d) = 0.51\), \(p(r_b, r_e) = 0.46\), \(p(r_c, r_f) = 0.45\), \(p(r_b, r_f) = 0.29\)
A total of 7 pairs will be queried \((r_a,r_d)\), \((r_d,r_f)\), \((r_d,r_e)\), \((r_c,r_e)\), \((r_b,r_c)\), \((r_a,r_f)\), \((r_a,r_c)\), if using minimizing # queries strategy
Previous works:
The problem of previous works:
Higher probability node pairs may be non-matching.
New metric for ER w/ Oracle
Progressive recall
What is the progressive recall?
In an entity graph,
with \( E^+ \) as the ground truth of positive edges,
and \(E_T^+\) as the positive edges we can get with \( t = |T| \) queries and \(T\) is the set of the query.
Then the progressive recall will be defined as
\( precall(t) =\sum_{t'=1}^t recall(t') \), and \(precall^+(t)=\sum_{t'=1}^t recall^+(t')\).
A \(recall\) of \(T\) can be defined as \( recall(t) = \frac{|E^+_T|}{|E^+|} \), and \( recall^+(t) = \frac{|E^+_{T^+}|}{|E^+|} \)
Intuitively, progressive recall is the area under the recall curve
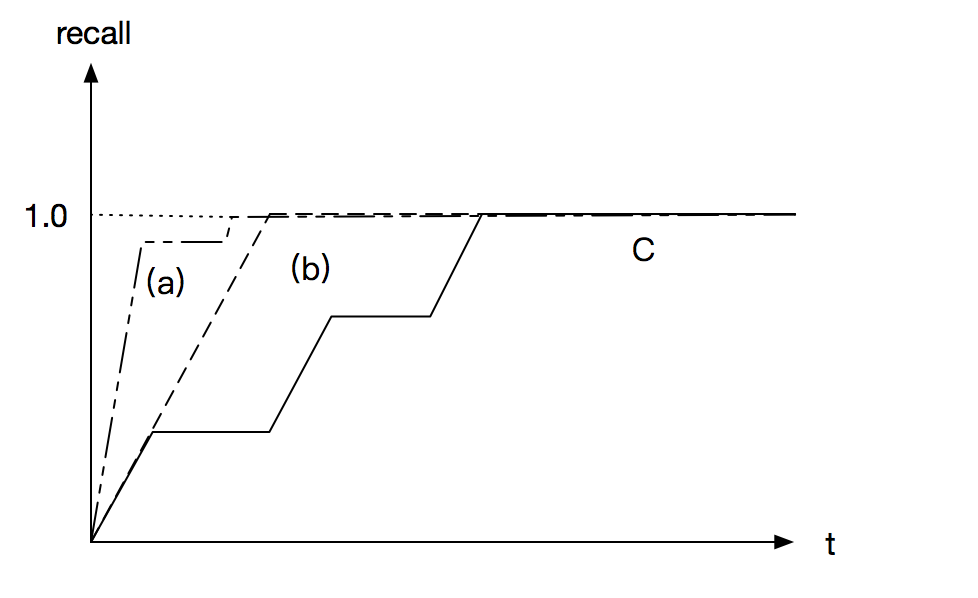
Intuitively, progressive recall is the area under the recall curve

Although all of (a), (b) and (c) can achieve recall 1 eventually, (a) is better than (b) and (c)

The best strategy is asking all positive questions first then negative questions (comparing (b) and (c)). And ask most efficient questions first (comparing (a) and (b)
Intuitively, progressive recall is the area under the recall curve
Although all of (a), (b) and (c) can achieve recall 1 eventually, (a) is better than (b) and (c)
Hybrid EM
Edge noise model
For matching edges, with probability \((1- \frac{\alpha}{n} )\), \( \alpha \gt 0 \) the score is above 0.7, and the remaining probability mass is distributed uniformly in \([0, 0.7)\).
For non-matching edges, with probability \( (1-\frac{\beta}{n}) \) , \( \beta \gt 0 \), the score is below 0.1 and the remaining n probability mass is distributed uniformly in \( (0.1,1] \).
Prior strategies
Wang et al.
\( O(log^2n)-approximation\) under edge noise model
\( \Omega(n)-approximation\) under progressive recall

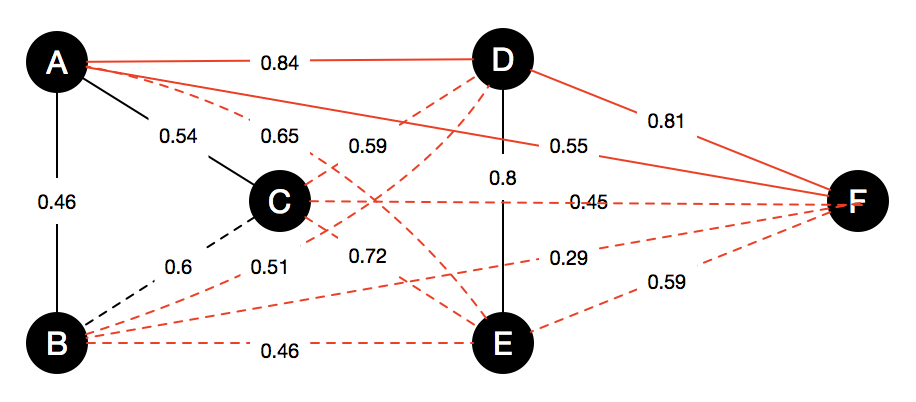
Strategy: High probability pair first.
A total of 7 pairs will be queried \((r_a,r_d)\), \((r_d,r_f)\), \((r_d,r_e)\), \((r_c,r_e)\), \((r_b,r_c)\), \((r_a,r_f)\), \((r_a,r_c)\).
Vesdapunt et al.
\( O(log^2n)-approximation\) under edge noise model
\( \Sigma(\sqrt n) \) under progressive recall

Strategy: High probability node first.
A total of 7 pairs will be queried \((r_e,r_d)\), \((r_a,r_d)\), \((r_c, r_e)\), \((r_c, r_a)\), \((r_f, r_d)\). \((r_f, r_a)\), \((r_b, r_c)\).
The objective of these 2 algorithms upon is minimizing the total number of questions to the oracle, not progressive recall.
Strategy maximizing PRecall
A maximized PRecall strategy \(S^*\) is:
- Presume we already know the ground truth
- For each cluster \(C_k\) in the graph (which is a same real-world entity), we ask \(|C_k|\) questions to the Oracle.
- Questions are asked in the sequence of \( C_1, C_2, ..., C_k \), where \( |C_k| \) has a decreasing order.
- Finally asking \( \binom k2 \) non-matching questions.
- Ideally, \(s^*\) will ask \(n - k + \binom k2 \) questions
Benefits
In order to ask questions along with the increasing direction of recall, we use benefit to measure it.
\( b_e \) is the benefit of a edge between \(u\) and \(v\), calculated as \( |c_T(u) | * | c_T(v) |* p(u,v) \)
\(b_v\) is the benefit of a node when adding this node to the \(P\) set.
\(b_{vc}(v,c) = p_v(v,c) * |c|\)
\(b_v(v,P) = \max b_{vc}(v,c)\)
A greedy algorithm is obtained if every question asked maximizes the benefit.
Algo 3
Optimum progressive recall

Strategy: choosing edge which has maximum benefit to ask
A total of 6 pairs will be queried \((r_a,r_d)\), \((r_d,r_f)\), \((r_d,r_e)\), \((r_c,r_e)\), \((r_b,r_c)\), \((r_a,r_c)\).

Algo 3
Optimum progressive recall

Strategy: choosing edge which has maximum benefit to ask
A total of 6 pairs will be queried \((r_a,r_d)\), \((r_d,r_f)\), \((r_d,r_e)\), \((r_c,r_e)\), \((r_b,r_c)\), \((r_a,r_c)\).

Why?
Algo 3
Optimum progressive recall

Strategy: choosing edge which has maximum benefit to ask
\(b_e(r_a,r_c)\) = 2 * 1 * 0.54 = 1.08
\(b_e(r_a, r_c)\) = 1 * 1 * 0.55 = 0.55

Algo 4

Optimum progressive recall
Strategy: First choosing max benefit node then choosing maximum benefit edge to ask.
if \(w = 1\):
if \( \tau = n\) and \(\theta = 0\) then \(s_{hybrid} = s_{vesd} \)
if \(\tau = 0\) or \(\theta = n\), then \(s_{hybrid} = s_{wang} \)
Experiments
Datasets
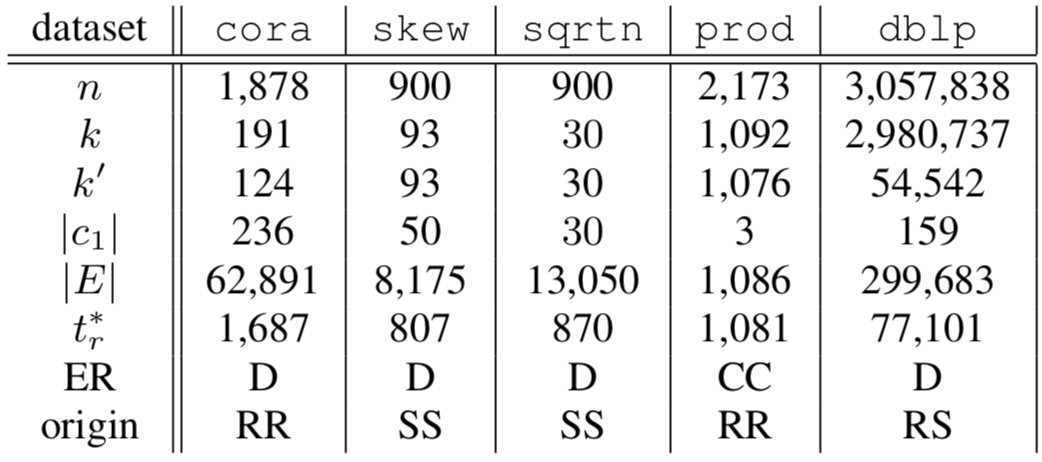
n: num of records
k: num of entities (clusters)
k': num of non-singleton entities (clusters)
\(|c_1|\): largest clusters
\(t^*_r\): size of the spanning forest
ER: dirty or clean-clean
origin: real or synthetic of data
Datasets

R: # record pairs
\( n' \): \( \binom n2 = \lfloor R \rfloor \)
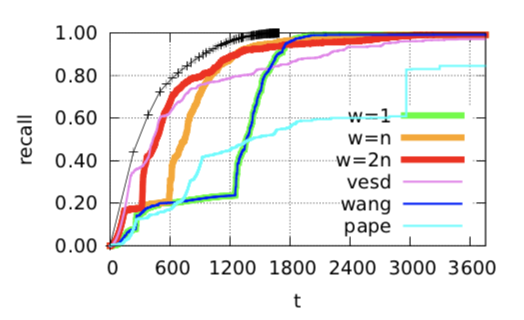
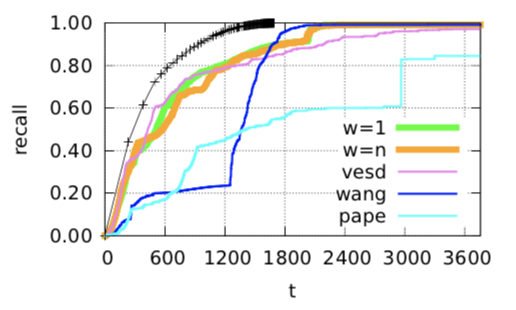
\(s_{edge}\)
\(s_{hybrid}\)
\(s_{hybrid} \) is better than \(s_{edge}\) with same parameter, but...
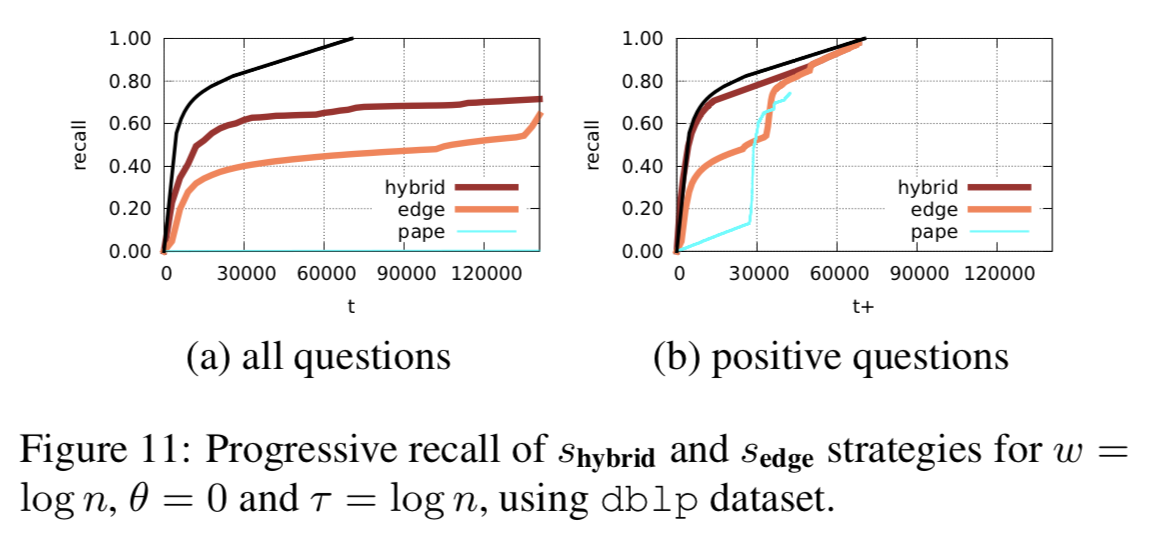
Hybrid has the best performance
In large dataset

A visualization of each algorithm
Conclusion
- Optimizing toward progressive recall is a more general form of 2 previous work.
- Algorithm towards maximizing progressive recall performs better than previous work
Opinions?
- Strong assumption for noise model
- Progressive recall may not overwhelm in all circumstance comparing to # of queries.
- Experiment on synthesized data?
Opinions?
Online Entity Resolution Using an Oracle
By Weiyüen Wu
Online Entity Resolution Using an Oracle
- 845



