A quick tour of Neural Networks for Time Series
Follow slides live at: slides.com/eiffl/nn-ts/live
Francois Lanusse @EiffL
What are we trying to do?
Credit: PLAsTiCC team
- The data structure we are considering is time series:
- Can be irregularly sampled
- Can have large gaps
- Can come from several modalities (e.g. different bands at different times)
- From given time series, typicaly you would perform classification or regression
- We want to use a Neural Network for that
A generic problem
What we will cover today:
-
Recurrent Neural Networks:
- LSTM
- GRU
-
Convolutional Neural Networks:
- 1D CNN
- TCN
Recurrent Neural Network Approach
Illustrations from this excellent blog: https://colah.github.io/posts/2015-08-Understanding-LSTMs/
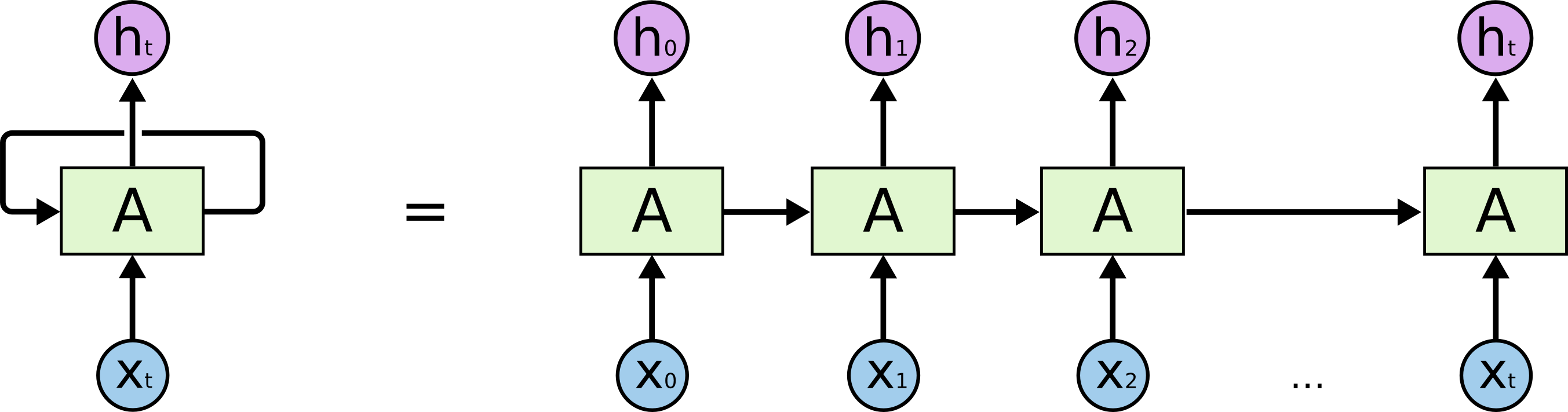
What does an RNN look like?
\left(
\begin{matrix}
h_t\\
c_t
\end{matrix}\right) = f_\theta \left( \begin{matrix}
x_t\\
c_{t-1}
\end{matrix} \right)
c_0
c_{t-1}
c_1
- is the RNN cell
- is the input at step t
- is the output at step t
- is the cell state at step t
\mathbf{A}
x_t
h_t
c_t
The problem of long-term dependencies
h_t = f_\theta( f_\theta( f_\theta(...., x_{t-3} ), x_{t-2}), x_{t-1})
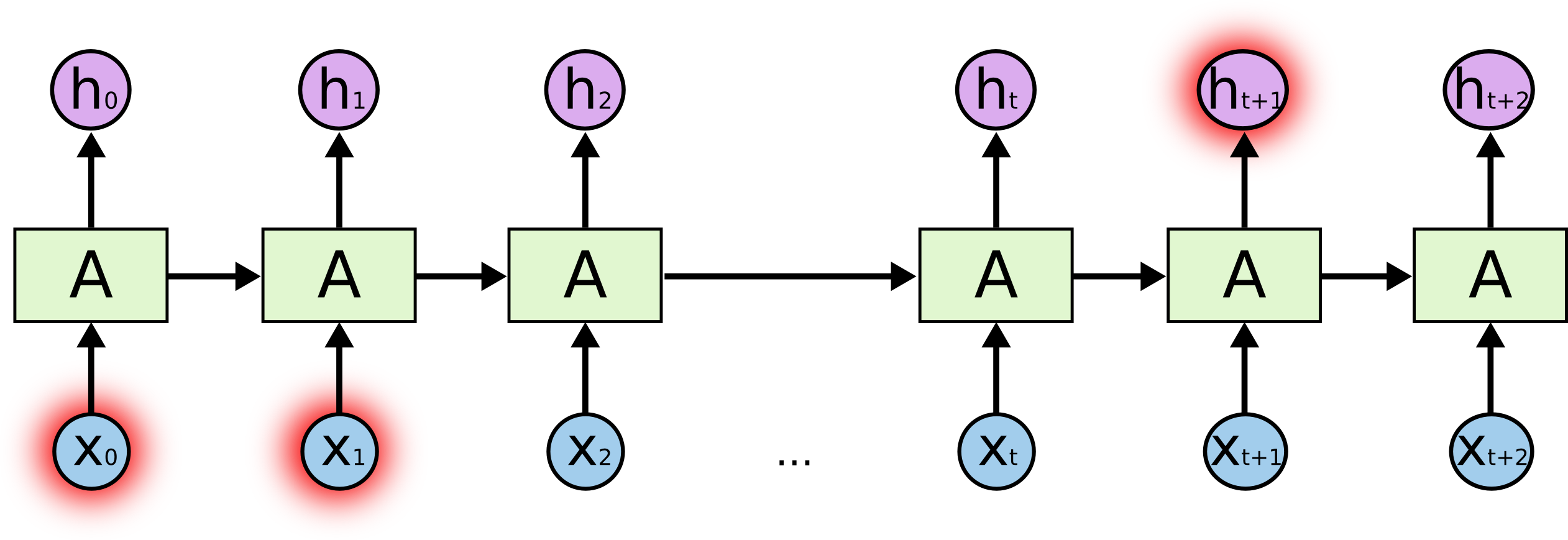
- Information has to survive through many compositions of the same function
- Typical problems of vanishing gradients, and decaying/exploding modes
- Practical RNNs need a mechanism to preserve long term memory
The Long Short Term Memory RNN
(Hochreiter & Schmidhuber, 1997)
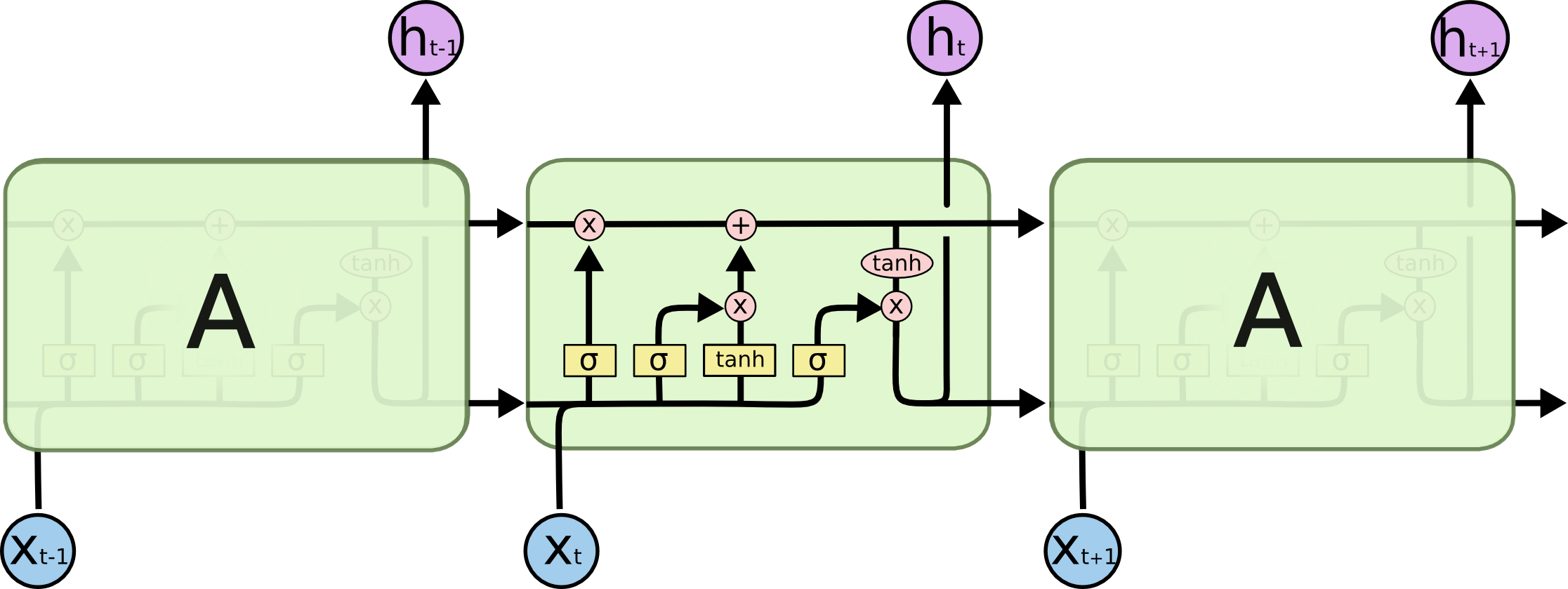
The main idea: Preserve the information by default, update if necessary
1) Control of the state
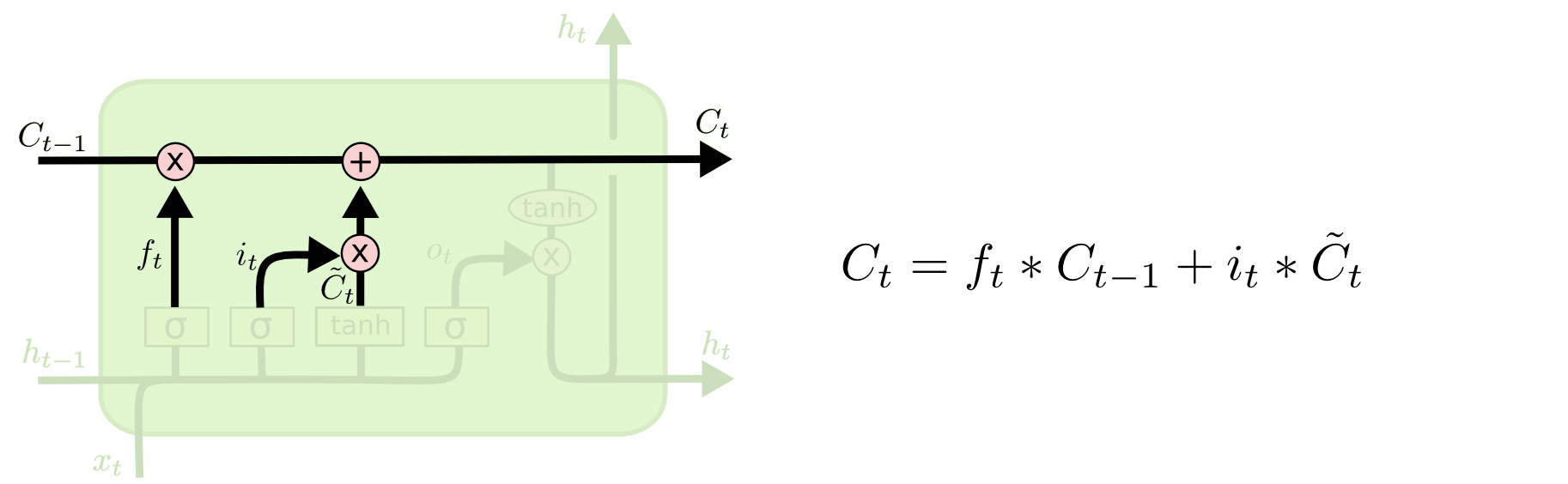
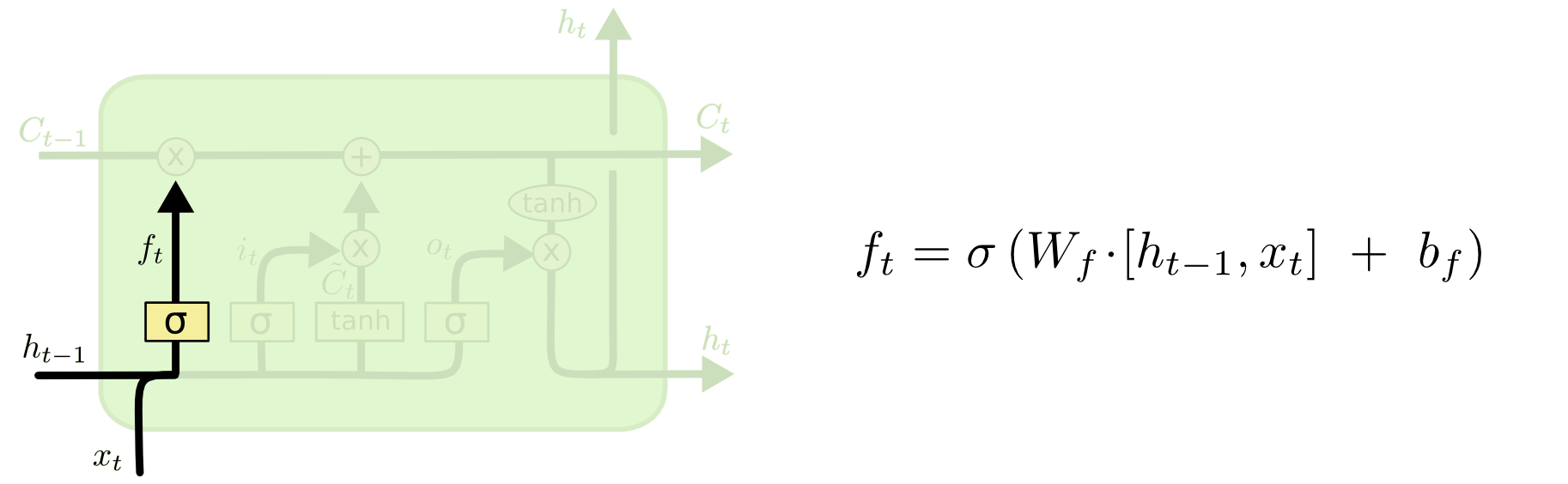
- The state of the cell can be set to 0 by the forget gate , while the input gate allows new information to be added to the state.
- The forget gate is controlled by the previous output and new input
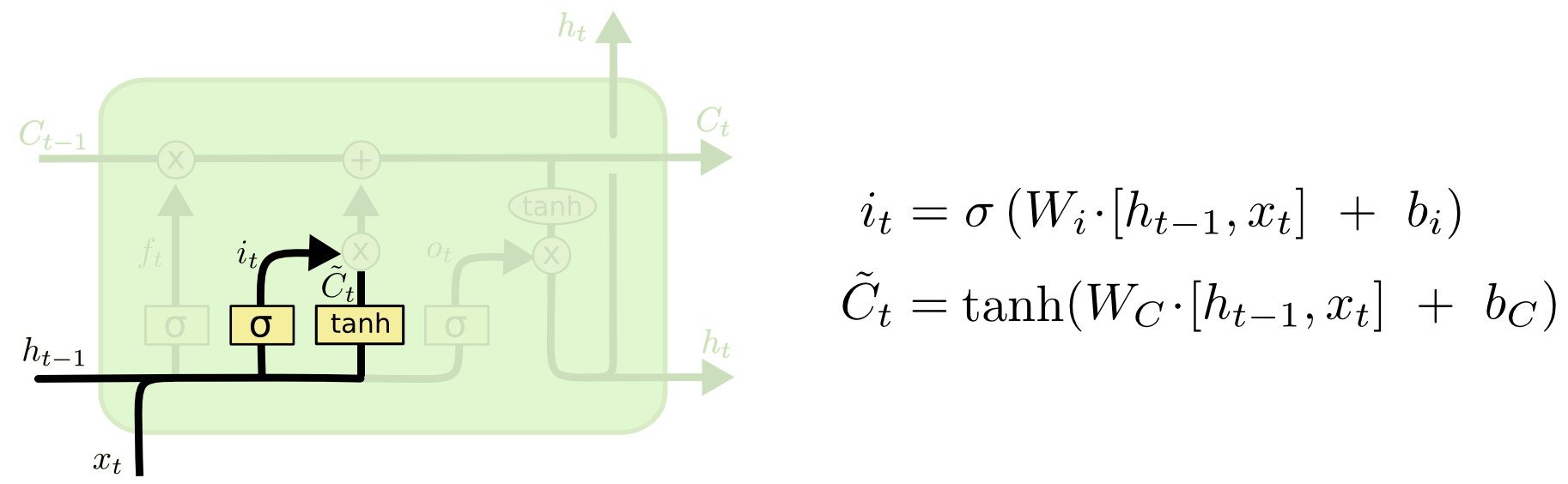
- The input gate is controlled the same way
The cell state update is also the result of previous output and new input
f_t
i_t
2) Cell Output
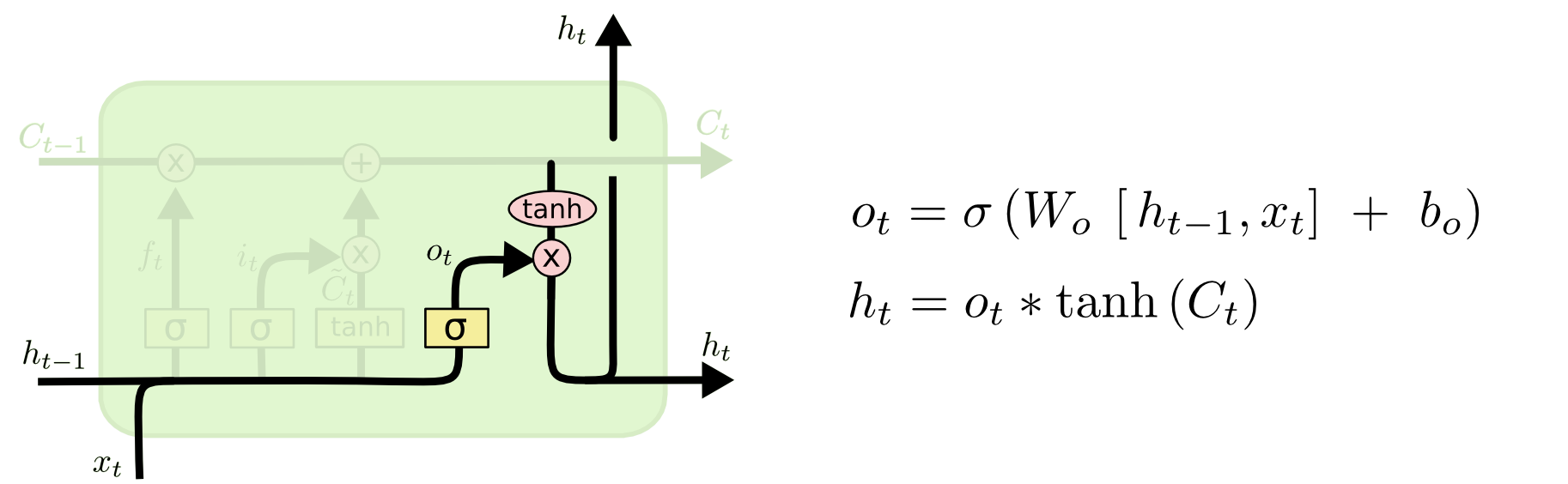
- The output uses previous output, new input, and is gated by cell state
The Gated Recurrent Unit RNN,
(Cho et al. 2014)
Compared to the LSTM:
- Merges cell state with hidden/output state
- Merges forget and input gates into a single update gate
LSTM
Let's build an RNN-based model
RNN
x_0
c_0
h_0
RNN
x_1
c_1
h_1
RNN
x_2
c_2
h_2
RNN
x_3
c_3
h_3
Dense
\hat{y}
\mathcal{L} = \parallel y - \hat{y} \parallel_2^2
The simplest RNN regression model
import tensorflow as tf
# Create model instance
model = tf.keras.Sequential()
# Add layers to your model
model.add(layers.LSTM(128, input_shape=(10,)))
model.add(layers.Dense(32))
# Compile the model with specific optimizer and loss function
model.compile(optimizer='rmsprop', loss='mse')
RNN
x_0
RNN
x_1
RNN
x_2
RNN
x_3
Dense
\hat{y}
\mathcal{L} = \parallel y - \hat{y} \parallel_2^2
Let's go deeper! Stacked RNNs
RNN
RNN
RNN
RNN
RNN
h_0
RNN
h_1
RNN
h_2
RNN
h_3
RNN
x_0
RNN
x_1
RNN
x_2
RNN
x_3
Dense
\hat{y}
\mathcal{L} = \parallel y - \hat{y} \parallel_2^2
Causality is overrated! Bi-directional RNNs
RNN
RNN
RNN
RNN
Pooling
-
Deep Recurrent Neural Networks for Supernovae Classification,
Charnock & Moss, 2017
Some examples of RNNs in the (astro) wild
-
SuperNNova: an open-source framework for Bayesian,
Neural Network based supernova classification,
Moller & de Boissiere, 2019
Main takeaways for RNNs
- Naturally adapted to sequences, they do not require regularly sampled data.
- Despite many improvements and practical architectures, training a recurrent neural network remains an inherently challenging task.
- RNNs do not benefit from the same inductive biases as CNNs for time series
- No built-in notion of time-scales!
- You need to manually encode time one way or another
Convolutional Neural Networks approach
Credit: https://arxiv.org/abs/1809.04356
Convolutional Neural Network for 1D data
Several problems of this approach:
- For sequence modeling, causality (i.e. auto-regressiveness ) of the model is important
- Limited receptive field, i.e. scales accessible to the neural network
WaveNet: Temporal (i.e. Causal) Dilated Convolutions
(van den Oord, et al. 2016)
y = f( (W \ast x)_{\downarrow 2} + b)
For a temporal convolution W is a causal filter
Examples of 1D CNNs in the (astro) wild
- PELICAN: deeP architecturE for the LIght Curve ANalysis, (Pasquet et al. 2019)
Main takeaways for CNNs
-
CNNs do not have the issue of long term memory
retention
- CNNs require a constant data rate,
how do you handle irregular samples?- Typically, you pad with zeros and hope
for the best :-)
- Typically, you pad with zeros and hope
- Convolutions are appropriate operations for 1D data
- This inductive bias means you achieve high quality results with relatively low number of parameters.
Conclusion
- RNNs and CNNs have both been used to analyse time series in astrophysics.
- They can be used in many different ways with varying results depending on the application.
- They can be used in many different ways with varying results depending on the application.
- Properly handling time-dependency is in both cases an important factor
- RNNs are so 2016... Attention is all you need
Thank you!
Bonus: Check out a complete example of star/quasar classification by LSTM here
A quick tour of Neural Networks for Time Series
By eiffl
