Basisconcepten

$|A| = |B|$

Verzameling $A$ en $B$ hebben evenveel elementen.
$ \Leftrightarrow $ er bestaat een bijectie tussen $A$ en $B$

Kardinaliteit $|S|$
Het aantal elementen in een verzameling $S$

We zijn geïnteresseerd in de kardinaliteit van eindige én oneindige verzamelingen.

Bij een eindige verzameling is "de kardinaliteit bepalen" hetzelfde als "het aantal elementen tellen".
De "bijectie-definitie" zorgt dat we ook betekenisvolle uitspraken kunnen doen over "het aantal" elementen in een oneindige verzameling.

N.b. Als je het aantal elementen telt van verzameling $V=\{A,B,C\}$, dan maak je (impliciet) een bijectie tussen $V$ en de verzameling $T=\{1,2,3\}$.
Je "bewijst" de gelijke kardinaliteit door een concreet voorbeeld te geven van een bijectie
$T \rightarrow V$, vertrekkende van een verzameling $T$ met gekende kardinaliteit, $|T|=3$.

Basisconcepten

Kardinaliteit van meerdere verzamelingen:
- Tel de doorsnede niet dubbel,
  $|A \cup B| = |A| + | B| - |A \cap B|$
- in het algemeen: inclusie-exclusie-principe,
  $$|\bigcup_{i=1}^{n} V_i| = \sum_{I \subseteq \{1, 2, \ldots n\}, |I|\,oneven} | \bigcap_{i \in I}V_i| - \sum_{I \subseteq \{1, 2, \ldots n\}, |I|\, even} | \bigcap_{i \in I}V_i|$$
Kardinaliteit cartesisch product,
$|W \times F| = |W| \cdot |F|$
Kardinaliteit machtsverzameling,
$|\mathcal{P}(A)| = 2^{|A|}$

Bij het maken van een willekeurige deelverzameling $R \subseteq A$, maak de keuze $\forall x \in A$ of $x \in R $.

Dat geeft $|A|$ binaire keuzes.

Basisconcepten

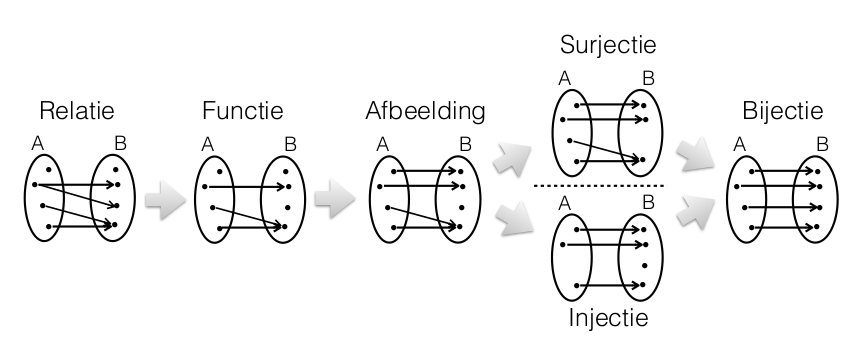
Aantal afbeeldingen van $A$ naar $B$
- $|B^A| = |B|^{|A|}$
- Een groep studenten $S$ bestelt een rondje (1 consumptie pp.)
  op café met menu $M$. Aantal mogelijke bestellingen $=|M|^{|S|}$
Aantal injecties van $A$ naar $B$
- faculteit $n! = n \cdot (n-1) \cdot (n-2) \cdots 2 \cdot 1$
- $\frac{n!}{(n-m)!}$
- Aantal manieren om $m$ kindjes in
  $n$ botsauto's te krijgen
Aantal bijecties van $A$ naar $B$, $|A| = |B| = n$
- $n!$
- Aantal permutaties van $A$
Aantal deelverzamelingen van $A$ met grootte $m$, als voor $A$ zelf geldt $|A|=n$.
- $\frac{n!}{m!(n-m)!}$
- Binomiaalcoëfficient: $C^m_n = {{n}\choose{m}} = \frac{n!}{m!(n-m)!}$
- Aantal mogelijke manieren om een lottoformulier in te vullen.

Basisconcepten

Voor oneindige verzamelingen: lees het Hilbert-hotel (zie cursus)
Kardinaliteit van natuurlijke getallen $\mathbb{N}$
- $|\mathbb{N}| = \aleph_0$
- $\aleph_0$ is geen natuurlijk getal
- $|\mathbb{N}| = |\mathbb{Z}| = |\mathbb{Q}| $
  want er bestaan bijecties.
- Deze verzamelingen zijn aftelbaar oneindig
Kardinaliteit reële getallen $\mathbb{R}$
- $|\mathbb{N}| < |\mathbb{R}| $
- Het diagonalisatiebewijs van Cantor toont aan dat men de elementen van $\mathbb{R}$ niet kan oplijsten, dus is een bijectie met $\mathbb{N}$ onmogelijk.
- Zo'n verzameling is onaftelbaar oneindig