A few things quantum
01: Spin
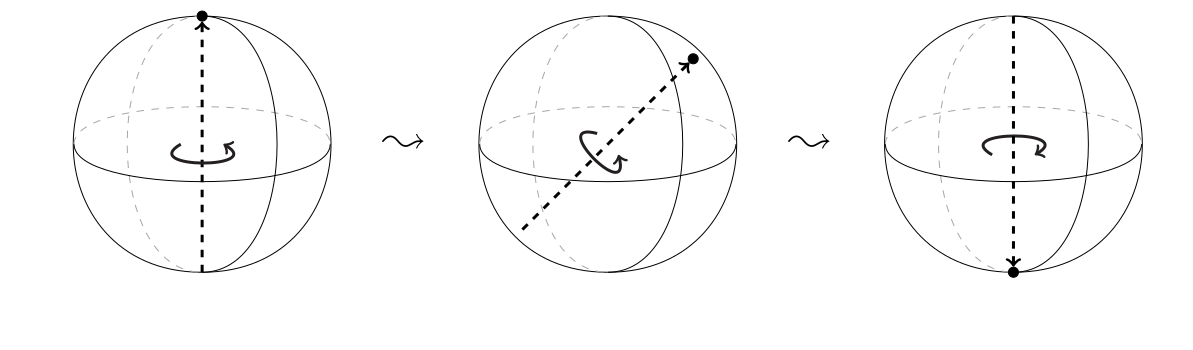
- Magnet spinning around an axis
- Rotation of the entire system:
Clockwise to counter-clockwise
01: Spin
01: Spin
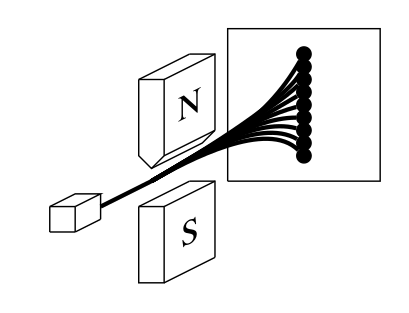
Electromagnetism: spinning magnets in an inhomogeneous magnetic field deflect,
depending on (counter)clockwise rotation
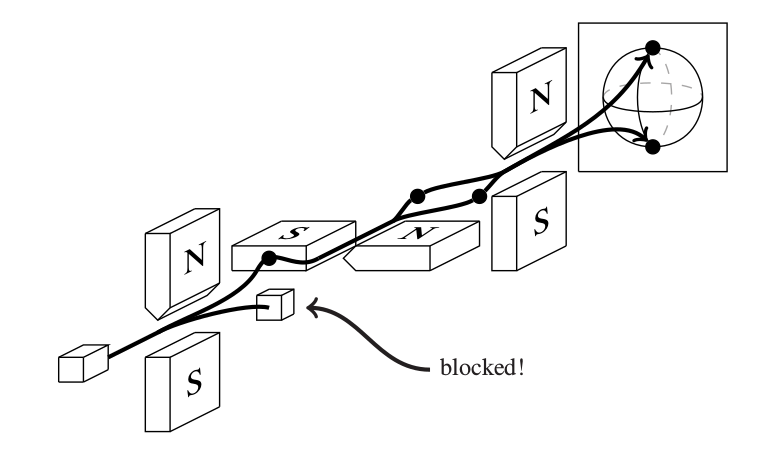
Stern-Gerlach apparatus
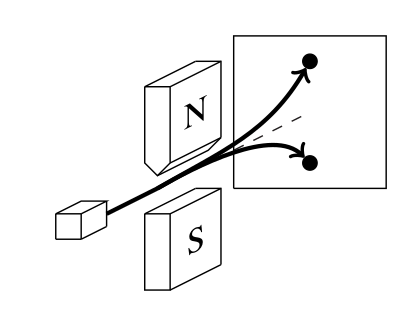
Quantum case:
No spectrum anymore! Either you are spin up or spin down, but nothing in between.
01: Spin
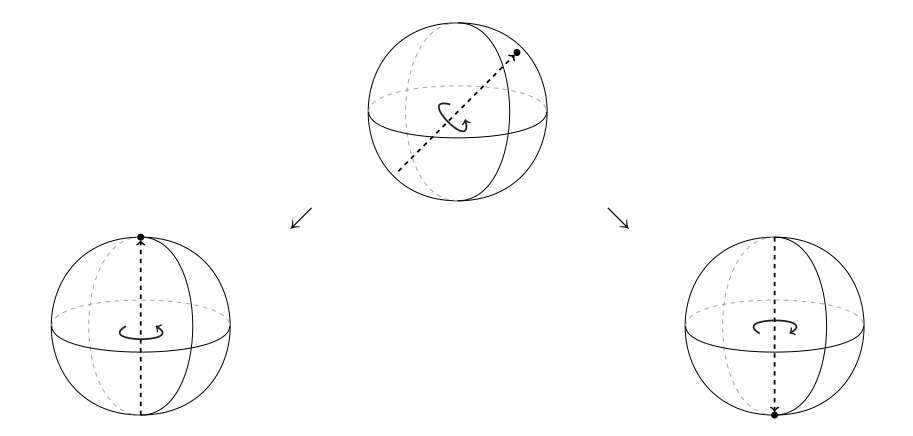
I'm cutting some corners here, but this is our first meeting with a unique quantum phenomenon called collapse
01: Spin
M
M
01: Spin
02: Cbits and Qbits
02: Cbits and Qbits
Now, we need to focus and distinguish 3 things:
1. Bits
2. Cbits
3. Qbits
1. Bits
2. Cbits
3. Qbits
Information
Logic
Mathematics
Encoding a message
Shannon
02: Cbits and Qbits
1. Bits
2. Cbits
3. Qbits
02: Cbits and Qbits
1
0
1. Bits
2. Cbits
3. Qbits
Light on/off
Transistor
Electronics
Physical System
Turing
02: Cbits and Qbits
1. Bits
2. Cbits
3. Qbits
02: Cbits and Qbits
1. Bits
2. Cbits
3. Qbits
Spin up/down
Quantum-physical System
Feynmann/Deutsch/Schor
02: Cbits and Qbits
1. Bits
2. Cbits
3. Qbits
02: Cbits and Qbits
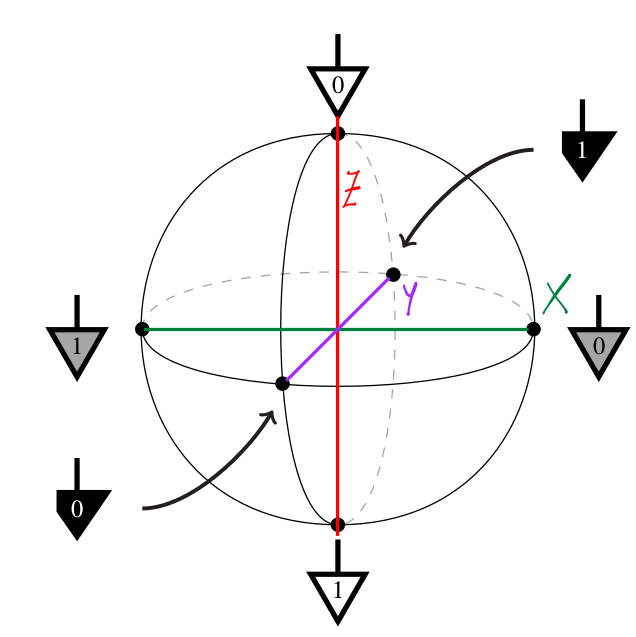
02: Cbits and Qbits
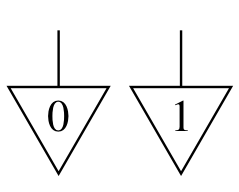
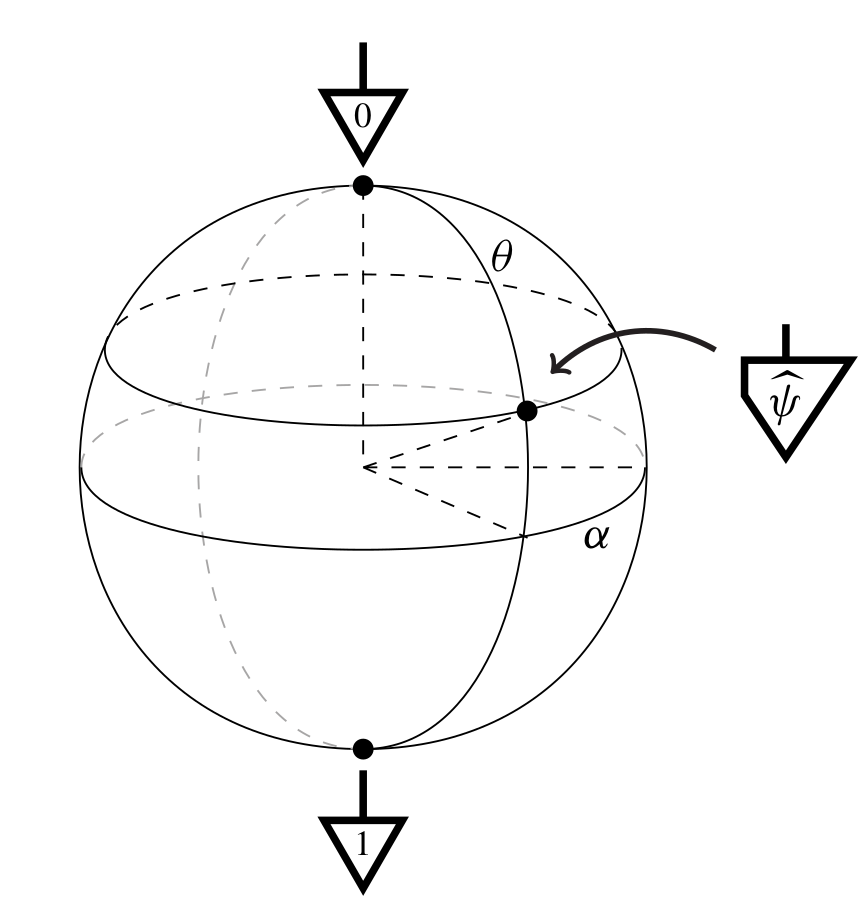
Cbit
Qbit
| 0 \rangle =
\begin{pmatrix}
1 \\
0
\end{pmatrix}
| 1 \rangle =
\begin{pmatrix}
0 \\
1
\end{pmatrix}
| \hat{\psi} \rangle =
\begin{pmatrix}
\psi_0 \\
\psi_1
\end{pmatrix}
\psi_0, \psi_1 \in \mathbb{C}, |\psi_0|^2 + |\psi_1|^2 = 1
| \kappa \rangle =
\begin{pmatrix}
\kappa_0 \\
\kappa_1
\end{pmatrix}
\kappa_0, \kappa_1 \in \{0,1\}
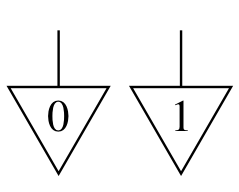
02: Cbits and Qbits
Qbit
| \hat{\psi} \rangle =
\begin{pmatrix}
\psi_0 \\
\psi_1
\end{pmatrix}
\psi_0, \psi_1 \in \mathbb{C}, |\psi_0|^2 + |\psi_1|^2 = 1
Again cutting some corners, but this is what people call superposition.
03: Quantum entanglement
03: Quantum entanglement
``God does not play dice''
- Albert E.
``A moving clock is slower'' (SR)
- Albert E.
``oh also, spacetime is a 4D manifold'' (GR)
- Albert E.
03: Quantum entanglement
``God does not play dice''
- Albert E.
Things, are real
Things are, in spacetime
Realism
Localism
03: Quantum entanglement
``God does not play dice''
- Albert E.
Realism
Localism
Turns out in QM you have to give up one!
(More than dice throwing, this was Einstein's actual problem with QM)
03: Quantum entanglement
| \hat{\psi_1} \rangle = \alpha |0 \rangle + \beta |1 \rangle
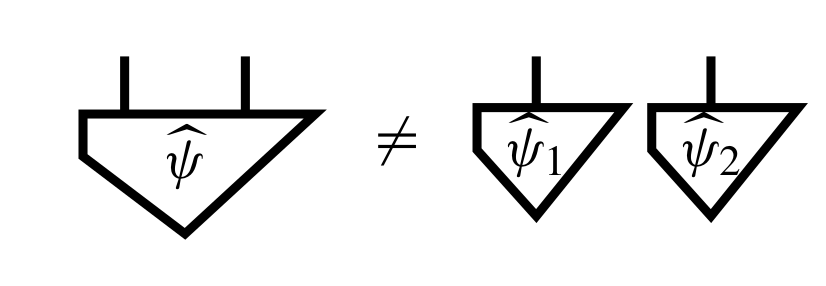
Remember, a single qubit looks like:
= \begin{pmatrix}
\alpha \\
\beta
\end{pmatrix}
03: Quantum entanglement
| \hat{\psi_1} \rangle = \alpha |0 \rangle + \beta |1 \rangle \\
= \begin{pmatrix}
\alpha \\
\beta
\end{pmatrix}
| \hat{\psi_2} \rangle = \gamma |0 \rangle + \delta |1 \rangle \\
= \begin{pmatrix}
\gamma \\
\delta
\end{pmatrix}
03: Quantum entanglement
=
= \alpha \gamma | 00 \rangle + \alpha \delta | 01 \rangle + \beta \gamma | 10 \rangle + \beta \delta | 11 \rangle
(\alpha |0\rangle + \beta | 1 \rangle)
| \hat{\psi} \rangle =
(\gamma |0\rangle + \delta | 1 \rangle)
\otimes
= \begin{pmatrix}
\alpha \gamma \\
\alpha \delta \\
\beta \gamma \\
\beta \delta\\
\end{pmatrix}
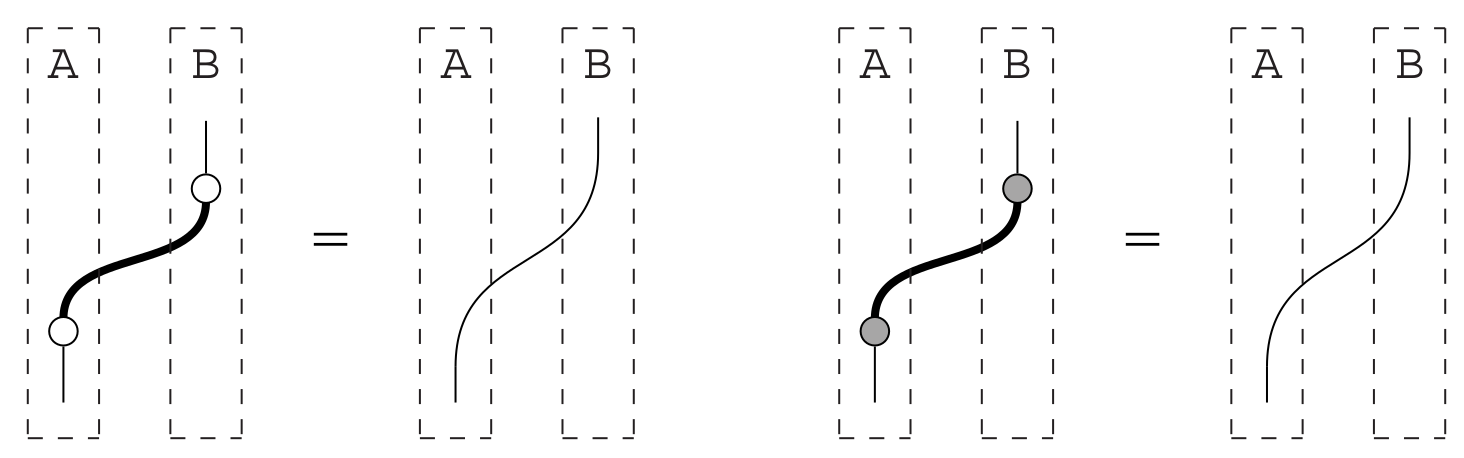
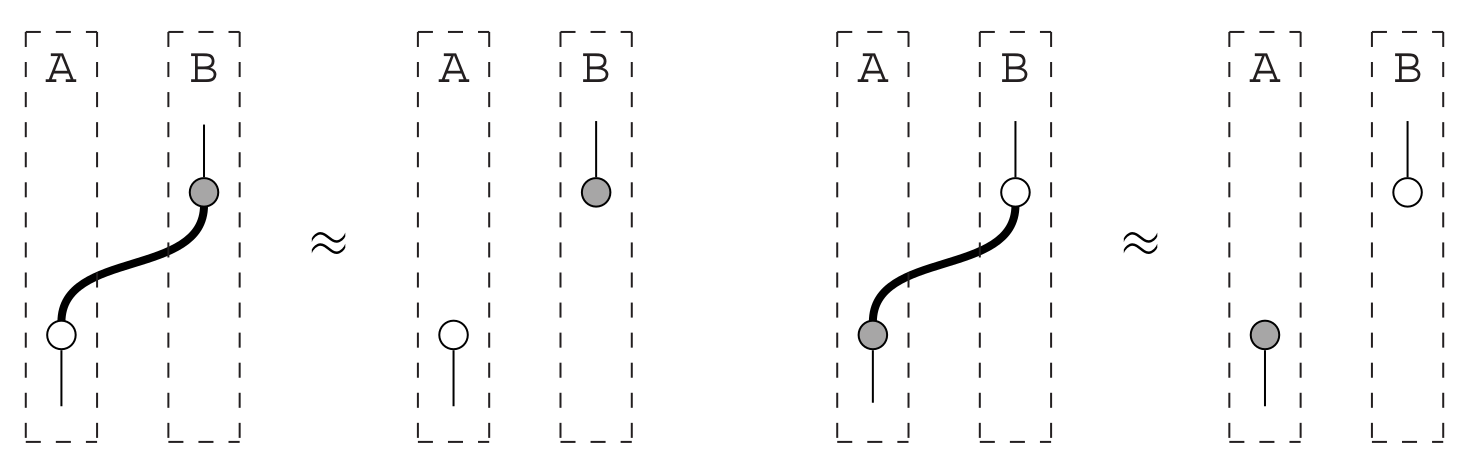
Composing systems goes via the tensor product
03: Quantum entanglement
\neq
| \hat{\psi} \rangle =
\begin{pmatrix}
\psi_{00} \\
0 \\
0 \\
\psi_{11} \\
\end{pmatrix}
= \begin{pmatrix}
\alpha \gamma \\
\alpha \delta \\
\beta \gamma \\
\beta \delta\\
\end{pmatrix}
\Rightarrow
Composing systems goes via the tensor product
?
\alpha \delta \beta \gamma = 0
\alpha \gamma \beta \delta = 0
03: Quantum entanglement
=
\begin{pmatrix}
\psi_{00} \\
0 \\
0\\
\psi_{11} \\
\end{pmatrix}
\neq
=
``Bell State''
= \psi_{00} | 00 \rangle + \psi_{11} | 11 \rangle
entanglement
03: Quantum entanglement
| \hat{\psi} \rangle =
\begin{pmatrix}
\psi_{00} \\
\psi_{01} \\
\psi_{10} \\
\psi_{11} \\
\end{pmatrix} =
\begin{pmatrix}
\psi_{00} \\
0 \\
0\\
\psi_{11} \\
\end{pmatrix}
04: Quantum communication
04: Quantum communication
Now, we're experts in superposition, collapse and entanglement
...but so what?
04: Quantum communication
\psi
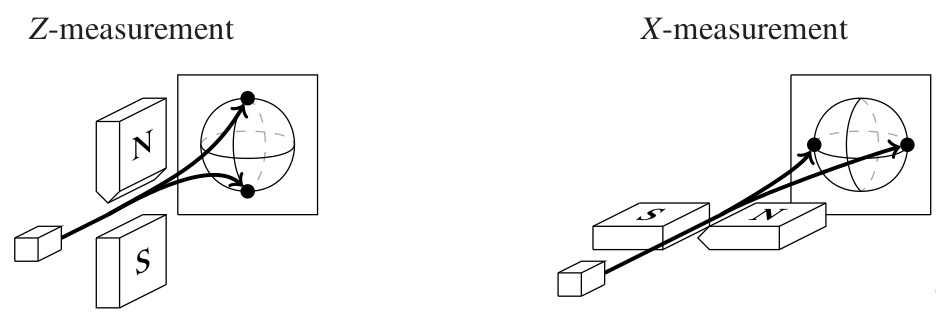
Z-measurement
Q-channel
Q-state
C-channel
04: Quantum communication
\psi
collapse
superposition
04: Quantum communication
\psi
\psi
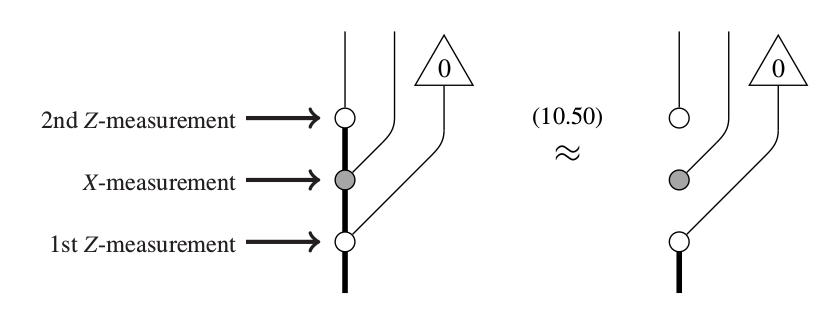
Z-measurement
X-measurement
04: Quantum communication
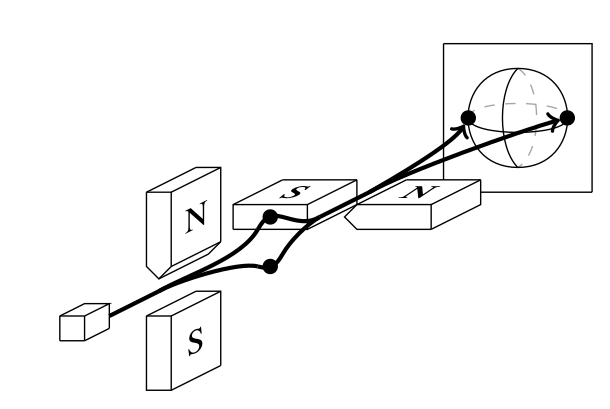
04: Quantum communication
=
Since you collapse on Z,
your state loses ALL information regarding X.
This is an example of complementarity
04: Quantum communication
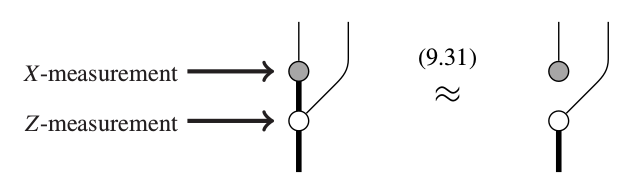
04: Quantum communication
04: Quantum communication
BB84
Alice wants to send random bits to Bob,
over a Q-channel.
04: Quantum communication
BB84
Alice wants to send random bits to Bob,
over a Q-channel.
04: Quantum communication
BB84
Alice wants to send random bits to Bob,
over a Q-channel.
Evil Donald wants to eavesdrop!
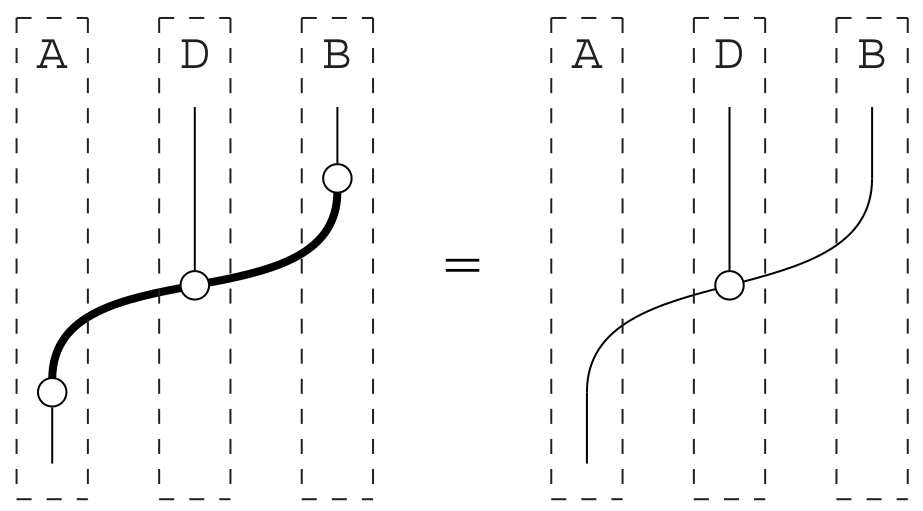
04: Quantum communication
BB84
Alice wants to send random bits to Bob,
over a Q-channel.
Evil Donald wants to eavesdrop!
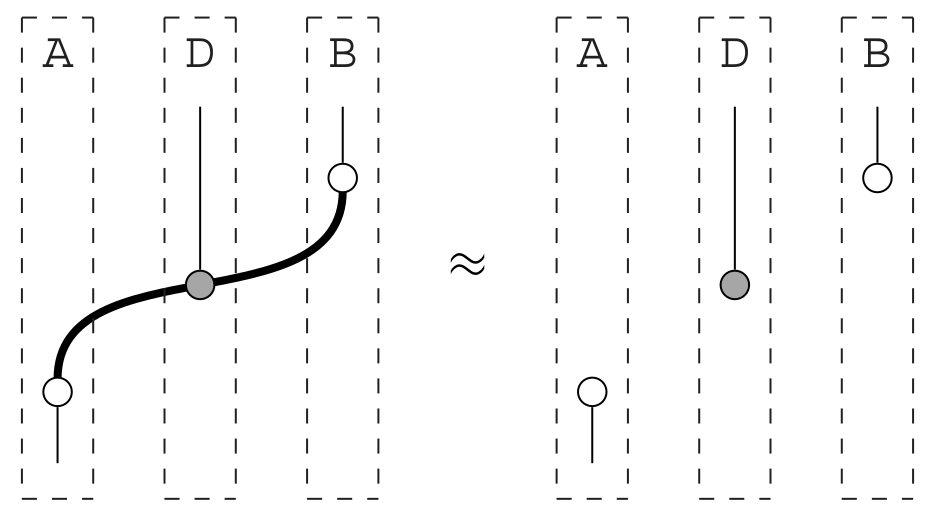
05: Quantum computation
05: Quantum Computation
Can all this quantum magic give us computing magic?
Yes! Do 2 things:
1. Exploit superposition
2. Fight collapse
05: Quantum Computation
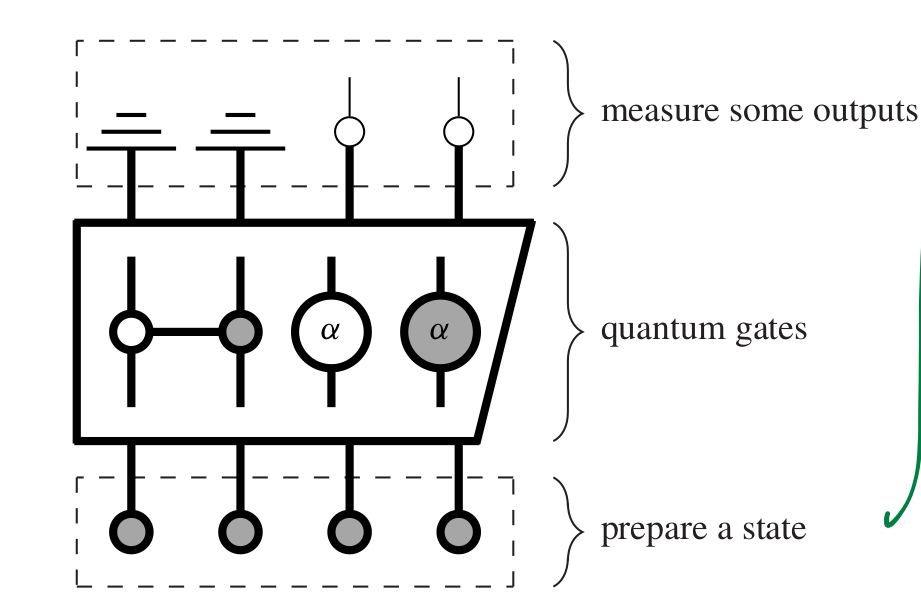
05: Quantum Computation
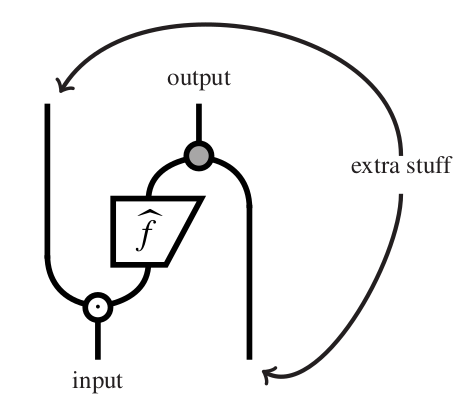
05: Quantum Computation
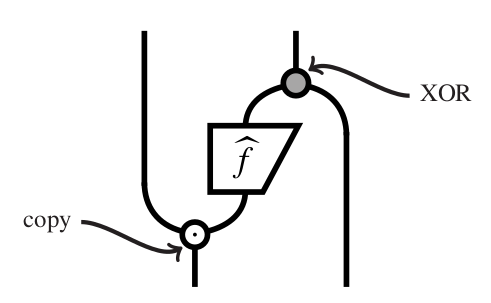
05: Quantum Computation
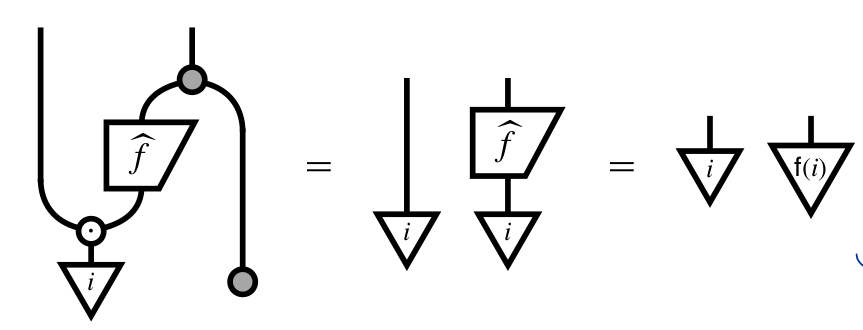
05: Quantum Computation
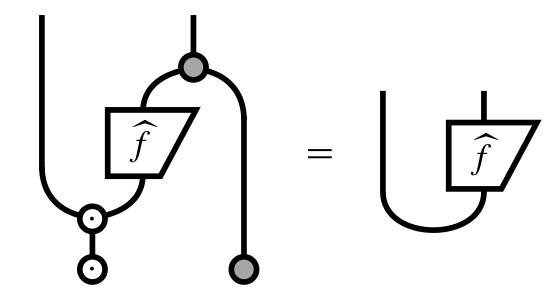
Uniform superposition
05: Quantum Computation
intro-quantum
By eliavw
intro-quantum
smilee presentation
