https://github.com/eli-jordan/fp-principles

Clone the above repo and import into your favorite editor.

Why FP Matters

Eli Jordan

Game Plan

  • What is functional programming
     
  • Human problem solving
     
  • Compositionality
     
  • Modularity / Maintainability / Testability

What Is Functional Programming?

  • Programming with pure functions

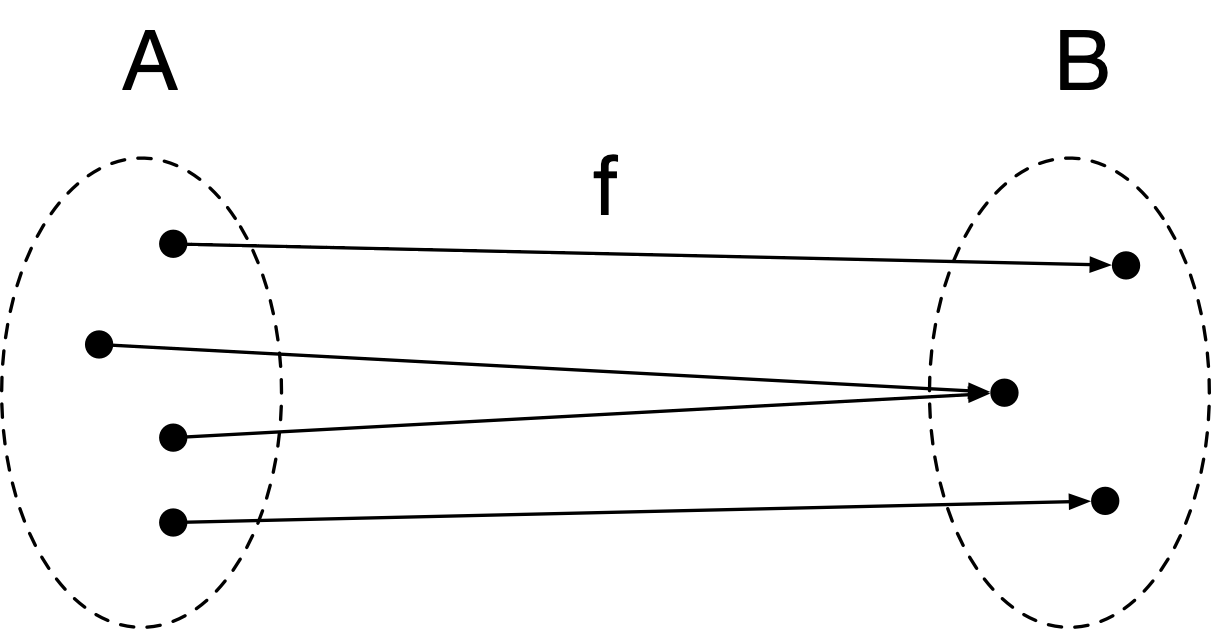
What Is Functional Programming?

  • A pure function is a total mapping between two sets
     
  • The output is determined entirely by its input.
     
  • They are mathematical functions. 

Consequences

  • Evaluating an expression always results in the same answer.
     
  • We can always inline or factor out a sub expression. Since it will yield the same result.
     
  • This property is called referential transparency 

Referential Transparency

val x = ${expr}
(x, x)
(${expr}, ${expr})

are these programs the same..?

It depends on ${expr}

Referential Transparency

val x = "hello"
(x, x)
("hello", "hello")

are these programs the same..?

Yes!

Referential Transparency

val x = println("hello")
(x, x)
(println("hello"), println("hello"))

are these programs the same..?

No!

Referential Transparency

  • Every expression is either referentially transparent or it's not.
     
  • If its not, its a side effect
     
  • If it is, its a pure expression 

Functional Programs

  • Are built using pure expressions.
     
  • Can be reasoned about using substitution.
     
  • Are composed of smaller programs.

Human Problem Solving

Human Problem Solving

  • Programs are executed on a computers CPU
     
  • However, programming languages are for humans!
     
  • So, programming languages and paradigms should
    be optimised for the human factor

Miller's Law

"the number of objects an average human can hold in short-term memory is 7 ± 2"

- Wikipedia

Miller's Law

  • This inherent limitation, is reflected in the way we solve problems.
     
  • We decompose into smaller and smaller sub-problems, until there are 7 ± 2 objects required in the
    solution.
     
  • The solutions are then composed, to solve the larger problem.

Miller's Law

  • For this to be effective in reducing our cognitive burden..
     
  • We need to be able to predict the result of composition, based on only:
    • The solutions that are being composed
    • The semantics of the composition
    • Otherwise, there can be emergent behaviour.
       
  • Reason locally about the composition

This is

Compositionality

Compositionality

"the meaning of a complex expression is determined by the meanings of its constituent expressions and the rules used to combine them."

- Wikipedia

Compositionality

  • If we have the pieces of the program that can be individually understood and we know how to glue them together then we understand the whole program.
     
  • If we can solve problems with A, B and C individually, we can solve any problem that is any combination of A, B, C.
val reader = new BufferedReader(
   new FileReader("my-file.txt")
)

var line = reader.readLine()
var count = 0

while(line != null) {
   val words = line.split("\\s")
   words.foreach { w =>
      count += 1
   }
   line = reader.readLine()
}

reader.close()
println(count)
val path = Paths.get("my-file.txt")
readAll[IO](path, blockingEc, 4096)
   .through(text.utf8Decode)
   .through(text.lines)
   .flatMap(s => Stream.emits(s.split("\\s")))
   .map(_ => 1)
   .fold(0)(_ + _)
   .evalMap(c => IO(println(c)))
val path = Paths.get("my-file.txt")
val bytes = readAll[IO](path, blockingEc, 4096)

type Transform[-A, +B] = Pipe[IO, A, B]

val words: Transform[String, String] = 
   _.flatMap(s => Stream.emits(s.split("\\s")))
   
val ones: Transform[String, Int] = 
   _.map(_ => 1)
   
val sum: Transform[Int, Int] = 
   _.fold(0)(_ + _)
   
val print: Transform[Int, Unit] = 
   _.evalMap(x => IO(println(x)))

bytes
   .through(text.utf8Decode)
   .through(text.lines)
   .through(words)
   .through(ones)
   .through(sum)
   .through(print)

val transforms: Transform[Byte, Unit] =
   text.utf8Decode[IO] andThen
   text.lines andThen
   words andThen
   ones andThen
   sum andThen
   print

bytes.through(transforms)

Functional Programming

  • Pure, mathematical functions like those used in functional programming, are compositional.
     
  • So, functional programming is really the study of compositional software.
     
  • Compositionality has massive benefits for our ability to reason about the systems we are building.

Modularity

  • Compositional programs are easily composed, and recomposed.
     
  • When requirements change and the software needs to be adpated, the compositonality makes this very easy.
     
  • In imperative systems, there are often hidden dependencies and emergent properties that require non-local reasoning to understand. This makes changes harder.

Maintainability

  • Compositional programs are easier to reason about, since they can be understood in small chunks.
     
  • When a change is required in an unfamiliar area, you can be confident that your change will only have a local impact.
     
  • A new team member can reason about a small part of the application, without needing a global understanding.

Testability

  • The meaning of our programs are defined by the meanings of the components and the meaning of the composition.
     
  • So to be confident that our software is working as expected
    • Test each of the components in isolation
    • Test that the components are assembled in the correct manner.
    • Thats it!

Summary

  • Functional programming is programming with referentially transparent functions.
     
  • Functions that are not referentially transparent, are side effects.
     
  • Referentially transparent functions are compositional
     
  • Compositionality makes it much easier for people to reason about complex programs.
     
  • Therefore, FP matters 😃

References

Why FP Matters

By Eli Jordan

Made with Slides.com

Why FP Matters

  • 922

More from Eli Jordan