First-order methods for structured optimization
Huang Fang, Department of Computer Science
Supervisor: Michael P. Friedlander
October 13th, 2021
- Optimization is everywhere: machine learning, operation research, data mining, theoretical computer science, etc.
\underset{x \in C}{\min} ~f(x)
- First-order methods:
x^{(t)} = \text{span}\{ x^{(0)}, \nabla f( x^{(0)} ), \nabla f( x^{(1)} ), \ldots, \nabla f( x^{(t-1)} ) \}
- Why first-order methods?
Background and motivation
x^{(t)}
x^{(t+1)}
The literature
- Gradient descent can be traced back to Cauchy's work in1847.
- It is gaining increasing interest in the past 3 decades due to its empirical success.
- Fundamental works have been done by pioneering researchers (Bertsekas, Nesterov, etc.).
- There are still gaps between theory and practice.
- Coordinate optimization
- Mrrior descent
- Stochastic subgradient method
Coordinate Optimization
Coordinate Descent
For
t = 0, 1, 2, \ldots,
- Select coordinate
i \in [d]
- Update
x_i^{(t+1)} = x_i^{(t)} - \eta_t \nabla_i f( x^{(t)} )
Different coordinate selection rules:
- Random selection:
- Cyclic selection:
- Random permuted cyclic (the matrix AMGM inequality conjecture is false [LL20, S20])
- Greedy selection (Gauss-Southwell)
i \in \arg\max_{ j \in [d] } | \nabla_j f( x^{(t)} ) |
i \sim \mathrm{uniform}\{1,2,\ldots, d\}
i = (t-1) ~\mathrm{mod}~ d + 1
GCD for Sparse Optimization
\underset{ x \in \mathbb{R}^d }{\min}~F(x) \coloneqq f(x) + g(x)
regularizer
- One-norm regularization or nonnegative constraint can promote a sparse solution.
- When initailzed at zero, greedy CD is observed to have an implicit screening ability to select variables that are nonzero at solution.
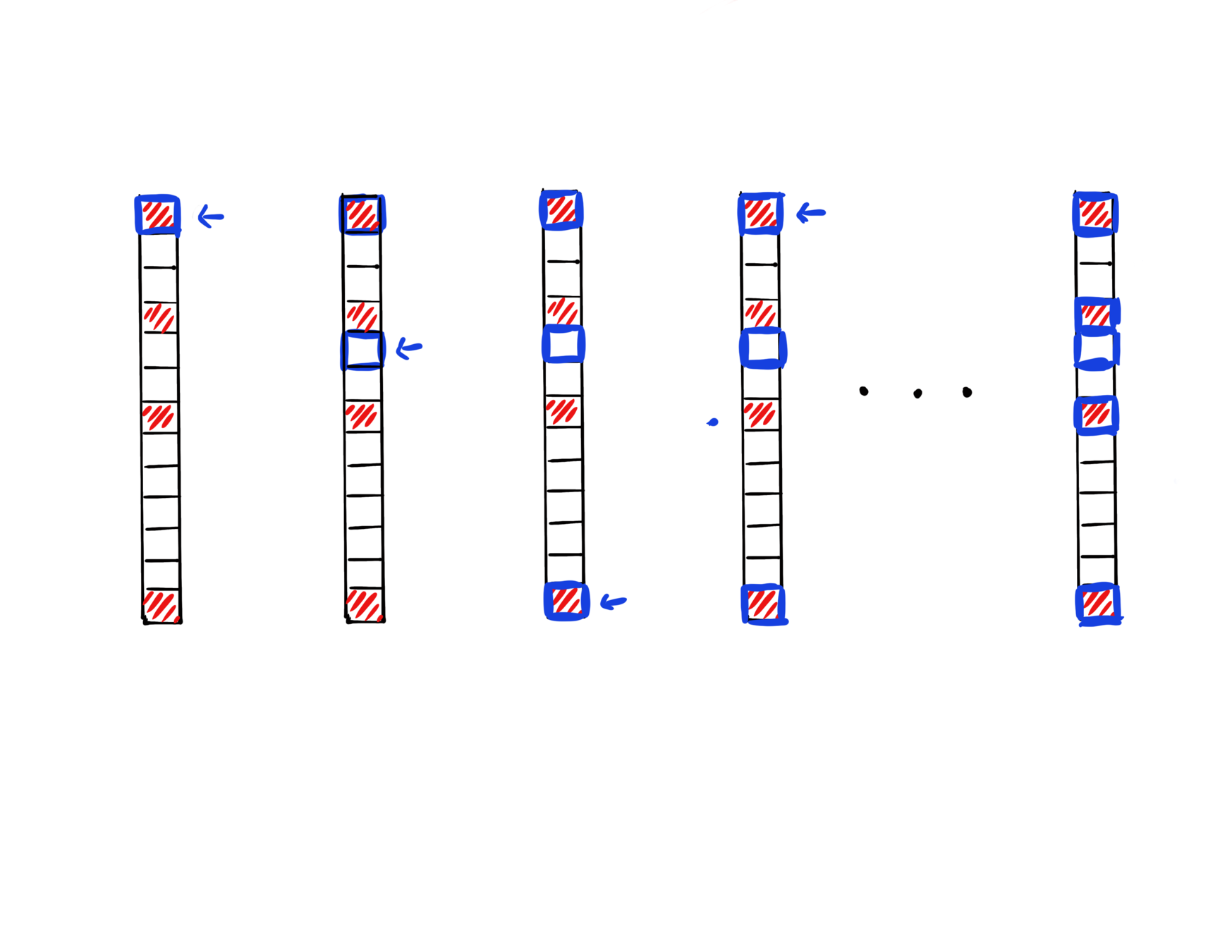
Iter 1
Iter 2
Iter 3
Iter 4
Iter
T
g(x) = \lambda \| x \|_1
g(x) = \delta_{\geq 0}(x)
data fitting
GCD for Sparse Optimization
[FFSF, AISTATS'20]
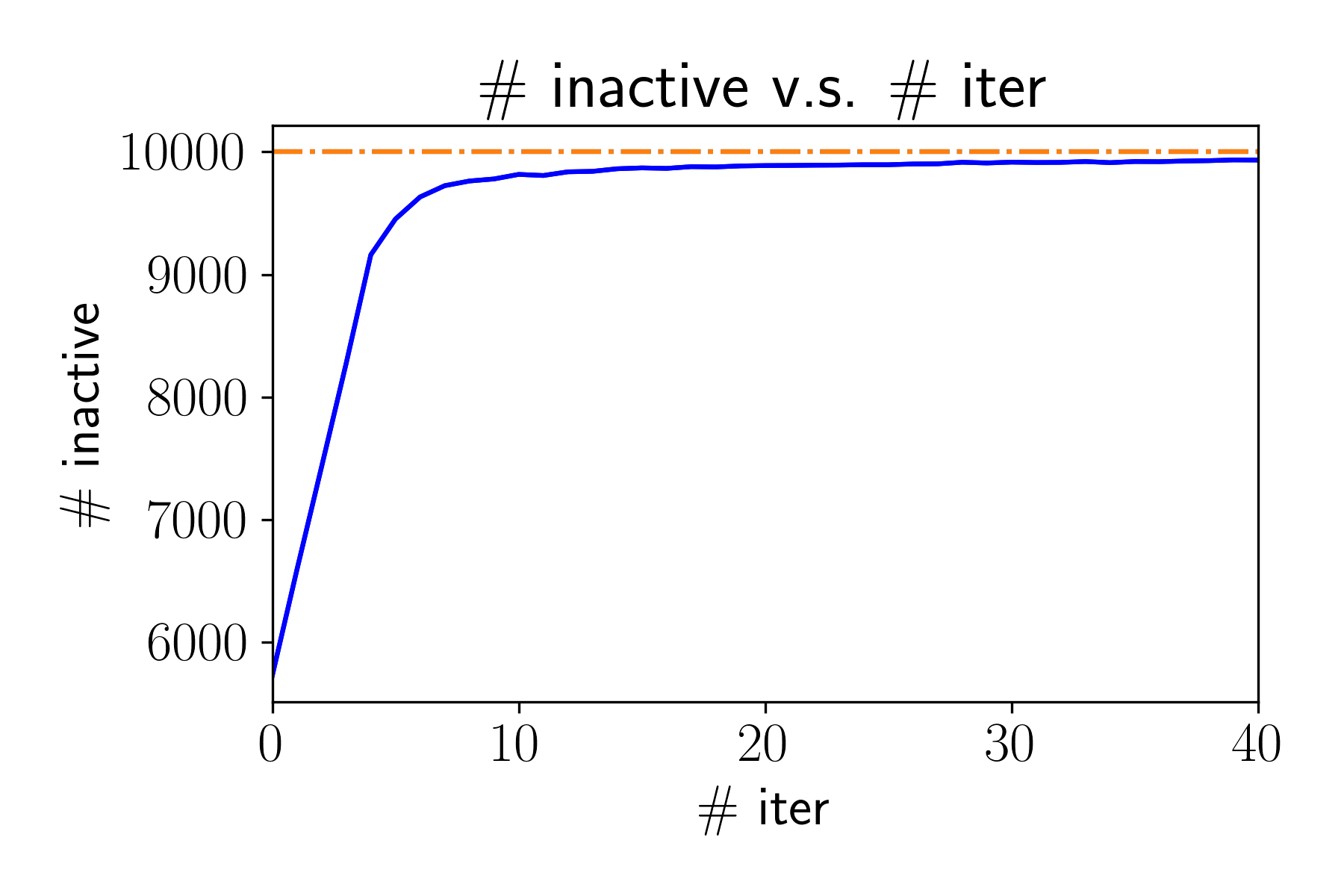
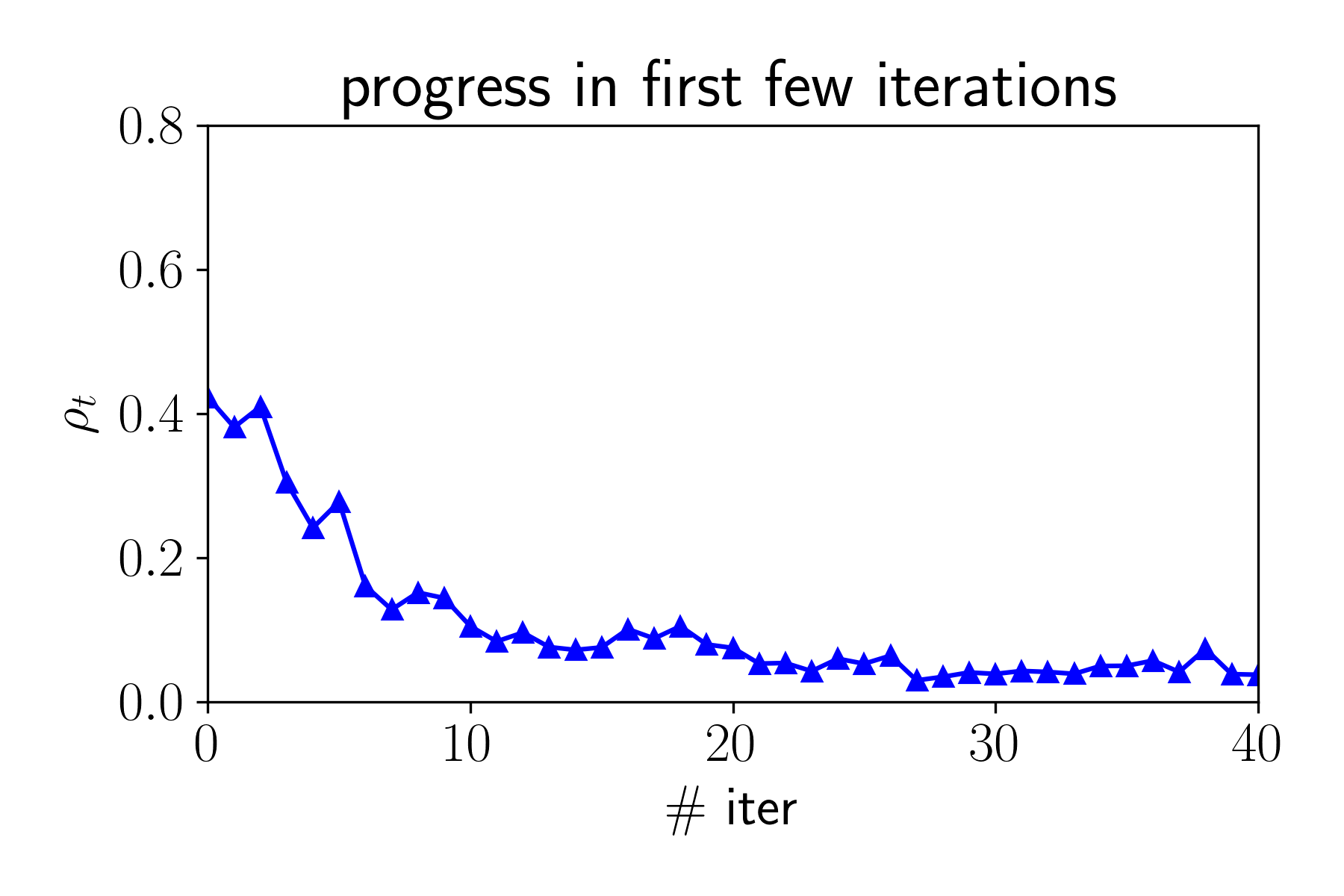
We provide a theoretical characterization of GCD's screening ability:
- GCD converges fast in first few iterations.
- The iterate is "close" the to solution when the iterate is still sparse, and sparsity pattern will not further expand anymore.
x^{(0)}
x^{*}
x^{(100)}
d = 10^4, \| x^* \|_0 = 10
\| x^{(t)} \|_0 \leq 110
for
t > 100
\delta
From coordinate to atom
Learning a sparse representation of an atomic set :
\mathcal{A}
x^* = \sum_{a \in \mathcal{A}} c_a a
such that
c_a \geq 0~\forall a \in \mathcal{A}
- sparse vector:
\mathcal{A} = \{ \pm e_1, \pm e_2, \ldots, \pm e_d \}
- Low-rank matrix:
\mathcal{A} = \{ uv^T \mid u \in \mathbb{R}^{n}, v \in \mathbb{R}^m, \|u\| = \|v\| = 1 \}
Our contribution: how to identify the atoms with nonzero coefficients at solution during the optimization process.
[FFF21] Submitted
Online Mirror Descent
Online Convex Optimization
Play a game for rounds, for
T
- Propose a point
x^{(t)} \in \mathcal{X}.
- Suffer loss
f_t( x^{(t)} ).
t = 1,2,\ldots, T
The goal of online learning algorithm: obtain sublinear regret
\displaystyle \mathrm{Regret} (T, z) \coloneqq \sum_{t=1}^T f_t( x^{(t)} ) - \sum_{t=1}^T f_t(z).
\mathrm{Regret} (T, z) = o(T) \to \mathrm{Regret} (T, z)/T \to 0.
player's loss
competitor's loss
Mirror Descent (MD) and Dual Averaging (DA)
- MD and DA are parameterized by mirror map, they have advantages over the vanilla projected subgradient method.
f_t(x) = c_t^T x \quad \text{and} \quad \mathcal{X} = \left\{ \sum_{i=1}^d x_i = 1, x_i \geq 0 \right\}, ~\|c_t\|_{\infty} \leq 1.
- When is known in advance or , both MD and DA guarantee regret
T
\mathcal{O}( \sqrt{T} ).
- When is unknown in advance and , then MD has rate while DA still guarantees regret.
T
\sup_{x, y \in \mathcal{X}} D_\Phi(x, y) = +\infty
\Omega ( T )
\mathcal{O}( \sqrt{T} )
\sup_{x, y \in \mathcal{X}} D_\Phi(x, y) < +\infty
Our contribution: fix the divergence issue of MD and obtain
regret.
\mathcal{O}( \sqrt{T} )
OMD Algorithm
[FHPF, ICML'20]
Primal
Dual
x^{(t)}
\hat{x}^{(t)}
\nabla \Phi
\hat{y}^{(t)}
-\eta_t \nabla f_t( x^{(t)} )
y^{(t)}
x^{(t+1)}
Bregman projection
\nabla \Phi^*
Figure accredited to Victor Portella
Stabilized OMD
[FHPF, ICML'20]
Primal
Dual
x^{(t)}
\hat{x}^{(t)}
\nabla \Phi
\hat{y}^{(t)}
-\eta_t \nabla f_t( x^{(t)} )
y^{(t)}
x^{(t+1)}
Bregman projection
\nabla \Phi^*
\hat{x}^{(0)}
\hat{w}^{(t)}
}
\gamma_t
With stabilization, OMD can obtain regret.
\mathcal{O}( \sqrt{T} )
(Stochastic) Subgradient Method
Smooth v.s. Nonsmooth Minimization
- Consider minimizing a convex function
- The iteration complexity of gradient descent (GD) and subgradient descent (subGD) for smooth and nonsmooth objectives:
\underset{ x \in \mathbb{R}^d }{\min}~ f(x).
- when is smooth:
f
\mathcal{O}(1/\epsilon).
- when is nonsmooth:
f
\mathcal{O}(1/\epsilon^2).
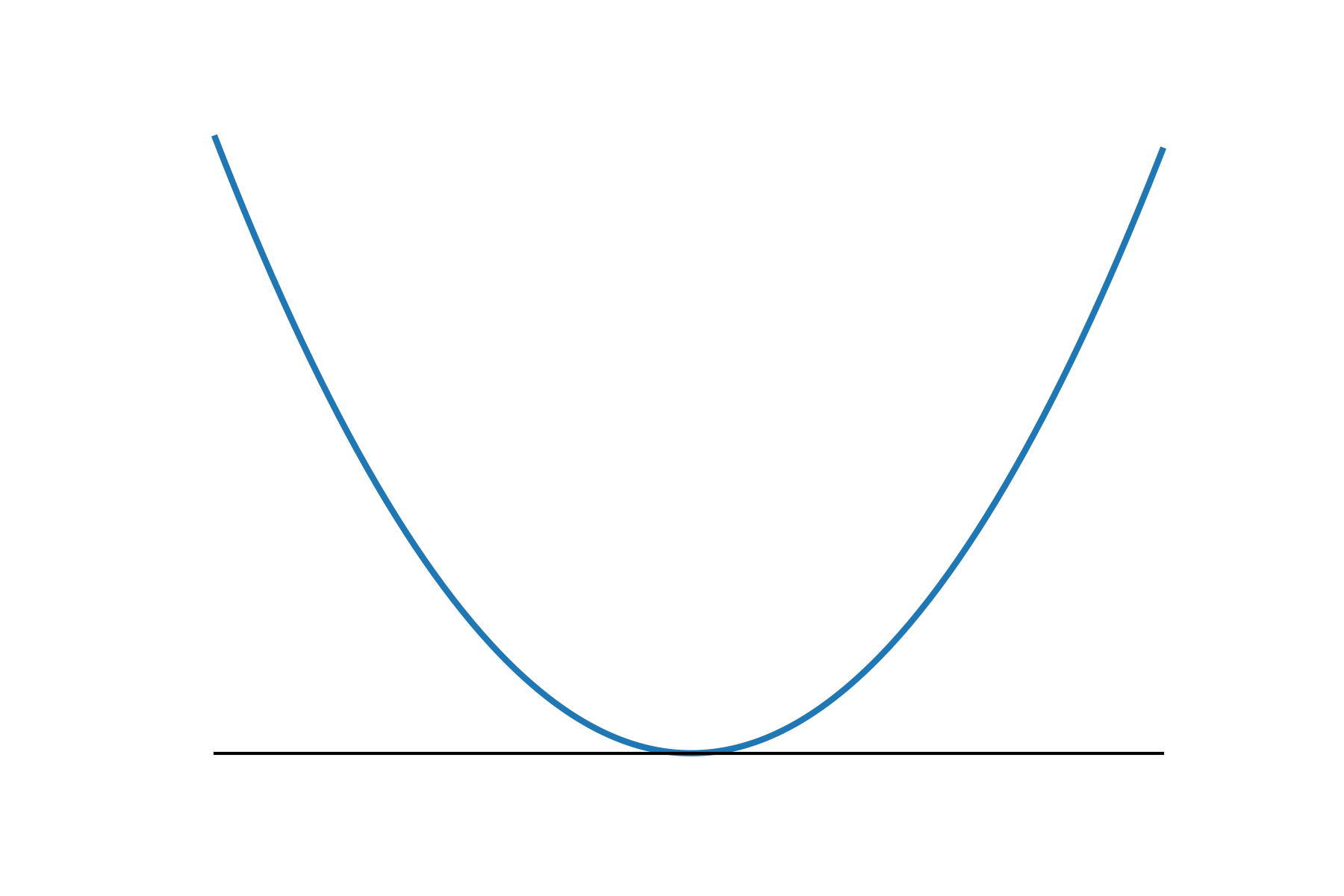
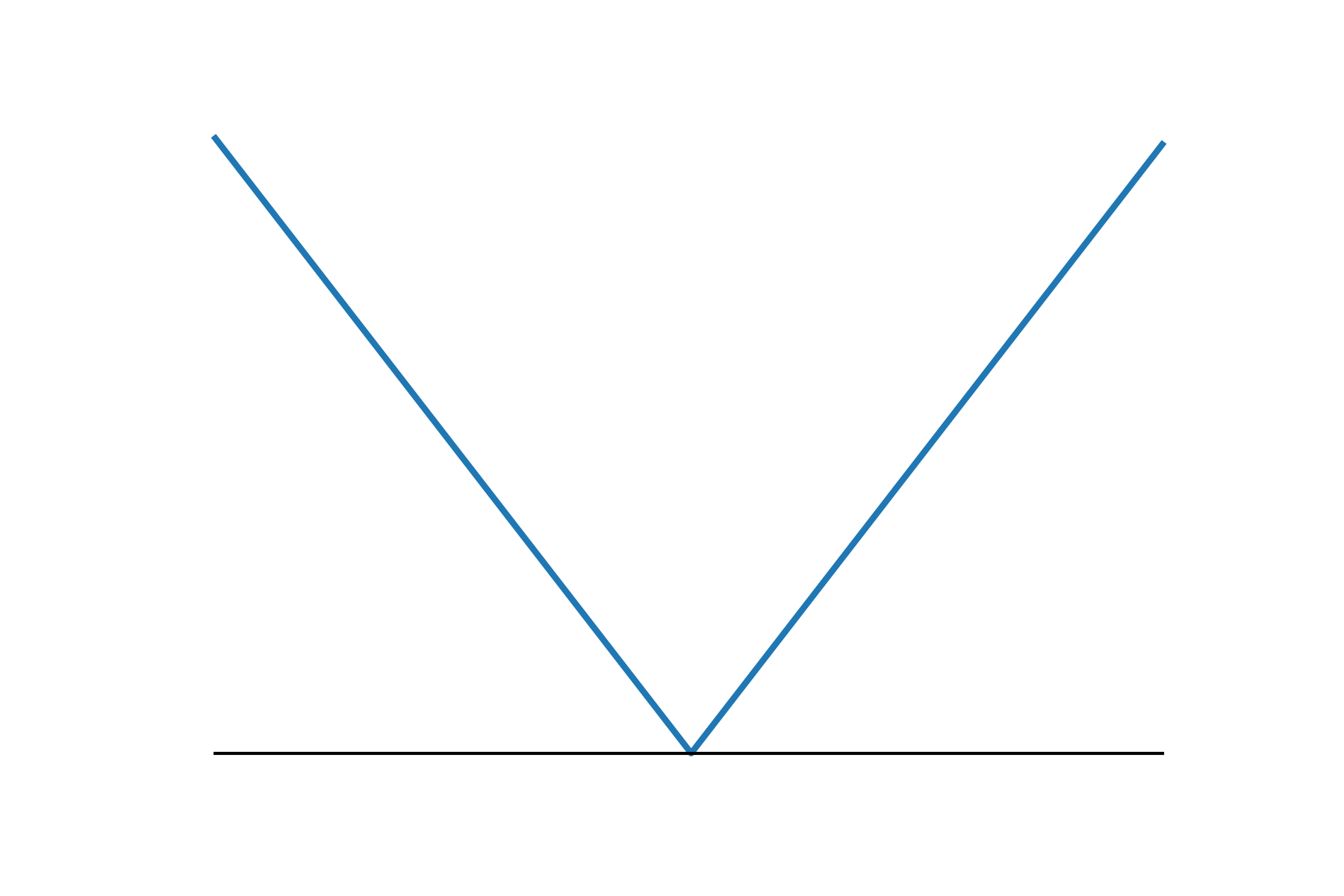
smooth
nonsmooth
The empirical observation
Some discrepancies between theory and practice:
- Nonsmoothness from the model does not slow down our training in practice.
- The learning rate schedule can yield optimal iteration complexity but seldom used in practice.
\eta_t \propto 1/\sqrt{t}
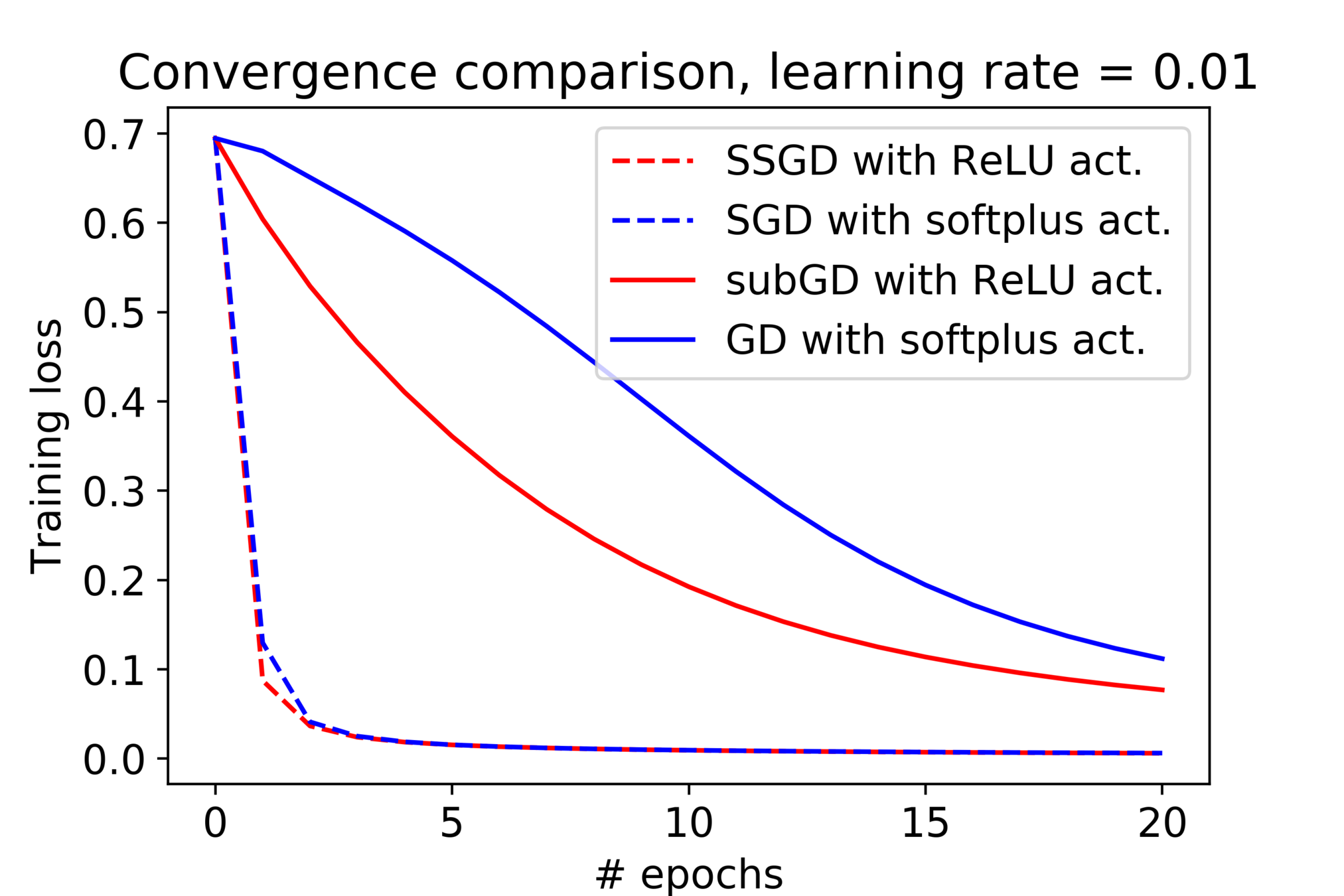
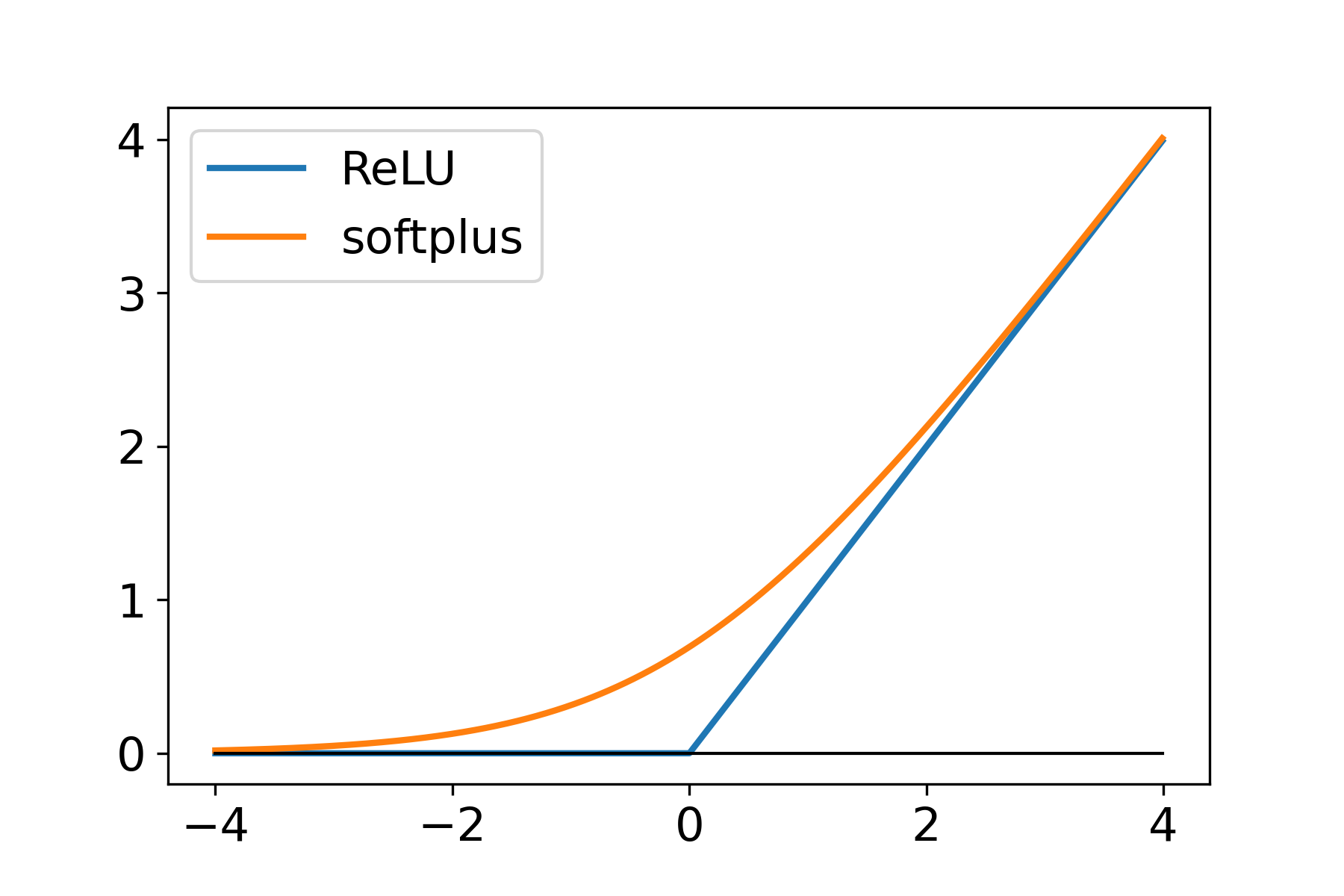
Filling the gap
Our assumption:
- The objective satisfy certain structure:
\underset{x \in \mathbb{R}^d}{\min}~ f(x) = \frac{1}{n} \sum_{i=1}^n f_i(x) \coloneqq \frac{1}{n} \sum_{i=1}^n \ell(h_i(x)),
where is a nonnegative, , convex, 1-smooth loss function, 's are Lipschitz continuous.
\ell : \mathbb{R} \to \mathbb{R}_{\geq 0}
- The interpolation condition: there exist such that
x^*
f(x^*) = 0 .
h_i
We prove
[FFF, ICLR'21]
- Convex objective:
- Strongly convex objective:
\mathcal{O}(1/\epsilon^2) \to \mathcal{O}(1/\epsilon).
\mathcal{O}(1/\epsilon) \to \mathcal{O}(\log(1/\epsilon)).
Optimal
\inf \ell = 0
- The above rates match the rate of SGD for smooth objectives.
Acknowledgment
Advisor
Committee Members
Collaborators
University Examiners
External Reviewer
Thank you! Questions?
Backup slides
Backup slides for CD
GCD for Sparse Optimization
The GS-s rule:
The GS-r rule:
The GS-q rule:
j \in \arg\max_{i \in [d]} \left\{ \min_{s \in \partial g_i(x_i)} | \nabla_i f(x) + s | \right\}
j \in \arg\max_{i \in [d]} \left\{ \left| x_i - \mathrm{prox}_{g_i/L} \left[ x_i - \frac{1}{L} \nabla_i f(x) \right] \right| \right\}
j \in \arg\max_{i \in [d]} \left\{ \min_d\left\{ \nabla_i f(x) d + \frac{Ld^2}{2} + g_i( x_i + d ) - g_i(x_i) \right\} \right\}
\displaystyle \mathrm{prox}_g (x) = \underset{y \in \mathbb{R}^d }{\arg\min}~ \frac{1}{2} \|y - x\|_2^2 + g(y)
Sparsity measure
\delta_i \coloneqq \min\{ -\nabla_i f(x^*) - l_i, u_i + \nabla_i f(x^*) \}
where .
\partial g_i(x^*_i) = [l_i, u_i]
A key property:
| \nabla_i f( x^{(t)} ) - \nabla_i f(x^*) | \leq \delta_i,~x_i^{(t)} = 0,~x_i^* = 0
\Rightarrow \quad x_i^{(t+1)} = 0
The definition of
\delta_i
\|x\|_2 \leq \| x \|_1 \leq \sqrt{d} \| x \|_2
Norm inequality:
Sparsity measure
\text{\# inactive} = \sum_{i=1}^d \textbf{1}\left\{ | \nabla_i f(x^{(t)}) - \nabla_i f(x^*) | \leq \delta_i \right\}
F( x^{(t+1)} ) - F^* = (1 - \rho_t)\left( F(x^{(t)}) - F^* \right)
Matrix AMGM inequality
\displaystyle \left\| \frac{1}{n!} \sum_{ \sigma \in \mathrm{Perm}(n) } \prod_{j=1}^n A_{\sigma(j)} \right\| \leq \displaystyle \left\| \frac{1}{n^n} \sum_{ k_1,\ldots,k_n=1 }^n \prod_{j=1}^n A_{k_j} \right\|
for all PSD matrix
A_1, \ldots, A_n \in \mathbb{R}^{d \times d}.
The matrix AMGM inequality conjecture is false [LL20, S20])
Atom identification
\mathcal{F}_\mathcal{A} ( z, \epsilon ) = \{ a \in \mathcal{A} \mid \langle a, z \rangle \geq \sigma_\mathcal{A}(z) - \epsilon \}
\mathcal{F}_\mathcal{A} ( z ) = \{ a \in \mathcal{A} \mid \langle a, z \rangle \geq \sigma_\mathcal{A}(z) \}
where is the support function.
\sigma_{\mathcal{A}}(z) = \sup_{a \in \mathcal{A}} \langle a, z \rangle
x \to x^* \quad {\Rightarrow} \quad \mathrm{supp}(x) \to \mathrm{supp}(x^*)
y \to y^* \quad \Rightarrow \quad \mathcal{F}_{\mathcal{A}}(y, \epsilon) \to \mathcal{F}_{\mathcal{A}}(y^*)
The primal-dual relationship:
\mathrm{supp}(x^*) \subseteq \mathcal{F}_{\mathcal{A}}(y^*)
This allows us to do screening base on dual variable:
Backup slides for OMD
Basics
Bregman divergence
D_\Phi(x, y) \coloneqq \Phi(x) - \Phi(y) - \langle \nabla \Phi(y), x - y \rangle
Properties of mirror map
\Phi : \bar{\mathcal{D}} \to \mathbb{R}^d
- is nonempty,
\mathcal{D}
- is differentiable on , and
\Phi
\mathcal{D}
- , where is the boundary of , i.e.,
\partial \mathcal{D}
\lim_{x \to \partial \mathcal{D}} \| \nabla \Phi(x) \| = + \infty
\mathcal{D}
\partial \mathcal{D} \coloneqq \mathrm{cl} \mathcal{D} ~\backslash~ \mathcal{D}.
\Phi(x) = \frac{1}{2} \| x \|_2^2 ~\Rightarrow~ D_\Phi(x, y) = \frac{1}{2} \| x - y \|_2^2
Examples:
\Phi(x) = \sum_{i=1}^d x_i \log(x_i) ~\Rightarrow~ D_\Phi(x, y) = \sum_{i=1}^d x_i \log(x_i/y_i)
Backup slides for SGD
Basics
| smooth | nonsmooth | smooth+IC | nonsmooth + IC | |
|---|---|---|---|---|
| convex | ||||
| strong cvx |
\mathcal{O}(1/\epsilon)
\mathcal{O}(1/\epsilon^2)
\mathcal{O}(1/\epsilon^2)
\mathcal{O}(1/\epsilon)
\mathcal{O}(1/\epsilon)
\mathcal{O}(\log(1/\epsilon))
\mathcal{O}(1/\epsilon^2)
\mathcal{O}(1/\epsilon)
Semi-smooth properties
Assume , is -Lipschitz continuous and is nonnegative, convex, 1-smooth, minimum at 0, 1-dimensional function. Then
f(x) \coloneqq \ell( h(x) )
h
L
\ell
\| \partial f(x) \|^2 \leq 2 L^2 f(x)
(the generalized growth condition)
\| \partial f(x) - \partial f(y) \| \leq L^2 \| x - y \| + 2L \sqrt{2\min\{ f(x), f(y) \}}
Extension
High probability error bound
\mathcal{O}( \log(1/\delta)/\epsilon )
Conjecture: variance reduced SGD (SAG, SVRG, SAGA) + generalized Freedman inequality
\to
Simple proof of exponential tail bound
thesis
By Fang Huang
thesis
Slides for my oral defense
