Fixing software with pure functional programming
- Purity — Functions map inputs to outputs and do nothing else.
- Total functions — Functions are well-defined for every input.
- Laziness — Values are computed on-demand.
- Immutability — Values do not change once created.
- Expressive data — Expressive data, free from behavior
- First class Functions — Functions all the way down
- Strong type system — Solve the problem at the type-level
Why pure functional programming?
Purity
Purity - what is it?
That means absolutely no I/O!
- No talking to the "real world"
- No mutation of state that escapes local scope
- No input, just data
A pure function is simply a mapping from one value to another value.
function evilSqrt(n: number): number {
launchMissles();
}Purity - what is it?
Deterministic
- Same input yields same output
- Function becomes a mere table lookup
- Removes guess work as to what a function does
- REPL friendly
- The equal sign actually means equality
- Equal values can be substituted at any time
- Extracting functions becomes easy
- Value-level equality, no concept of "references"
Purity - what is it?
No runtime exceptions
- Pure code has no concept of exceptions
- Errors are encoded as types, for example Either Error a
- Compiler enforced freedom from exceptions
Purity - what is it?
Efficient
- Because the compiler knows there's no I/O, it can optimize:
- Structural sharing
- Stream fusion
-- option 3) nice and efficient code
take 5 (filter odd [1..])// option 1) nice code, but expensive
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10].filter(isOdd).slice(0, 5);// option 2) ugly code, but efficient
var out = [];
for (var i = 0; i < xs.length; i++) {
if (isOdd(xs[i])) {
out.push(xs[i]);
}
}
return out;Stream fusion example: take first `n` elements that pass filter
Purity - Quiz
Q: Would you consider this function pure?
function sumEvens (n) {
var x = 0;
for (var i = 0; i <= n; i++) {
if (i % 2 == 0) {
x++;
}
}
return x;
}A: Yes, because mutations are isolated
Purity - Quiz
Q: How about this function, is it pure?
var messages = [];
function addMessage (message) {
messages.push(message);
}A: No, it mutates state out of it's scope
Q: How about this one?
var messages = [];
var addMessage = messages.push.bind(messages);A: No, same reason applies
Purity - Quiz
Q: Then, how about this one, is it pure?
function checkTime(time) {
if (Date.now() > time) {
return "it's the future";
else if (Date.now() === time) {
return "it's the present";
} else {
return "it's the past";
}
}A: Nope, "Date.now" has to do I/O to get the current time
Purity - Quiz
Q: Now, is this one pure?
var uuid = require('uuid');
function getId() {
return uuid.v4();
}A: Nope, uuid has to use some RNG internally to provide the random uuids, which in turn would require I/O again.
Purity - Quiz
Q: One more, is this one pure?
const users = [];
function getUsers(request: { take?: number, skip?: number }): boolean {
request.take = request.take == null ? 10 : request.take;
request.skip = request.skip == null ? 0 : request.skip;
return users.slice(request.take, request.skip);
}A: Nope, because we're mutating the input!
Purity
So what if we could remove the guess-work by assuming purity?
mystery :: ∀ a. a -> afunction name
type of output
type of input
type variables
mystery x = ???function body
mystery x = xTotal vs. Partial functions
aka "undefined is not a function"
Total vs. partial functions
We realize there are two kinds of functions
- Total functions — well-defined output on every point (input)
- Partial functions — defined only for a subset of points (inputs)
Example:
function toString(x: any): string {
return x.toString();
}
> toString(undefined)
TypeError: Cannot read property 'toString' of undefined> toString(undefined)Total vs. partial functions
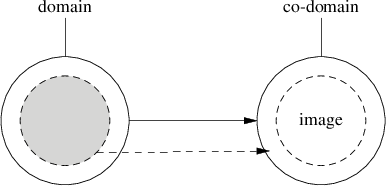
A function maps values in it's domain to values in it's co-domain (or a subset called the image). If for any point in domain there's no point in it's co-domain, the function is considered partial.
Total vs. partial functions
- Every type is inhabited with a potentially infinite amount of values.
- For example, the values 1, 2, 3, ... all inhabit the number type in e.g. typescript
- But in Javascript and other weakly typed languages, all values inhibit every type
- Worse yet, null and undefined also inhabit every type
- For a function to be total, all values that inhabit the input type, must have a corresponding value in the output type
Types and inhabitants:
Total vs. partial functions
Therefore, every value must be treated as nullable and checked
type Account = { id: string
, firstName?: string
, lastName?: string
, clients: { id: string }[]
}
function isProfessionalOf(account: Account, clientId: string): boolean {
if (account != null) {
if (account.clients != null) {
if (Array.isArray(account.clients) {
// ...
} else {
??? // no sensible output in co-domain
}
} else {
??? // no sensible output in co-domain
}
} else {
??? // no sensible output in co-domain
}
}...but that is prone to errors as well and no one does it...
Total vs. partial functions
So, what if we could remove "null" and "undefined" from every type?
type Account = { id: string
, firstName?: string
, lastName?: string
, clients: { id: string }[]
}
function isProfessionalOf(account: Account, clientId: string): boolean {
return account.clients.indexOf(clientId) >= 0;
}...suddenly, our code cannot crash anymore and we are guaranteed meaningful output...
Total functions - Quiz
Q: Is the following function partial or total?
head :: ∀ a. [a] -> aA: It is partial as we cannot produce an a when the list is empty:
head :: ∀ a. [a] -> a
head (x:_) = x
head [] = ???A total function on the other hand is defined for all points. This requires us to encode the possible lack of an "a" at the type level.
head :: ∀ a. [a] -> Maybe a -- `Maybe a` is a civilized `null`
head (x:_) = Just x
head [] = NothingTotal functions - Quiz
Q: Is the following function partial or total?
divide :: Int -> Int -> IntA: It is partial as we cannot divide by 0!
Again, a more sensible approach would be to convey this in the types:
divide :: Int -> Int -> Maybe Int
divide _ 0 = Nothing
divide x y = x `div` yLaziness
Let the compiler figure it out
Laziness
Defer computations until they become necessary and let the runtime worry about when and how to evaluate.
-- Example:
-- Define the set of all even natural numbers but only force the
-- first 50 values into existence:
main =
let nats = [x | x <- [1..], even x]
in traverse print $ take 50 natsNotes about Laziness:
- Requires support by the runtime
- It can be hard to understand space / time complexity
- New kinds of bugs: Space / time leaks
- Lazy I/O is a cool idea, but also dangerous
Immutability
Immutability - what is it?
Values cannot be changed once created.
- Data runs strictly down the program
- Values can be modified by creating modified copies
- Efficient thanks to structural sharing
- Mutable state can be modeled using I/O
- Compiler enforced
- Impossible to accidentally modify
let x = Map.empty
x' = Map.insert "hundred" 100 x
x `shouldEqual` Map.empty
x' `shouldEqual` (Map.insert "hundred" 100 (Map.empty))Immutability - why care?
Immutability has several interesting advantages to mutability
- Naturally scales across threads, network, etc.
- We rely on "extensional" equality (as opposed to "intensional"). That is equality by value. No need to track references. References only exist in memory, but our computations could take place elsewhere.
- Compiler-enforced guarantees about correctness
- Removes many bugs from the system
- It removes a huge cognitive burden when reading code
Immutability - civilized mutable state
Sometimes, however, mutable state is necessary. We provide "civilized" access to such state
main :: IO ()
main = do
ref <- newIORef 0
_ <- modifyIORef ref (+1)
v <- readIORef ref
print v -- prints "1"Expressive data
products: data Tuple = Tuple a b
and sums: data Either a = Left a | Right b
Expressive data - overview
- Algebraic data - sums and products
-
Polymorphism
- Keep data structure general
- And specialize via functions
- Type classes
- Declare membership at site of data definition
- Or declare membership at site of class definition
- Or elsewhere (orphan instances)
-
Recursive
-
data List = Cons a | NilData - Products and sums
Product types
data TwoInts = TwoInts Int Int
myInts :: TwoInts
myInts = TwoInts 10 20Sum types
data MaybeInt
= YesInt Int
| NoInt
x :: MaybeInt
x = YesInt 100
y :: MaybeInt
y = NoIntMultiple mutually exclusive "constructors" under a common type, where each constructor can again be a sum or product type
A single constructor compromised of 0-n values
Data - Products
data Account = Account { id :: String
, firstName :: String
, lastName :: String
}data TwoInts = TwoInts Int IntCompound data types allow us to pack multiple values into a single value
The compounded values can also be labeled
The total number of values in the type is the product of the number of values in each compounded type. More on that later
Data - Sums
data MaybeInt = YesInt Int | NoIntUnion of mutually exclusive constructors
The "|" means "OR"
Essentially, we get enums with associated values:
let hasInt = case value of
YesInt v -> true -- `v` is bound to the `Int` inside `YesInt`
NoInt -> false -- otherwise, well, there's no valueThe total number of values in this type is the sum of the total number of values in each constructor. More on that later.
Data - Polymorphism
data TwoInts = TwoInts Int Int
myInts :: TwoInts
myInts = TwoInts 10 20data Tuple a b = Tuple a bmyInts :: Tuple Int Int
myInts = TwoInts 10 20generalized data structures
and specialized functions
Data - Polymorphism
Maybe a = Just a | Nothing}
This type can be used for any "a". The structure does not change based on which "a" we choose.
This is called a "type constructor". To create an actual type, we apply the type constructor to another type:
type MaybeInt = Maybe IntData - Trivia
data Unit = Unit
-- total values: 1
data Maybe a = Just a | Nothing
-- total values: a + 1
data Either a b = Left a | Right b
-- total values: a + b
data Tuple a b = Tuple a b
-- total values: a * b
data ColorMode = RGB | GrayScale
-- total values: 1 + 1 = 2
data SamplingMode = NearestNeighbour | Bilinear | Trilinear
-- total values: 1 + 1 + 1 = 3
data Config = Config { colorMode :: ColorMode, sampling :: SamplingMode }
-- total values: 2 * 3 = 6A: Because that's how we calculate the total amount of inhabitants in a type!
Q: Why is it called product and sum types?
Type classes
Akin to "Interfaces" from OOP, but actually practical to use
- We can declare a type class instance at any point
- Declare one alongside the data type definition
- Declare one alongside the class definition
- We can require a type to implement a type class in function types
- We can declare a type class depend on another type class
- We can provide default implementations
- We can even provide default implementations in terms of other default implementations
Type classes Example
class Semigroup a where
append :: a -> a -> a
class Semigroup a <= Monoid a where
mempty :: ainstance Monoid String where
mempty = ""
instance Semigroup String where
append a b = a + bLet's make "String" an instance of both classes
Let's make a function that works on any "Monoid"
mconcat :: ∀ a. Monoid a => Array a -> a
mconcat xs = foldl append mempty xs> mconcat [ "a", "b", "c" ]
"abc"Let's define two type classes
Functions
The bread and butter
Functions - Overview
- Compiler checked totality
- Compiler checked purity
- Composable and substitutable
- Type-level functions vs. value-level functions
- Visually lightweight
- Whitespace is function application
- "point-free" style via eta-reduction
- Currying and partial application
- Combinators - functions that only refers to it's arguments
Functions - Currying
- Functions always only take one argument
- To group inputs, you would use a Tuple
- To return "multiple values", you return a Tuple
- "Curried" as in Haskell Curry, American mathematician and logician who paved the path towards Haskell
/*
* Curried functions only take one argument at a time.
*
* take :: ∀ a. Int -> ([a] -> [a])
*/
function take(amount) {
return function(array) {
return array.slice(0, amount)
}
}> var take3 = take(3); /* take3 :: ∀ a. [a] -> [a] */
> console.log(take3([1, 2, 3, 4, 5, 6, 7, 8, 9]))
[1, 2, 3]Functions - Recursion
How do you write a loop without "while" and "for" builtins?
Recursion comes naturally and has us think about the "edge cases" first, to ensure termination
take :: Int -> [a] -> [a]take _ [] = [] -- nothing more to take!take n _ | n <= 0 = [] -- nothing more to take!take n (x:xs) = x : take (n - 1) xs -- take this `x` and take `n - 1` moreWe recurse towards the edge case
Functions - Recursion
Why would we want to get rid of builtin looping constructs?
- Define values at points (declarative programming)
- Since functions are expressions, recursion is composable
- We focus on the true (or "essential") complexity of the problem
- Avoid mutation
Functions - Tail recursion
Tail recursion allows us to pop the stack before recursing because we don't need to come back to it.
take :: ∀ a. Int -> [a] -> [a]
take _ [] = []
take n _ | n <= 0 = []
take n (x:xs) = x : take (n - 1) xs -- <<<take :: ∀ a. Int -> [a] -> [a]
take n xs = go n xs []
where go _ [] acc = acc
go n _ acc | n <= 0 = acc
go n (x:xs) acc = go (n - 1) xs (acc <> [x])"x" remains on the stack, in order to apply the append function "(:)" later after "take" stops recursing
By manually threading the accumulator, we can elide the
stack and operate on a single stack frame
Functions - Tail recursion
- Only an issue in strictly evaluated languages
- To do this day, Javascript and other popular languages do not support this
- Tail recursive functions can always be transformed into while loops
Functions - Recursive patterns
- Manual recursion can be error-prone
- Recursive functions often look structurally similar
- We can generalize!
- Finding common patterns and extracting is very common, easy and encouraged
sum :: [Int] -> Int
sum xs = go 0 xs
where go acc [] = acc
go acc (x:xs) = go (acc + x) xssum :: [Int] -> Int
sum xs = foldl (+) 0 xsCase in point: Folds
}
Functions - Recursive patterns
- Manual recursion can be error-prone
- Recursive functions often look structurally similar
- We can generalize!
- Finding common patterns and extracting is very common, easy and encouraged
sum :: [Int] -> Int
sum xs = go 0 xs
where go acc [] = acc
go acc (x:xs) = go (acc + x) xssum :: [Int] -> Int
sum xs = foldl (+) 0 xsCase in point: Folds
}
Functions
are composable
Function composition
B
A
C
g
f
f o g
- Given a function "g", from A to C
- And a function "f", from B to C
- We can produce a function "f . g" from A to C
Function composition
So, why would one care for that?
We can quickly build functions from functions:
> filter (not . isSuffixOf "@sylo.io" . map toLower . snd)
> [ (1, "ben@sylo.io")
> , (2, "rick@gmail.com")
> , (3, "scott@sylo.io") ]
>
[ "rick@gmail.com" ]- It costs nothing
- It reduces likelihood of errors
- There is no unnecessary clutter
- It encourages point-free style programming (up next)
Functions
Point-free style programming
Functions - point-free
Often functions can be given in "point free" style. Point free programming means to omit the explit argument to a function definition, if the last thing the function body does is function application.
doubleAll :: [Int] -> [Int]
doubleAll xs = map (\x -> x * 2) xsdoubleAll = map (\x -> x * 2)doubleAll = map (* 2)Functions - point-free
On a side-note, this is what makes bash pipelining so powerful!
# quickly switch to a different tmux session using FZF
tmux_select_session () (
set -eo pipefail
local -r prompt=$1
local -r fmt='#{session_id}:|#S|(#{session_attached} attached)'
{ tmux display-message -p -F "$fmt" && tmux list-sessions -F "$fmt"; } \
| awk '!seen[$1]++' \
| column -t -s'|' \
| fzf -q'$' --reverse --prompt "$prompt> " \
| cut -d':' -f1
)
Control flow
>>=
Control flow
Have you ever wondered...
function main () {
console.log("foo");
// <- ... what happens here ???
console.log("bar");
}In functional programming, the answer is clear:
main :: IO ()
main =
putStrLn "foo" >>= \_ -> -- function application, of course!
putStrLn "bar"Or, using syntactic sugar ("do-syntax"):
main :: IO ()
main = do
putStrLn "foo"
putStrLn "bar"Control flow
Being able to control what happens in-between statements is where all the magic comes together.
The ">>=" (or "bind") function lives in the "Monad" type-class. Therefore, the "statement glue" differs from each
type to type
type Host = String
type DbName = String
data DbSettings = DbSettings Host DbName
getDbSettings
:: Map String String
-> Maybe DbSettings
getDbSettings = do
dbHost <- Map.lookup "DB_HOST" env
dbName <- Map.lookup "DB_NAME" env
Just $ DbSettings dbHost dbNameAn example of the "Maybe" monad
getDbSettingsA
:: Map String String
-> Maybe DbSettings
getDbSettingsA
= DbSettings
<$> (Map.lookup "DB_HOST" env)
<*> (Map.lookup "DB_NAME" env)"Applicative" style, allows for parallelisation
Control flow examples
Global, immutable configuration made safe and easy using the "Reader" monad.
import Control.Monad.Trans.Reader (ReaderT, runReaderT)
import Control.Monad.Reader as Reader
someComputation :: ReaderT Config IO ()
someComputation = do
config <- Reader.ask
lift $ print $ config
main :: IO ()
main = runReaderT someComputation =<< loadConfigFromDiskAn example of the "Reader" monad
Control flow examples
Mimicking thread-local state is easy, using the "State" monad. Note that state remains immutable!
import Control.Monad.State (State, runState)
import Control.Monad.State as State
increment :: State Int
increment = State.modify (+ 1)
decrement :: State Int
decrement = State.modify (- 1)
main :: IO ()
main = do
print $
execState 1 $ do
increment -- + 1 (state is now 2)
increment -- + 1 (state is now 3)
decrement -- - 1 (state is now 2)
increment -- + 1 (state is now 3)An example of the "State" monad
Control flow examples
deleteUsers
:: MonadIO m
=> [UserId]
-> ReaderT SqlBackend m Int64
deleteUsers ids = do
E.deleteCount $
E.from $ \user -> do
E.where_ (user E.^. UserId `E.in_` E.valList ids)Now, to finish off, imagine type-safe access to your database in an easy to read, refactor, compose and extract EDSL.
It's possible!
Closing thoughts
- Drastically reduces number of bugs
- You end up writing and hence maintaining less code
- Removes accidental complexities. Focus on what's essential
- Very easy to refactor code (extracting functions etc.)
- I found it easier to read and understand other people's code
- Learning functional programming is extremely enlightening, even outside the computer
- To get into it, you have to accept that almost none of the concepts you know of already will apply... Trying to bring them over is going to slow you down. Consider it a sort of rebirth.
And that's it
http://learnyouahaskell.com/
https://leanpub.com/purescript/read
Fixing software with pure functional programming
By felixschl
Fixing software with pure functional programming
- 906
