(the back-and-forth method)
A fast approach to optimal transport
Flavien Léger
Joint work with Matt Jacobs (UCLA)
Our interests
We have in mind PDE-type applications:
2D or 3D, up to 100 million points,
continuous density on regular grids.
Computational OT
- Linear programming
- Monge–Ampère solvers
- Entropic regularization (Sinkhorn)
- Benamou–Brenier
- Semi-discrete
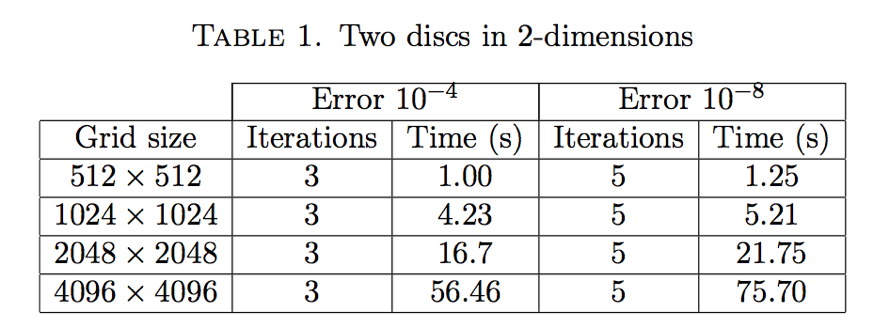
Back-and-forth: up to 100 million points
Kantorovich dual
$$\sup_{\phi,\psi} \int_{\Omega} \phi(y)\,\nu(dy) - \int_{\Omega}\psi(x)\,\mu(dx)$$
s.t. \( \quad \phi(y) - \psi(x) \le c(x,y)\)
If \((\phi, \psi)\) is a solution pair to the dual problem then
\begin{aligned}
\psi(x)=\phi^c(x):=\sup_{y\in\Omega} \, \phi(y)-c(x,y) \\
\phi(y)=\psi^c(y):=\inf_{x\in\Omega} \, \psi(x)+c(x,y)
\end{aligned}
Two dual functionals
$$J(\phi)= \int_{\Omega} \phi(y)\,\nu(dy)-\int_{\Omega} \phi^c(x)\,\mu(dx)$$
$$I(\psi)= \int_{\Omega} \psi^c(y)\,\nu(dy)-\int_{\Omega} \psi(x)\,\mu(dx)$$
The \(c\)-transform and maps
From now on assume \(c(x,y)=h(y-x)\) for \(h\) strictly convex.
Define:
$$T_{\phi}(x)=\arg\max_y \phi(y)-h(y-x).$$
We have
$$T_{\phi}(x)=x+(\nabla h)^{-1}(\nabla\phi^c(x)).$$
\(c\)-transform variation
Recall
$$T_{\phi}(x)=\arg \max_{y} \phi(y)-h(y-x).$$
Then
$$(\phi + \epsilon u)^c(x) = \phi^c(x) + \epsilon \, u(T_{\phi}(x))+o(\epsilon)$$
(Gangbo–McCann '96)
Recall that \(J(\phi)=\int\phi\,d\nu-\int \phi^c\,d\mu\).
First variation:
$$\delta J(\phi)u=\int u\, d(\nu-T_{\phi\, \#}\mu)$$
The back-and-forth method
\phi_{n+\frac{1}{2}}=\phi_n+\sigma \nabla_{\!H}J(\phi_n)
\psi_{n+\frac{1}{2}}=\psi_n+\sigma \nabla_{\!H}I(\psi_n)
Fundamental lemma of optimization
If \(F\colon H\to\mathbb{R}\) is a concave functional that satisfies
$$\lVert \delta F(\phi_2)-\delta F(\phi_1)\rVert _{H^*} \le L\lVert \phi_2-\phi_1\rVert_H$$
for any \((\phi_1,\phi_2)\in H\) then the iterations
$$\phi_{n+1}=\phi_n+\frac{1}{L}\nabla_{\!H} F(\phi_n)$$
converge to the supremum of \(F\).
Back-and-forth is fast
\begin{aligned}
\phi_{n+\frac{1}{2}}&=\phi_n+\sigma(-\Delta)^{-1}(\nu-T_{\phi_n\#}\mu) \\
\psi_{n+\frac{1}{2}}&=(\phi_{n+\frac{1}{2}})^c
\end{aligned}
Operations on a grid with \(N\) points:
- \(c\)-transform: \(O(N\ln N)\)
- \(T_{\phi_n} : O(N\ln N) \)
- \(\Delta^{-1}:O(N\ln N)\)
Numerical Experiments
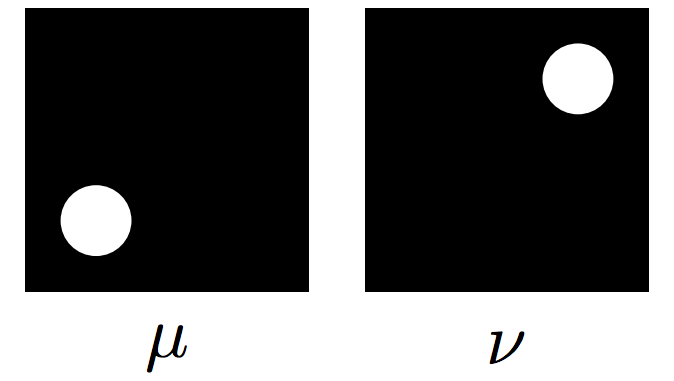
Movies!
Caffarelli's counterexample
Santambrogio–Wang's convexity counterexample
Rectangles
\(\mu\)
\(\nu\)
Monge map \(T\)
Wasserstein gradient flows
(WIP with Matt Jacobs and Wonjun Lee (UCLA))
\(W_2\) gradient flows
\begin{cases}
\partial_t\rho+\mathrm{div}(\rho\nabla\phi)=0 \\
\phi=-\delta E(\rho)
\end{cases}
Consider a functional \(E(\rho)\) and the PDE
Example
$$E(\rho)=\frac{1}{m-1}\int \rho^m+\int V\rho$$
Then: porous medium equation
$$\partial_t\rho+\mathrm{div}(\rho(-\nabla V))=\Delta\rho^m$$
(Otto '01)
JKO scheme
$$\mu^{k+1}=\arg\min_{\rho} E(\rho)+\frac{1}{2\tau}W_2^2(\mu^k,\rho) .$$
Dual problem:
$$\sup_\phi -E^*(-\phi)-\int \phi^c \,d\mu^k.$$
(compare to:
$$\sup_\phi \int\phi\,d\nu-\int \phi^c \,d\mu.$$)
(J–K–O '98)
Movies!
$$E(\rho)=\int \rho\ln\rho + \int V\,\rho$$
with
V(x)=\begin{cases} \infty\quad\text{if } x\in D \\ \lvert x\rvert^2/2 \quad\text{otherwise}\end{cases}
Slow diffusion
Slow diffusion
\displaystyle E(\rho)=\int \rho^m+\int \lvert x\rvert^2\rho
m=2
m=4
Thank you!
The back-and-forth method
By Flavien Léger
