Gradient descent with a general cost
Flavien Léger
joint works with Pierre-Cyril Aubin-Frankowski
1. A new family of algorithms
2. Convergence theory
3. Applications
Outline
Gradient descent as alternating minimization
General method unifies gradient/mirror/natural gradient/Riemannian descent
Generalized smoothness and convexity
Optimal transport theory → local characterizations
Global rates for Newton
Explicit vs. implicit Riemannian gradient descent
1. Gradient descent as minimizing movement
Two steps:
1) majorize: find the tangent parabola (“surrogate”)
2) minimize: minimize the surrogate
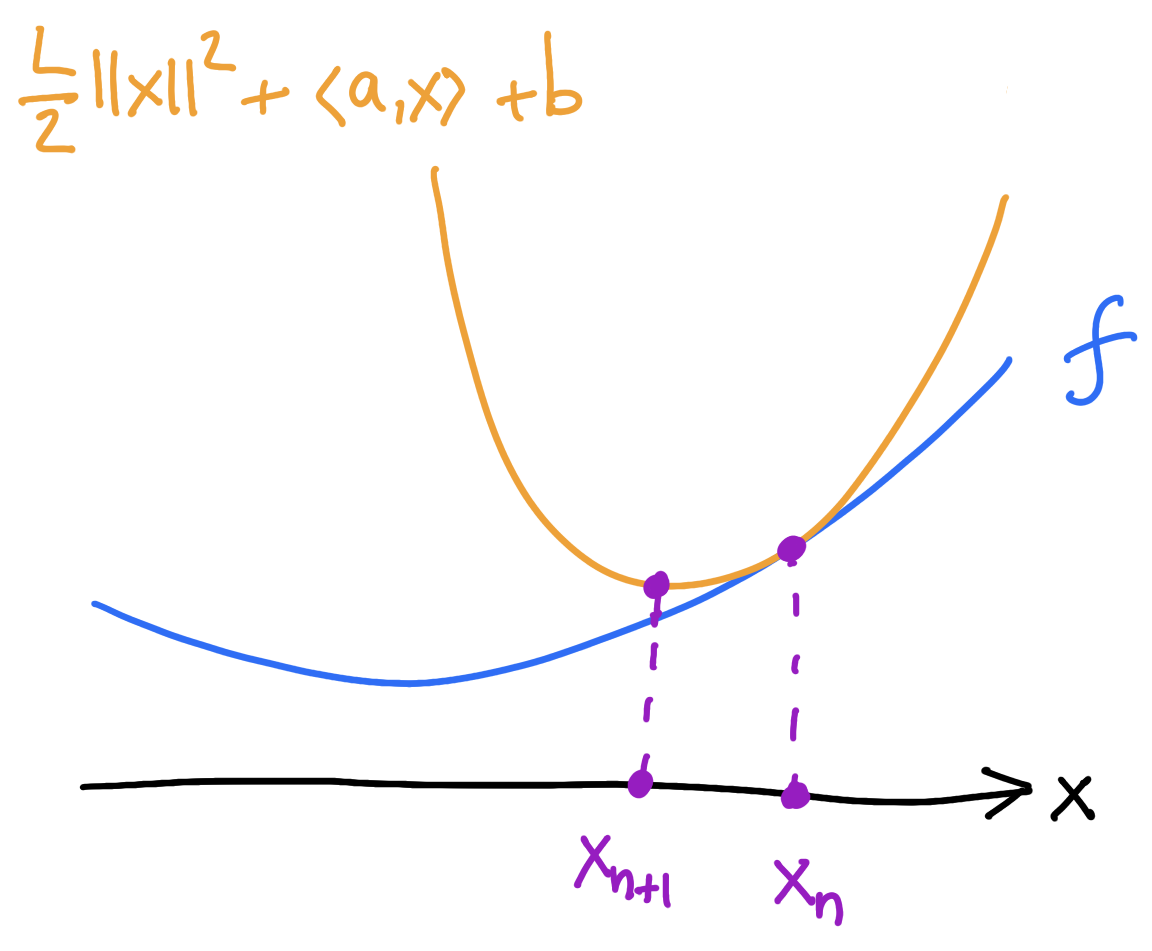
\[x_{n+1}=x_n-\frac{1}{L}\nabla f(x_n),\]
objective function \(f\colon \mathbb{R}^d\to\mathbb{R}\)
\(f\) is \(L\)-smooth if \[\nabla^2f\leq L I_{d\times d}\]
D E F I N I T I O N
\[f(x)\]
\[\leq\]
\[f(x_n)+\langle\nabla f(x_n),x-x_n\rangle+\frac{L}{2}\lVert x-x_n\rVert^2\]
Reformulating the majorize step
Majorize step ↔ \(y\)-update:
\[y_{n+1} = \argmin_{y}\phi(x_n,y)\]
Minimize step ↔ \(x\)-update:
\[x_{n+1} = \argmin_{x}\phi(x,y_{n+1})\]
Family of majorizing functions \(\phi(x,y)\)
\(\phi(\cdot,y_{n+1})\)
General cost
Given: \(X\) and \(f\colon X\to\mathbb{R}\)
Choose: \(Y\) and \(c(x,y)\)
\[f(x)\leq \underbrace{c(x,y)+f^c(y)}_{\phi(x,y)}\]
\(f\) is \(c\)-concave if
\[f(x)=\inf_{y\in Y}c(x,y)+f^c(y)\]
D E F I N I T I O N
\[f^c(y)=\sup_{x\in X}f(x)-c(x,y)\]
D E F I N I T I O N
\(c\)-transform
\(c(\cdot,y)+f^c(y)\)
(Moreau '66)
\(c(\cdot,y)+\lambda\)
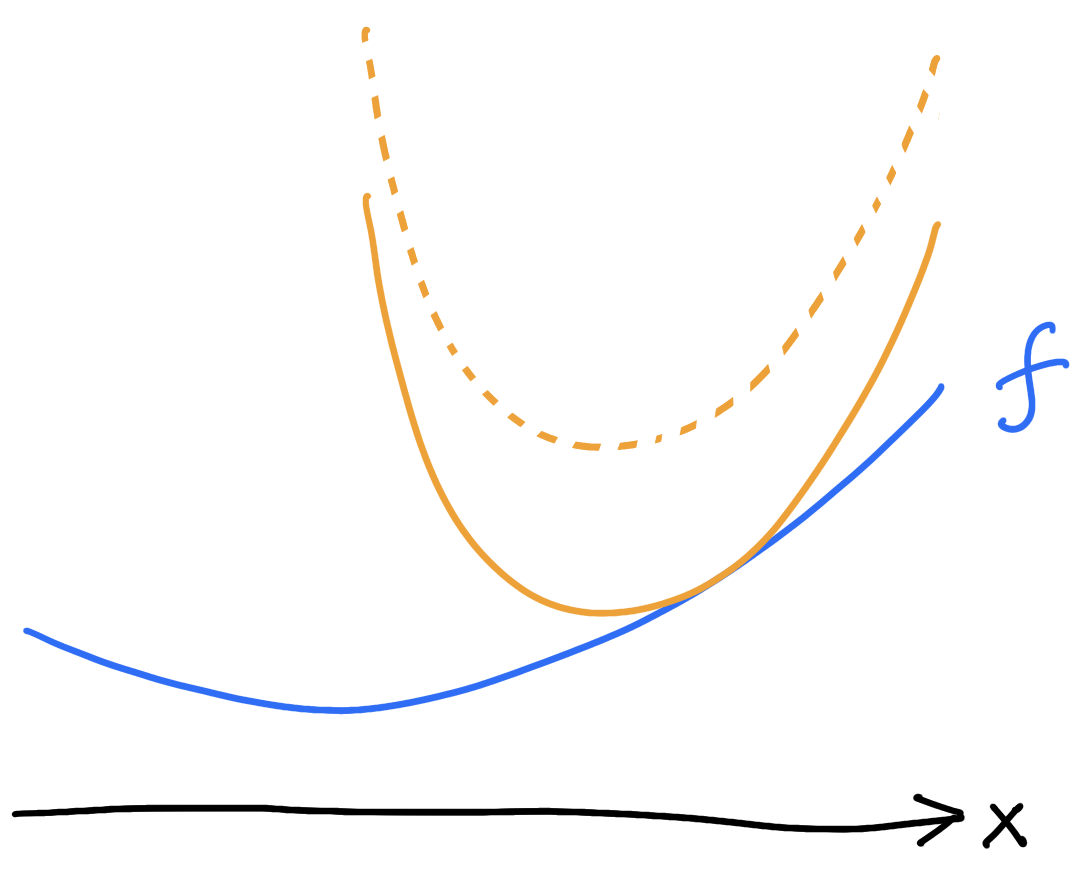
\(c\)-concavity is smoothness
\(f\) is \(c\)-concave if
\[f(x)=\inf_{y\in Y}c(x,y)+f^c(y)\]
D E F I N I T I O N
\(f\) is \(c\)-concave
\(f\) is not \(c\)-concave
\(c(x,y)=\frac{L}{2}\lVert x-y\rVert^2\)
\(f\) is \(c\)-concave \(\iff \nabla^2 f\leq L I_{d\times d}\)
Example
\[\inf_{x}f(x)=\inf_{x,y}c(x,y)+f^c(y)\]
Gradient descent with a general cost
(FL–PCAF '23)
\begin{aligned}
y_{n+1} &= \argmin_{y\in Y} c(x_n,y)+f^c(y)\\
x_{n+1} &= \argmin_{x\in X} c(x,y_{n+1})+f^c(y_{n+1})
\end{aligned}
\begin{aligned}
-\nabla_xc(x_n,y_{n+1})&=-\nabla f(x_n)\\
\nabla_xc(x_{n+1},y_{n+1})&=0
\end{aligned}
“majorize”
“minimize”
A L G O R I T H M
\(\phi(\cdot,y_{n+1})\)
\(\phi(x,y)=c(x,y)+f^c(y)\)
\(-\nabla_xc(x_n,y_{n+1})=-\nabla f(x_n)\)
\(y_{n+1}=\operatorname{c-exp}_{x_n}(-\nabla f(x_n))\)
\(\iff\)
Some examples
\(\,\,\,c(x,y)=\underbrace{u(x)-u(y)-\langle\nabla u(y),x-y\rangle}_{\qquad\quad\eqqcolon \,u(x|y)} \longrightarrow\) mirror descent
\(\,\,\,c(x,y)=u(y|x) \longrightarrow\) natural gradient descent
\(\,\,\,c(x,y)=\frac{L}{2}d_M^2(x,y)\longrightarrow\) Riemannian gradient descent
Newton
\[\nabla u(x_{n+1})-\nabla u(x_n)=-\nabla f(x_n)\]
\[x_{n+1}-x_n=-\nabla^2 u(x_n)^{-1}\nabla f(x_n)\]
\[x_{n+1}=\exp_{x_n}(-\frac{1}{L}\nabla f(x_n))\]
1. A new family of algorithms
2. Convergence theory
3. Applications
Gradient descent as alternating minimization
General method unifies gradient/mirror/natural gradient/Riemannian descent
Generalized smoothness and convexity
Optimal transport theory → local characterizations
Global rates for Newton
Explicit vs. implicit Riemannian gradient descent
2. Cross-convexity
\(f\) is \(\lambda\)-strongly \(c\)-cross-convex if for all \(x,x_n,\)
\[f(x) \geq f(x_n) + \delta_c(x,y_n;x_n,y_{n+1})+\lambda(c(x,y_n)-c(x_n,y_n)).\]
D E F I N I T I O N
\begin{aligned}
-\nabla_xc(x_n,y_{n+1})&=-\nabla f(x_n)\\
\nabla_xc(x_{n},y_{n})&=0
\end{aligned}
\(\delta_c(x',y';x,y)=[c(x,y')+c(x',y)]-[c(x,y)+c(x',y')]\)
Cross-difference:
Example: \(c(x,y)=\frac{L}{2}\lVert x-y\rVert^2\)
\[f(x)\geq f(x_n)+\langle\nabla f(x_n),x-x_n\rangle +\frac{\lambda L}{2}\lVert x-x_n\rVert^2\]
Convergence rates
If \(f\) is \(c\)-concave and \(c\)-cross-convex then
\[f(x_n)\le f(x) + \frac{c(x,y_0)-c(x_0,y_0)}{n}.\]
If \(f\) is \(\lambda\)-strongly \(c\)-cross-convex with \(0<\lambda<1\), then
\[f(x_n)\le f(x) + \frac{\lambda \,(c(x,y_0)-c(x_0,y_0))}{\Lambda^n-1},\]
where \(\Lambda\coloneqq(1-\lambda)^{-1}>1\).
T H E O R E M (FL–PCAF '23)
\[\left.\begin{aligned}f(x_{n+1})\leq c(x_{n+1},y_{n+1})+f^c(y_{n+1})\\~\end{aligned}\right\}\]
\(\implies f(x_{n+1})\leq f(x_{n})- [c(x_{n},y_{n+1})-c(x_{n+1},y_{n+1})]\)
\(f(x_{n+1}) \leq f(x)+ [c(x,y_n)-c(x_n,y_n)]\)
Proof.
\(f(x_{n})= c(x_{n},y_{n+1})+f^c(y_{n+1})\)
\(f(x_{n}) \leq f(x)+ c(x,y_n)-c(x,y_{n+1})\)
\(\implies\)
\(+c(x_n,y_{n+1})-c(x_{n},y_{n})\)
\(- [c(x,y_{n+1})-c(x_{n+1},y_{n+1})]\)
(“Fenchel–Young inequality”)
(\(c\)-concavity)
(cross-convexity)
The Kim–McCann geometry
\(\delta_c(x+\xi,y+\eta;x,y)=\underbrace{-\nabla^2_{xy}c(x,y)(\xi,\eta)}_{\text{Kim--McCann metric ('10)}}+o(\lvert\xi\rvert^2+\lvert\eta\rvert^2)\)
\(\delta_c(x',y';x,y)=\)
\[\inf_{\pi\in\Pi(\mu,\nu)}\iint_{X\times Y}c(x,y)\,\pi(dx,dy)\]
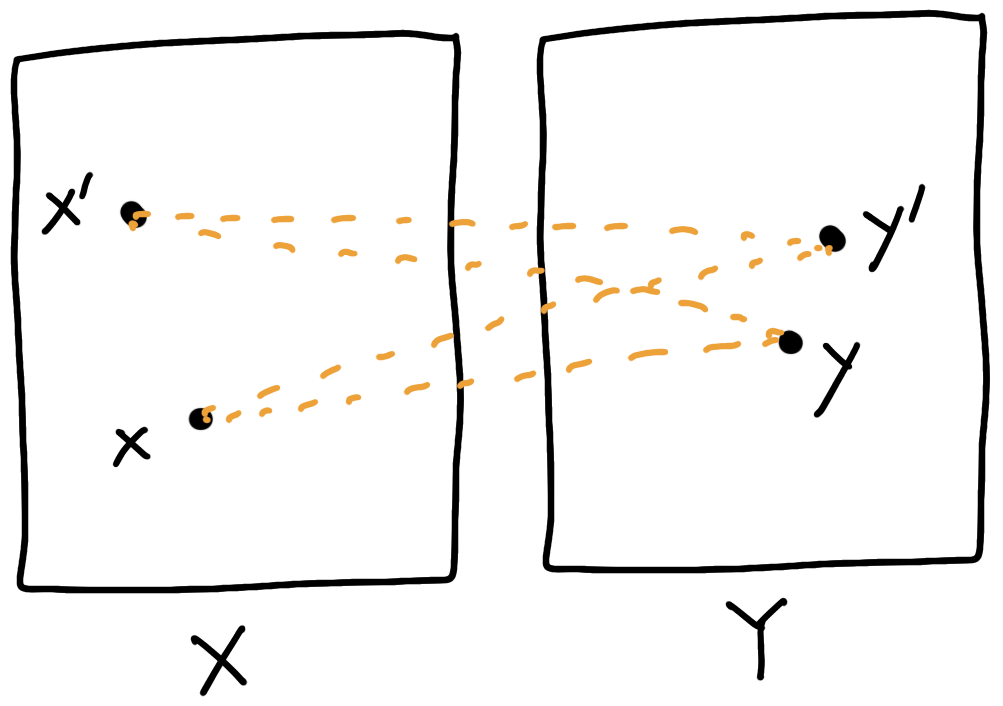
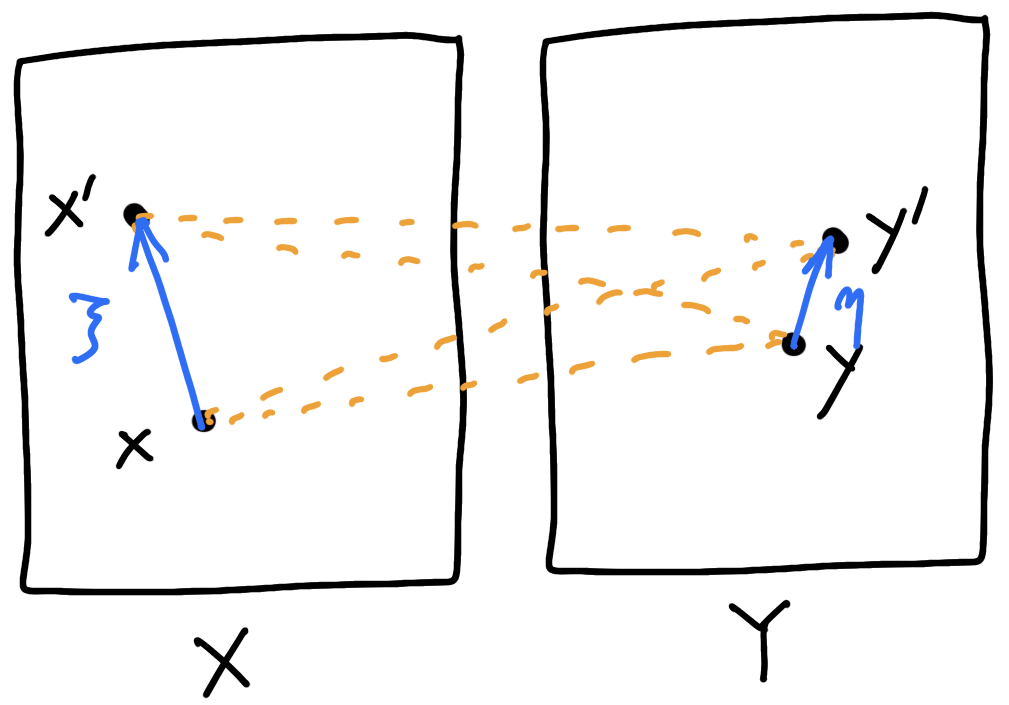
\([c(x,y')+c(x',y)]-[c(x,y)+c(x',y')]\)
➡ Kim–McCann geodesics
➡ Kim–McCann curvature: cross-curvature
Cross-curvature
The cross-curvature or Ma–Trudinger–Wang tensor is
\[\mathfrak{S}_c(\xi,\eta)=(c_{ik\bar s} c^{\bar s t} c_{t \bar\jmath\bar\ell}-c_{i\bar \jmath k\bar\ell}) \xi^i\eta^{\bar\jmath}\xi^k\eta^{\bar\ell}\]
(Ma–Trudinger–Wang ’05)
\[c_{i\bar \jmath}=\frac{\partial^2c}{\partial x^i\partial y^{\bar\jmath}},\dots\]
D E F I N I T I O N
T H E O R E M (Kim–McCann '11)
\[\mathfrak{S}_c\geq 0 \iff c(x(t),y)-c(x(t),y')\text{ convex in } t\]
for any Kim–McCann geodesic \(t\mapsto (x(t),y)\)
A local criteria for cross-convexity
Suppose that for all \(\bar x\in X\), there exists \(\hat y\in Y\) satisfying \(-\nabla_xc(\bar x,\hat y)=-\nabla f(\bar x)\) and such that
\[\nabla^2f(\bar x) \leq \nabla^2_{xx}c(\bar x,\hat y).\]
Then \(f\) is \(c\)-concave.
T H E O R E M (Trudinger–Wang '06)
Suppose that \(c\) has nonnegative cross-curvature.
Let \(\lambda>0\). Suppose that \[t\mapsto f(x(t))-\lambda c(x(t),\bar y)\] is convex on every Kim–McCann geodesic \(t\mapsto (x(t),\bar y)\) satisfying \(\nabla_xc(x(0),\bar y)=0\). Then \(f\) is \(\lambda\)-strongly \(c\)-cross-convex.
T H E O R E M (FL–PCAF '23)
1. A new family of algorithms
2. Convergence theory
3. Applications
Gradient descent as alternating minimization
General method unifies gradient/mirror/natural gradient/Riemannian descent
Generalized smoothness and convexity
Optimal transport theory → local characterizations
Global rates for Newton
Explicit vs. implicit Riemannian gradient descent
Global rates for Newton's method
\(c(x,y)=u(y|x)\longrightarrow\) Natural gradient descent:
\[x_{n+1}-x_n=-\nabla^2u(x_n)^{-1}\nabla f(x_n)\]
Newton's method: new global convergence rate.
New condition on \(f\) similar but different from self-concordance
T H E O R E M (FL–PCAF '23)
If \[\nabla^3u(\nabla^2u^{-1}\nabla f,-,-)\leq \nabla^2f\leq \nabla^2u+\nabla^3u(\nabla^2u^{-1}\nabla f,-,-)\] then
\[f(x_n)\leq f(x)+\frac{u(x_0|x)}{n}\]
Explicit vs. implicit Riemannian
\(c(x,y)=\frac{1}{2\tau} d_M^2(x,y)\)
2. Implicit: \(x_{n+1}=\argmin_{x} f(x)+\frac{1}{2\tau}d^2(x,x_n)\)
\(R\leq 0\): \(\nabla^2f\geq 0\) gives \(O(1/n)\) convergence rates
Wasserstein gradient flows, generalized geodesics (Ambrosio–Gigli–Savaré '05)
da Cruz Neto, de Lima, Oliveira ’98
Bento, Ferreira, Melo ’17
1. Explicit: \(x_{n+1}=\exp_{x_n}\big(-\tau\nabla f(x_n)\big)\)
\(R\geq 0\): (smoothness and) \(\nabla^2f\geq 0\) gives \(O(1/n)\) convergence rates
\(R\leq 0\): ? (nonlocal condition)
\[\operatorname*{minimize}_{x\in M} f(x)\]
\(R\geq 0\): if \(\mathfrak{S}_c\geq 0\) then convexity of \(f\) on Kim–McCann geodesics gives \(O(1/n)\) convergence rates
Thank you!
(SPO 2023-12-04) Gradient descent with a general cost
By Flavien Léger
