a tale of three categories
Fosco Loregian
-
Ph.D. at SISSA - Trieste (IT)
Stable homotopy theory, ∞-categories, derived AG -
University of Western Ontario (CA)
∞-categories, derivators - Masaryk University (CZ)
Accessible categories, derivators, 2-categories - Max Planck Inst. für Math. (DE)
2-categories, derivators, applied category theory - CMUC (PT)
who knows? Wait and see...
me, in a nutshell
stable ∞-categories
A n-simplex is a polytope with n vertices and a single arrow forall i ≤ j
\Delta^2
\Delta^3
\Delta^4
\dots
There is a category Δ modeling simplices:
finite nonempty totally ordered sets + monotone maps
face
degen
Every category is a suitable presheaf on Δ ([Δ°, Set] = simplicial sets):
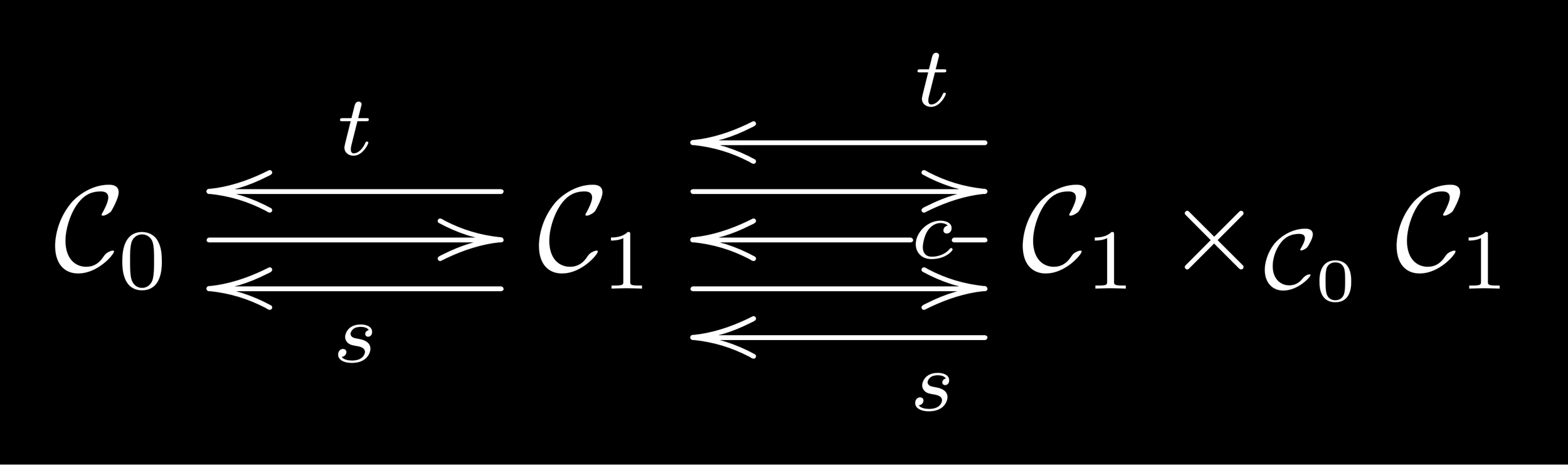
More formally, there is a functor i : Δ → Cat
- i is dense, thus
- the left ext. of Yoneda along i is a fully faithful embedding
N : {\bf Cat} \to [\boldsymbol{\Delta}^\text{op}, {\bf Set}]
sending a category to its nerve.
General result: Cat is an orthogonal class in simplicial sets
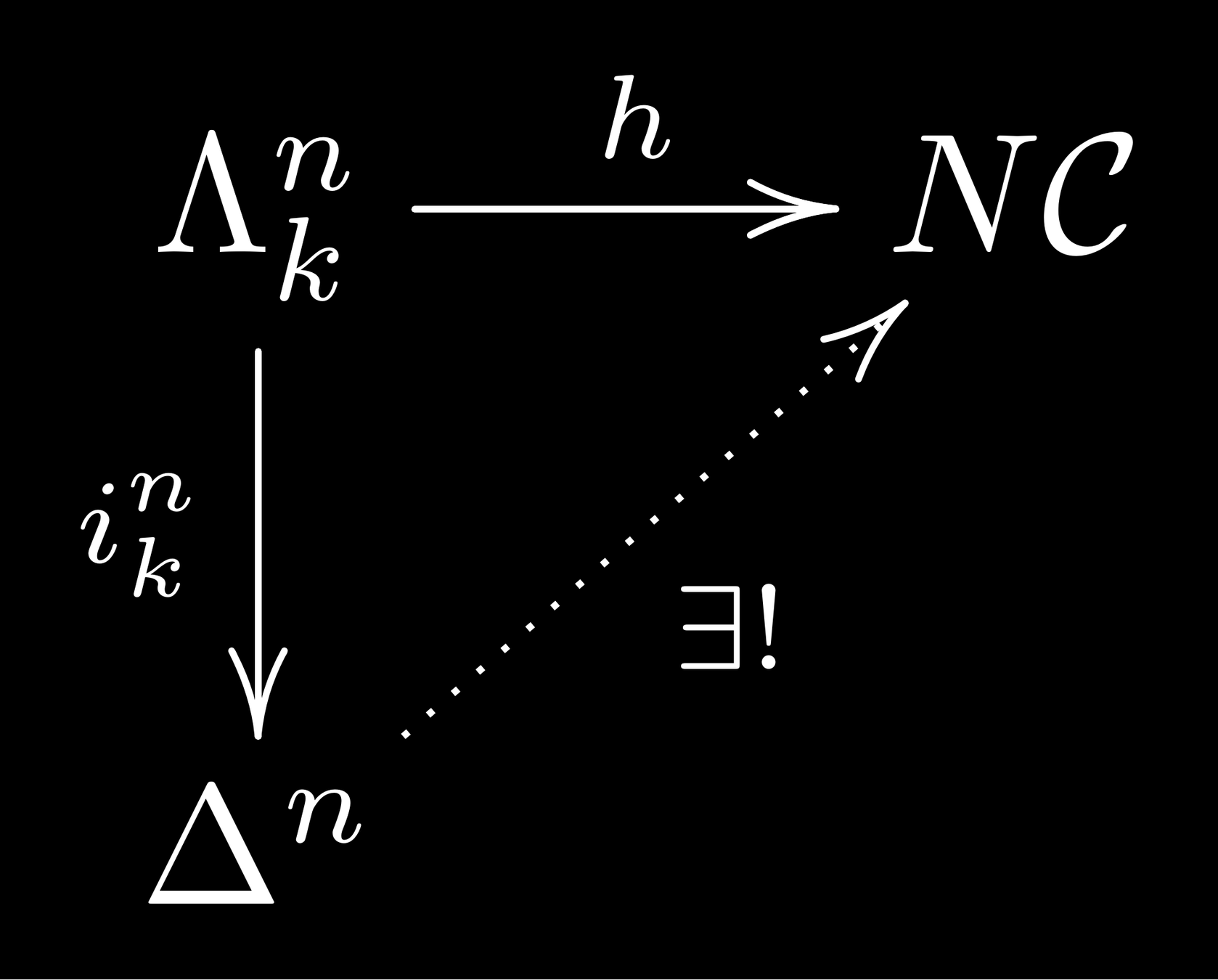
Every n-tuple of arrows eager to be composed has indeed a unique composite.
An ∞-category : an object injective wrt the same class of maps
Every n-tuple of arrows eager to be composed has a composite, unique up to a contractible space of choices.
Boom! you can redo category theory from scratch
- limits, colimits
- the Grothendieck construction
- Kan extensions
- adjunctions and monads
- accessible categories
- topos theory
- you-name-it
Turns out some parts of Mathematics are easier if stated in these terms:
- homological algebra : the scary part of algebraic topology
- higher algebra : the commutative algebra of ∞-categories
- 1-topos theory : a synthetic type theory,
- ∞-topos theory: a synthetic homotopy theory of homotopy types
- Applications in, like, everywhere.
Some conjectures proved with ∞-categories
- 2009 - [L] Proof of Baez-Dolan conjecture
Every FQFT (= a monoidal functor from an (∞,n)-category of cobordisms) is determined by its value on the point - 2014 - [LG] Proof of Weil's conjecture on Tamagawa numbers
Some weird formula full of ζ(n/2) is the measure of a geometric object - ??? - [HoTT] Foundation for Martin-Löf intuitionistic type teory with univalence
I heard you like type theories; what if they allowed you to do algebraic topology?
Wanna know more? Check kerodon.net!
stable ∞-categories
A stable ∞-category is an ∞-category
- with all finite limits and colimits
- such that a square is cartesian iff cocartesian
The homotopy category of a stable ∞-cat is always triangulated
The correspondence sending an abelian A into its derived category has a nice and clear universal property
Stable, rational, p-adic, ... homotopy theory are pieces of commutative algebra of ∞-categories
A t-structure on D triangulated is a pair of triangulated subcategories of D such that every object X lies in a sequence
X_{\le} \to X \to X_{\ge} \to \Sigma X_{\le}
("the part w/ negative homotopy groups", "the part w/ positive homotopy groups")
[FL14] : On stable ∞-cats a t-structure is a factorization system (E,M)
- such that E and M are 3-for-2 classes
- thus the category of E-cofibrant objects is coreflective
- and the category of M-fibrant objects is reflective
- cof/fib replacement are neg/pos truncation
(Algebraic) geometry has been reduced to (categorical) algebra (once again). Yay!
plan: redo theory of t-structures
- [FL15] On the set of t-structures there is a natural choice of Z-action (Z = the integers); study Z-equivariant monotone maps from a poset J to TS(C).
Bridgeland stability manifolds, Postnikov towers on ∞-toposes - [FL15b] Every stratified manifold (X,s) generates a pair of t-structure that can be glued together
recollements, stratified schemes, representation of algebras - Project: algebraic geometry is easier, with factorization systems.
Rational and p-adic homotopy ~ rational and p-adic geometry ~ number-theoretic factorization systems
Check. Done in my Ph.D.
Conjecture 1
is an interesting set [FL-PhD]*
every prime p defines
Blakers-Massey in char p is a thm about factorization systems
Real numbers? Eeew. go p-adic!
has an interest in chromatic homotopy
*Still unpublished!
\tiny \{ J \colon \mathbb R \to TS(\mathcal C) \mid J \text{ is Sorgenfrey continuous} \}
\tiny \{ J \colon \text{Spec}(\mathbb Z) \to TS(\mathcal C) \mid J \text{ is Zariski continuous} \}
conjecture 2
Fact: Bord(n) is the free (∞,n)-symmoncat on the point
monoidal functors Z : Bord(n) → Vect are completely classified and used in QFT
Morse theory is the theory of suitable factorization systems on Bord(n)
{critical points of a Morse function}
{critical values of a certain "slicing" J : R → FS(Bord(n))}
derivators
Too much ∞-categories make us dull boys.
Let's stop to dimension two.
A derivator is a strict 2-functor
\mathbb{D} : {\bf Cat}^\text{op} \to {\bf CAT}
satisfying sheafy conditions. They form the 2-category Der.
They subsume most of ∞-category theory (in a suitable sense, they are more general)
[LV17] : A t-structure on a stable derivator is still a certain kind of factorization system*
*And FS are still algebras for the "squaring" 2-monad ( _ )² : A ↦ A² (see [KT93])
[Lor18] : reflective subderivators correspond to reflective factorization systems, and to algebras for idempotent monads*
*(the "formal theory of monads" still holds in Der, a monad T : D → D is just defined objectwise)
To what extent category theory exports to the 2-category Der?
Well...
Uncle Ross to the rescue!
So: we have adjunctions, monads, factorization systems...
-
Formal category theory attempts to outline axioms on a 2-category K such that you can "do category theory" in K
- A Yoneda structure gives enough structure to K in order to state the Yoneda lemma; provides K with a calculus of Kan extensions
- A proarrow equipment gives K enough structure to concoct a calculus of profunctors; it is engineered to build a calculus of weighted co/limits
[DLL19]: Suitable assumptions on K and on the presheaf construction P( _ ) entail that these two frameworks are equivalent.
conjecture 3
There is a Yoneda structure on the 2-category of derivators
If this is true
- comprehensive account of various notions of accessible and locally presentable derivator using [DLL18]; categorical logic for derivators; derivator toposes?
- a convincing form of adjoint functor theorem for derivators: useful, innit?
- profunctors between derivators; fibered derivators; operads in derivator theory; applications in representation theory, stable homotopy, ...
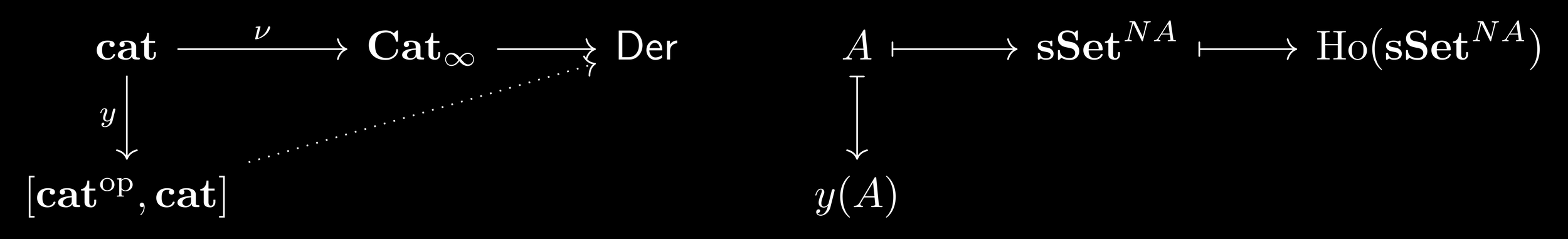
- cat = small categories;
- y is the Yoneda embedding;
- Ho(sPSh(A)) is always a derivator
Preparatory conjecture: there is a pseudo-YS on Der (all universal properties are pseudo-ified)
Fernando, are you here?
Applied category theory
Problem: It's all fun(ctors) and games until your grant finishes...
Solution: do applied mathematics. Make good money.
Save the world from climate change.
Avoid (or catalyze) next financial crisis.
functional programming
put the mo-ney in mo-nads
I've always wondered, how would a machine do mathematics?
For category theory, I think the answer is in a functional language with dependent types.
- Types form a (2?-)category Type of algebraic types
- I/O is modeled by a bunch of monads on Type
- parsing is made with monads on (readable) objects of Type
class Profunctor p where
dimap :: (a -> b) -> (c -> d) -> p b c -> p a d
dimap f g = lmap f . rmap g
* :: Profunctor b c -> Profunctor a b -> Profunctor a c
(p * q) = \x z -> exist y . ( p x y , q y z )Open Haskell's Data.Profunctor library
Welp, that's exactly profunctor composition!
\footnotesize \displaystyle P \star Q(X,Z) = \int^Y P(X,Y) \times Q(Y,Z)
A suitable kind of lens (a datatype to access nested records in a datatype) is described as a Tambara module
(profunctors on a monoidal domain A, compatible with an action of A on Prof(A,A))
Changing the action you obtain a whole lot of different lenses, to the point that there is a conjectural bijection between the two classes
Cool.
But we want more: generalize to other kinds of profunctors
A Petri net is a certain kind of multidigraph.
- Let Rep(P) be the category of graph morphisms P → Set
- it has a certain interest when P is regarded as a model of computation: F : P → Set describes "P-shaped" algorithms
- Change Set with Cat, get a fibration over P; give internal semantics to P-shaped algorithms
- Go one step further: consider displayed categories
Conjecture: they are a model for concurrent computation - Go one step further: what if in one of the nodes of a Petri net there's a nested Petri net?
these gadgets can be grafted like operads! Conjecture: they model recursive/sequential computation
\footnotesize F : P \to {\bf Prof}
In conclusion
A few things done better with category theory
-
Algebraic geometry and homotopy theory
yeah, we know the drill
-
Logic, constructive mathematics
uh uh, go on...
- Quantum mechanics [ZX, ACR], especially string theory [DCCT]
- The study of natural language processes [Lam, Jag, Coe,...]
- Designing a programming language [Bra]
- Proof-check the security of a web UI [Sta]
- Dynamical systems [Sp, Gog]
-
Computability theory [CH, CHH]
aha, now we're talking!
Thanks for your attention!
A tale of three categories
By Fouche Ehcuof
