Count triangles
Codeforces Round #643 (div. 2)
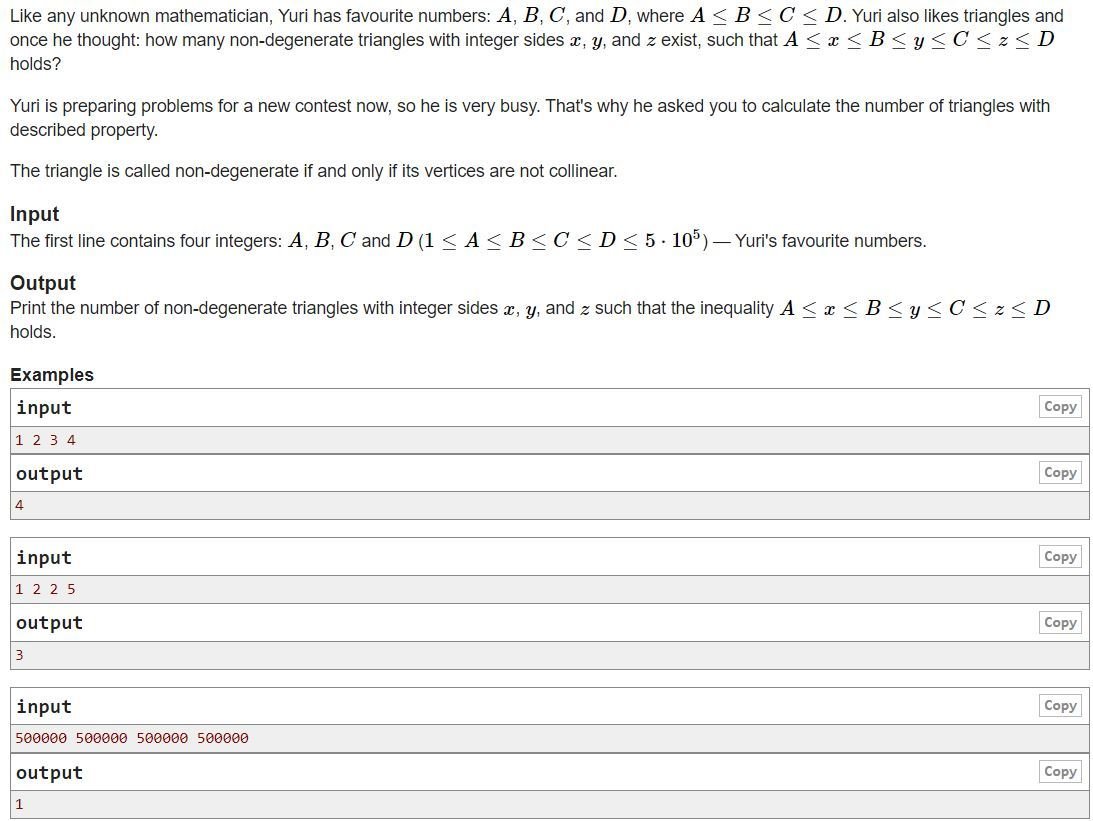
So, first of All, let's talk about non-degenerate triangles
What are they?
When three sides(x,y,z) of a triangle satisfy this inequality
that
x + y > z
y + z > x
x + z > y
We say it is a non-degenrate triangle.
Now In our case, We can choose x from A to B, y from B to C, and z from C to D inclusively.
Also,
1 <= A <= B <= C <= D
x
y
z
1 <= A <= x <= B <= y <= C <= z <= D
This equation simply implies that
x <= y <= z
We can see that we only need this inequality
x + y > z
We don't need other two inequalities to consider because they are automatically considered when we are choosing x, y, z.
since we have x <= y
and inequality y + z > x will always hold.
similarly for y <= z
and inequality x+z > y
Yeah! we get the Intuition to solve. Now let's solve it.
The Goal reduces to find all such triplets of x, y, z such that they satisfy this ineqaulity x + y > z
Now further problem reduces to finding all sums of x+y.
for (int x = A;x <= B;x++)
{
for (int y = B;y <= C;y++)
{
sums.push(x+y)
}
}TLE
Don't Panic
We can get these sums in linear complexity.
Prefix Sums
How to get Prefix sum to get these sums?
Let's See
Consider the case Where
A = 1, B = 3, C = 5, D = 10
1 <= x <= 3,
3 <= y <= 5
Fix x = 1 and vary y from 3 to 5
x = 1, y = 3
x+y =
4
Consider the case Where
A = 1, B = 3, C = 5, D = 10
1 <= x <= 3,
3 <= y <= 5
Fix x = 1 and vary y from 3 to 5
x = 1, y = 4
x+y =
4
5
Consider the case Where
A = 1, B = 3, C = 5, D = 10
1 <= x <= 3,
3 <= y <= 5
Fix x = 1 and vary y from 3 to 5
x = 1, y = 5
x+y =
4
5
6
Consider the case Where
A = 1, B = 3, C = 5, D = 10
1 <= x <= 3,
3 <= y <= 5
Fix x = 1 and vary y from 3 to 5
4
5
6
Here you can see that for a fix x and varying y sum is incrementing by 1 in every iteration.
x+B
x+C
Use Prefix Sum to get these sums.
How?
Take an array of count
index = sum
value = count of that sum
for(int x = 1;x <= B;x++)
{
count[x+B]++;
count[x+C+1]--;
}| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|---|
0
1
2
3
4
5
6
7
8
9
Use Prefix Sum to get these sums.
How?
Take an array of count
index = sum
value = count of that sum
for(int x = A;x <= B;x++)
{
count[x+B]++;
count[x+C+1]--;
}| 0 | 0 | 0 | 0 | 1 | 1 | 1 | -1 | -1 | -1 |
|---|
0
1
2
3
4
5
6
7
8
9
Use Prefix Sum to get these sums.
How?
Take an array of count
index = sum
value = count of that sum
for(int sum = 0;sum < count.size();sum++)
{
count[sum+1] += count[sum];
}| 0 | 0 | 0 | 0 | 1 | 2 | 3 | 2 | 1 | 0 |
|---|
0
1
2
3
4
5
6
7
8
9
Final count array
| 0 | 0 | 0 | 0 | 1 | 2 | 3 | 2 | 1 | 0 |
|---|
0
1
2
3
4
5
6
7
8
9
Now once you get the Count array you can easily check for every
count of that sum multiplied by the number of z (C <= z <= D) which satisfy that sum.
int triangles = 0;
for (int sum = 0;sum < count.size();sum++)
{
if (sum > C)
{
triangles += cnt[i]*(min(i-1, d) - c+1);
}
}| 0 | 0 | 0 | 0 | 1 | 2 | 3 | 2 | 1 | 0 |
|---|
0
1
2
3
4
5
6
7
8
9
int triangles = 0;
for (int sum = 0;sum < count.size();sum++)
{
if (sum > C)
{
triangles += cnt[sum]*(min(sum-1, D) - C+1);
}
}At sum = 4
No z since 4 < C(= 5)
| 0 | 0 | 0 | 0 | 1 | 2 | 3 | 2 | 1 | 0 |
|---|
0
1
2
3
4
5
6
7
8
9
int triangles = 0;
for (int sum = 0;sum < count.size();sum++)
{
if (sum > C)
{
triangles += cnt[sum]*(min(sum-1, D) - C+1);
}
}At sum = 5
No z since 5 = C(= 5)
| 0 | 0 | 0 | 0 | 1 | 2 | 3 | 2 | 1 | 0 |
|---|
0
1
2
3
4
5
6
7
8
9
int triangles = 0;
for (int sum = 0;sum < count.size();sum++)
{
if (sum > C)
{
triangles += cnt[sum]*(min(sum-1, D) - C+1);
}
}At sum = 6
since 6 > C(= 5)
triangles += 3*(1)
triangles = 3
| 0 | 0 | 0 | 0 | 1 | 2 | 3 | 2 | 1 | 0 |
|---|
0
1
2
3
4
5
6
7
8
9
int triangles = 0;
for (int sum = 0;sum < count.size();sum++)
{
if (sum > C)
{
triangles += cnt[sum]*(min(sum-1, D) - C+1);
}
}At sum = 7
since 7 > C(= 5)
triangles += 2*(2)
triangles =
7
| 0 | 0 | 0 | 0 | 1 | 2 | 3 | 2 | 1 | 0 |
|---|
0
1
2
3
4
5
6
7
8
9
At sum = 8
since 8 > C(= 5)
triangles += 1*(3)
triangles =
10
We got the number of Triangles in linear time
Codeforces div 2(643) problem C
By gauravsahu
