CONVEX
HULL
(Graham's Scan Algorithm)
Geometry In Competitive Programming
What is convex polygon?
A convex polygon is defined as a polygon with all its interior angles less than 180°.
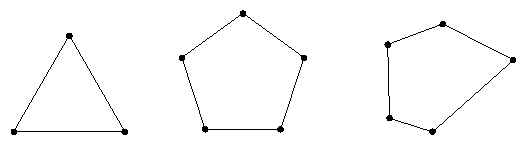
Convex Polygons
Concave Polygons
Examples
Now, What is a Convex Hull?
X
Y
Examples
Now, What is a Convex Hull?
X
Y
Convex Hull
The smallest convex polygon that contains all the given points.
Examples
What about Collinear points?
X
Y
The smallest convex polygon that contains all the given points.
Examples
What about Collinear points?
X
Y
The smallest convex polygon that contains all the given points.
Since we are talking smallest hence we will take only first and last point for collinear points.
Examples
What about Collinear points?
X
Y
The smallest convex polygon that contains all the given points.
Since we are talking smallest hence we will take only first and last point for collinear points.
Examples
About The Algorithm
Graham's Scan Algorithm
(1979)
Complexity O(NlogN)
where N is the number of points given
Examples
Orientation
P
Q
R
Orientation Between PQ and PR = Clockwise
Examples
Orientation
P
Q
R
Orientation Between PR and PQ = Counter Clockwise
Examples
Now How do we get orientation?
P
Q
R
Orientation Between PQ and PR
Examples
Now How do we get orientation?
P
Q
R
Orientation Between PQ and PR
Clockwise
Examples
Now How do we get orientation?
P
Q
R
Orientation Between PR and PQ
Counter Clockwise
Examples
Now How do we get orientation?
P
Q
R
Orientation Between PQ and QR
Examples
Now How do we get orientation?
P
Q
R
Orientation Between PQ and QR
m2
m1
Examples
Now How do we get orientation?
P
Q
R
Orientation Between PQ and QR
m2
m1
m1 > m2 => clockwise
Examples
Now How do we get orientation?
P
Q
R
Orientation Between PQ and QR
m2
m1
m1 > m2 => clockwise
Examples
Now How do we get orientation?
P
Q
R
Orientation Between PQ and QR
m2
m1
m1 > m2 => clockwise
Examples
Now How do we get orientation?
P
Q
R
Orientation Between PQ and QR
m2
m1
m1 > m2 => clockwise
Examples
Now How do we get orientation?
P
Q
R
Orientation Between PQ and QR
m2
m1
m2 > m1 => counter\ clockwise
Examples
Now How do we get orientation?
P
Q
R
Orientation Between PQ and QR
m2
m1
m2 > m1 => counter\ clockwise
Examples
Now How do we get orientation?
P
Q
R
Orientation Between PQ and QR
m2
m1
m2 > m1 => counter\ clockwise
Move on to the Algorithm
X
Y
N Points
Solution
To see the solution first of all think how numbers are added in binary
max(\sum_{i=1}^n (A_i\ \& X))
101(5)
001(1)
110(6)
111(7)
12+4
Solution
To see the solution first of all think how numbers are added in binary
max(\sum_{i=1}^n (A_i\ \& X))
101(5)
001(1)
110(6)
111(7)
12+4+3 = 19
Solution
101(5)
001(1)
110(6)
111(7)
12+4+3 = 19
From this example we have clearly understood that the sum depends on the product of number of 1's and positional value.
Solution
101(5)
001(1)
110(6)
111(7)
12+4+3 = 19
We have a X in which we can set 1's at exactly k times.
Solution
101(5)
001(1)
110(6)
111(7)
12+4+3 = 19
if at ith position of X if we set the ith bit in X that means we will have the value associated with that sum.
Solution
101(5)
001(1)
110(6)
111(7)
12+4+3 = 19
if at ith position of X if we set the ith bit in X that means we will have the value associated with that sum.
100
sum 12
Solution
101(5)
001(1)
110(6)
111(7)
12+4+3 = 19
if at ith position of X if we set the ith bit in X that means we will have the value associated with that sum.
010
sum 4
Solution
101(5)
001(1)
110(6)
111(7)
12+4+3 = 19
if at ith position of X if we set the ith bit in X that means we will have the value associated with that sum.
001
sum 3
Solution
101(5)
001(1)
110(6)
111(7)
12+4+3 = 19
if at ith position of X if we set the ith bit in X that means we will have the value associated with that sum.
001
sum 3
if the value of k = 1 where will you place that 1 among three positions obviously at first because it is producing more value to sum instead of others
100
sum 12
010
sum 4
Solution
101(5)
001(1)
110(6)
111(7)
12+4+3 = 19
if at ith position of X if we set the ith bit in X that means we will have the value associated with that sum.
001
sum 3
if the value of k = 2 where will you place that 2 1's among three positions at first and at second because it is producing more value to sum instead of others.
100
sum 12
010
sum 4
Solution
Thus we can produce a solution by selecting the k position which are adding k maximum values to the sum.
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pb push_back
#define all(c) (c).begin(),(c).end()
#define rall(c) (c).rbegin(),(c).rend()
bool cmp(pair<ll, ll>& p1, pair<ll, ll>& p2)
{
if (p1.first < p2.first)
{
return false;
}
else if (p1.first == p2.first)
{
if (p1.second > p2.second)
return false;
}
return true;
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
#endif
int t;
cin >> t;
while(t--)
{
int n,k;
cin >> n >> k;
std::vector<ll> v(n);
for (int i = 0; i < n; ++i)
{
cin >> v[i];
}
std::vector<pair<ll,ll>> b(31);
for (int i = 0; i <= 30; ++i)
{
ll cnt = 0;
for (int j = 0; j < n; ++j)
{
if (v[j] & (ll)pow((ll)2,(ll)i))
cnt++;
}
b[i].first = cnt*pow((ll)2, (ll)i);
b[i].second = i;
}
sort(all(b),cmp);
ll ans = 0;
for (int i = 0;i < k;i++)
{
ans += pow((ll)2,(ll)b[i].second);
}
cout << ans << "\n";
}
return 0;
}
Any Doubts
If you still have any doubts you can comment your doubts in the comment section.
If you have a better approach than this you can also comment it out.
Like, Share, Subscribe!
If you like our efforts Please Do Like this video, share it with your friends who was not able to solve this problem.
Also Do subscribe this channel because more video Editorials and coding related content is coming on this channel.
Like, Share, Subscribe!
Maximum AND
By gauravsahu
