Trie & Segment Tree

http://www.zhitongguigu.com/

Trie Tree (Prefix Tree)

http://www.zhitongguigu.com/

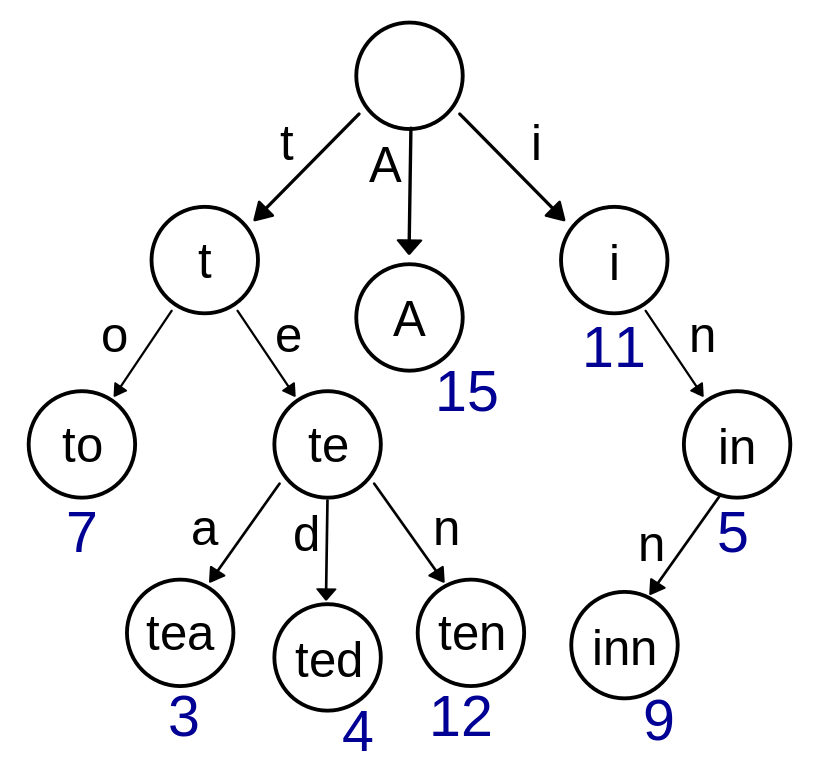
"A","to", "tea", "ted", "ten", "i", "in", "inn"

Trie Tree (Prefix Tree)

http://www.zhitongguigu.com/

Why Trie?

1. Prefix

(autocomplete, dictionary, phone book)

2. Order

3. Hash table?

O(1), but collision O(n)

Trie Tree (Prefix Tree)

http://www.zhitongguigu.com/

Interview

insert
search

Trie Tree (Prefix Tree)

http://www.zhitongguigu.com/

abat

absent

absolute

absolve

absorb

base

basic

link

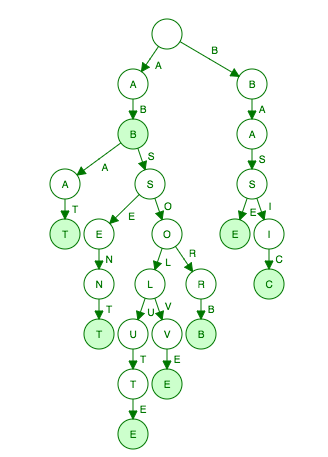
Trie Tree (Prefix Tree)

http://www.zhitongguigu.com/

public class Trie {

    /** Initialize your data structure here. */
    public Trie() {
        
    }
    
    /** Inserts a word into the trie. */
    public void insert(String word) {
        
    }
    
    /** Returns if the word is in the trie. */
    public boolean search(String word) {
        
    }
}

/**
 * Assume only lower case a - z.
 * Your Trie object will be instantiated and called as such:
 * Trie obj = new Trie();
 * obj.insert(word);
 * boolean param_2 = obj.search(word);
 */

Trie Tree (Prefix Tree)

http://www.zhitongguigu.com/

class TrieNode {
    TrieNode[] children;
    boolean isWord;
    public TrieNode() {
        this.children = new TrieNode[26];
        this.isWord = false;
    }
}

TreeNode

Trie Tree (Prefix Tree)

http://www.zhitongguigu.com/

public class Trie {
    private final char CHAR_A = 'a';
    private TrieNode root;

    public Trie() {
        root = new TrieNode();
    }

    // Inserts a word into the trie.
    public void insert(String word) {
        TrieNode p = root;
        for (char c : word.toCharArray()) {
            if (p.children[c - CHAR_A] == null) {
                p.children[c - CHAR_A] = new TrieNode();
            }
            p = p.children[c - CHAR_A];
        }
        p.isWord = true;
    }
}

Insert

Trie Tree (Prefix Tree)

http://www.zhitongguigu.com/

public class Trie {
    private final char CHAR_A = 'a';
    private TrieNode root;

    public Trie() {
        root = new TrieNode();
    }

    // Returns if the word is in the trie.
    public boolean search(String word) {
        TrieNode p = root;
        for (char c : word.toCharArray()) {
            if (p.children[c - CHAR_A] == null) {
                return false;
            }
            p = p.children[c - CHAR_A];
        }
        return p.isWord;
    }
}

Trie Tree (Prefix Tree)

http://www.zhitongguigu.com/

public class Trie {
    private final char CHAR_A = 'a';
    private TrieNode root;

    public Trie() {
        root = new TrieNode();
    }

    // Returns if there is any word in the trie
    // that starts with the given prefix.
    public boolean startsWith(String prefix) {
        TrieNode p = root;
        for (char c : prefix.toCharArray()) {
            if (p.children[c - CHAR_A] == null) {
                return false;
            }
            p = p.children[c - CHAR_A];
        }
        return true;
    }
}

Startwith

http://www.zhitongguigu.com/

public class Trie {
    private final char CHAR_A = 'a';
    private TrieNode root;

    public Trie() {
        root = new TrieNode();
    }

    // Inserts a word into the trie.
    public void insert(String word) {
        TrieNode p = root;
        for (char c : word.toCharArray()) {
            if (p.children[c - CHAR_A] == null) {
                p.children[c - CHAR_A] = new TrieNode();
            }
            p = p.children[c - CHAR_A];
        }
        p.isWord = true;
    }

    // Returns if the word is in the trie.
    public boolean search(String word) {
        TrieNode node = helper(word);
        return (node != null && node.isWord);
    }

    // Returns if there is any word in the trie
    // that starts with the given prefix.
    public boolean startsWith(String prefix) {
        return helper(prefix) != null;
    }
    
    private TrieNode helper(String s) {
        TrieNode p = root;
        for (char c : s.toCharArray()) {
            if (p.children[c - CHAR_A] == null) {
                return null;
            }
            p = p.children[c - CHAR_A];
        }
        return p;
    }
}

Trie Tree (Prefix Tree)

http://www.zhitongguigu.com/

search with regex

Example

addWord("bad")
addWord("dad")
addWord("mad")
search("pad") -> false
search("bad") -> true
search(".ad") -> true
search("b..") -> true

Trie Tree (Prefix Tree)

http://www.zhitongguigu.com/

public class Trie {
    private final char CHAR_A = 'a';
    private final char DOT = '.';
    private TrieNode root;

    public Trie() {
        root = new TrieNode();
    }

    // Returns if the word is in the data structure. A word could
    // contain the dot character '.' to represent any one letter.
    public boolean searchWithRegex(String word) {
        return helper(word, 0, root);
    }
    
    private boolean helper(String s, int index, TrieNode p) {
        if (index == s.length()) {
            return p.isWord;
        }
        char c = s.charAt(index);
        if (c == DOT) {
            for (int i = 0; i < p.children.length; i++) {
                if (p.children[i] != null && helper(s, index + 1, p.children[i])) {
                    return true;
                }
            }
            return false;
        } else {
            return (p.children[c - CHAR_A] != null && helper(s, index + 1, p.children[c - CHAR_A]));
        }
    }
}

search with regex

Word Square

Given a set of words (without duplicates), find all word squares you can build from them.

A sequence of words forms a valid word square if the kth row and column read the exact same string, where 0 ≤ k < max(numRows, numColumns).

For example, the word sequence ["ball","area","lead","lady"] forms a word square because each word reads the same both horizontally and vertically.

b a l l
a r e a
l e a d
l a d y

Note:

There are at least 1 and at most 1000 words.

All words will have the exact same length.

Word length is at least 1 and at most 5.

Each word contains only lowercase English alphabet a-z.

Word Square

Example 1:

Input:
["area","lead","wall","lady","ball"]

Output:
[
  [ "wall",
    "area",
    "lead",
    "lady"
  ],
  [ "ball",
    "area",
    "lead",
    "lady"
  ]
]

Example 2:

Input:
["abat","baba","atan","atal"]

Output:
[
  [ "baba",
    "abat",
    "baba",
    "atan"
  ],
  [ "baba",
    "abat",
    "baba",
    "atal"
  ]
]

Explanation:
The output consists of two word squares. The order of output does not matter 
(just the order of words in each word square matters).

http://www.zhitongguigu.com/

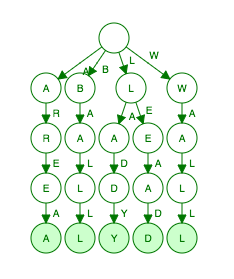
Word Square

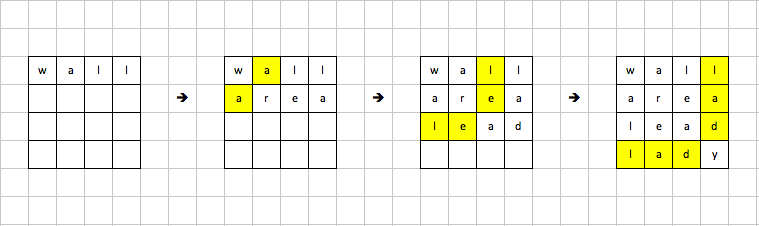
Example: ["wall","area","lead","lady","ball"]

What I care?

All the words with a given prefix

Word Square

Trie Tree

http://www.zhitongguigu.com/

public class Solution {
    private final char CHAR_A = 'a';
    public List<List<String>> wordSquares(String[] words) {
        List<List<String>> res = new ArrayList<>();
        if(words == null || words.length == 0) return res;
        Node root = buildTree(words);
        helper(new ArrayList<String>(), root, res, words[0].length());
        return res; 
    }

    private Node buildTree(String[] words) {
        Node root = new Node();
        for (String word : words) {
            Node p = root;
            p.list.add(word);
            for (char c : word.toCharArray()) {
                if (p.children[c - CHAR_A] == null) {
                    p.children[c - CHAR_A] = new Node();
                }
                p = p.children[c - CHAR_A];
                p.list.add(word);
            }
        }
        return root;
    }
    
    private void helper(List<String> cur, Node root, List<List<String>> res, int len){
        if (cur.size() == len){
            res.add(new ArrayList<String>(cur));
        } else {
            Node p = root; 
            for (int i = 0; i <= cur.size(); i++) {
                if(p == null || p.list.size() == 0) return;
                p = (i == cur.size()) ? p : p.children[cur.get(i).charAt(cur.size()) - CHAR_A];
            }
            for (String word : p.list){
                cur.add(word);
                helper(cur, root, res, len);
                cur.remove(cur.size()-1);
            }
        }
    }
    class Node{
        Node[] children = new Node[26];
        List<String> list = new ArrayList<>();
    }
}

Trie Tree Summary

http://www.zhitongguigu.com/

Trie BU

TopCoder

GeeksforGeeks

Prefix
Hash Table
Searching String

Segment Tree

http://www.zhitongguigu.com/

Sum of Given Range

http://www.zhitongguigu.com/

The Problem

We are given an array: arr[0 . . . n-1].
1 Find the sum of elements from index l to r where 0 <= l <= r <= n-1 (Query)

2 Change value of a specified element of the array to a new value x. We need to do arr[i] = x where 0 <= i <= n-1 (Update)

http://www.zhitongguigu.com/

Brute force

Sum: O(n)

Update: O(1)

Sum of Given Range

http://www.zhitongguigu.com/

create another array and store sum from start to i at the ith index in this array.

Sum: O(1)

Update: O(n)

Benefits if the number of query operations are large and very few updates.

Sum of Given Range

Is there a way to save the sum more efficiently?

🤔

http://www.zhitongguigu.com/

Segment Tree

Sum: O(log n)

Update: O(log n)

Optimal solution.

Sum of Given Range

Segment Tree

http://www.zhitongguigu.com/

We are given an array: arr[0 . . . n-1].
1 Find the sum of elements from index l to r where 0 <= l <= r <= n-1 (Query)

2 Change value of a specified element of the array to a new value x. We need to do arr[i] = x where 0 <= i <= n-1 (Update)

Given nums = [1, 3, 5]

sumRange(0, 2) -> 9
update(1, 2)
sumRange(0, 2) -> 8

What kind of tree this is?

🤔

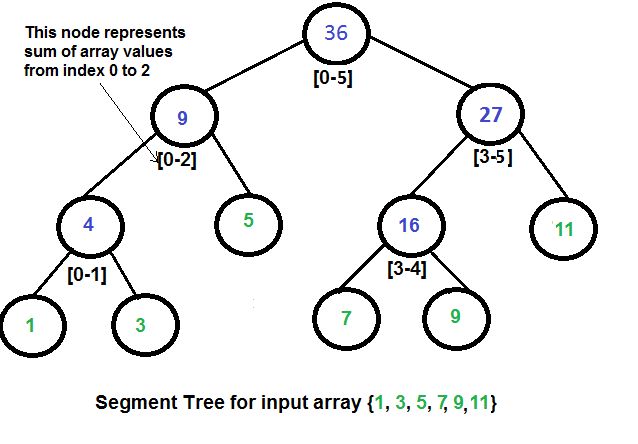
ex: [1,3,5,7,9,11]

Segment Tree

http://www.zhitongguigu.com/

Analyze

http://www.zhitongguigu.com/

public class NumArray {
    class Node {
        int start, end, val;
        Node left, right;
        public Node(int start, int end) {
            this.start = start;
            this.end = end;
        }
    }
    Node _root = null;
    public NumArray(int[] nums) {
        if (nums == null || nums.length == 0) {
            _root = new Node(0, 0);
        } else {
            _root = buildTree(nums, 0, nums.length - 1);
        }
    }
}

First of all

Class
Node
Constructor

http://www.zhitongguigu.com/

public class NumArray {
    private Node buildTree(int[] nums, int s, int e) {
        Node root = new Node(s, e);
        if (s == e) {
            root.val = nums[s];
            return root;
        }
        int mid = s + (e - s) / 2;
        root.left = buildTree(nums, s, mid);
        root.right = buildTree(nums, mid + 1, e);
        root.val = root.left.val + root.right.val;
        return root;
    }

    void update(int i, int val) {
        update(i, val, _root);
    }

    public int sumRange(int i, int j) {
        return query(i, j, _root);
    }
}

Then

Tree construction
Method interface

(Recursively)

http://www.zhitongguigu.com/

public class NumArray {
    private void update(int i, int val, Node node) {
        if (i < node.start || i > node.end) {
            return;
        }
        if (node.start == node.end && node.start == i) {
            node.val = val;
            return;
        }
        int mid = node.start + (node.end - node.start) / 2;
        if (i > mid) {
            update(i, val, node.right);
        } else {
            update(i, val, node.left);
        }
        node.val = node.left.val + node.right.val;
    }

    private int query(int i, int j, Node node) {
        if (i > node.end || j < node.start) {
            return 0;
        }
        if (i <= node.start && j >= node.end) {
            return node.val;
        }
        int mid = node.start + (node.end - node.start) / 2;
        int left = query(i, Math.min(mid, j), node.left);
        int right = query(Math.max(mid + 1, i), j, node.right);
        return left + right;
    }
}

update
query

http://www.zhitongguigu.com/

public class NumArray {
    class Node {
        int start, end, val;
        Node left, right;
        public Node(int start, int end) {
            this.start = start;
            this.end = end;
        }
    }
    Node _root = null;
    public NumArray(int[] nums) {
        if (nums == null || nums.length == 0) {
            _root = new Node(0, 0);
        } else {
            _root = buildTree(nums, 0, nums.length - 1);
        }
    }

    void update(int i, int val) {
        update(i, val, _root);
    }

    public int sumRange(int i, int j) {
        return query(i, j, _root);
    }

    private void update(int i, int val, Node node) {
        if (i < node.start || i > node.end) {
            return;
        }
        if (node.start == node.end && node.start == i) {
            node.val = val;
            return;
        }
        int mid = node.start + (node.end - node.start) / 2;  //make this a method?
        if (i > mid) {
            update(i, val, node.right);
        } else {
            update(i, val, node.left);
        }
        node.val = node.left.val + node.right.val;
    }

    private int query(int i, int j, Node node) {
        if (i > node.end || j < node.start) {
            return 0;
        }
        if (i <= node.start && j >= node.end) {
            return node.val;
        }
        int mid = node.start + (node.end - node.start) / 2;  //make this a method?
        int left = query(i, Math.min(mid, j), node.left);
        int right = query(Math.max(mid + 1, i), j, node.right);
        return left + right;
    }

    private Node buildTree(int[] nums, int s, int e) {
        Node root = new Node(s, e);
        if (s == e) {
            root.val = nums[s];
            return root;
        }
        int mid = s + (e - s) / 2;  //make this a method?
        root.left = buildTree(nums, s, mid);
        root.right = buildTree(nums, mid + 1, e);
        root.val = root.left.val + root.right.val;
        return root;
    }
}

Min of Given Range

http://www.zhitongguigu.com/

We are given an array: arr[0 . . . n-1].
1 Find the min of elements from index l to r where 0 <= l <= r <= n-1 (Query)

2 Change value of a specified element of the array to a new value x. We need to do arr[i] = x where 0 <= i <= n-1 (Update)

Count of Smaller Numbers After Self

http://www.zhitongguigu.com/

You are given an integer array nums and you have to return a new counts array. The counts array has the property where counts[i] is the number of smaller elements to the right of nums[i].

Segment Tree? Really?

🤔

Example:

Given nums = [5, 2, 6, 1]

To the right of 5 there are 2 smaller elements (2 and 1).
To the right of 2 there is only 1 smaller element (1).
To the right of 6 there is 1 smaller element (1).
To the right of 1 there is 0 smaller element.
Return the array [2, 1, 1, 0].

Count of Smaller Numbers After Self

http://www.zhitongguigu.com/

What should the node be?

What's the query?

What's the update?

Example:

Given nums = [5, 2, 6, 1]

To the right of 5 there are 2 smaller elements (2 and 1).
To the right of 2 there is only 1 smaller element (1).
To the right of 6 there is 1 smaller element (1).
To the right of 1 there is 0 smaller element.
Return the array [2, 1, 1, 0].

http://www.zhitongguigu.com/

Node
countSmaller
buildTree

public class Solution {
    class Node {
        int start, end, count;
        Node left, right;
        public Node(int start, int end) {
            this.start = start;
            this.end = end;
        }
    }
    public List<Integer> countSmaller(int[] nums) {
        int arrMin = Integer.MAX_VALUE;
        int arrMax = Integer.MIN_VALUE;
        for (int i : nums) {
            arrMin = Math.min(i, arrMin);
            arrMax = Math.max(i, arrMax);
        }
        Node root = buildTree(arrMin, arrMax);
        Integer[] res = new Integer[nums.length];
        for (int i = nums.length - 1; i >=0; i--) {
            res[i] = query(root, arrMin, nums[i] - 1);
            update(root, nums[i]);
        }
        return new ArrayList<Integer>(Arrays.asList(res));
    }
    private Node buildTree(int start, int end) {
        if (start == end) {
            return new Node(start, end);
        }
        int mid = start + (end - start) / 2;
        Node root = new Node(start, end);
        root.left = buildTree(start, mid);
        root.right = buildTree(mid + 1, end);
        return root;
    }
}

http://www.zhitongguigu.com/

query
update

public class Solution {
    private int query(Node node, int start, int end) {
        if (start > node.end || end < node.start) {
            return 0;
        }
        if (start <= node.start && end >= node.end) {   // start?
            return node.count;
        }
        int mid = node.start + (node.end - node.start) / 2;
        int left = query(node.left, start, Math.min(mid, end));
        int right = query(node.right, Math.max(mid, start), end);
        return left + right;
    }
    private int update(Node node, int val) {
        if (node.start == node.end && node.start == val) {
            node.count += 1;
            return node.count;
        }
        if (val < node.start || val > node.end) {
            return node.count;
        }
        int left = update(node.left, val);
        int right = update(node.right, val);
        node.count = left + right;
        return node.count;
    }
}

    private int query(Node node, int end) {
        if (end < node.start) {
            return 0;
        }
        if (end >= node.end) {
            return node.count;
        }
        int mid = node.start + (node.end - node.start) / 2;
        int left = query(node.left, Math.min(mid, end));
        int right = query(node.right, end);
        return left + right;
    }
}

http://www.zhitongguigu.com/

public class Solution {
    class Node {
        int start, end, count;
        Node left, right;
        public Node(int start, int end) {
            this.start = start;
            this.end = end;
        }
    }
    public List<Integer> countSmaller(int[] nums) {
        int arrMin = Integer.MAX_VALUE;
        int arrMax = Integer.MIN_VALUE;
        for (int i : nums) {
            arrMin = Math.min(i, arrMin);
            arrMax = Math.max(i, arrMax);
        }
        Node root = buildTree(arrMin, arrMax);
        Integer[] res = new Integer[nums.length];
        for (int i = nums.length - 1; i >=0; i--) {
            res[i] = query(root, nums[i] - 1);
            update(root, nums[i]);
        }
        return new ArrayList<Integer>(Arrays.asList(res));
    }
    private Node buildTree(int start, int end) {
        if (start == end) {
            return new Node(start, end);
        }
        int mid = start + (end - start) / 2;
        Node root = new Node(start, end);
        root.left = buildTree(start, mid);
        root.right = buildTree(mid + 1, end);
        return root;
    }
    private int query(Node node, int end) {
        if (end < node.start) {
            return 0;
        }
        if (end >= node.end) {
            return node.count;
        }
        int mid = node.start + (node.end - node.start) / 2;
        int left = query(node.left, Math.min(mid, end));
        int right = query(node.right, end);
        return left + right;
    }
    private int update(Node node, int val) {
        if (node.start == node.end && node.start == val) {
            node.count += 1;
            return node.count;
        }
        if (val < node.start || val > node.end) {
            return node.count;
        }
        int left = update(node.left, val);
        int right = update(node.right, val);
        node.count = left + right;
        return node.count;
    }
}

Segment Tree Summary

http://www.zhitongguigu.com/

What is segment tree?

Binary Tree
Storing intervals (segments)
Parent cover all children's certain property
Allows querying which of the stored segments contain a given value.

Basic: G4G1, G4G2

Lazy Propagation

CodeForces

Homework 22

http://www.zhitongguigu.com/

Segment Tree

Interval Query

Count of Bigger/Smaller Numbers

Count of Bigger Numbers Before Self [*]

[optional]

The Skyline Problem

Reverse Pairs

Trie Tree

Maximum XOR of Two Numbers in an Array

Add and Search Word - Data structure design

Concatenated Words

[optional]

Word Search II

Palindrome Pairs

Interval Query

http://www.zhitongguigu.com/

Given an integer array of size n as input.

Implement Query and Update methods.

Each query has two integers as index: [start, end]. Return sum between [start end], inclusive.

Each update has two integers as index and value:

[index, val].

Example

Given array A = [1,2,7,8,5].

query(0, 2), return 10.
update(0, 4), change A[0] from 1 to 4.
query(0, 1), return 6.
update(2, 1), change A[2] from 7 to 1.
query(2, 4), return 14.

Count of Smaller/Bigger Numbers

http://www.zhitongguigu.com/

Give you an integer array (index from 0 to n-1, where n is the size of this array, value from 0 to 10000)

Implement

int[] queryBigger(int[]) and int[] querySmaller(int[])

Example

For array [1,2,7,8,5],

queryBigger([1,8,5]), return [4,0,2]

querySmaller([1,8,5,10]), return [0,4,2,5]

[GoValley-201612] Trie & Segment Tree

By govalley201612

[GoValley-201612] Trie & Segment Tree

Introduction to GoValley

1,298

Trie & Segment Tree

Trie Tree (Prefix Tree)

Trie Tree (Prefix Tree)

Trie Tree (Prefix Tree)

Trie Tree (Prefix Tree)

Trie Tree (Prefix Tree)

Trie Tree (Prefix Tree)

Trie Tree (Prefix Tree)

Trie Tree (Prefix Tree)

Trie Tree (Prefix Tree)

Trie Tree (Prefix Tree)

Trie Tree (Prefix Tree)

Word Square

Word Square

Word Square

Word Square

Trie Tree Summary

Segment Tree

Sum of Given Range

Sum of Given Range

Sum of Given Range

Sum of Given Range

Segment Tree

Segment Tree

Min of Given Range

Count of Smaller Numbers After Self

Count of Smaller Numbers After Self

Segment Tree Summary

Homework 22

Interval Query

Count of Smaller/Bigger Numbers

[GoValley-201612] Trie & Segment Tree

More from govalley201612