TSG 強化学習勉強分科会

第6回(第6章後半) TD学習 応用編

@hakatashi

  • 前回の復習

  • アクター・クリティック手法

  • R学習

  • 事後状態

TD学習

  • モンテカルロ法と動的計画法を組み合わせた学習方法
    • エピソードの実際の経験から、(MC法)
    • 隣り合う状態の価値を用いて(DP法)
  • 状態価値関数を更新する。
  • MC法とTD法のどちらが早く収束するかは未解決問題
  • 実際に動かすとTD法のほうが早く収束する場合が多い

基本的なTD学習の種類

  • Sarsa: 方策オン型
  • Q学習: 方策オフ型

  • 前回の復習

  • アクター・クリティック手法

  • R学習

  • 事後状態

アクター・クリティック手法

  • 「価値観数と独立している方策を陽に示す」TD法の学習手法
  • これは、
    • 方策を司る「アクター」と
    • 価値観数を司る「クリティック」
  • の2つのモジュールで構成される

図解

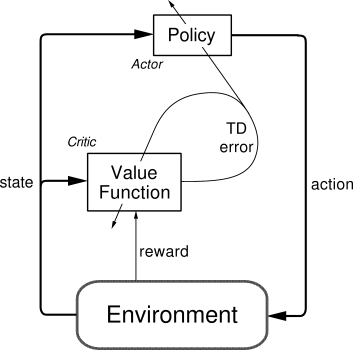
まず、アクターが取った行動をもとに、クリティックは現在の状態価値関数との誤差を計算する。

\delta_{t}=r_{t+1}+\gamma V\left(s_{t+1}\right)-V\left(s_{t}\right)
δt=rt+1+γV(st+1)−V(st)\delta_{t}=r_{t+1}+\gamma V\left(s_{t+1}\right)-V\left(s_{t}\right)

これをTD誤差という。

あるモデルでは、アクターは方策πを決定するのに、行動優先度pというパラメータを保持する。

\pi_{t}\left(s,a\right)=\frac{\mathrm{e}^{p\left(s,a\right)}}{\Sigma_{b}\mathrm{e}^{p\left(s,b\right)}}
πt(s,a)=ep(s,a)Σbep(s,b)\pi_{t}\left(s,a\right)=\frac{\mathrm{e}^{p\left(s,a\right)}}{\Sigma_{b}\mathrm{e}^{p\left(s,b\right)}}

このpはクリティックから与えられるTD誤差によって更新される。更新式はいくつか考えられるが、例えば

p\left(s_{t},a_{t}\right)\leftarrow p\left(s_{t},a_{t}\right)+\beta\delta_{t}\left(1-\pi_{t}\left(s_{t},a_{t}\right)\right)
p(st,at)←p(st,at)+βδt(1−πt(st,at))p\left(s_{t},a_{t}\right)\leftarrow p\left(s_{t},a_{t}\right)+\beta\delta_{t}\left(1-\pi_{t}\left(s_{t},a_{t}\right)\right)

となる。

アクター・クリティック手法の利点

  • 行動選択における計算量が少ない(らしい)
  • 競合的で非マルコフなモデルに対して有効(らしい)

  • 前回の復習

  • アクター・クリティック手法

  • R学習

  • 事後状態

R学習

  • 「割引のない連続タスク」のための学習法
    • 一般に終端状態が存在せず、割引も存在しないタスクを対象とした学習法
    • 単位ステップあたりの報酬の最大化を目指す

R学習の価値関数

R学習では以下のように「ステップあたりの平均期待報酬」として方策の価値を定義する。

\rho^{\pi}=\lim_{n\rightarrow\infty}\frac{1}{n}\sum_{t=1}^{n}E_{\pi}\left\{ r_{t}\right\}
ρπ=limn→∞1n∑t=1nEπ{rt}\rho^{\pi}=\lim_{n\rightarrow\infty}\frac{1}{n}\sum_{t=1}^{n}E_{\pi}\left\{ r_{t}\right\}

次にこのρとの差を用いて状態と行動の価値を定義する。

\tilde{V}^{\pi}\left(s\right)=\sum_{k=1}^{\infty}E_{\pi}\left\{ r_{t+k}-\rho^{\pi}|s_{t}=s\right\}
V~π(s)=∑k=1∞Eπ{rt+k−ρπ∣st=s}\tilde{V}^{\pi}\left(s\right)=\sum_{k=1}^{\infty}E_{\pi}\left\{ r_{t+k}-\rho^{\pi}|s_{t}=s\right\}

これらの価値関数は平均期待報酬に対して相対的に定義されるので、相対報酬と呼ばれる。

R学習ではこの相対報酬に収束するように状態価値を更新することによって学習する。

\tilde{Q}^{\pi}\left(s,a\right)=\sum_{k=1}^{\infty}E_{\pi}\left\{ r_{t+k}-\rho^{\pi}|s_{t}=s,a_{t}=a\right\}
Q~π(s,a)=∑k=1∞Eπ{rt+k−ρπ∣st=s,at=a}\tilde{Q}^{\pi}\left(s,a\right)=\sum_{k=1}^{\infty}E_{\pi}\left\{ r_{t+k}-\rho^{\pi}|s_{t}=s,a_{t}=a\right\}

  • 前回の復習

  • アクター・クリティック手法

  • R学習

  • 事後状態

「最適な行動」とは何か?

  • ここまで、最適な方針(行動の選択)を決定するための指標として、行動価値関数を学習することを進めてきた。
  • しかし、一部のモデルにおいてはより効率的な指標を設けることができる。

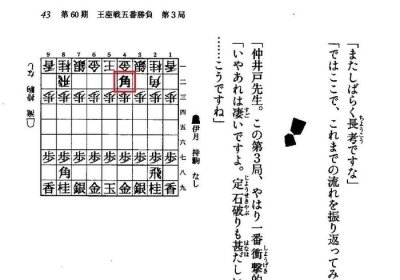
三目並べ

  • 第1章で紹介されている「三目並べ」の例では、エージェントは自分が行動した直後の盤面の状態を予測することができる。
    • ただし、次にどのような状態に遷移するかはわからない。なぜなら相手がどんな手を打つかは予測できないからである。
  • このような場合、その行動の価値は、「直後の盤面の状態」に完全に依存し、その盤面に至るのにどんな状態からどんな行動を取ったかは関係しない。
    • このような状態を事後状態という。

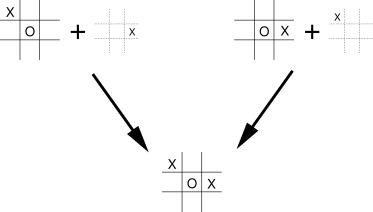
三目並べ

  • 事後状態を考えることができるダイナミクスにおいては、事後状態価値関数を考えることによって、計算量を削減することができる。
    • このようなケースはゲームに多く見られるが、それ以外にも多くのケースで事後状態を考えることができる。
    • まあ、自分の行動の直後の結果が予測できるのはわりと普通のことなので……

おしまい

TSG 強化学習勉強分科会 第6回(第6章後半) TD学習 応用編

By Koki Takahashi

Made with Slides.com

TSG 強化学習勉強分科会 第6回(第6章後半) TD学習 応用編

10/30 TSG 強化学習勉強分科会 第6回 発表スライド

  • 1,973

More from Koki Takahashi