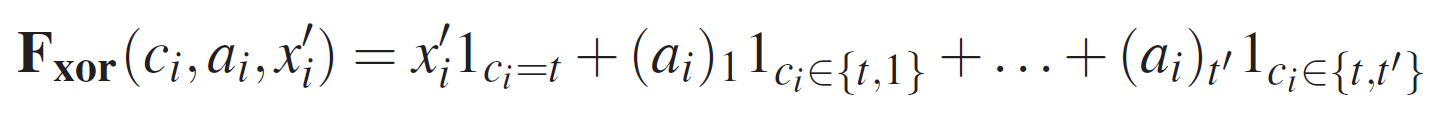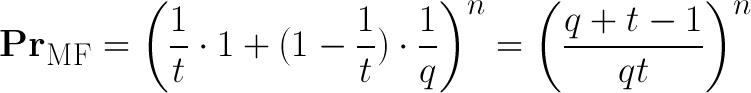The SKI Protocols
A Distance Bounding RFID Protocol Family
[Boureanu-Mitrokotsa-Vaudenay 2013]
Han Tüzün
Bilkent University
Outline
• What is RFID?
• Attacks
• What is Distance-Bounding Protocols
• Phases of DB RFID Protocols
• Existing Protocols
• The SKI Protocols
• Overview of the SKI Protocols
• Variations of the SKI
• Security Analysis of the SKI
• My Critic
• References
What is RFID?
Radio-frequency identification
Used in:
• Passports
• National ID Cards
• Touch-Free Payment
• Identification
• Automatic Pass Systems
• Wireless Car Locks
Attacks
• Relay Attack
• Mafia-Fraud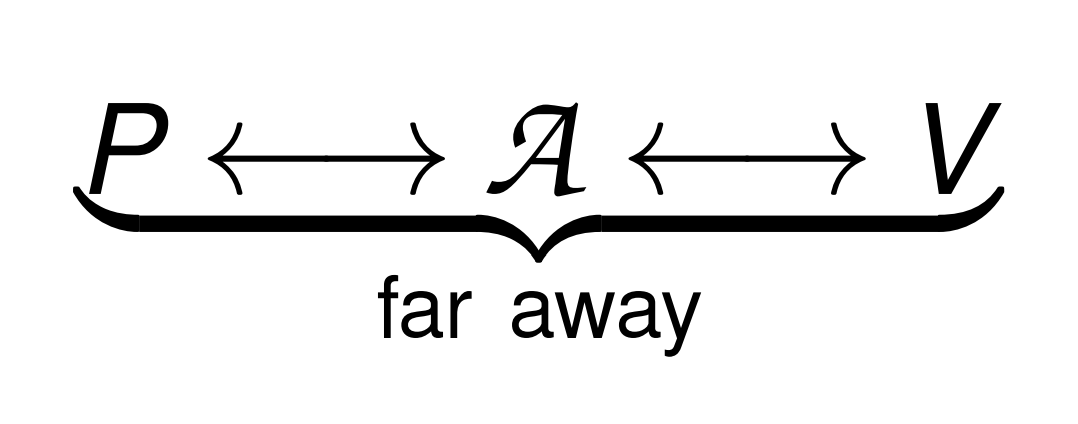
• Distance-Fraud
• Terrorist-Fraud
Relay Attack
Grand Master Chess Problem
Mafia-Fraud
an adversary A tries to prove that
a prover P is close to a verifier V
Mafia-Fraud
Distance-Fraud
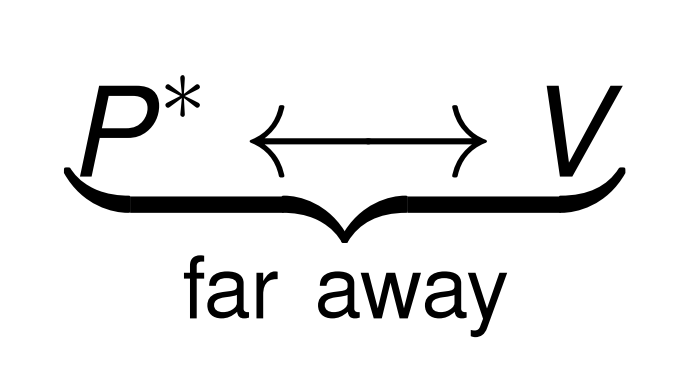
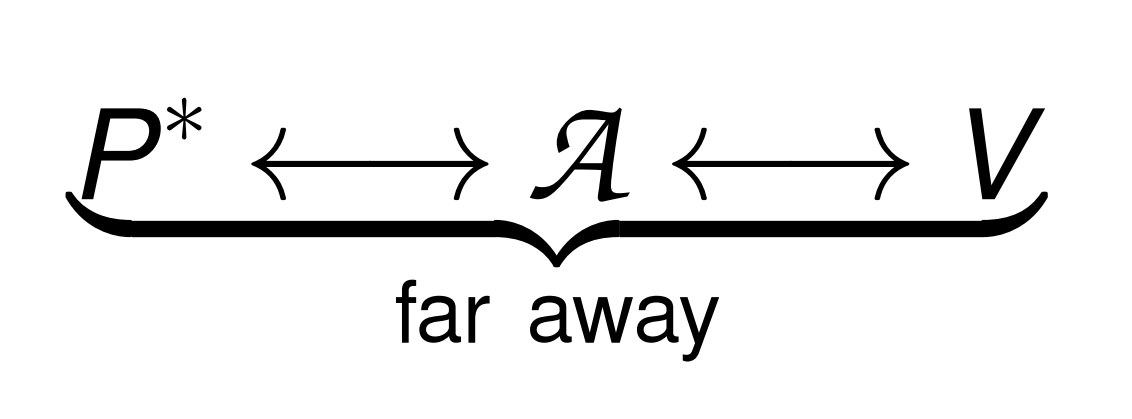
a malicious prover P* tries to prove that
he is close to a verifier V
Distance-Fraud
Terrorist-Fraud
a malicious prover P* helps an adversary A to prove that
P* is close to a verifier V
without giving A another advantage
Terrorist-Fraud
alibinetwork.net
What is Distance-Bounding RFID Protocols?
DBP = authentication + distance upper-bounding
Cryptographic protocols that enable a verifier V
to establish an upper bound
on the pysical distance to a prover P
Rasmussen & Capkun, 2010
Phases of DB RFID Protocols
Slow Transmission Phase(s):
Identification
Varible exchangeSignature exchange
Fast Phase:
Timing the delay between sending out a challenge
and receiving back the corresponding response
Popular DB RFID Protocols
• Hancke & Kuhn (2005)
• Swiss-Knife Protocol (2008)
• Avione et al. (2011)
Hancke & Kuhn (2005)
How to cope with TF?
• P* helps T
• P* does not give her key to T
Aim:
• If P* shares too many information with T,
the protocol must reveal the key of P*
• For a honest P, the protocol
must not reveal the key
The SKI Protocols
Overview of the SKI Protocols
• Pre-shared keys
• One slow phase
• Has variations
• Data transfer other than bits in fast phase
• Possible use of linear mapping on the key
Variables q , t and t'
q
: Size of the responses domain
t : Size of the challenges domain
t' : Security parameter
(Maximum number of registers that can be shared securely)
Linear Transformation ( ℒ )
- Protection against a TF by Hackne
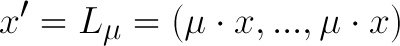
- In SKI, the adversary can get to learn L(x) + e
The Response-Function F
for i = 1 to n, i-th response produced by the following F:
where c
i
∈ {1, . . . , t}, x′
i
∈ GF(q), q ≥ 2,
(a
i
)
j
∈ GF(q),
j ∈ {1, . . . , t′}, and
1R
is 1 if R
is true and 0 otherwise.
Variations of the SKI Protocols
q, t, t', F, ℒ
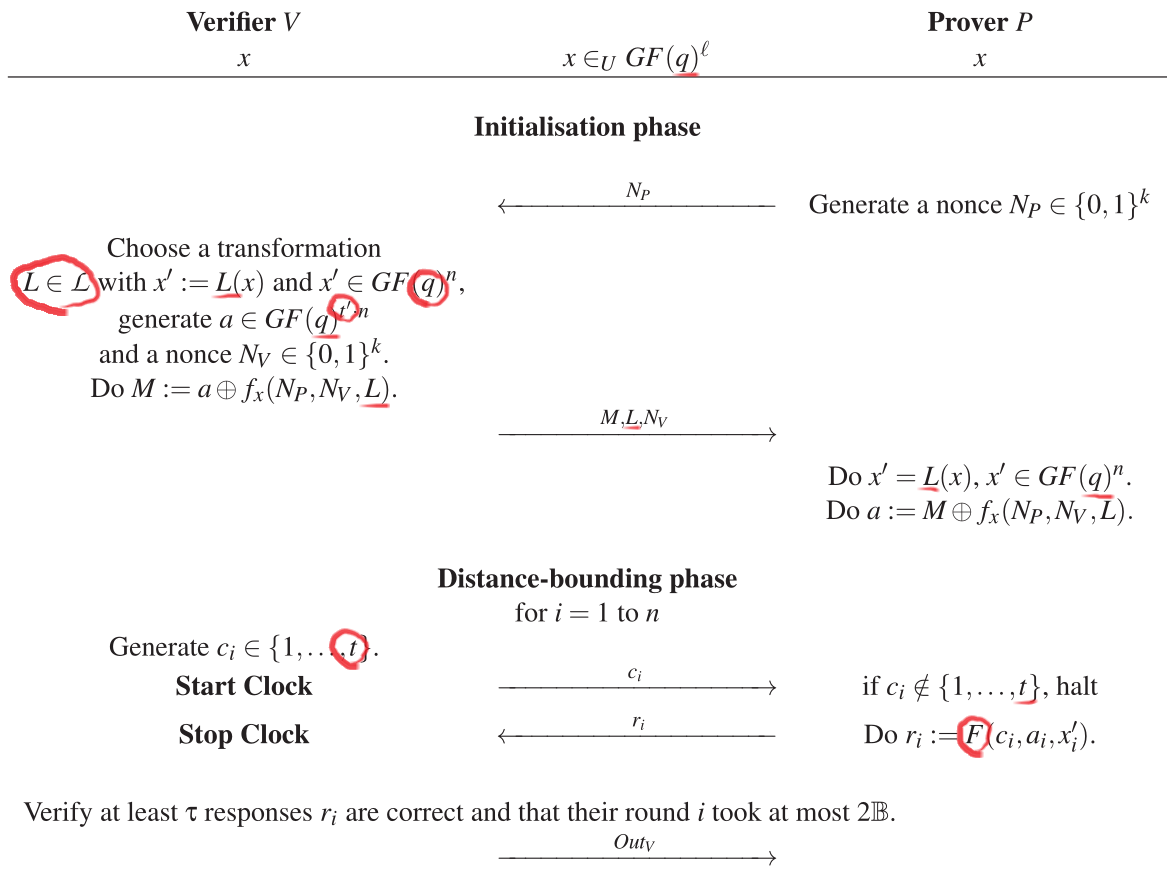
SKI pro
q =
2,
t
=
3
,
t'
=
2
, i.e.,
F(c
i
, a
i
,
x'
i
) = (a
i
)
c
i
for c
i
ϵ
{1, 2}
F(3, a
i
, x'
i
) = x'
i
+
(a
i
)
1
+
(a
i
)
2
, with
(a
i
)
1
,
(a
i
)
2
,
x
i
ϵ
GF(2), and
ℒ = ℒ
bit
SKI lite
q = 2, t = t' = 2 , i.e.,
F(c i , a i , x' i ) = (a i ) c i for c i ϵ {1, 2} with
(a i ) 1 , (a i ) 2 ϵ GF(2), and
ℒ = Ø
Security Analysis of the SKIpro
• Framework for Security Analysis
•
Impersonation?
• Distance-Fraud Resistance
• Mafia-Fraud
Resistance
• Terrorist-Fraud Resistance
Impersonation?
an adversary A tries to prove that
a prover P is close to a verifier V
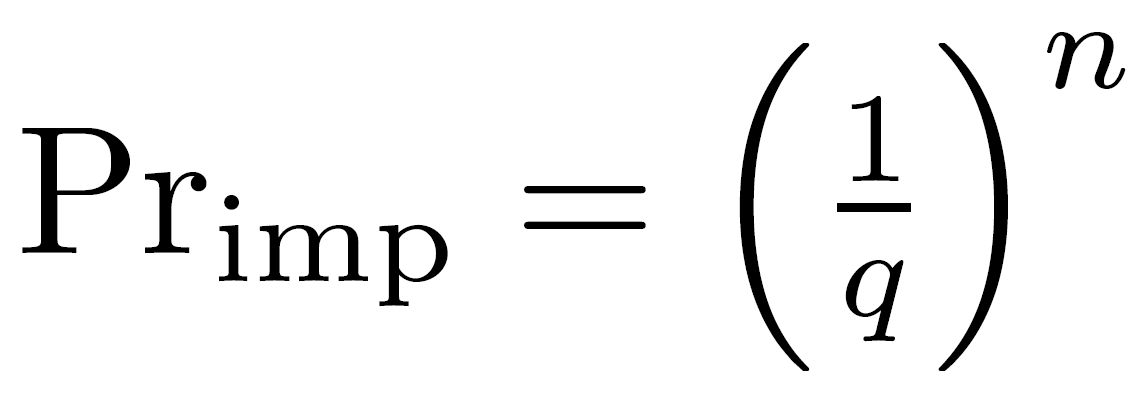
Distance-Fraud Scheme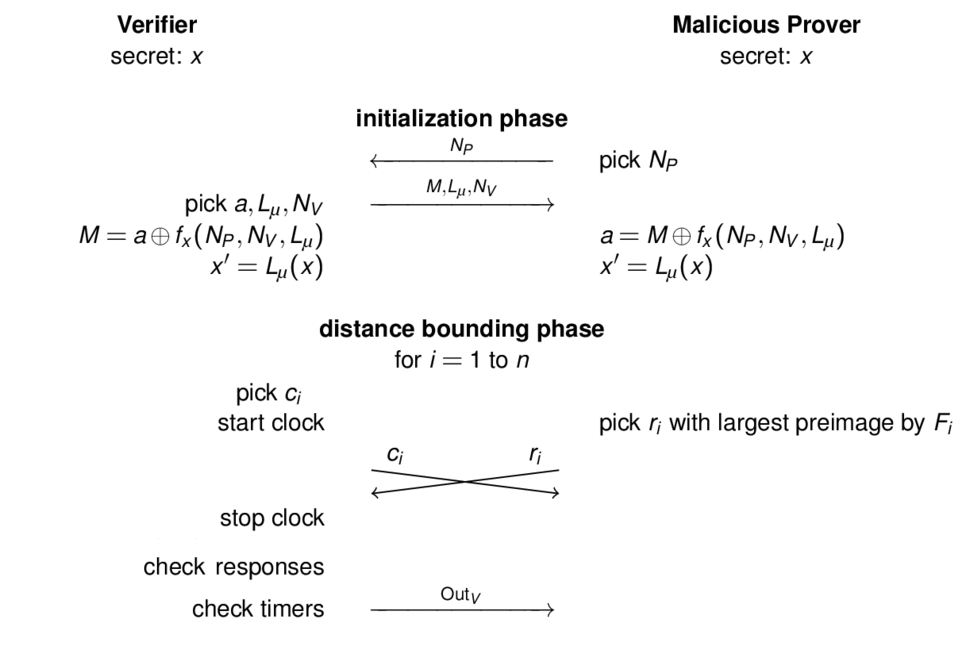
Distance-Fraud Probability
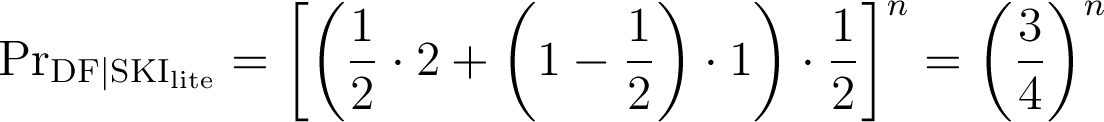
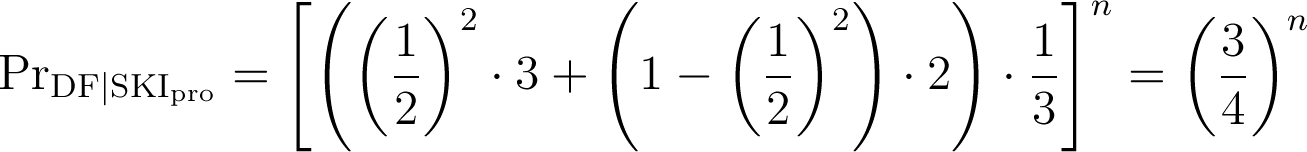
Mafia-Fraud Scheme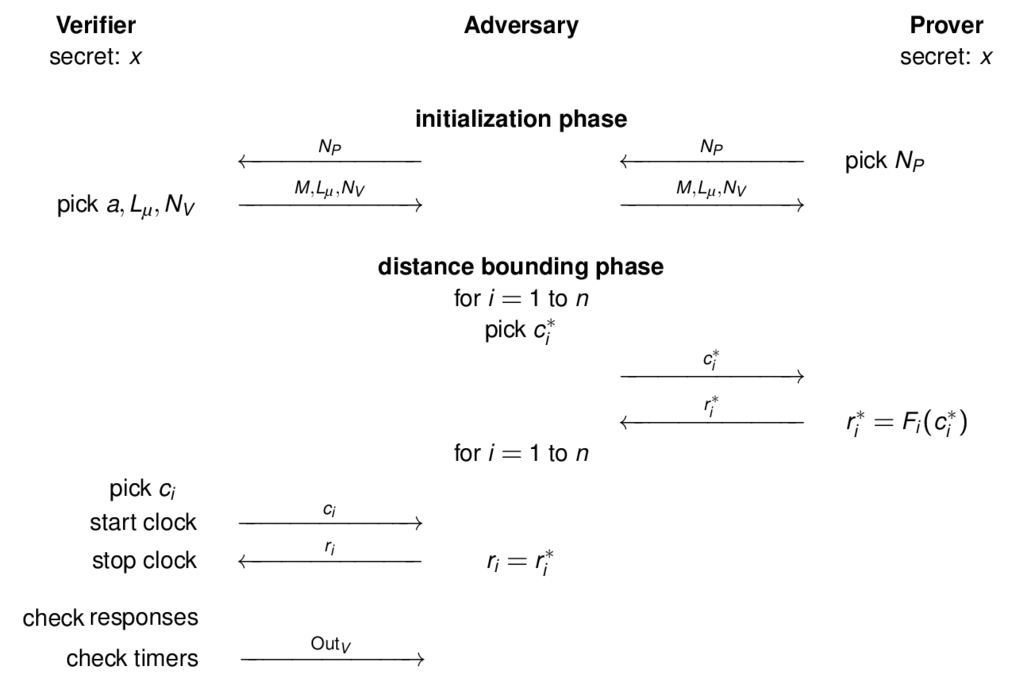
Mafia-Fraud Probability
Terrorist-Fraud Scheme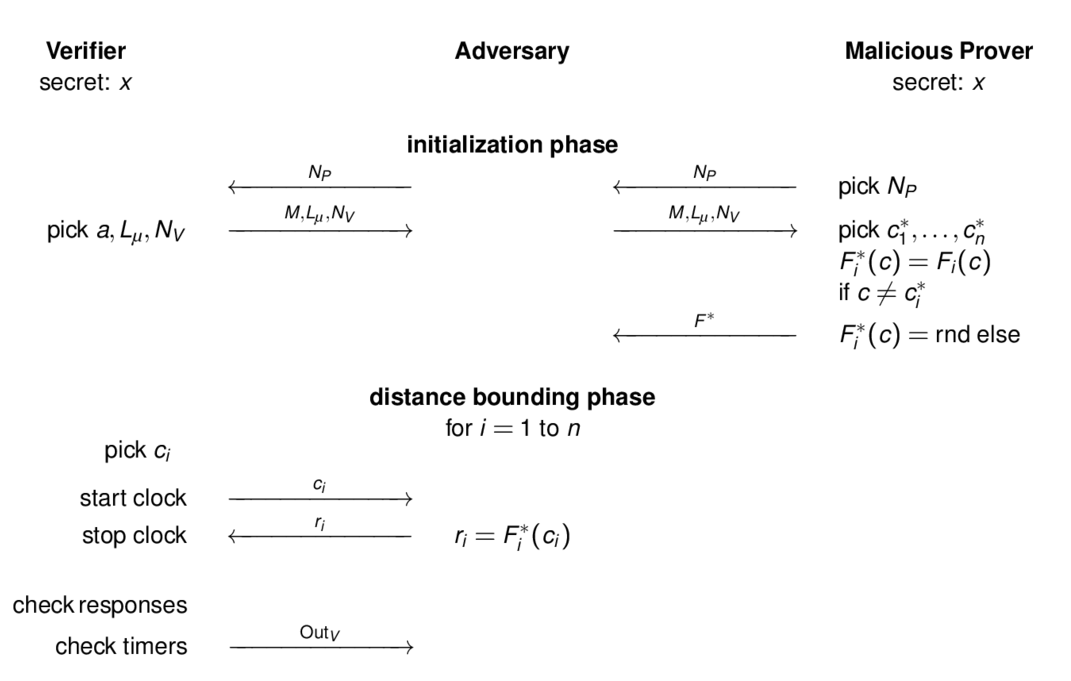
Terrorist-Fraud Probability
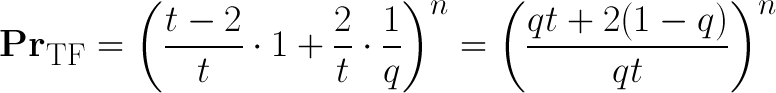
Terrorist-Fraud by Hancke
- Choose a noise-vector e of Hamming weight n - Ƭ
- Provide a slightly modified table ci-> F(ci, ai, xi) :
- if ei = 1, then F(ci, ai, xi) is flipped
- else, do not change the output of F
- Response challenge
- Reconstruct x + e
- In SKI, the adversary can get to learn L(x) + e
My Opinions
• Hard implementation of protocols with q > 2
• A powerful SKI version is not analysed
• Insufficient visualization
References
- Bourenau, Mitrokosta, Vaudenay (2013). Secure & Lightweight Distance Bounding
- Bourenau, Mitrokosta, Vaudenay (2013). Towards Secure Distance Bounding
- Vaudenay (2012). On the Need for Provably Secure Distance Bounding
- Avoine, Bingöl, Kardas, Lauradoux, Martin (2011). A Framework for Analyzing RFID Distance Bounding Protocols
- Avione, Lauradoux, Martin (2011). How Secret-sharing can Defeat Terrorist Fraud
-
Lauradoux (2011). Distance Bounding Protocols and Terrorist Fraud
Thank You
Any Questions?
The SKI Protocol
By Han Tuzun
