Sperner's Lemma in Fair Division
Harshit Yadav
Nikhil Sumer
Rajat Agrawal
Fair division is the problem of dividing a set of goods or resources between several people who have an entitlement to them, such that each person receives his/her due share. This problem arises in various real-world settings:
- auctions
- electronic spectrum and frequency allocation
- airport traffic management, etc.
- The mathematical fair division problem is an idealization of those real life problems. The theory of fair division provides explicit criteria for various different types of fairness.
- Its aim is to provide procedures to achieve a fair division, or prove their impossibility, and study the properties of such divisions both in theory and in real life.
Rental harmony
- The problem of dividing a set of heterogeneous and undesirable items is called fair chore division (if the chores are divisible) or chore assignment (if they are not).
- The problem of dividing a divisible, heterogeneous and desirable resource is called fair cake-cutting.
- We have studied the proof of Sperner's lemma which is a combinatorial analogue of Brouwer's Fixed point Theorem.
- We have also studied the problem of envy free division of a cake using Sperner's lemma.
- Finally we studied the rental harmony theorem which can be seen as a generalization of fair chore division and fair cake cutting problems.
What is the rental harmony theorem?
Suppose n housemates in an n-bedroom house seek
to decide who gets which room and for what part of the total rent. Then assuming a few conditions, the rental harmony theorem states that there exists a partition of the rent so that each person prefers a different
room.
Sperner's Lemma
Sperner's lemma states that every Sperner labelling (described below) of a triangulation of an n-dimensional simplex contains a cell labelled with a complete set of labels.
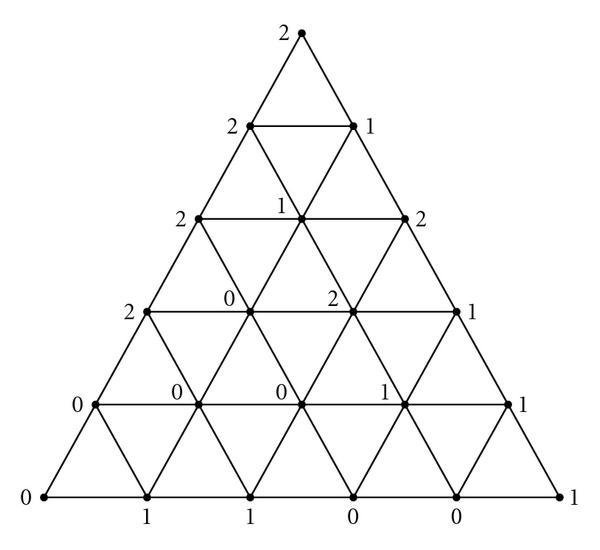
Envy free cake cutting
- We assume the cake to be a rectangular in shape with total length 1. Then for n players, we consider n-1 cuts to divide the cake into n parts whose sum is 1.
- The space S of possible partitions naturally forms a standard (n − 1)-simplex in R^n.
Cake Cutting
- Consider the example of division into 3 parts.
- Label the triangle such that all sub-triangles have all the labels different.
- Go to each vertex, and ask the owner of that vertex, “Which piece would you choose if the cake were cut with this cut-set?”
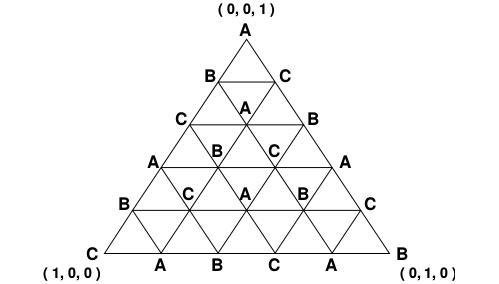
Cake Cutting
- Label that vertex by the number of the piece that is desired.
- This way we obtain a Sperner labelling.
- By Sperner’s lemma, there must be a (1,2,3) - elementary simplex in the triangulation.

Cake Cutting
- Since every such simplex arose from an ABC triangle, this means that we have found 3 very similar cut-sets in which different people choose different pieces of cake.
- Carry out this procedure for a sequence of finer and finer triangulations, each time yielding smaller and smaller (1, 2, 3)-triangles.

Cake Cutting
- By compactness of the triangle and decreasing size of the triangles, there must be a convergent subseque- -nce of triangles converging to a single point.
- Such a point corresponds to a cut-set in which the players are satisfied with different pieces.

- This procedure can be easily generalized for n-players case where we use Barycentric subdivision in order to achieve the triangulation.
- A constructive e-approximate algorithm is obtained by choosing a small enough e (such as the level of the crumbs.
- In this case, we start the the procedure mentioned before with triangulation mesh size less than e.
Chores and rent partitioning
Finding schemes for envy-free chore division has historically been a more complicated problem than cake-cutting. Most envy-free procedures for cake-cuttingdo not carry over to chore division without significant modifications.
We now give a simpler e-approximate algorithm for chore division, which falls out nicely as a special case
of the rent-partitioning problem.
We prove the following theorem using Sperner's Lemma.

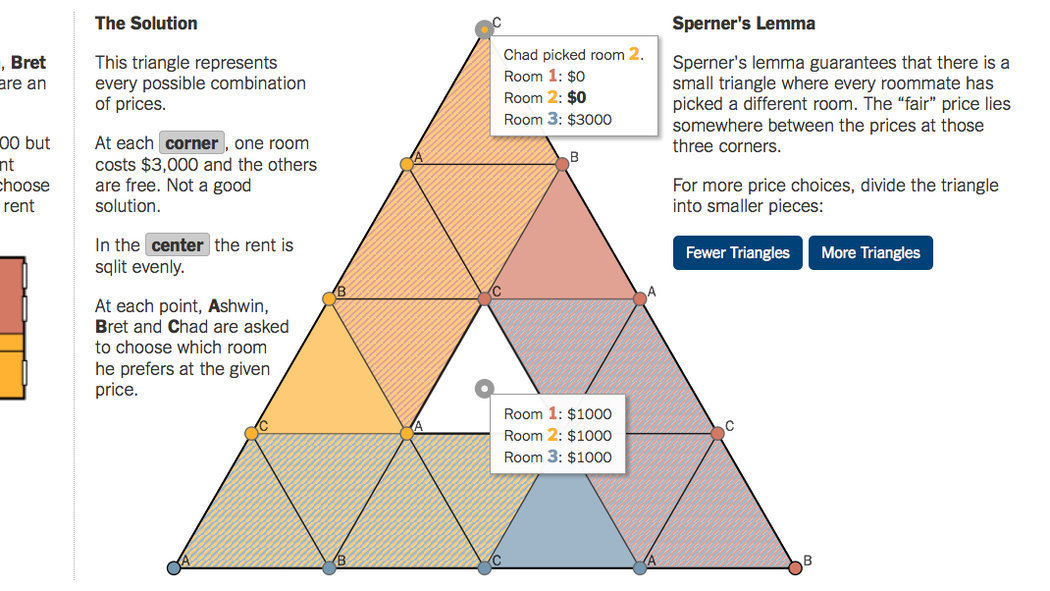
Rental Harmony Theorem
Rental Harmony Theorem
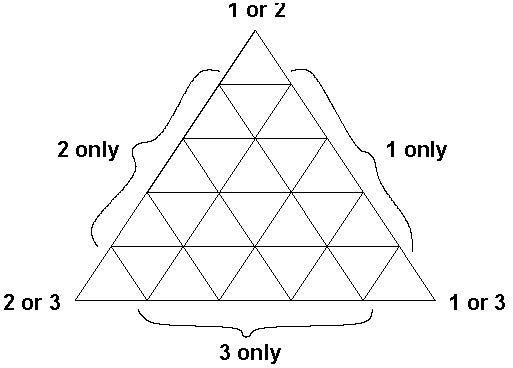
- In this case we obtain a different type of labelling as shown in the figure.
- This is not a Sperner's labelling.
- However, one can prove the existence of a fully labelled simplex on the interior by appealing directly to Sperner’s lemma.
The key idea is to dualize
the simplex S to form a new simplex S* .
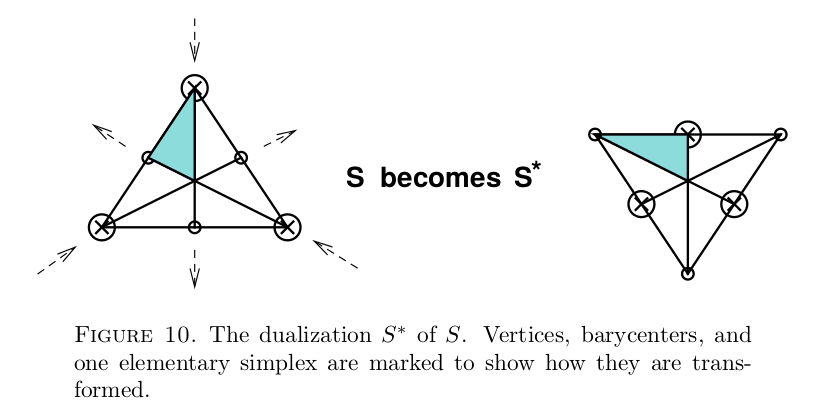
- Now, S* can be triangulated using the labelling inherited form S. The new labelling is a Sperner's labelling.
- Hence there exists a fully labelled elementary simplex of S* , which corresponds to a fully labelled elementary simplex of S, as desired.
- Now, we choose an e smaller than the rental difference for which housemates wouldn’t care.
- We again follow the same procedure as before to obtain an approximate solution.
Thank You
deck
By harshit11y
deck
- 286


