Nonlinear mixed-effects models

Houssein Assaad

Senior Statistician and Software Developer

StataCorp LLC

French Stata UGM, Paris

06 July 2017

Outline

  • What are nonlinear mixed-effects models ? Why and when you should use them ?
  • Exploring the syntax
  • Covariance Structures: A Pharmacokinetics example
  • Multilevel specification (If time allows)
  • Summary
  •  Hierarchical nonlinear models
  • A continuous response evolves nonlinearly over time (or other condition) within individuals from a population of interest
  • Nonlinear models are often based on a model for the mechanism producing the response. As a consequence, the model parameters in a nonlinear model generally have a natural physical interpretation.
  • Nonlinear mixed-effects models (NLME), also known as:
  •  Multilevel nonlinear models
  • Popular in agricultural, environmental, and biomedical applications. For example, NLME models have been used in drug absorption in the body, intensity of earthquakes, and growth of plants.

...First, an existential question:

Why would you want to use NLME models ?

Why nonlinear ?

Why mixed-effects ?

h_t = \frac{\beta_1}{1+\exp{\left\{-\left(t - \beta_2\right)/\beta_3\right\}}}
ht=β11+exp{−(t−β2)/β3}h_t = \frac{\beta_1}{1+\exp{\left\{-\left(t - \beta_2\right)/\beta_3\right\}}}

Let \(h_t\) be the expected height of a tree at time \(t\) which is modelled using a logistic growth model

  • \(\beta_1\) is the asymptotic height as \(t\to\infty\)

Why nonlinear ?

  • \(\beta_3\) is the time it takes for a tree to grow from 50% to about 73% of  \( \beta_1\)

     

  • \(\beta_2\) is the time at which the tree reaches half of its asymptotic height
h_t \approx -2.3 + 16.6t -44.4t^2 + 56.8t^3-31.5t^4+6.3t^5
ht≈−2.3+16.6t−44.4t2+56.8t3−31.5t4+6.3t5h_t \approx -2.3 + 16.6t -44.4t^2 + 56.8t^3-31.5t^4+6.3t^5
h_t = \frac{3}{1+\exp{\left\{-\left(t - 1\right)/.2\right\}}}
ht=31+exp{−(t−1)/.2}h_t = \frac{3}{1+\exp{\left\{-\left(t - 1\right)/.2\right\}}}
  • The logistic curve

is approximated very well

in the interval \([0.4, 1.6]\) by the \(5^{th}\) degree polynomial

  • Polynomial approximation is unreliable outside the original interval.
  • Suppose you have a dataset of tree heights measured over time

Why nonlinear ?

  • Interpretability : Coefficients in polynomial model do not have any physical interpretation (e.g. what is the interpretation of the coefficient of \(t^4\) ?)
  • Parsimony : Linear polynomial model uses twice as many parameters as the nonlinear model (logistic model)
  • Validity beyond the observed range of the data
  +---------------------+
  |   id      X       Y |
  |---------------------|
  |    1     14     5.6 |
  |    1     21     9.6 |
  |    1     42    15.5 |
  |---------------------|
  |    2     15    12.6 |
  |    2     21    16.4 |
  |    2     42    16.9 |
  |    2     51    18.9 |
  +---------------------+
\texttt{Y}_{42}
Y42\texttt{Y}_{42}
\texttt{Y}_{31}
Y31\texttt{Y}_{31}
\texttt{Y}_{12}
Y12\texttt{Y}_{12}
\texttt{Y}_{ij} = \frac{\beta_1}{1+\exp{\left(\texttt{X}_{ij} - \beta_2\right)/\beta_3}} + \epsilon_{ij}
Yij=β11+exp(Xij−β2)/β3+ϵij\texttt{Y}_{ij} = \frac{\beta_1}{1+\exp{\left(\texttt{X}_{ij} - \beta_2\right)/\beta_3}} + \epsilon_{ij}
  • Data consists of \(j=1,\ldots,N\) subjects, each measured \(n_j\) times
\texttt{Y}_{11}
Y11\texttt{Y}_{11}

Why mixed-effects ?

  • \(\beta_1\), \(\beta_2\), and \(\beta_3\) may be subject-specific, e.g.
\beta_1 = \beta_{1j} = b_1 + U_j
β1=β1j=b1+Uj\beta_1 = \beta_{1j} = b_1 + U_j

fixed effect

random effect

+
++

mixed effect

where

\epsilon_{ij}\sim N\left(0, \sigma^2\right)
ϵij∼N(0,σ2)\epsilon_{ij}\sim N\left(0, \sigma^2\right)
U_{j}\sim N\left(0, \sigma^2_u\right)
Uj∼N(0,σu2)U_{j}\sim N\left(0, \sigma^2_u\right)

where

Why mixed effects ?

  • Observations within the same subject are correlated
  • Mixed-effects models allow us to account for the correlation of \(Y_{sj}\) and \(Y_{tj}\) by including in our model  a random effect \(U_j\) specific to \(j^{th}\) subject
  • The inclusion of random effects allow the parameters of interest (e.g. asymptotic growth ) to have subject-specific interpretations. Very important in pharmacokinetics, for example, where the goal is to derive dosage regimen for a specific patient.
\mathtt{cov}\left(Y_{sj}, Y_{tj}\right) \neq 0
cov(Ysj,Ytj)≠0\mathtt{cov}\left(Y_{sj}, Y_{tj}\right) \neq 0

2 observations on \(j^{th}\) subject

The Stata 15 menl command

Exploring the syntax

Fun example: Unicorn health study in Zootopia

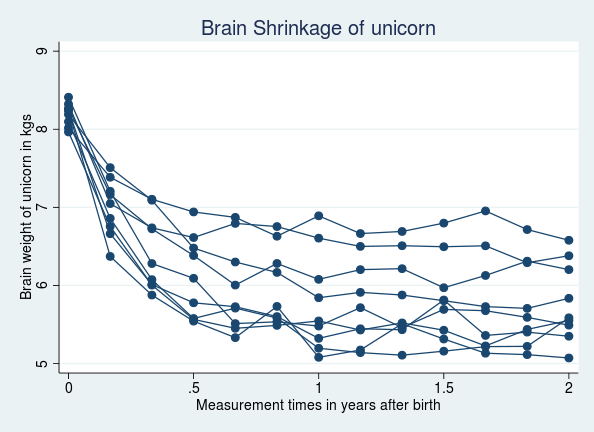
. webuse unicorn
(Brain shrinkage of unicorns in the land of Zootopia)

. twoway connected weight time if id < 10, connect(L) ///
	title(Brain Shrinkage of unicorn)
  • Based on previous studies, a model for unicorn brain shrinkage is believed to be
\texttt{weight}_{ij} = \beta_1 + \left(\beta_2 - \beta_1\right)\exp\left(-\beta_3\texttt{time}_{ij}\right) + \epsilon_{ij}
weightij=β1+(β2−β1)exp(−β3timeij)+ϵij\texttt{weight}_{ij} = \beta_1 + \left(\beta_2 - \beta_1\right)\exp\left(-\beta_3\texttt{time}_{ij}\right) + \epsilon_{ij}

where \(\epsilon_{ij}\sim N\left(0,\sigma^2\right)\)

  • \(\beta_1\) is average asymptotic brain weight of unicorns as \(\texttt{time}_{ij} \to \infty\)
  • \(\beta_2\) is average brain weight at birth (at \(\texttt{time}_{ij} = 0 \))
  • \(\beta_3\) is a scale parameter that determines the rate at which the average brain weight approaches the asymptotic weight \(\beta_1\) (decay rate)
\texttt{weight}_{ij} = \beta_1 + \left(\beta_2 - \beta_1\right)\exp\left(-\beta_3\texttt{time}_{ij}\right) + \epsilon_{ij}
weightij=β1+(β2−β1)exp(−β3timeij)+ϵij\texttt{weight}_{ij} = \beta_1 + \left(\beta_2 - \beta_1\right)\exp\left(-\beta_3\texttt{time}_{ij}\right) + \epsilon_{ij}
  • We assume the asymptotic weight \(\beta_1\) is unicorn-specific (varies across unicorns) by including a random effect \(U_j\) as follows
\beta_1 = \beta_{1j} = b_1 + U_j,
β1=β1j=b1+Uj,\beta_1 = \beta_{1j} = b_1 + U_j,
  • Thus our model may be written as
\texttt{weight}_{ij} = b_1 + U_j + \left\{\beta_2 - \left(b_1 + U_j\right)\right\}\exp\left(-\beta_3\texttt{time}_{ij}\right) + \epsilon_{ij}
weightij=b1+Uj+{β2−(b1+Uj)}exp(−β3timeij)+ϵij\texttt{weight}_{ij} = b_1 + U_j + \left\{\beta_2 - \left(b_1 + U_j\right)\right\}\exp\left(-\beta_3\texttt{time}_{ij}\right) + \epsilon_{ij}
U_j \sim N\left(0, \sigma^2_u\right)
Uj∼N(0,σu2)U_j \sim N\left(0, \sigma^2_u\right)
. menl weight = {b1}+{U[id]} + ({beta2} - ({b1}+{U[id]}) )*exp(-{beta3}*time)
  • Here is how you can fit it with 

(Output is on next slide)

menl
\beta_{1j}
β1j\beta_{1j}
\beta_{1j}
β1j\beta_{1j}

gsem-like syntax

. menl weight = {b1}+{U[id]} + ({beta2} - ({b1}+{U[id]}) )*exp(-{beta3}*time)

Obtaining starting values by EM:

Alternating PNLS/LME algorithm:

Iteration 1:    linearization log likelihood = -56.9757597

Computing standard errors:

Mixed-effects ML nonlinear regression           Number of obs     =        780
Group variable: id                              Number of groups  =         60

                                                Obs per group:
                                                              min =         13
                                                              avg =       13.0
                                                              max =         13
Linearization log likelihood =  -56.97576
------------------------------------------------------------------------------
      weight |      Coef.   Std. Err.      z    P>|z|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
         /b1 |   4.707954   .1414511    33.28   0.000     4.430715    4.985193
      /beta2 |   8.089432   .0260845   310.12   0.000     8.038307    8.140556
      /beta3 |    4.13201   .0697547    59.24   0.000     3.995293    4.268726
------------------------------------------------------------------------------

------------------------------------------------------------------------------
  Random-effects Parameters  |   Estimate   Std. Err.     [95% Conf. Interval]
-----------------------------+------------------------------------------------
id: Identity                 |
                      var(U) |   1.189809   .2180058      .8308328    1.703887
-----------------------------+------------------------------------------------
               var(Residual) |   .0439199   .0023148      .0396095    .0486995
------------------------------------------------------------------------------
\texttt{weight}_{ij} = b_1 + U_j + \left\{\beta_2 - \left(b_1 + U_j\right)\right\}\exp\left(-\beta_3\texttt{time}_{ij}\right) + \epsilon_{ij}
weightij=b1+Uj+{β2−(b1+Uj)}exp(−β3timeij)+ϵij\texttt{weight}_{ij} = b_1 + U_j + \left\{\beta_2 - \left(b_1 + U_j\right)\right\}\exp\left(-\beta_3\texttt{time}_{ij}\right) + \epsilon_{ij}
. menl weight = {b1}+{U[id]} + ({beta2} - ({b1}+{U[id]}) )*exp(-{beta3}*time)
  • We could have used the two-stage formulation of our model
\texttt{weight}_{ij} = \beta_1 + \left(\beta_2 - \beta_1\right)\exp\left(-\beta_3\texttt{time}_{ij}\right) + \epsilon_{ij}
weightij=β1+(β2−β1)exp(−β3timeij)+ϵij\texttt{weight}_{ij} = \beta_1 + \left(\beta_2 - \beta_1\right)\exp\left(-\beta_3\texttt{time}_{ij}\right) + \epsilon_{ij}
\beta_1 = \beta_{1j} = b_1 + U_j
β1=β1j=b1+Uj\beta_1 = \beta_{1j} = b_1 + U_j
. menl weight = {beta1:} + ({beta2} - {beta1:})*exp({beta3}*time),
> define(beta1: {b1}+{U[id]})
  • Particularly useful for more complicated models
  • Parameters specified within                  may be easily predicted after estimation
define()

Incorporating covariates

  • \(\texttt{cupcake}\) : number of cupcakes consumed right after birth
  • \(\texttt{female}\) :     \(\texttt{female}_j\) is \(1\) if the \(j\)th unicorn is a female and \(0\) otherwise
  • Reducing brain weight loss has been an active research area in Zootopia, and scientists believe that consuming rainbow cupcakes right after birth may help slow down brain shrinkage.
\beta_{3j} = b_{30} + b_{31}\mathtt{cupcake}_j
β3j=b30+b31cupcakej\beta_{3j} = b_{30} + b_{31}\mathtt{cupcake}_j
  • Also, we would like to investigate whether the asymptote, \(\beta_{1j}\), is gender specific, so we include the factor variable \(\mathtt{female}\) in the equation for \(\beta_{1j}\).
\beta_{1j} = b_{10} + b_{11}\mathtt{female}_j + U_{1j}
β1j=b10+b11femalej+U1j\beta_{1j} = b_{10} + b_{11}\mathtt{female}_j + U_{1j}
define(beta3: {b30} + {b31}*cupcake)
define(beta1: {b10} + {b11}*1.female + {U[id]})

decay rate

. menl weight = {beta1:} + ({beta2:} - {beta1:})*exp(-{beta3:}*time),
> define(beta1: {b10}+{b11}*1.female+{U0[id]})
> define(beta2: {b2})
> define(beta3: {b30}+{b31}*cupcake)

Mixed-effects ML nonlinear regression           Number of obs     =        780
Group variable: id                              Number of groups  =         60

                                                Obs per group:
                                                              min =         13
                                                              avg =       13.0
                                                              max =         13
Linearization log likelihood = -29.014988

        beta1:  {b10}+{b11}*1.female+{U0[id]}
        beta2:  {b2}
        beta3:  {b30}+{b31}*cupcake

------------------------------------------------------------------------------
      weight |      Coef.   Std. Err.      z    P>|z|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
        /b10 |   4.072752   .1627414    25.03   0.000     3.753785     4.39172
        /b11 |   1.264407   .2299723     5.50   0.000     .8136694    1.715144
         /b2 |   8.088102   .0255465   316.60   0.000     8.038032    8.138172
        /b30 |   4.706926   .1325714    35.50   0.000      4.44709    4.966761
        /b31 |  -.2007309   .0356814    -5.63   0.000    -.2706651   -.1307966
------------------------------------------------------------------------------

------------------------------------------------------------------------------
  Random-effects Parameters  |   Estimate   Std. Err.     [95% Conf. Interval]
-----------------------------+------------------------------------------------
id: Identity                 |
                     var(U0) |   .7840578   .1438924      .5471839    1.123473
-----------------------------+------------------------------------------------
               var(Residual) |   .0420763   .0022176      .0379468    .0466551
------------------------------------------------------------------------------

  • Based on our results, consuming rainbow cupcakes after birth indeed slows down brain shrinkage: \(\mathtt{/b31}\) is roughly \(-0.2\) with a 95% \(\mathtt{CI}\) of \([-.27, -.13]\)

Useful shortcut for your nonlinear expression

define(beta3: {b30} + {b31}*cupcake + {b32}*juice + {U2[id]})
define(beta3: cupcake juice U2[id])
define(beta3: {b30} + {b31}*cupcake)
define(beta3: cupcake, xb)
  • What if you have many covariates ?

Summary I

  • Model parameters and random effects are bound in braces if specified directly in the expression: $$\texttt{\{b0\}}, \texttt{\{U0[id]\}} \text{, etc}.$$
  • Linear combinations of variables can be included using the specification

 

  • Random effects can be specified within a linear combination, in which case they should be included without curly braces, for example, $$\texttt{\{lc u: x1 x2 U[id]\}}$$

e.g., 

\texttt{\{lc: x1 x2, noconstant\}}
{lc: x1 x2, noconstant}\texttt{\{lc: x1 x2, noconstant\}}
\texttt{\{eqname:varlist [ , xb noconstant ]\}}
{eqname:varlist [ , xb noconstant ]}\texttt{\{eqname:varlist [ , xb noconstant ]\}}
\texttt{\{beta: mpg weight i.rep78\}}
{beta: mpg weight i.rep78}\texttt{\{beta: mpg weight i.rep78\}}

and

  • Random-effects names must start with a capital letter as in

    \(\texttt{\{U0[id]\}}\)

Pharmacokinetics (PK) study of Theophylline

  • Pharmacokinetics is  the study of “what the body does with a drug”
  • PK seeks to understand how drugs enter the body, distribute throughout the body, and leave the body, by summarizing concentration-time measurements, while accounting for patient-specific characteristics.

     

  • Maintain drug concentrations within the therapeutic window
  • Consider data on the antiasthmatic agent theophylline (Boeckmann, Sheiner, and Beal [1994] 2011).
  • The drug was administrated orally to \(12\) subjects with the dosage (mg/kg) given on a per weight basis.
  • Serum concentrations (in mg/L) were obtained at \(11\) time points per subject over \(25\) hours following administration.
. webuse theoph

. twoway connected conc time, connect(L)
  • Clearance (\(\mathtt{Cl}\)) measures the rate at which a drug is cleared from the plasma. It is defined as the volume of plasma cleared of drug per unit time.
  • Elimination rate constant (\(k_e\)) describes the rate at which a drug is removed from the body. It is defined as the fraction of drug in the body eliminated per unit time.
  • Absorption rate constant (\(k_a\)) describes the rate at which a drug is absorbed by the body.
\texttt{conc}_{ij} = \frac{\texttt{dose}_j k_{e} k_{a_j}}{\mathtt{Cl}_j\left(k_{a_j} - k_{e}\right)}\times
concij=dosejkekajClj(kaj−ke)×\texttt{conc}_{ij} = \frac{\texttt{dose}_j k_{e} k_{a_j}}{\mathtt{Cl}_j\left(k_{a_j} - k_{e}\right)}\times
\left\{\exp\left(-k_{e}\texttt{time}_{ij}\right)-\exp\left(-k_{a_j}\texttt{time}_{ij}\right)\right\} + \epsilon_{ij}
{exp(−ketimeij)−exp(−kajtimeij)}+ϵij\left\{\exp\left(-k_{e}\texttt{time}_{ij}\right)-\exp\left(-k_{a_j}\texttt{time}_{ij}\right)\right\} + \epsilon_{ij}
\texttt{conc}_{ij} = \frac{\texttt{dose}_j k_{e} k_{a_j}}{\mathtt{Cl}_j\left(k_{a_j} - k_{e}\right)}\times
concij=dosejkekajClj(kaj−ke)×\texttt{conc}_{ij} = \frac{\texttt{dose}_j k_{e} k_{a_j}}{\mathtt{Cl}_j\left(k_{a_j} - k_{e}\right)}\times
\left\{\exp\left(-k_{e}\texttt{time}_{ij}\right)-\exp\left(-k_{a_j}\texttt{time}_{ij}\right)\right\} + \epsilon_{ij}
{exp(−ketimeij)−exp(−kajtimeij)}+ϵij\left\{\exp\left(-k_{e}\texttt{time}_{ij}\right)-\exp\left(-k_{a_j}\texttt{time}_{ij}\right)\right\} + \epsilon_{ij}

Because each of the model parameters must be positive to be meaningful, we write

\mathtt{Cl}_j = \exp\left(\beta_0 + U_{0j}\right)
Clj=exp(β0+U0j)\mathtt{Cl}_j = \exp\left(\beta_0 + U_{0j}\right)
k_{a_j} = \exp\left(\beta_1 + U_{1j}\right)
kaj=exp(β1+U1j)k_{a_j} = \exp\left(\beta_1 + U_{1j}\right)
k_{e} = \exp\left(\beta_2\right)
ke=exp(β2)k_{e} = \exp\left(\beta_2\right)

(Output is on next slide)

. menl conc =(dose*{ke:}*{ka:}/({cl:}*({ka:}-{ke:})))* 
>            (exp(-{ke:}*time)-exp(-{ka:}*time)), 
> define(cl: exp({b0}+{U0[subject]}))         
> define(ka: exp({b1}+{U1[subject]}))        
> define(ke: exp({b2})) 

Mixed-effects ML nonlinear regression           Number of obs     =        132
Group variable: subject                         Number of groups  =         12

                                                Obs per group:
                                                              min =         11
                                                              avg =       11.0
                                                              max =         11
Linearization log likelihood = -177.02233

          cl:  exp({b0}+{U0[subject]})
          ka:  exp({b1}+{U1[subject]})
          ke:  exp({b2})

------------------------------------------------------------------------------
        conc |      Coef.   Std. Err.      z    P>|z|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
         /b0 |  -3.227212   .0600089   -53.78   0.000    -3.344827   -3.109597
         /b1 |   .4656357   .1985941     2.34   0.019     .0763984     .854873
         /b2 |  -2.454679   .0524896   -46.77   0.000    -2.557556   -2.351801
------------------------------------------------------------------------------

------------------------------------------------------------------------------
  Random-effects Parameters  |   Estimate   Std. Err.     [95% Conf. Interval]
-----------------------------+------------------------------------------------
subject: Independent         |
                     var(U0) |    .027864   .0121371      .0118652    .0654355
                     var(U1) |   .4143467   .1945672       .165067    1.040082
-----------------------------+------------------------------------------------
               var(Residual) |   .5030242   .0688883      .3846079    .6578995
------------------------------------------------------------------------------

covariance(U1 U2 U3, unstructured)
  • By default, menl assumes that all random effects are independent, thus, in the previous model, we have assumed that \(\text{cov}\left(U_{0}, U_{1}\right) = 0\), but we could have considered other covariance structures for the random effects
\Sigma = \begin{bmatrix}\sigma^2_{1} & \sigma_{12} & \sigma_{13} \\ \sigma_{12} & \sigma^2_{2} & \sigma_{23} \\ \sigma_{13} & \sigma_{23} & \sigma^2_{3}\end{bmatrix}
Σ=[σ12σ12σ13σ12σ22σ23σ13σ23σ32]\Sigma = \begin{bmatrix}\sigma^2_{1} & \sigma_{12} & \sigma_{13} \\ \sigma_{12} & \sigma^2_{2} & \sigma_{23} \\ \sigma_{13} & \sigma_{23} & \sigma^2_{3}\end{bmatrix}
U_1
U1U_1
U_2
U2U_2
U_3
U3U_3
U_1
U1U_1
U_2
U2U_2
U_3
U3U_3
  • For example, when there are 3 random effects \(U_1\), \(U_2\), and \(U_3\) in the model, their covariance structure may be summarized as
\text{cov}\left(U_{1}, U_{3}\right)
cov(U1,U3) \text{cov}\left(U_{1}, U_{3}\right)
\text{var}\left( U_{1}\right)
var(U1) \text{var}\left( U_{1}\right)
\Sigma = \begin{bmatrix}\sigma_{11} & \sigma_{12} & \sigma_{12} \\ & \sigma_{11} & \sigma_{12} \\ & & \sigma_{11}\end{bmatrix}
Σ=[σ11σ12σ12σ11σ12σ11] \Sigma = \begin{bmatrix}\sigma_{11} & \sigma_{12} & \sigma_{12} \\ & \sigma_{11} & \sigma_{12} \\ & & \sigma_{11}\end{bmatrix}
covariance(U*, exchangeable)
covariance(U*, identity)
\Sigma = \begin{bmatrix}\sigma_{11} & 0 & 0 \\ & \sigma_{11} & 0 \\ & & \sigma_{11}\end{bmatrix}
Σ=[σ1100σ110σ11] \Sigma = \begin{bmatrix}\sigma_{11} & 0 & 0 \\ & \sigma_{11} & 0 \\ & & \sigma_{11}\end{bmatrix}
\Sigma = \begin{bmatrix}\sigma_{11} & 0 & 0 \\ 0 & \sigma_{22} & \sigma_{23} \\ 0 & \sigma_{23} & \sigma_{33}\end{bmatrix}
Σ=[σ11000σ22σ230σ23σ33] \Sigma = \begin{bmatrix}\sigma_{11} & 0 & 0 \\ 0 & \sigma_{22} & \sigma_{23} \\ 0 & \sigma_{23} & \sigma_{33}\end{bmatrix}
covariance(U2 U3, unstructured)
  • Other examples of random effects covariance structures are:
U_1
U1U_1
U_2
U2U_2
U_3
U3U_3
. menl conc =(dose*{ke:}*{ka:}/({cl:}*({ka:}-{ke:})))* 
>            (exp(-{ke:}*time)-exp(-{ka:}*time)), 
> define(cl: exp({b0}+{U0[subject]}))         
> define(ka: exp({b1}+{U1[subject]}))        
> define(ke: exp({b2})) covariance(U*, unstructured)
  • Going back to our PK model, we may wish to assume that \(U_{0j}\) and \(U_{1j}\) have a general covariance matrix
U_1
U1U_1
U_2
U2U_2
U_3
U3U_3
. menl conc =(dose*{ke:}*{ka:}/({cl:}*({ka:}-{ke:})))* 
>            (exp(-{ke:}*time)-exp(-{ka:}*time)), 
> define(cl: exp({b0}+{U0[subject]}))         
> define(ka: exp({b1}+{U1[subject]}))        
> define(ke: exp({b2})) covariance(U*, unstructured)

Linearization log likelihood = -177.02222

          cl:  exp({b0}+{U0[subject]})
          ka:  exp({b1}+{U1[subject]})
          ke:  exp({b2})

--------------------------------------------------------------------------------
          conc |      Coef.   Std. Err.      z    P>|z|     [95% Conf. Interval]
---------------+----------------------------------------------------------------
           /b0 |  -3.227224   .0600072   -53.78   0.000    -3.344836   -3.109612
           /b1 |   .4656428   .1985911     2.34   0.019     .0764113    .8548742
           /b2 |  -2.454696   .0524895   -46.77   0.000    -2.557574   -2.351819
--------------------------------------------------------------------------------

------------------------------------------------------------------------------
  Random-effects Parameters  |   Estimate   Std. Err.     [95% Conf. Interval]
-----------------------------+------------------------------------------------
subject: Unstructured        |
                     var(U0) |   .0278616   .0121451      .0118566    .0654714
                     var(U1) |   .4143347    .194565      .1650595    1.040069
                  cov(U0,U1) |  -.0002056   .0332183     -.0653122    .0649011
-----------------------------+------------------------------------------------
               var(Residual) |   .5030238   .0688885      .3846073    .6578995
------------------------------------------------------------------------------
  • Combine resvariance()     and rescorrelation()      to build flexible covariance structures.
  • Use option resvariance()     to model heteroskedasticity as a linear, power, or exponential function of other covariates or of predicted values.
  • Use option rescorrelation()      to model the dependence of the within-group errors as, e.g., AR or MA processes.
  • menl provides flexible modeling of within-group error or residual covariance structures.

So far, we have assumed that \(\text{Var}\left(\epsilon_{ij}\right) = \sigma^2\) and \(\text{cov}\left(\epsilon_{sj}, \epsilon_{tj}\right)=0\)

menl
resvariance()
rescorrelation()
resvariance()
rescorrelation()
\text{Var}\left(\epsilon_{ij}\right) = \sigma^2\left\{\left(\hat{\texttt{conc}}_{ij}\right)^{\delta} + c\right\}^2
Var(ϵij)=σ2{(conc^ij)δ+c}2\text{Var}\left(\epsilon_{ij}\right) = \sigma^2\left\{\left(\hat{\texttt{conc}}_{ij}\right)^{\delta} + c\right\}^2
resvariance(power _yhat)
  • For example, heteroskedasticity, often present in PK data, is modeled using the power function plus a constant.

 

Adding a constant avoids the variance of zero at \(\texttt{time}_{ij}\) = 0, because the concentration is zero at that time.

 

  • We will also use restricted maximum likelihood estimation (REML) via option            instead of the default maximum likelihood (ML) estimation to account for a moderate number of subjects.
reml
. menl conc =(dose*{ke:}*{ka:}/({cl:}*({ka:}-{ke:})))*
>        (exp(-{ke:}*time)-exp(-{ka:}*time)),
> define(cl: exp({b0}+{U0[subject]}))
> define(ka: exp({b1}+{U1[subject]}))
> define(ke: exp({b2}))
> resvariance(power _yhat) reml

Mixed-effects REML nonlinear regression         

Linear. log restricted-likelihood = -172.44384

          cl:  exp({b0}+{U0[subject]})
          ka:  exp({b1}+{U1[subject]})
          ke:  exp({b2})

------------------------------------------------------------------------------
        conc |      Coef.   Std. Err.      z    P>|z|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
         /b0 |  -3.227295   .0619113   -52.13   0.000    -3.348639   -3.105951
         /b1 |   .4354519   .2072387     2.10   0.036     .0292716    .8416322
         /b2 |  -2.453743   .0517991   -47.37   0.000    -2.555267   -2.352218
------------------------------------------------------------------------------

------------------------------------------------------------------------------
  Random-effects Parameters  |   Estimate   Std. Err.     [95% Conf. Interval]
-----------------------------+------------------------------------------------
subject: Independent         |
                     var(U0) |   .0316416    .014531      .0128634    .0778326
                     var(U1) |   .4500585   .2228206      .1705476    1.187661
-----------------------------+------------------------------------------------
Residual variance:           |
  Power _yhat                |
                      sigma2 |   .1015759    .086535      .0191263    .5394491
                       delta |   .3106636   .2466547     -.1727707    .7940979
                       _cons |   .7150935   .3745256      .2561837    1.996063
------------------------------------------------------------------------------


. predict (Cl = {cl:})

. list subject Cl if subject[_n]!=subject[_n-1], sep(0) noobs

  +--------------------+
  | subject         Cl |
  |--------------------|
  |       1   .0274995 |
  |       2   .0402322 |
  |       3   .0406919 |
  |       4   .0371865 |
  |       5   .0425807 |
  |       6   .0461769 |
  |       7   .0466375 |
  |       8   .0442402 |
  |       9   .0324682 |
  |      10   .0356245 |
  |      11   .0510018 |
  |      12     .03785 |
  +--------------------+
  • We can predict the clearance parameter \(\mathtt{Cl}_j\) for each subject
  • Interpretation: For subject 1, \(0.027\) liters of serum concentration are cleared of the theophylline drug per hour per kg body weight.
  • In other words,  if subject 1 weighs 75 kg, \(75\times0.027 \approx 2\) liters of serum concentration are cleared of theophylline every hour

Summary II

y_{ij} = \mathtt{func}\left(\texttt{covariates}, {\beta}_j\right) + \epsilon_{ij}
yij=func(covariates,βj)+ϵijy_{ij} = \mathtt{func}\left(\texttt{covariates}, {\beta}_j\right) + \epsilon_{ij}

Stage I:

\beta_{j} = \mathtt{func}\left(\texttt{covariates}, \mathbf b, \mathbf U_j\right)
βj=func(covariates,b,Uj)\beta_{j} = \mathtt{func}\left(\texttt{covariates}, \mathbf b, \mathbf U_j\right)

Stage II:

menl y = <menlexpr>, define() [define() ...]
covariance(U1 U2 [U3 ...], <covtype>)
resvariance() rescorrelation()

with

\mathbf U_j = \left(U_{0j},U_{1j},\ldots,U_{qj}\right) \sim \mathtt{MVN}\left(\mathbf 0, \Sigma\right)
Uj=(U0j,U1j,…,Uqj)∼MVN(0,Σ)\mathbf U_j = \left(U_{0j},U_{1j},\ldots,U_{qj}\right) \sim \mathtt{MVN}\left(\mathbf 0, \Sigma\right)
\left(\epsilon_{1j}, \ldots ,\epsilon_{n_jj}\right) \sim \mathtt{MVN}\left(\mathbf 0, \sigma^2 \Lambda_j\right)
(ϵ1j,…,ϵnjj)∼MVN(0,σ2Λj)\left(\epsilon_{1j}, \ldots ,\epsilon_{n_jj}\right) \sim \mathtt{MVN}\left(\mathbf 0, \sigma^2 \Lambda_j\right)

and

2-stage specification

Single-stage specification

y_{ij} = \mathtt{func}\left(\texttt{covariates}, \mathbf b, \mathbf U_j\right)
yij=func(covariates,b,Uj)y_{ij} = \mathtt{func}\left(\texttt{covariates}, \mathbf b, \mathbf U_j\right)
+ \epsilon_{ij}
+ϵij+ \epsilon_{ij}
menl y = <menlexpr>

What about multilevel NLME models ?

  • Consider fictional data on tree circumference of 30 trees planted in 5 different planting zones.  The tree circumferences were recorded over the period of 1990 to 2003.

Zone 1

Zone 5

Tree 27

Tree 6

Tree 31

Tree 1

Tree 2

\(1990\)

\(1991\)

\(2003\)

Zone 2

Level 3

Level 2

Level 1

  • We wish to fit the 3-parameter logistic growth model:
  • \(\texttt{circum}_{ijt}\) and \(\texttt{age}_{ijt}\) are circumference (cm) and age (in years) of tree \(j\) within planting zone \(i\) in year \(t\)
  • Parameters: Asymptotic circumference (\(\beta_1\)), time at which half of \(\beta_1\) is attained (\(\beta_2\)), and scale parameter (\(\beta_3\))
  • For simplicity we assume that only \(\beta_2\) may be affected by zones and trees-within-zones:
\beta_2 = \beta_{2ij} = b_2 + U_{1i} + U_{2ij}
β2=β2ij=b2+U1i+U2ij\beta_2 = \beta_{2ij} = b_2 + U_{1i} + U_{2ij}
\texttt{circum}_{ijt} = \frac{\beta_1}{1+\exp{\left\{-\left(\texttt{age}_{ijt} - \beta_2\right)/\beta_3\right\}}} + \epsilon_{ijt}
circumijt=β11+exp{−(ageijt−β2)/β3}+ϵijt\texttt{circum}_{ijt} = \frac{\beta_1}{1+\exp{\left\{-\left(\texttt{age}_{ijt} - \beta_2\right)/\beta_3\right\}}} + \epsilon_{ijt}
. menl circum = {b1}/(1 + exp(-(age - {beta2:})/{b3})),  
>  define(beta2: {b2} + {U1[zone]} + {U2[zone > tree]})  stddeviations


Mixed-effects ML nonlinear regression           Number of obs     =        420

-------------------------------------------------------------
                |     No. of       Observations per Group
        Path    |     Groups    Minimum    Average    Maximum
----------------+--------------------------------------------
           zone |          5         56       84.0        112
      zone>tree |         30         14       14.0         14
-------------------------------------------------------------

Linearization log likelihood =  313.18701

       beta2:  {b2}+{U1[zone]}+{U2[zone>tree]}

------------------------------------------------------------------------------
     circumf |      Coef.   Std. Err.      z    P>|z|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
         /b1 |   30.01228   .0228861  1311.38   0.000     29.96742    30.05713
         /b2 |   6.459742   .0757833    85.24   0.000     6.311209    6.608274
         /b3 |   2.902458   .0046722   621.21   0.000     2.893301    2.911615
------------------------------------------------------------------------------

------------------------------------------------------------------------------
  Random-effects Parameters  |   Estimate   Std. Err.     [95% Conf. Interval]
-----------------------------+------------------------------------------------
zone: Identity               |
                      sd(U1) |   .1599475    .057271      .0792858    .3226707
-----------------------------+------------------------------------------------
zone>tree: Identity          |
                      sd(U2) |   .1244983   .0178957      .0939312    .1650126
-----------------------------+------------------------------------------------
                sd(Residual) |   .0966751   .0034615      .0901233    .1037034
------------------------------------------------------------------------------
\texttt{circum}_{ijt} = \frac{\beta_1}{1+\exp{\left\{-\left(\texttt{age}_{ijt} - \beta_2\right)/\beta_3\right\}}} + \epsilon_{ijt}
circumijt=β11+exp{−(ageijt−β2)/β3}+ϵijt\texttt{circum}_{ijt} = \frac{\beta_1}{1+\exp{\left\{-\left(\texttt{age}_{ijt} - \beta_2\right)/\beta_3\right\}}} + \epsilon_{ijt}
\beta_2 = \beta_{2ij} = b_2 + U_{1i} + U_{2ij}
β2=β2ij=b2+U1i+U2ij\beta_2 = \beta_{2ij} = b_2 + U_{1i} + U_{2ij}
  • We can predict the time to reach half of the asymptotic circumference  (\(\beta_2\)) for each planting zone \(i\):
. predict (beta2_i = {beta2:}), relevel(zone)

. list zone beta2_i if zone[_n]!=zone[_n-1], sep(0) noobs

  +----------------------------+
  |            zone    beta2_i |
  |----------------------------|
  |     New England   6.357335 |
  |    Mid Atlantic   6.273229 |
  | E North Central   6.723731 |
  | W North Central   6.481954 |
  |  South Atlantic    6.46246 |
  +----------------------------+
\hat{\beta}_2 = \beta_{ij} = \hat{b}_2 + U_{1i} + U_{2ij}
β^2=βij=b^2+U1i+U2ij\hat{\beta}_2 = \beta_{ij} = \hat{b}_2 + U_{1i} + U_{2ij}

Summary

  •            supports ML and REML estimation and provides flexible random-effects and residual covariance structures.

 

  •            supports single-stage and two-stage specifications.

     

  • You can predict random effects and their standard errors, group-specific nonlinear parameters, and more after estimation; see [ME] menl postestimation.

 

  • NLMEs are known to be sensitive to initial values. menl   provides default, but for some models you may need to specify your own. Use option initial().

 

  • NLMEs are known to have difficulty converging or converging to a local maximum. Trying different initial values may help.

 

menl
menl
menl
menl
initial()

ALWAYS BE YOURSELF

UNLESS YOU CAN BE A UNICORN

THEN ALWAYS BE A UNICORN

 

 

Thank You!

deck

By H Assaad

Made with Slides.com

deck

  • 3,052

More from H Assaad