COMP2521
Data Structures & Algorithms
Week 2.2
Abstract Data Types (ADTs)
Author: Hayden Smith 2021
In this lecture
Why?
- ADTs are a fundamental concept of writing robust software, and of being able to work with other people
What?
- ADT definition
- ADT usage
- ADT implementation
ADTs
- Data type:
- Set of values (atomic or structured)
- Collection of operations on those values
Can you think of some examples?
What is a data type?
- int
- set of value(s): an integer
- operations: addition, subtraction, multiplication, etc
- array:
- set of values(s): a repeat of any data type (e.g. int)
- operations: index lookup, index assignment, etc
Abstraction
- Abstraction: Hiding details of a how a system is built in favour of focusing on the high level behaviours, or inputs and outputs, of the system
- Examples?
- C abstracts away assembly/MIPS code.
- Python abstract away pointer arithmetic and memory allocation.
- Web browsers abstract away the underlying hardware that they're run on.
Abstract Data Type
ADT is a description of a data type that focuses on it's high level behaviour, without regard for how it is implemented underneath. This means:
- There is a separation of interface from implementations
- Users of the ADT see only the interface
- Builds of the ADT provide an implementation
- Both parties need to agree on the ADTs interface
- Interface allows people to agree at the start, and work separately.
Programming by Contract
- When we define our interface, we also need to include information about:
- Pre-conditions: What conditions hold at the start of the function call
- Post-conditions: What conditions will hold at the end of the function
- Add them via comments
- Can sanity check with asserts
Abstract Data Type
- Step 1: Determine the interface of your ADT in a .h file
- Step 2: The "developer" builds a concrete implementation for the adt in a .c file
-
Step 3: The "user" uses the abstract data type in their program
- They have to compile with it, even though they might not understand how it is built underneath
Set data type: collection of unique integer values.
What will we figure out first?
- What behaviour does this ADT need? (interface)
How are we going to code for it? (implementation)
Set ADTs
- create an empty collection
- insert one item into the collection
- remove one item from the collection
- find an item in the collection
- check the size of the collection
- drop the entire collection
- display the collection
- check if unions or intersects with another set
Set ADTs
Let's brainstorm!
Now we start to write this as C code!
Notice that we aren't implementing anything yet?
Set ADTs
Set SetCreate() // create a new set
void SetInsert(Set, int) // add number into set
void SetDelete(Set, int) // remove number from set
int SetMember(Set, int) // set membership test
int SetCard(Set) // size of set
Set SetUnion(Set, Set) // union
Set SetIntersect(Set, Set) // intersection
void SetDestroy(Set) // destroy a created setSet ADTs
#ifndef SET_H
#define SET_H
#include <stdio.h>
#include <stdbool.h>
typedef struct SetRep *Set;
// ADT functions go here
#endifThree key principles of ADTs in C:
- The "Set" (or equivalent) is usually a pointer of some sort
- That pointer is usually the first argument in every ADT function, with the exception of the create function
- When we write .h files, we use header guards to prevent re-definition
Notice how we haven't defined "struct SetRep"? That's not our job.
Set.h
Set ADTs
// Set.h ... interface to Set ADT
#ifndef SET_H
#define SET_H
#include <stdio.h>
#include <stdbool.h>
typedef struct SetRep *Set;
Set SetCreate(); // create new empty set
void SetDestroy(Set); // free memory used by set
void SetInsert(Set,int); // add value into set
void SetDelete(Set,int); // remove value from set
bool SetMember(Set,int); // set membership
Set SetUnion(Set,Set); // union
Set SetIntersect(Set,Set); // intersection
int SetCard(Set); // cardinality
// others
Set SetCopy(Set); // make a copy of a set
void ShowSet(Set); // display set on stdout
#endifCompleted Set.h
But what's missing?
Programming by contract
- Pre and post conditions now added.
- Helps both developers and users manage expectations
Set ADTs
// create new empty set
// pre: Integer provided is positive
// post: Valid set returned, set is empty
Set SetCreate();
// add value into set
// pre: Valid set provided
// post: New element "n" is now in set s
void SetInsert(Set s, int newval);
// pre: Valid set provided for s1 and s2
// post: ∀ n ∈ res, n ∈ s1 or n ∈ s2
Set SetUnion(Set s1, Set s2) { ... }
// cardinality
// pre: Valid set provided for s
// post: Response is the number of elements in the set
int SetCard(Set s);Set Usage
- How do we actually work with a set though?
- We write our "main" file, and compile it with the set library that the ADT developer has implemented.
- While we need their .c file to build with, we never need to look at it or make sense of it, because we have the ADT (i.e. .h file)
- In fact, we could even just work with the .o file!
my_set.c
Set.c
my_set.o
Set.o
./my_set
Set.h
Set Usage
#include "Set.h"
#include <stdio.h>
int main() {
Set s = SetCreate();
// Could use Scanf instaed
for (int i = 1; i < 26; i += 2) {
SetInsert(s,i);
}
SetShow(s);
printf("\n");
}testSet1.c
It's time to implement the set! The "user" of our set doesn't need to worry about this.
We will implement 3 different types of sets:
- That uses an unsorted array
- That uses a sorted array
- That uses a linked list
Set Implementation
Set Implementation (Unsorted array)
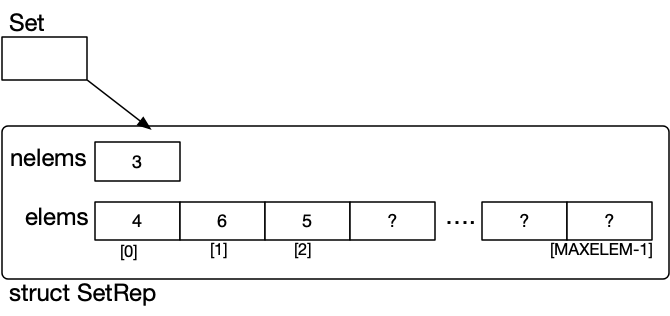
#define MAX_ELEMS 10000
// concrete data structure
struct SetRep {
int elems[MAX_ELEMS];
int nelems;
};
Set SetCreate(int) { ... }
void SetInsert(Set, int) { ... }
void SetDelete(Set, int) { ... }
int SetMember(Set, int) { ... }
int SetCard(Set) { ... }
Set SetUnion(Set, Set) { ... }
Set SetIntersect(Set, Set) { ... }
void SetDestroy(Set) { ... }Set-array.c
We can represent this set using an array (unsorted). This means we do have to do upper and lower bounds checks because there will be a theoretical limit on the size of the set.
A sample of the implemented set
Set Implementation (Unsorted array)
// create new empty set
Set SetCreate()
{
Set s = malloc(sizeof(struct SetRep));
if (s == NULL) {
fprintf(stderr, "Insufficient memory\n");
exit(1);
}
s->nelems = 0;
// assert(isValid(s));
return s;
}
// set membership test
int SetMember(Set s, int n)
{
// assert(isValid(s));
int i;
for (i = 0; i < s->nelems; i++) {
if (s->elems[i] == n) {
return TRUE;
}
}
return FALSE;
}Set Implementation (Unsorted array)
| Data Structure | insert (time) |
delete (time) |
member (time) |
union or intersection (time) |
storage (space) |
|---|---|---|---|---|---|
| unsorted array | O(n) | O(n) | O(n) | O(n * m) | O(E) |
Let's look at the time and space complexities:
- n: Number of elements in the set
- m: Number of elements in another set
- E: Maximum number of items able to be in set
-
Same data structure as for unsorted array. Differences:
- membership test -> can use binary search
- insertion -> binary search and then shift up and insert
- deletion -> binary search and then shift down
Set Implementation (Sorted array)
Set Implementation (Sorted array)
| Data Structure | insert (time) |
delete (time) |
member (time) |
union or intersection (time) |
storage (space) |
|---|---|---|---|---|---|
| unsorted array | O(n) | O(n) | O(n) | O(n * m) | O(E) |
| sorted array | O(n) | O(n) | O(logn) | O(n * m) | O(E) |
Set Implementation (Linked list)
typedef struct Node {
int value;
struct Node *next;
} Node;
struct SetRep {
Node *elems; // pointer to first node
int nelems; // number of nodes
};
Set SetCreate() { ... }
void SetInsert(Set, int) { ... }
void SetDelete(Set, int) { ... }
int SetMember(Set, int) { ... }
int SetCard(Set) { ... }
Set SetUnion(Set, Set) { ... }
Set SetIntersect(Set, Set) { ... }
void SetDestroy(Set) { ... }Set-list.c
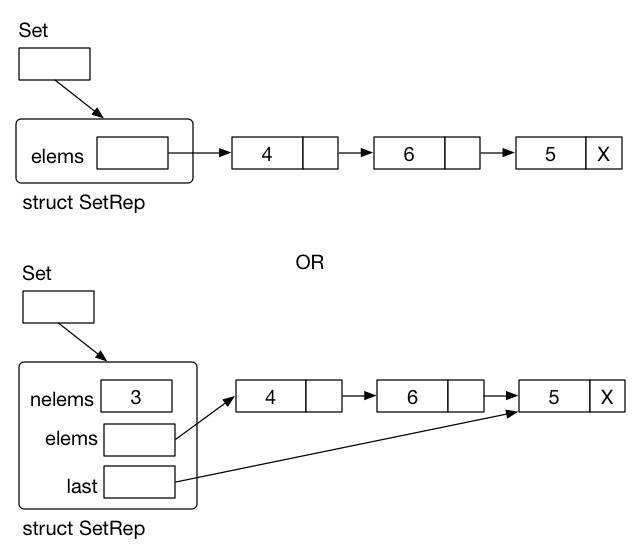
Set Implementation (Linked list)
// create new empty set
Set newSet()
{
Set s = malloc(sizeof(struct SetRep));
if (s == NULL) {...}
s->nelems = 0;
s->elems = s->last = NULL;
return s;
}
// set membership test
int SetMember(Set s, int n)
{
// assert(isValid(s));
Node *cur = s->elems;
while (cur != NULL) {
if (cur->value == n) return true;
cur = cur->next;
}
return false;
}
Set Implementation (Linked list)
| Data Structure | insert (time) |
delete (time) |
member (time) |
union or intersection (time) |
storage (space) |
|---|---|---|---|---|---|
| unsorted array | O(n) | O(n) | O(n) | O(n * m) | O(E) |
| sorted array | O(n) | O(n) | O(logn) | O(n * m) | O(E) |
| unsorted linked list | O(n) | O(n) | O(n) | O(n * m) | O(n) |
Direct access - issues?
What happens if we try to access elements of the implementation directly?
We might receive a "dereferencing pointer to incomplete type" error

ADT Summary
- ADT interface:
- A user-view of the data structure
- Functions for all operations
- Explanations of those operations
- Any guarantees it provides ("Contract")
- ADT implementation:
- Concrete definition of the data structures
- List, tree, graph, array, etc etc
- Definition of functions that operate on the data structure
- Concrete definition of the data structures
- Why abstract the data structure?
- Allows future iterations to remove or upgrade a data structure
- Allows things like lists to actually have more intelligent implementations underneath
ADT Summary
Feedback

COMP2521 21T2 - 2.2 - Abstract Data Types (ADTs)
By haydensmith
COMP2521 21T2 - 2.2 - Abstract Data Types (ADTs)
- 1,347



