COMP2521
Data Structures & Algorithms
Week 5.1
Graph ADT
Author: Hayden Smith 2021
In this lecture
Why?
- Graphs are one of the most general and fundamental data types in software, so let's understand it from an abstract point of view
What?
- Graph Definition
- Graph Examples
- Graph Terminology
- Graph ADT
Graph
A graph G = (V, E) is a general data structure that consists of:
- V: A set of vertices (i.e. a collection of items)
- E: A set of edges (relationships between items)
They may contain cycles, and there is no implicit order of items
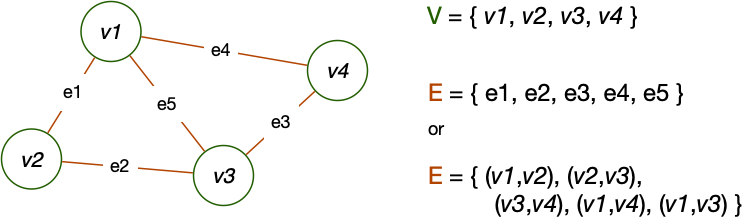
Graph Examples
Graphs are everywhere:
- The internet is a graph (vertices = webpage, edge = links)
- Roads and maps are graphs (vertice = intersections, edge = roads)
-
Trees are graphs (vertices = nodes, edges = children)
- Trees are a special type of graph with no cycles
-
Linked lists are graphs (vertices = nodes, edges = next links)
- Linked lists are a special type of tree with 1 child
Graph Example (Map)
We can turn a map of Australia into a graph quite easily.
| Distance | Adelaide | Brisbane | Canberra | Darwin | Melbourne | Perth | Sydney |
|---|---|---|---|---|---|---|---|
| Adelaide | - | 2055 | 1390 | 3051 | 732 | 2716 | 1605 |
| Brisbane | 2055 | - | 1291 | 3429 | 1671 | 4771 | 982 |
| Canberra | 1390 | 1291 | - | 4441 | 658 | 4106 | 309 |
| Darwin | 3051 | 3429 | 4441 | - | 3783 | 4049 | 4411 |
| Melbourne | 732 | 1671 | 658 | 3783 | - | 3448 | 873 |
| Perth | 2716 | 4771 | 4106 | 4049 | 3448 | - | 3972 |
| Sydney | 1605 | 982 | 309 | 4411 | 873 | 3972 | - |
Graph Example (Map)
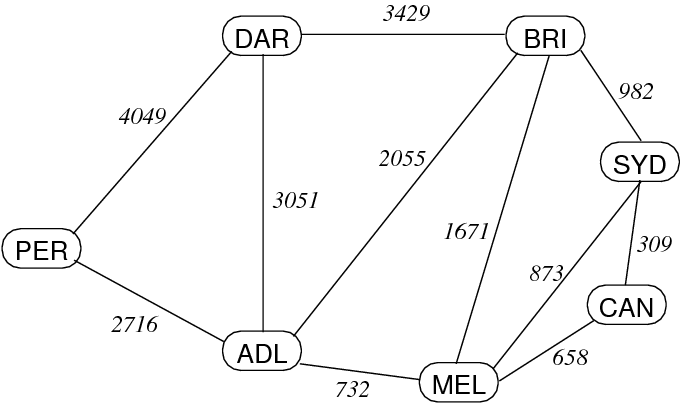
This allows us to ask questions like:
- What cities are connected to Darwin?
- Is there a way to get from Brisbane to Perth?
Graph Terminology
- For neighbours:
- v1 and v2 are adjacent
- a is incident on both v1 and v2
- Degree of a vertex: Number of edges incident
- Vertex = node (same thing)
- Edge = link (same thing)
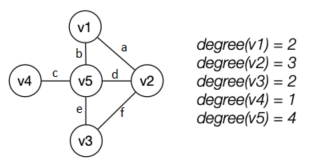
Graph Terminology
- Path: Sequence of vertices where each vertex has an edge to it's predecessor
- Cycle: A path where the last vertex in the path is the same as the first vertex
- Length of path: #edges in it
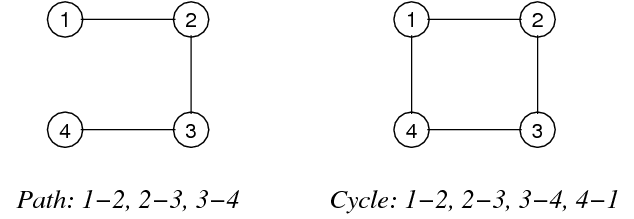
Graph Terminology
-
Connected Graph: There is a path from each vertex to every other vertex
- Most graphs are connected, otherwise they are disjoint
- Complete Graph: There is an edge from each vertex to every other vertex
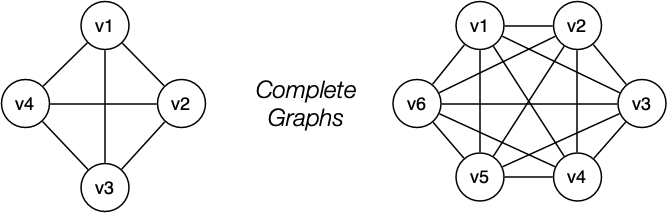
Graph Terminology
- Tree: Connected (sub)graph with no cycles
- Spanning tree: Tree containing all vertices
- Clique: Complete subgraph
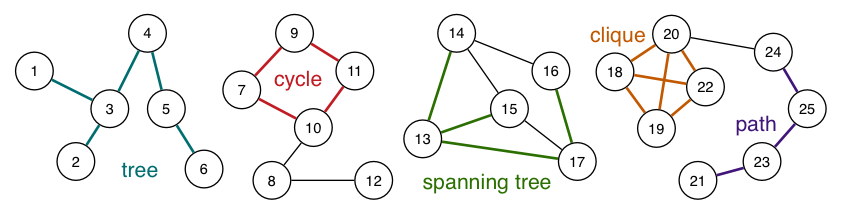
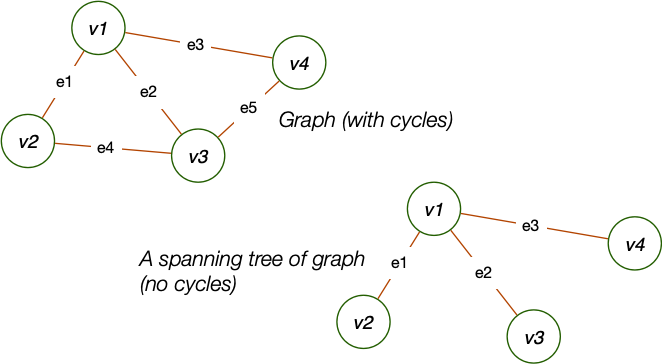
Graph Terminology
-
Spanning tree of connected graph G = (V, E):
- A subgraph of G containing all of V and itself is a single tree (connected, no cycles)
-
Spanning forest of a non-connected graph G = (V, E):
- A subgraph of G containing all of V, and is a set of trees (not connected, no cycles), with one tree for each connected component
Other Graphs
We will look at these, but in later lectures:
- Directed V Undirected graph
- Weighted V Unweighted graph
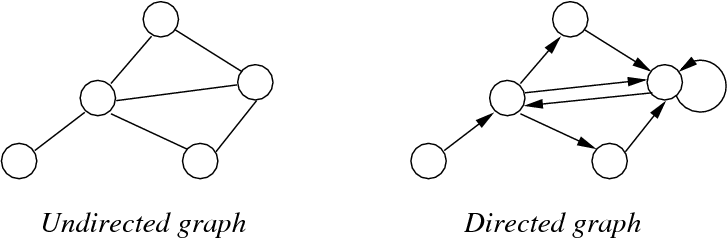
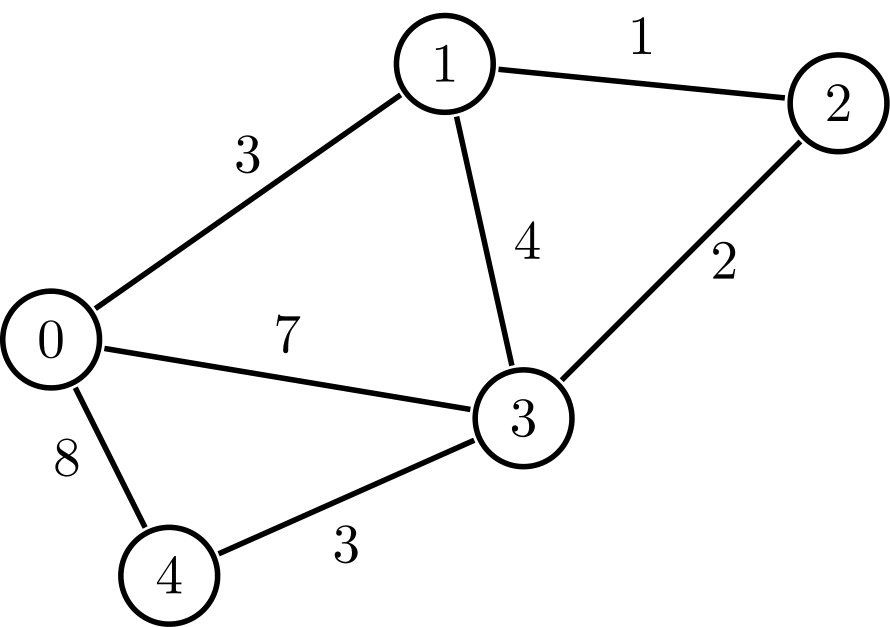
Directed Graph
Weighted Graph
Graph ADT
Core operations:
- Creating
- Destroying
- Inserting vertex/edge
- Deleting vertex/edge
- Searching for vertex /edge
We will assume simplicity that vertexes are ints.
Graph ADT
#include <stdbool.h>
typedef struct GraphRep *Graph;
typedef int Vertex;
typedef struct Edge {
Vertex v;
Vertex w;
} Edge;
Graph GraphNew(int);
void GraphEdgeInsert(Graph, Edge);
void GraphEdgeRemove(Graph, Edge);
bool GraphAdjacent(Graph, Vertex, Vertex);
void GraphShow(Graph);
void GraphDestroy(Graph);
Graph.h
Feedback

COMP2521 21T2 - 5.1 - Graph ADT
By haydensmith
COMP2521 21T2 - 5.1 - Graph ADT
- 1,413



