COMP2521
Data Structures & Algorithms
Week 5.3
Graph Traversal
Author: Hayden Smith 2021
In this lecture
Why?
- Graphs aren't very useful if all we're doing is storing things in them. We need to effectively search and traverse them to gather information
What?
- Traverse and searching a graph
- Breadth-first-search
- Depth-first-search
Why do we use graphs?
Allow us to ask these kinds of questions:
- Can we remove an edge and keep the graph connected?
- Is a vertex reachable starting from somewhere else?
- What is the quickest way to get from one node to another?
- Is there a tree that links all vertices?
Why do we use graphs?
There are 3 topics we will focus on relating to traversal. All rely on very similar algorithms and processes, they're just used to different extents.
Traverse for Item Searching
Using an algorithm to move between nodes to look for a value
Traverse for Path Finding
Using an algorithm to look for a value, but keep track of how to get there
Traverse Fully
Like path finding, except we're just exploring the entire graph, not looking for specific value
Graph Traversal (/Search)
Graph Traversal is the systematic exploration of a graph via the edges. The focus is often between exploring paths between a starting vertex and a finish vertex.
- Solutions can be iterative or recursive
- Sometimes need to store the path we explore as we explore it, and sometimes store a list of nodes we've visited
Graph Traversal
There are two primary methods we'll be using to traverse a graph:
- Depth-first search (go deep)
- Iterative & recursive solutions
- Breadth-first search (go wide)
- Iterative solutions
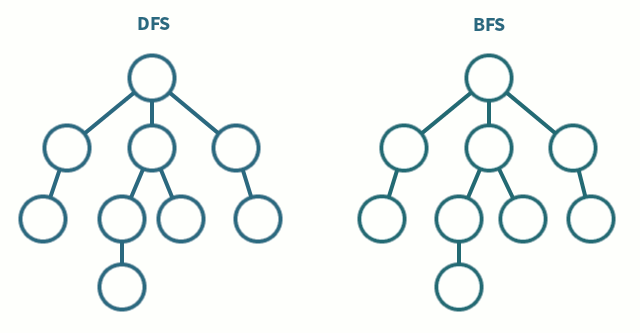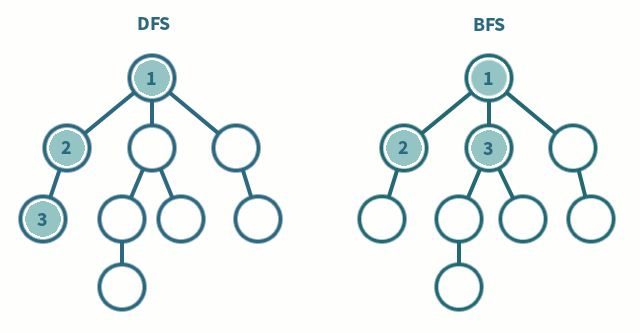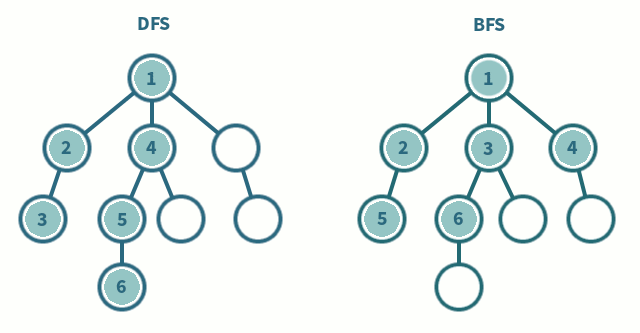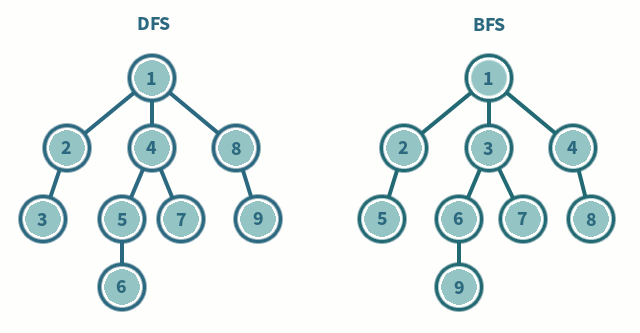
Graph Traversal
Both approaches ignore some edges by remembering previously visited vertices (this also prevents cycles)
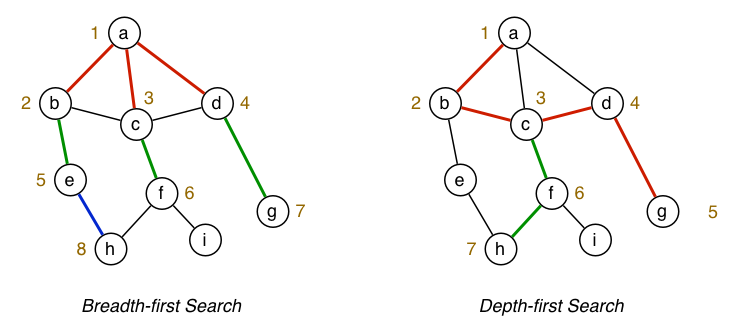
Breadth First Search
Traversing with BFS is about start at a node, and expanding out equally from there. You visit all the neighbours of the current vertex, then you visit all the neighbours of those neighbours. Etc.
BFS - Example Path Find
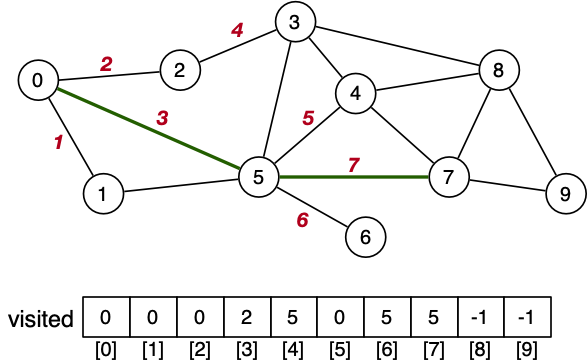
BFS - Algorithm
A very tricky algorithm to describe recursively. Typically we do it iteratively
findPathBFS(G,src,dest):
visited[] // store previously visited node
for all vertices v∈G:
visited[v]=-1
found = false
visited[src] = src
enqueue src into queue Q
while not found ∧ Q is not empty:
dequeue v from Q
if v = dest:
found = true
else:
for each (v,w) ∈ edges(G) with visited[w] = -1:
visited[w] = v
enqueue w into Q
end while
if found:
display path in dest..src order
BFS - Cost Analysis
For an adjacency list representation:
Each vertex visited at most once. Cost => O(V)
Visit all edges incident on visited vertices. Cost => O(E)
BFS: O(V + E) (adjacency list)
Depth First Search
Traversing with DFS is about going as deep as possible until you reach a dead end, and then unwinding back through nodes until there is another branch to take.
DFS - Algorithm
An iterative DFS is identical to an iterative BFS, except we use a stack instead of a queue.
findPathDFS(G,src,dest):
visited[] // store previously visited node
for all vertices v ∈ G:
visited[v] = -1
found = false
visited[src] = src
push src into stack S
while not found ∧ Q is not empty:
pop stack from S
if v = dest:
found = true
else:
for each (v,w) ∈ edges(G) with visited[w] = -1:
visited[w] = v
push w into stack S
end while
if found:
display path in dest..src order
DFS - Recursive
Recursive solutions are a bit more elegant.
Full Traversal
Path Checking
visited = {}
depthFirst(G,v):
visited = visited ∪ {v}
for all (v,w) ∈ edges(G):
if w ∉ visited:
depthFirst(G,w)
visited = {}
hasPath(G,src,dest):
return dfsPathCheck(G,src,dest)
dfsPathCheck(G,v,dest):
visited = visited ∪ {v}
for all (v,w) ∈ edges(G):
if w = dest: // found edge to dest
return true
else if w ∉ visited:
if dfsPathCheck(G,w,dest):
return true // found path via w to dest
return false // no path from v to destPath Finding
visited[] // store previously visited node
findPath(G,src,dest):
for all vertices v ∈ G:
visited[v] = -1
visited[src] = src // starting node of the path
if dfsPathCheck(G,src,dest):
// show path in dest..src order
v = dest
while v ≠ src:
print v"-"
v = visited[v]
print src
dfsPathCheck(G,v,dest):
for all (v,w) ∈ edges(G):
if visited[w] = -1:
visited[w] = v
if w = dest: // found edge from v to dest
return true
else if dfsPathCheck(G,w,dest):
return true // found path via w to dest
return false // no path from v to destDFS - Recursive Path Find
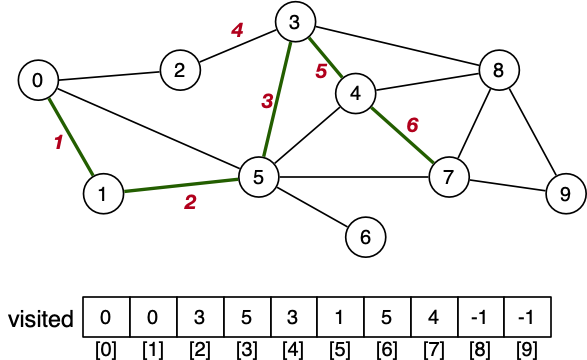
DFS - Cost Analysis
For an adjacency list representation:
Each vertex visited at most once. Cost => O(V)
Visit all edges incident on visited vertices. Cost => O(E)
BFS: O(V + E) (adjacency list)
DFS - Other
DFS does not guarantee optimal solution
Example below clearly does not find shortest path
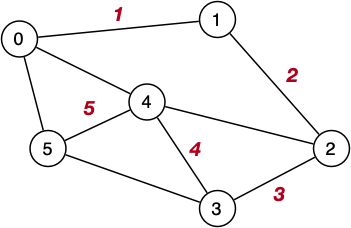
Full Traversal
A full traversal of a tree is essentially using BFS or DFS to find a spanning tree
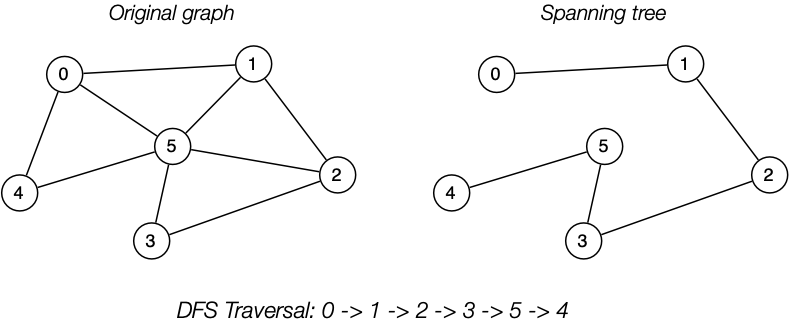
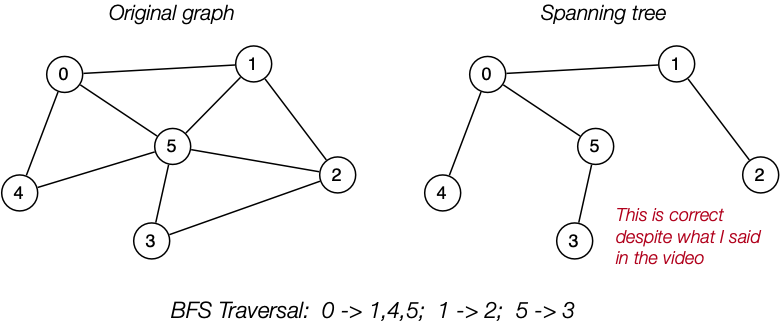
Feedback

COMP2521 21T2 - 5.3 - Graph Traversal
By haydensmith
COMP2521 21T2 - 5.3 - Graph Traversal
- 2,278



