COMP2521
Data Structures & Algorithms
Week 5.4
Graph Algorithms
Author: Hayden Smith 2021
In this lecture
Why?
- There are a range of further algorithms that can be used to explore graphs
What?
- Cycle Checking
- Connected Components
- Hamiltonian Path and Circuit
- Euler Path and Circuit
Cycle Checking
A graph has a cycle if, at any point in the graph:
- It has a path of length > 2,
- Where start vertex = end vertex, and
- Without using any edge more than once
Cycle Checking
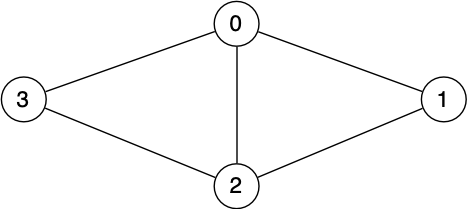
This graph has 3 distinct cycles: 0-1-2-0, 2-3-0-2, 0-1-2-3-0
Cycle Checking
This graph has MANY cycles: 0-4-3-0, 2-4-5-2, 0-1-2-5-4-6-3-0, etc...
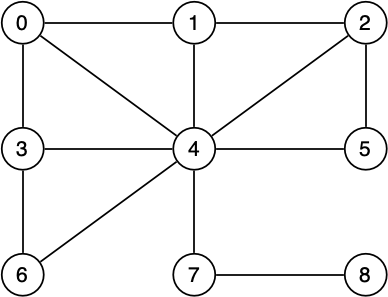
Cycle Checking
Cycle checking involves two stages: The actual checking a cycle between two vertices, and the looping over all possible vertex combinations.
Implementation in C:
Vertex *visited;
bool hasCycle(Graph g, Vertex s) {
bool result = false;
visited = calloc(g->nV,sizeof(int));
for (int v = 0; v < g->nV; v++) {
for (int i = 0; i < g->nV; i++)
visited[i] = -1;
if (dfsCycleCheck(g, v, v)) {
result = true;
break;
}
}
free(visited);
return result;
}
bool dfsCycleCheck(Graph g, Vertex v, Vertex u) {
visited[v] = true;
for (Vertex w = 0; w < g->nV; w++) {
if (adjacent(g, v, w)) {
if (!visited[w]) {
if (dfsCycleCheck(g, w, v))
return true;
}
else if (w != u)
return true;
}
}
return false;
}
Connected Components
For a given graph (which may be disjoint), we want to find out: How many connected subgraphs are there?
Easiest solution: Create a componentOf[] array, where each index refers to a vertex, and the value at that index refers to which graph it's in.
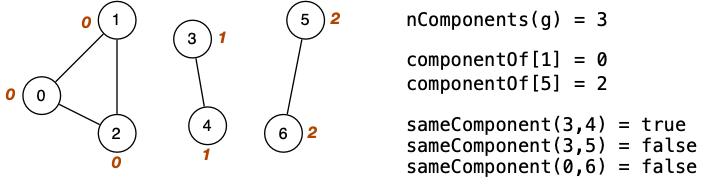
Connected Components
For a given graph (which may be disjoint), we want to find out: How many connected subgraphs are there?
Easiest solution: Create a componentOf[] array, where each index refers to a vertex, and the value at that index refers to which graph it's in.

Algorithm
components(G):
for all vertices v ∈ G:
componentOf[v] = -1
compID = 0 // component ID
for all vertices v ∈ G:
if componentOf[v] == -1:
dfsComponent(G, v, compID)
compID = compID + 1
dfsComponent(G, v, id):
componentOf[v] = id
for each (v,w) ∈ edges(G):
if componentOf[w] == -1:
dfsComponent(G, w, id)Caching Info
For applications where connectivity is critical, we can't afford to run components() each time. But we can cache some information by adding information to our graph implementation struct. Adding or removing of edges may increase or decrease nC.
Another speedup: Ensure v, w are in the same component before starting a search
typedef struct GraphRep *Graph;
struct GraphRep {
...
int nC; // # connected components
int *cc; // which component each vertex is contained in
... // i.e. array [0..nV-1] of 0..nC-1
}Hamiltonian Path & Circuit
Hamiltonian path problem: A path connecting two vertices (v, w) in graph G such that the path includes each vertex exactly once.
Hamiltonian Circuit: A Hamiltonian path where the starting vertex = ending vertex
Real world applications include:
- Traveling Salesman
- Bus routes
Hamiltonian Path Examples

Hamiltonian Path Search
Approach:
- Generate all possible simple paths (e.g. using DFS)
- Keep a counter of vertices visited in current path
- Stop when find a path containing V vertices
Expressed via a recursive DFS algorithm. Very similar to path finding, except we track path lengths.
Algorithm
hasHamiltonianPath(G,src,dest):
visited[] // keep track of visited vertices
for all vertices v ∈ G:
visited[v] = false
return hamiltonR(G, src, dest, #vertices(G) - 1)
hamiltonR(G,v,dest,d):
if v = dest:
return d == 0
else:
visited[v] = true
for each (v,w) ∈ edges(G) where not visited[w]:
if hamiltonR(G, w, dest, d - 1):
return true
visited[v] = false // reset visited mark
return falseAnalysis
Worst case: O((V - 1)!)
- As there are (V-1)! paths to be examined - as we have to consider every possible path.
- There is no known simpler algorithm for this task, which makes it NP-hard.
Euler Path & Circuit
Euler path problem: Find a path connecting two vertices (v, w) in graph G such that the path includes each edge exactly once.
Euler Circuit: A Euler path where the starting vertex = ending vertex
Real world applications include:
- Post delivery
- Garbage truck pickup
Euler Path & Circuit
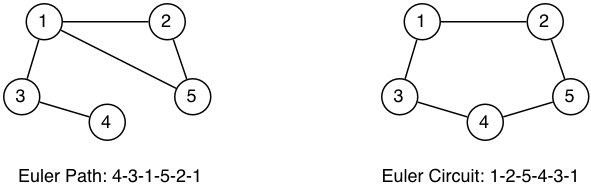
Origins
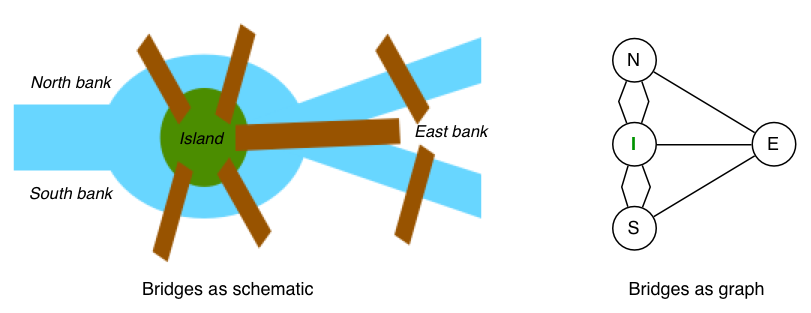
Origins are from Leonhard Euler who was trying to find a way to cross all the bridges of Konigsberg exactly once on a walk through the town.
Finding a Euler path/circuit
A brute force (do many checks, would be O(n!)) would be to find every possible path and check if it's a Euler path. But we have a shortcut:
1. A graph has a Euler circuit if and only if it is connected and all vertices have even degree
2. A graph has a Euler path (non-circuit) if and only if it is connected and exactly two vertices had odd degree
Algorithm: Euler path/circuit
hasEulerPath(G, src, dest):
if src != dest:
if degree(G, src) is even and degree(G,dest) is even:
return false
for all vertices v ∈ G:
if v != src and v != dest and degree(G,v) is odd:
return false
return trueIf we assume connectivity is already checked:
- O(V) if degree is O(1) lookup
- Just a loop through all vertices
- O(V^2) if degree needs to be calculated
- To find degree need to look through V vertexes
Feedback

COMP2521 21T2 - 5.4 - Graph Algorithms
By haydensmith
COMP2521 21T2 - 5.4 - Graph Algorithms
- 1,490



