COMP2521
Data Structures & Algorithms
Week 7.2
Directed & Weighted Graphs
Author: Hayden Smith 2021
In this lecture
Why?
- In the real world graph, edges often have a sense of direction, and also a sense of cost to traverse.
What?
- Directed Graphs
- Weighted graphs
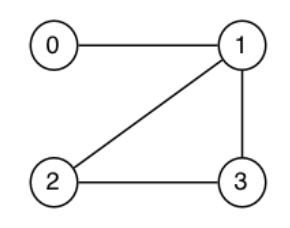
A more common graph
Often, graphs don't look like the one on the left. They look like the one on the right. They have directions and weights.
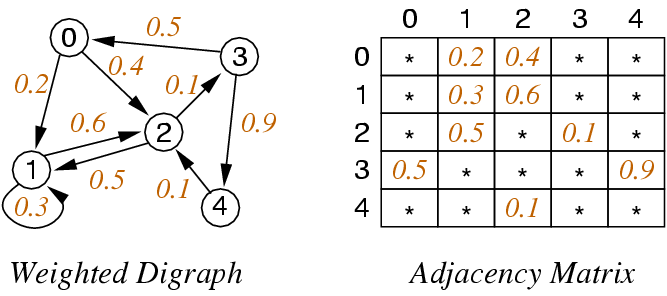
Directed graphs (Digraphs)
Digraphs are very similar to normal graphs, except that edges have a sense of direction such that:
v → w ≠ w → v
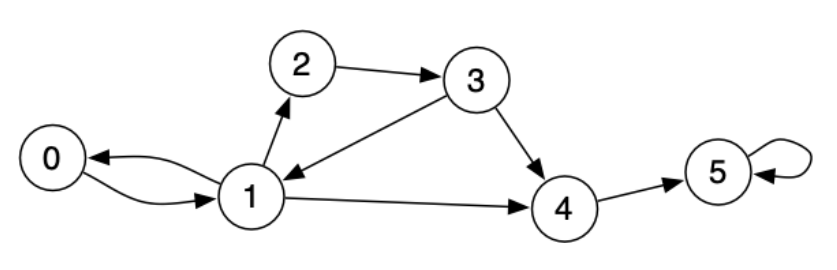
Digraph Properties
- Directed path, directed cycle, as you expect
-
Degree of a vertex:
- Outdegree: deg(v) = number of edges of the form (v, _)
- Indegree: deg^-1(v) = number of edges of the form (_, v)
- Reachability: w is reachable from v if there is directed path v,…,w
- Strong connectivity: every vertex is reachable from every other vertex
- Directed acyclic graph: contains no directed cycles
Digraph Implementations
- Virtually the same as undirected graphs, except the edge pairs have a sense of direction
| Array of edges | Adjacency Matrix | Adjacency List | |
|---|---|---|---|
| Space usage | E | V^2 | V + E |
| Insert edge | E | 1 | deg(v) |
| exists edge (v,w) | E | 1 | deg(v) |
| get edges leaving v | E | V | deg(v) |
Digraph Implementations
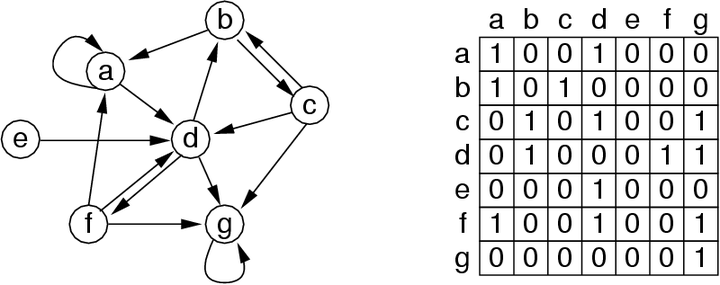
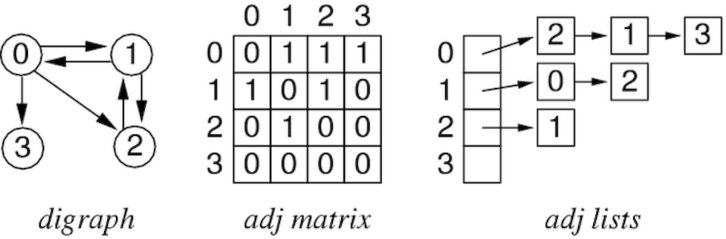
Traversing
Identical to undirected graphs
Weighted Graphs
Weighted graphs are similar to our previous graphs, except the edges have a sense of COST / WEIGHT.
Generally speaking, this means that when we traverse the graph certain edges will be "cheaper" to explore than others.
Each edge is now (s, t, w) instead of (s, t)
Weighted Graphs
Weighted graphs have substantially more parallels to reality:
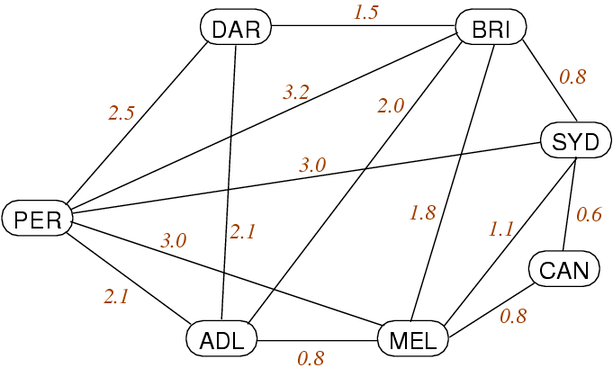
Weighted Graphs
There are two main problems we try to solve with weighted graphs:
1. Cheapest way to connect all vertices (minimal spanning tree problem) - for undirected weighted graphs
2. Cheapest way to get from A to B (shortest path problem) - for directed weighted graphs
We will cover these in more detail.
Weighted Graphs
Adjacency Matrix Representation
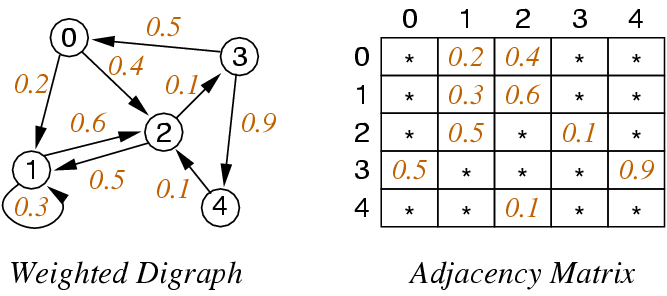
Weighted Graphs
Adjacency List Representation
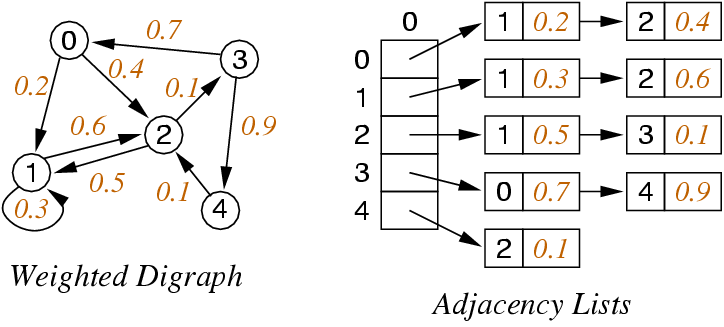
Weighted Graphs
Array/List of Edges Representation
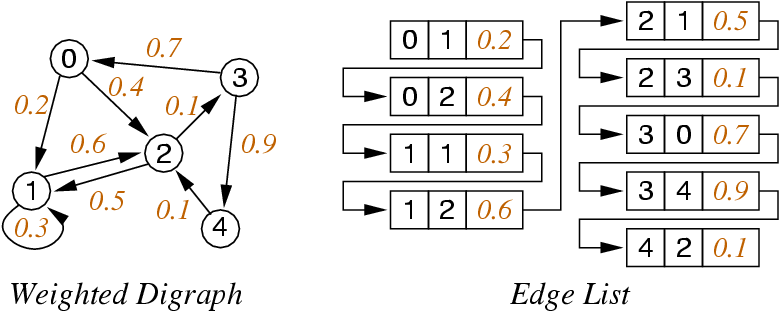
Key changes to ADT/implementation
Graph.h
// edges are pairs of vertices (end-points) plus weight
typedef struct Edge {
Vertex v;
Vertex w;
int weight;
} Edge;
// returns weight, or 0 if vertices not adjacent
int GraphAdjacent(Graph, Vertex, Vertex);typedef struct GraphRep {
int **edges; // adjacency matrix storing weights
// 0 if nodes not adjacent
int nV; // #vertices
int nE; // #edges
} GraphRep;
int GraphAdjacent(Graph g, Vertex v, Vertex w) {
assert(valid graph, valid vertices)
return (g->edges[v][w] != 0);
}
void GraphEdgeInsert(Graph g, Edge e) {
assert(valid graph, valid edge)
// edge e not already in graph
if (g->edges[e.v][e.w] == 0) g->nE++;
// may change weight of existing edge
g->edges[e.v][e.w] = e.weight;
g->edges[e.w][e.v] = e.weight;
}
void GraphEdgeRemove(Graph g, Edge e) {
assert(valid graph, valid edge)
// edge e not in graph
if (g->edges[e.v][e.w] == 0) return;
g->edges[e.v][e.w] = 0;
g->edges[e.w][e.v] = 0;
g->nE--;
}Graph.c
Feedback

COMP2521 21T2 - 7.2 - Weighted/Directed Graphs
By haydensmith
COMP2521 21T2 - 7.2 - Weighted/Directed Graphs
- 1,164



