COMP2521
Data Structures & Algorithms
Week 9.3
Tries
Author: Hayden Smith 2021
In this lecture
Why?
- Storing a large set of strings naively can be costly, we need a more efficient way
What?
- Tries
- Tries insert
- Tries lookup
Tries
Tries are a data structure for representing strings that support O(L) lookup and insertion (where L is the length of a string)
Tries Concenptualised
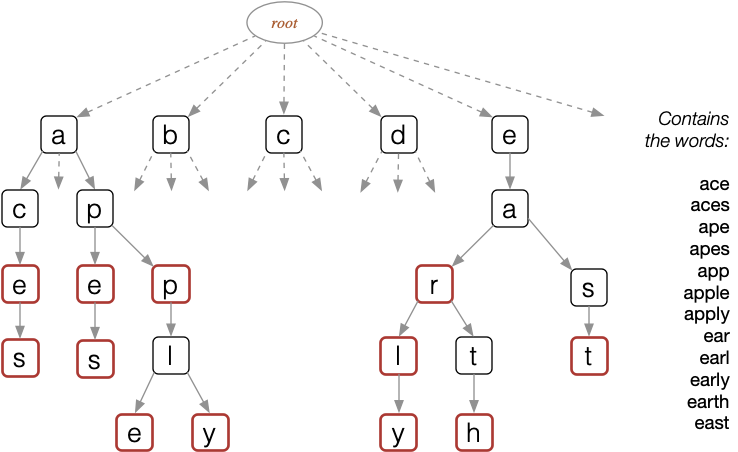
Depth of trie = length of longest word
Tries Concenptualised
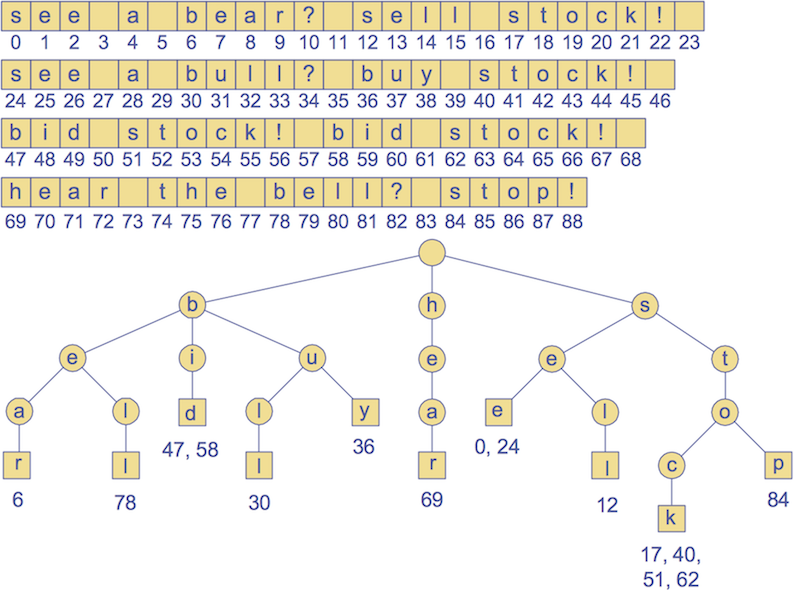
Note: Not every word here is included in the trie
Tries Structure
Each node in a trie:
- Contains one part of a key (typically one character)
- May have up to 26 children
- May be tagged as a "finishing" node
- But even "finishing" nodes may have children
- May contain other data for application (e.g. word frequency)
- A "finishing" node marks the end of one key
#define ALPHABET_SIZE 26
typedef struct Node *Trie;
typedef struct Node {
char onechar; // current char in key
Trie child[ALPHABET_SIZE];
bool finish; // last char in key?
Item data; // no Item if !finish
} Node;
typedef char *Key; // just lower-case lettersTries Search
find(trie,key):
| Input trie, key
| Output pointer to element in trie if key found
| NULL otherwise
|
| node=trie
| for each char c in key do
| | if node.child[c] exists then
| | node=node.child[c] // move down one level
| | else
| | return NULL
| | end if
| end for
| if node.finish then // "finishing" node reached?
| return node
| else
| return NULL
| end if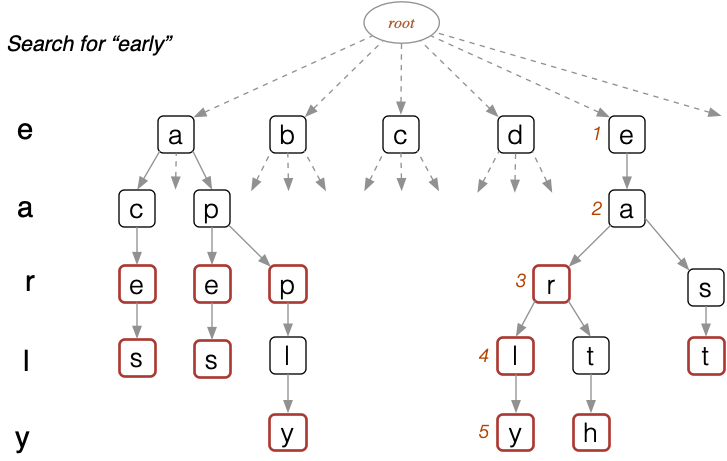
Tries Insertion
Trie insert(trie, item, key):
if trie is empty then:
t = new trie node
if m = 0 then // end of key
t.finish = true
t.data = item
else:
first = key[0]
rest = key[1..m-1]
t.child[first] = insert(t.child[first], item, rest)
return tTries Complexity
- Space complexity: O(n)
- n = Sum of lengths of all strings
- Insertion complexity: O(m)
- m = length of the key string
- Search complexity: O(m)
BST-like Tries
Above representation is space inefficient
- Each node has 26 possible children
- Even with very many keys, most child links are unused
And if we allowed all ascii chars in alphabet, 128 children
We could reduce branching factor by reducing "alphabet"
- Break each 8-bit char into two 4-bit "nybbles"
- Branching factor is 16, even for full ascii char set
- But each branch is twice as long
BST-like Tries
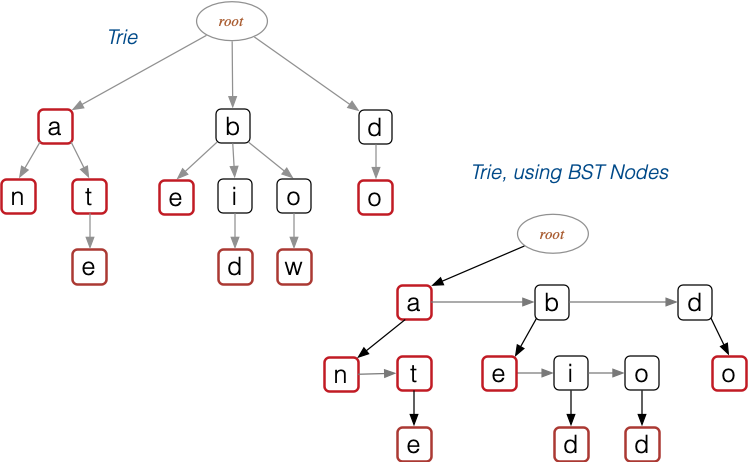
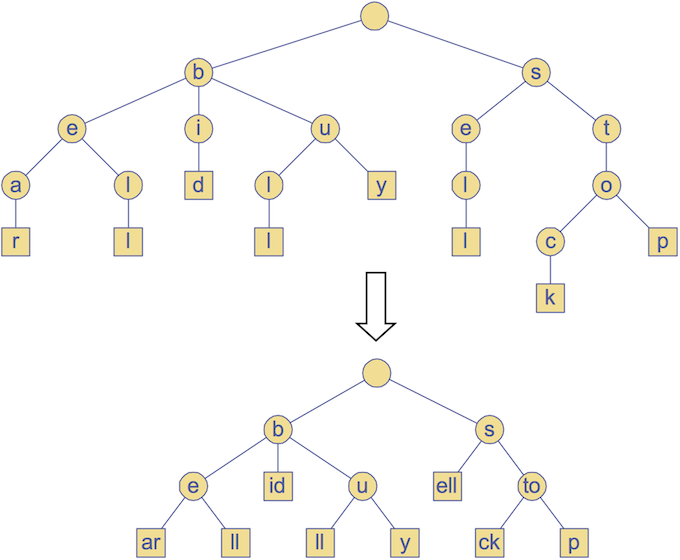
Compressed Tries
- Have internal nodes of degree ≥ 2; each node contains ≥ 1 char
- Obtained by compressing non-branching chains of nodes
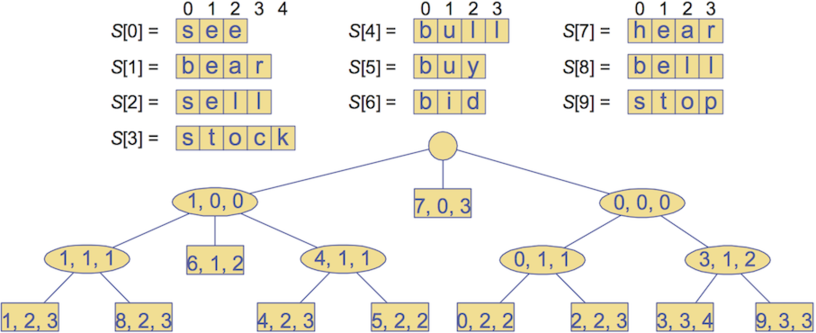
- Compact representation of compressed trie to encode array S of strings:
- Requires O(s) space (s = #strings in array S)
Compressed Tries
Feedback

COMP2521 21T2 - 9.3 - Tries
By haydensmith
COMP2521 21T2 - 9.3 - Tries
- 1,841



