RATE meeting
June 1st
Previous meeting
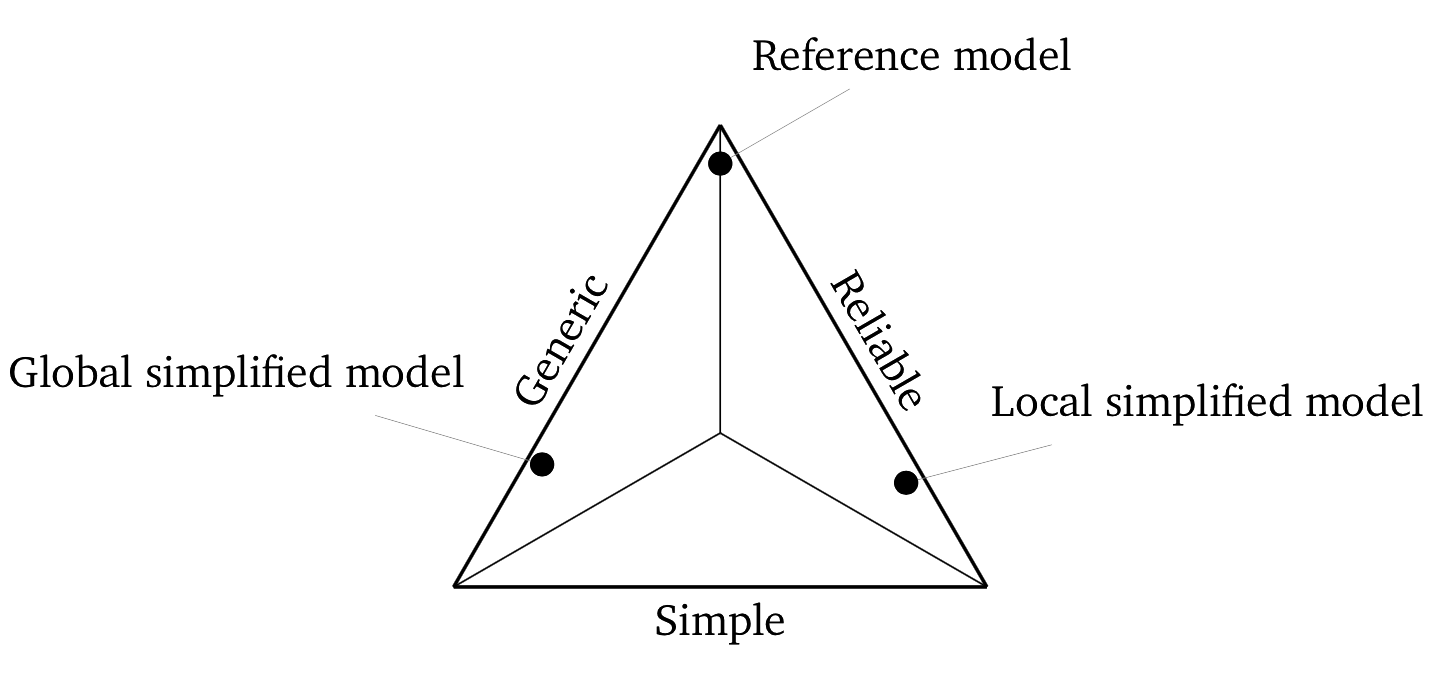
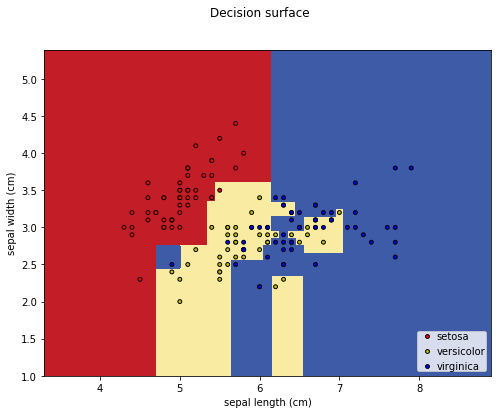
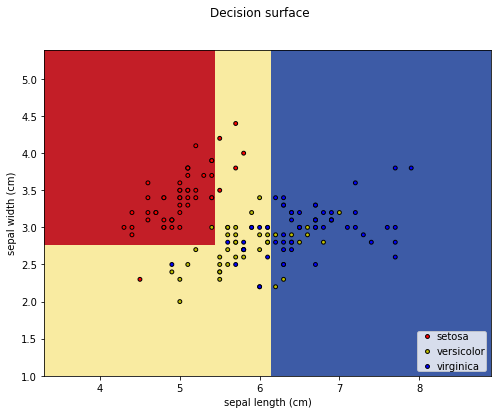
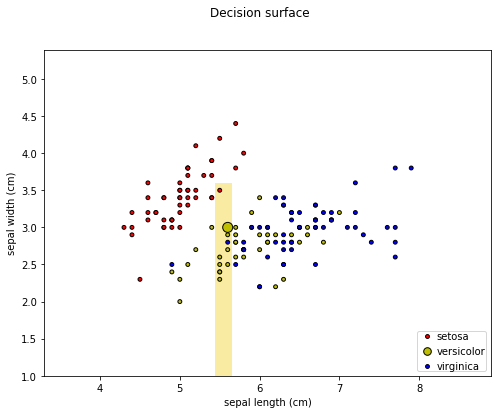
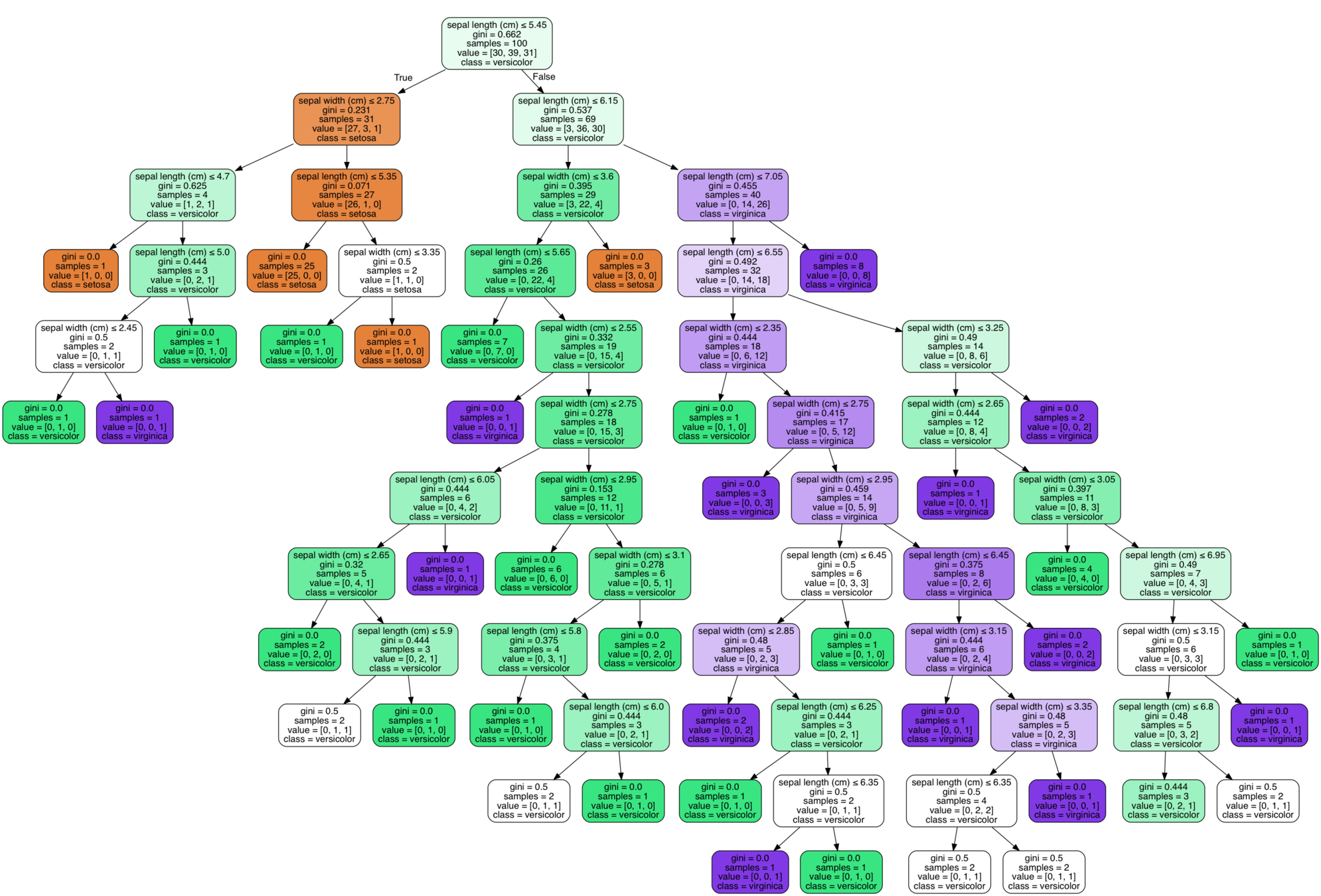
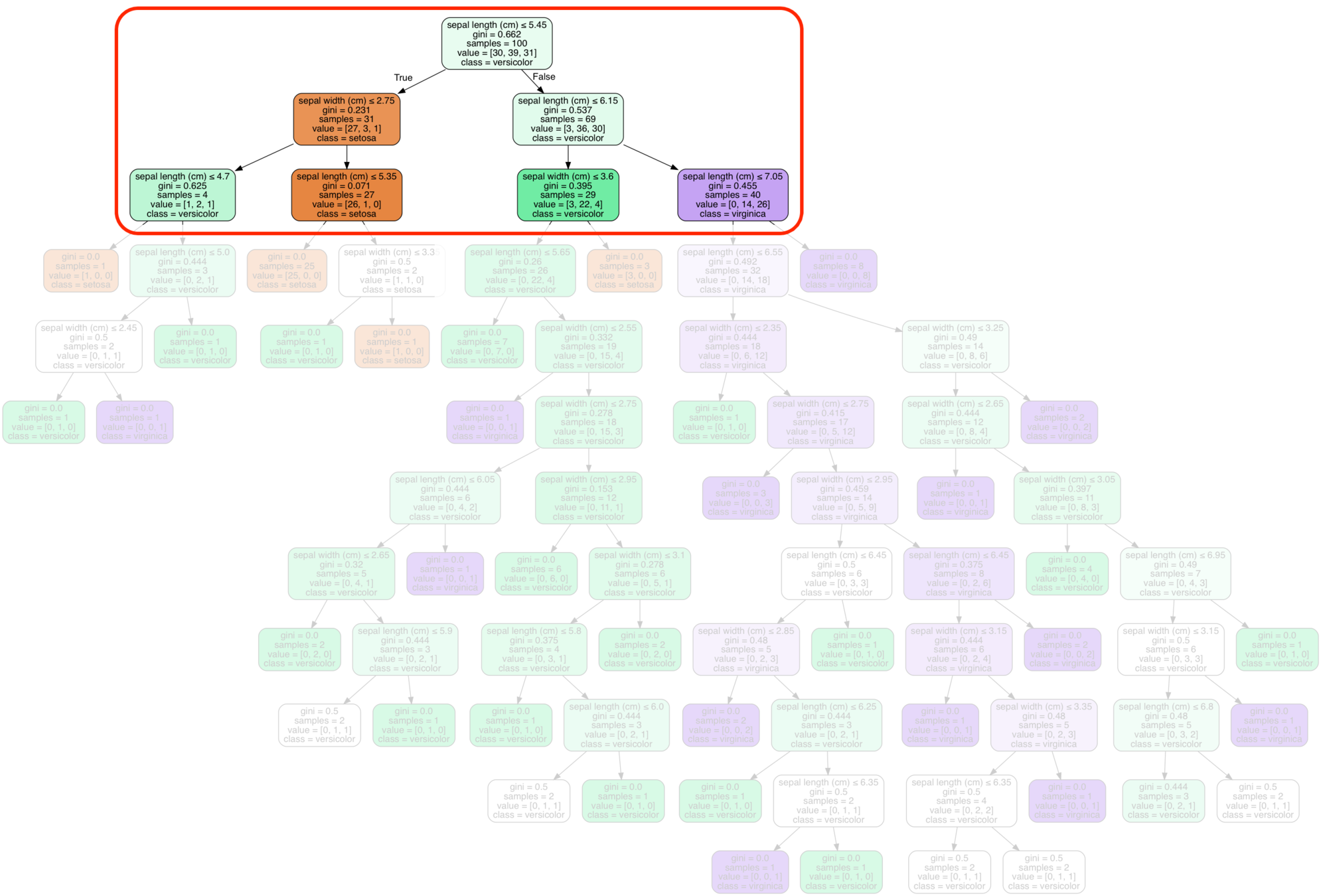
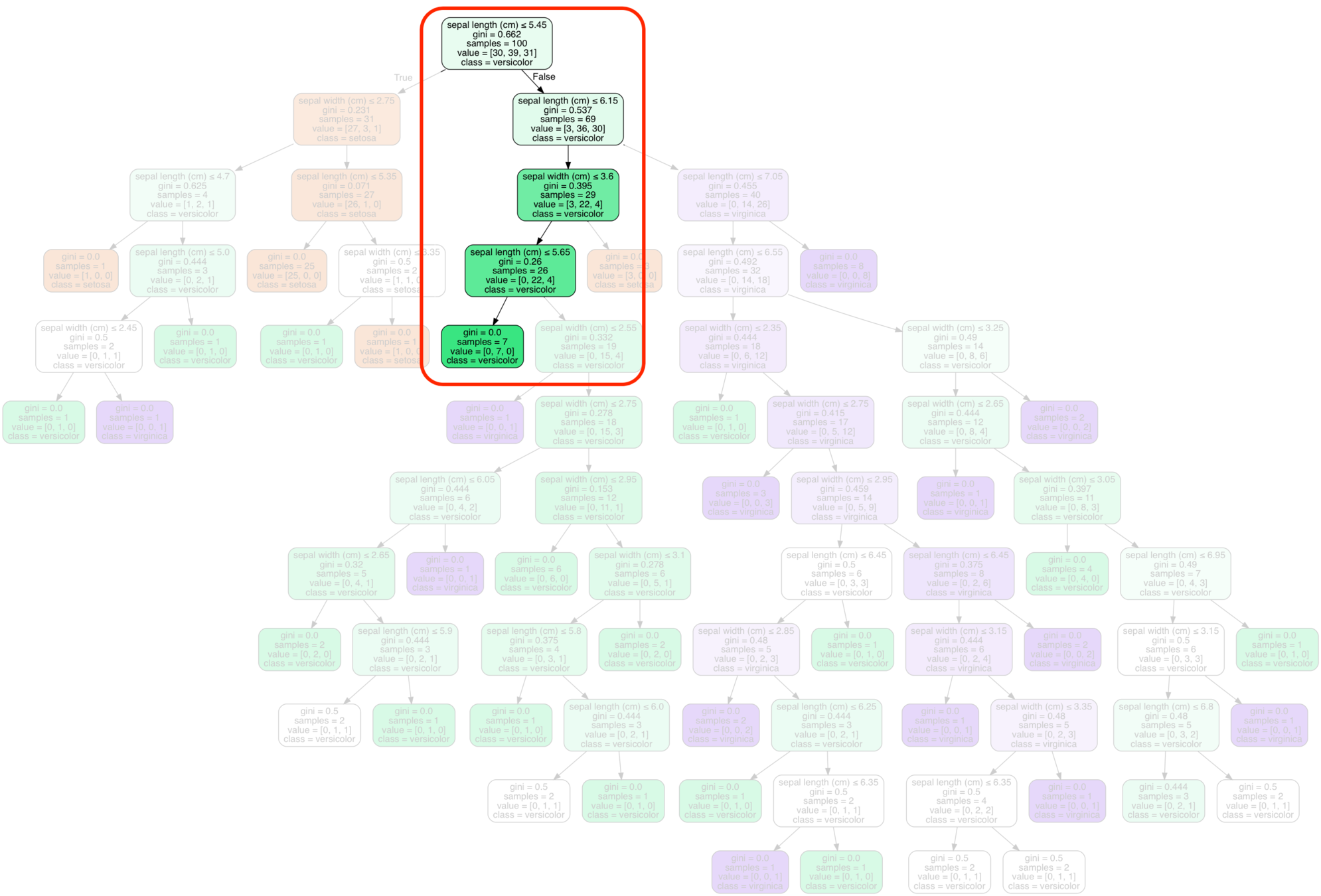
Next steps...
- Explore sub categories of high-level desiderata
(+ relations)
- Quantifiable metrics to approximate these desiderata.
Overview
Question: how to formally define an explanation?
- Philosophical models
- Formalization
- Problems:
- How do we define causality?
- what criticism of philosophical models applies to ML explanations?
Philosophical models
-
Deductive-Nomological model (Hempel, 1948)
- \(S_C\)
- The infant’s cells have three copies of chromosome 21.
- \(S_L\)
- Any infant whose cells have three copies of chromosome 21 has Down’s Syndrome.
- Y
- The infant has Down’s Syndrome.
-
Inductive-Statistical model (Hempel, 1965)
- \(S_C\)
- The man’s brain was deprived of oxygen for five con-tinuous minutes.
- \(S_L\)
- Almost anyone whose brain is deprived of oxygen for five continuous minutes will sustain brain damage.
- Y
- The man has brain damage.
-
Statistical-Relevance model (Salmon, 1979)
Any relevant contribution to Y should be considered.
Formalization
A black box model \( b: \mathcal{X}^n \rightarrow \mathcal{Y} \) maps feature space to target space.
A Machine Learning explanation \(E\) is an answer to the question:
Why are (instances of) \(\mathcal{X}_E\) classified as \(y\)?
where \(\mathcal{X}_E \subseteq \mathcal{X}\) and \(y \in \mathcal{Y}\).
Global: \( \mathcal{X}_{E} = \mathcal{X} \)
Local: \( \mathcal{X}_{E} \subset \mathcal{X} \)
Explanation contain statements \(S \in E\) that are either initial conditions \(S_C\) or statistical generalisations \(S_L\) (like IS model)
Initial conditions \(S_C\) are constraints on feature space, constituting \(\mathcal{X}_E\)
"Causality"?
Laws \(S_L\) are constraints where \(P(y)\ |\ \mathcal{X}_L) > P(y\ |\ \mathcal{X}) \) (like SR model)
\(\mathcal{X}_E \subseteq \mathcal{X}_L\)?
\(\mathcal{X}_E \cap \mathcal{X}_L \neq \emptyset\)?
Problem: Causality
Consider these various assertions about the statement:
X caused Y:
- X is a necessary and/or sufficient condition of Y.
- If X had not occurred, Y would not have occurred.
- The conditional probability of Y given X is different from the absolute probability of Y: \(P(Y\ |\ X) \neq P(Y)\).
- X appears with a non-zero coefficient in a regression equation predicting the value of Y.
- There is a causal mechanism leading from the occurrence of X to the occurrence of Y.
Problem: Causality
Ice cream consumption correlates with sun burns
Explanation
Prediction
Machine Learning explanations only capture the cause for the prediction, not the real world effect!
white box: only obtain statistical laws from the decisions made by the model.
black box: approach decision boundary such that decisions not made in the model cannot appear in explanation.
Fundamental Problem of Causal Inference
We can never observe the event and counterfactual event, hence causality can only be inferred.
With inference comes uncertainty.
However, Machine Learning prediction is deterministic, which ensures we can replay and observe what happens if the statement was not true.
- Effect should follow logically from the statements.
- Statements should contain general laws.
- Statements must be testable.
- Statements must be true.
Hempel's Conditions of Adequacy
Problem: Contradicting laws (Coffa)
- \(S_C\)
- Jones is from Texas.
- \(S_C\)
- Jones is a philosopher.
- \(S_L\)
- \(P(Millionaire\ |\ Texas) \approx 0.9\)
- \(S_L\)
- \(P(\neg Millionaire\ |\ Philosopher) \approx 0.9\)
- Y
- Jones is a millionaire and not a millionaire
Explanation / Counterexplanation
We could have a very weak explanation and a very strong counterexplanation, but just showing the explanation will not reveil this..
Reference class problem
P(Pregnancy\ |\ T.Male.Takes\ birth\ control\ pills)
= P(Pregnancy\ |\ T.Male)
= 0
P(Pregnancy\ |\ T.Female.Takes\ birth\ control\ pills)
\neq P(Pregnancy\ |\ T.Female)
- \(S_C\)
- Person is a male.
- \(S_C\)
- Person took birth control pills.
- \(S_L\)
- \(P(Pregnant\ |\ Takes\ birth\ control\ pills) > P(Pregnant)\)
- Y
- The man did not get pregnant
Salmon: maximum homogeneous reference class:
No partitions of the explanation space exist in which \(P(y\ |\ \mathcal{X}_{1})\) is significantly different from \(P(y\ |\ \mathcal{X}_{2})\)
Problem: epistemic ambiguity
Hempel: explanation is true as far as the knowledge of the explainer goes.
- \(S_C\)
- Jones is infected.
- \(S_C\)
- Jones is administered penicillin.
- \(S_L\)
- \(P(Recovery\ |\ Infected.Penicillin) \approx 0.9\)
- Y
- Jones recovers
- \(S_C\)
- Jones is infected.
- \(S_C\)
- Jones is administered penicillin.
- \(S_C\)
- Jones does not respond well to penicillin.
- \(S_L\)
- \(P(\neg Recovery\ |\ Infected.Penicillin.NotRespondWell) \approx 0.9\)
- Y
- Jones will not recover
Deck June 1st
By iamdecode
