CTF-Crypto

CRYPTOLOGY

by watermelon

who am i?

西瓜

建電副社+學術
揪寒訓
APCS忘記帶身分證的傻逼
I人不敢跟你打招呼一定是因為我社恐
什麼都學啥都學不好
夜貓子
:suicide:
貓戰/LOL 玩家

推個研究大攝影

Index

intro

Problems

Practice

這頁真是做的可有可無

這句也是

Crypto-intro

{Crypto}

Crypto 密碼學(cryptology)
網路安全的基礎
經常用到的能力
- python
  - 許多現成的工具模組不用像C++手刻(浪費時間)
  - 語法簡單不難學
- 數學-數論
  - 大概了解加密演算法的原理就好

真正的Crypto高手只要一張紙一支筆以及Python環境就可以稱霸全場了

{Crypto}

分類
- 編碼
- 古典密碼學
- 現代密碼學

{Crypto}

分類
- 編碼、古典密碼學
  - 密碼學的基本功
  - 大多變化較少比較死
  - 遇到題目基本上就套code就好
  - 非常好工具：CyberChef
- 現代密碼學
  - 偏難、能講多少講多少

{Encode}

編碼

{Encode}

編碼
內容單純
一般被認為無安全性
定義
- 用f(x)加密
- 用f⁻¹(x)解密
種類五花八門，不用全會
- 有基礎認識
- google~~GPT~~能力

{Encode}

明文(plaintext)

kea is so dian

編碼(encoded data)

a2VhIGlzIHNvIGRpYW4=

f(x)

f⁻¹(x)

{反函數}

可以簡單理解為輸入輸出交換
兩個變數就交換就好
只是剛好高二對數會講
- f(x) = logₐx ,則
- f⁻¹(x) = aˣ

有超連結可以點

{Morse Code}

摩斯密碼
發明目的是通訊
長度與字元出現的頻率成反比
Decode：
- CyberChef：前面講過了
- Morse-Sound-Receiver
  - 處理音檔摩斯密碼

{Hex}

十六進制
把數字/英文ascii碼轉成16進位
前綴為"0x"
用途：
- 色碼 (ex:#FFFFFF黑色)
- 記憶體位置
- 機器指令(ex:x86)
- 文件原始內容(misc)
工具：
- CyberChef
- Hex.it

進制	英文	範圍	前缀
二進制	Binary	0-1	0b
八進制	Octal	0-7	0
十進制	Decimal	0-9	\
十六進制	Hexadecimal	0-9, A-F	0x

{carry system}

Dec(十進位)

\setminus 5678 \ or \ 5678_{10} \newline = 8\times 10^{\color{Red} 0} + 7\times 10^{\color{Red}1}+ 6\times 10^{\color{Red}2}+ 5\times 10^{\color{Red}3}

{carry system}

Hex(十六進位)

\mathsf{0xabc} \ or \ \mathsf{abc_{16}} \newline = c\times 16^{\color{Red} 0} + b\times 16^{\color{Red}1}+ c\times 16^{\color{Red}2} \newline = 12\times 16^{\color{Red} 0} + 11\times 16^{\color{Red}1}+ 10\times 16^{\color{Red}2} \newline = 2748

{Hex->Dec}

轉換方法
- CyberChef
- Python

# 不一定要有前後綴
hex_value = "0xabc"
# int(x,base=10) 
# x:字串或者數字 base: 進制數 預設為10
dec_val = int(hex_value,16)
# 輸出
print(dec_val) # 2748

{Dec->Hex}

轉換方法
- CyberChef
- Python

# 不一定要有前後綴
dec_value = "2486"
# hex(x) x:十進位數字
hex_val = hex(dec_value)
# 輸出
print(dec_val) #0x9b6

{Hex->Str}

轉換方法
- CyberChef
- Python

hex_data = "686578"  # 16 進位字串
# 數據的長度是奇數 需補0
decoded_string = bytes.fromhex(hex_data).decode("utf-8")
print(decoded_string)  # 輸出：'hex'

# 自動補零版
def num2str(num):
    # 去掉 '0x' 和可能存在的 'L'
    hex_str = hex(num)[2:].replace("L", "")  
    if len(hex_str) % 2 == 1:
        hex_str = "0" + hex_str  # 補零
    return bytes.fromhex(hex_str).decode("utf-8")

{Urlencode}

瀏覽器跟網站傳送資料時解決特殊字符
每個code都是"%xx" (ex:%20 就是 " ")
把有中文的網址複製貼到其他地方
decode:
- CyberChef
- 直接丟到瀏覽器去查(google.com/search?q=<code>)
範例：%E5%BB%BA%E5%8C%97%E9%9B%BB%E8%B3%87
試試看：
- %E6%89%80%E4%BB%A5%E4%BD%A0%E8%A6%81%E5%A0%B1%E5%AF%92%E8%A8%93
- %E7%BE%85%E5%82%91%E8%AA%AA%E4%BD%A0%E6%98%AF2486

{BrainFuck}

腦幹
極小化的程式語言難以閱讀
圖靈完備

{BrainFuck}

腦幹
極小化的程式語言難以閱讀
圖靈完備

{BrainFuck}

腦幹
工具：
- Cyberchef

{BrainFuck}

腦幹
工具：
- ~~Cyberchef~~
- https://www.cachesleuth.com/bfook.html
酷東西
- +[------->++<]>.---------.[--->+<]>-.+[->+++<]>.+++++++++++++.[-->+++++<]>+++.++[->+++<]>+.++++++++.-..-------------.-[->+++<]>.++[->+++<]>+.++.[->++++++<]>.+[->+++<]>.--[--->+<]>-.---[->++++<]>+.-[---->+<]>+++.---[->++++<]>+.-----.>++++++++++.-[------->+<]>-.---------.[--->+<]>-.+[->+++<]>.+++++++++++++.[-->+++++<]>+++.++[->+++<]>+.++++++++.-..-------------.-[->+++<]>.++[--->++<]>.-------.[--->+<]>---.[---->+<]>+++..---[->++++<]>+.-[---->+<]>+++.+[->+++<]>+.+++++++++++.++++++++.---------.

{JSFuck}

~~JS幹~~

借盧卡斯太強辣

{JSFuck}

~~JS幹~~
工具：
- ~~Cyberchef~~
- encoder / decoder
- 瀏覽器的console / js
特徵：只有 "[]()!+"

{JSFuck}

~~JS幹~~
長到靠北我就不給範例了
真的在打比賽有遇過 (但是是出在reverse)
應用：
- 混淆jQuery代碼：增加被破解難度
- 缺乏JS特徵：可繞過惡意代碼檢測、XSS
類似的東西：
- aaencode：顔文字版的jsfuck
- jjencode：很多 $

jjencode

{Base-X}

以X個字元來表示二進位資料有剩餘的補"="
ascii code: 8 bit/char = 2⁸
以最常見的Base64為例： 64 = 2⁶
- [8,6] = 24 , 24/8 = 3 , 24/6 = 4
- 🉐 每3個ascii字母可以encode成4個字元
顯然用講的有點抽象：

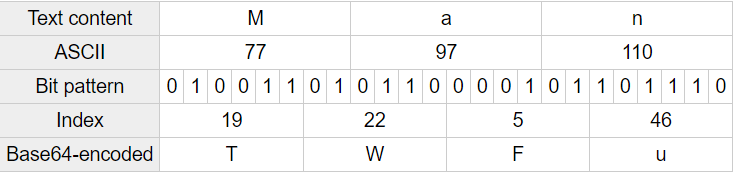
{Base-X}

以X個字元來表示二進位資料有剩餘的補"="
補 "="原則：
- 位數為3n+2：最後補上==
- 位數為3n+1：最後補上=
工具：
- CyberChef
- 自訂性高的python庫
- python內建

這個是不同進位制的轉換

import base64
raw = "melon_idoita"
data = base64.b64encode(raw) # encode
assert raw == base64.b64decode(data) # decode

{Base-X}

編碼	字符集
base64	a-z,A-Z,0-9.+,/,=
base32	A-Z,2-7,=
base16	0-9,A-F,=

hex和base16只差在字母大小寫,why?

{柯克霍夫原則}

即使密碼系統的任何細節已為人悉知，只要密匙（key，又稱金鑰或金鑰）未洩漏，它也應是安全的。

{密碼學分類}

對稱加密：大多古代密碼
- 加密者：明文密文

解密者：明文密文

同一把密鑰

{密碼學分類}

非對稱加密：大多數現代密碼
- 加密者：明文密文

解密者：名文密文

公鑰：沒有洩漏問題
只能加密不能解密

{密碼學分類}

非對稱加密：大多數現代密碼
- 加密者：明文密文

解密者：名文密文

私鑰：必須保密

只能解密

私鑰可以推導出公鑰，但公鑰推導出私鑰極度困難

(ex:計算時間好幾億年)

{密碼學分類}

非對稱加密：大多數現代密碼
- 加密者：明文密文

解密者：名文密文

私鑰：必須保密

只能解密

公鑰：沒有洩漏問題
只能加密不能解密

防止公鑰被洩漏而有資安風險

Classical cipher

古典密碼

{位移密碼}

{簡單位移密碼}

直接舉例(M=明文，K=密鑰，C=密文)
M = "melonCTF{cuz_i_am_a_chill_guy}"
K = "4213"
把字串切成len(K),把每個片段中的第i個移到第Kᵢ個
例：

C = "leomTCFnucz{_ia_a__mihlcg_ul}y"

1	2	3	4
m	e	l	o
4	2	1	3

{簡單位移密碼}

特徵：
- 明文有的字密文也有
- skill:找 "CTF" 或者 "{" 、 "}"
python code:

def shift_encode(m,k):
    c = ""
    for i in range(0, len(m), len(k)):
        m1 = [""]*len(k)
        if i+len(k) > len(m):
            temp = m[i:]
        else:
            temp = m[i:i+len(k)]
        for j in range(len(temp)):
            m1[int(k[j])-1] = temp[j]
        c += "".join(m1)
    return c

if  __name__ == '__main__':
    m = "melonCTF{cuz_i_am_a_chill_guy}"
    k = "4213"
    print (shift_encode(m,k))

{}

像是一個寬度為k的柵欄總共會有k個柵欄
python code:

def shift_encode(m,k):
    c = ""
    for i in range(0, len(m), len(k)):
        m1 = [""]*len(k)
        if i+len(k) > len(m):
            temp = m[i:]
        else:
            temp = m[i:i+len(k)]
        for j in range(len(temp)):
            m1[int(k[j])-1] = temp[j]
        c += "".join(m1)
    return c

if  __name__ == '__main__':
    m = "melonCTF{cuz_i_am_a_chill_guy}"
    k = "4213"
    print (shift_encode(m,k))

例：(k=3)

1 2 3 4 5 6 7 8 9

我自己將他命名為跳k個好了

{}

像是一個寬度為k的柵欄總共會有k個柵欄
python code:

def shift_encode(m,k):
    c = ""
    for i in range(0, len(m), len(k)):
        m1 = [""]*len(k)
        if i+len(k) > len(m):
            temp = m[i:]
        else:
            temp = m[i:i+len(k)]
        for j in range(len(temp)):
            m1[int(k[j])-1] = temp[j]
        c += "".join(m1)
    return c

if  __name__ == '__main__':
    m = "melonCTF{cuz_i_am_a_chill_guy}"
    k = "4213"
    print (shift_encode(m,k))

例：(k=3)

1 2 3 4 5 6 7 8 9

147

{}

像是一個寬度為k的柵欄總共會有k個柵欄
python code:

def shift_encode(m,k):
    c = ""
    for i in range(0, len(m), len(k)):
        m1 = [""]*len(k)
        if i+len(k) > len(m):
            temp = m[i:]
        else:
            temp = m[i:i+len(k)]
        for j in range(len(temp)):
            m1[int(k[j])-1] = temp[j]
        c += "".join(m1)
    return c

if  __name__ == '__main__':
    m = "melonCTF{cuz_i_am_a_chill_guy}"
    k = "4213"
    print (shift_encode(m,k))

例：(k=3)

1 2 3 4 5 6 7 8 9

147 258

{}

像是一個寬度為k的柵欄總共會有k個柵欄
python code:

def shift_encode(m,k):
    c = ""
    for i in range(0, len(m), len(k)):
        m1 = [""]*len(k)
        if i+len(k) > len(m):
            temp = m[i:]
        else:
            temp = m[i:i+len(k)]
        for j in range(len(temp)):
            m1[int(k[j])-1] = temp[j]
        c += "".join(m1)
    return c

if  __name__ == '__main__':
    m = "melonCTF{cuz_i_am_a_chill_guy}"
    k = "4213"
    print (shift_encode(m,k))

例：(k=3)

1 2 3 4 5 6 7 8 9

147 258 369

{}

像是一個寬度為k的柵欄總共會有k個柵欄
python code:

def shift_encode(m,k):
    c = ""
    for i in range(0, len(m), len(k)):
        m1 = [""]*len(k)
        if i+len(k) > len(m):
            temp = m[i:]
        else:
            temp = m[i:i+len(k)]
        for j in range(len(temp)):
            m1[int(k[j])-1] = temp[j]
        c += "".join(m1)
    return c

if  __name__ == '__main__':
    m = "melonCTF{cuz_i_am_a_chill_guy}"
    k = "4213"
    print (shift_encode(m,k))

例：(k=3)

1 2 3 4 5 6 7 8 9

147 258 369

解密：窮舉K即可反推

{Rail Fence Cipher}

像是一個寬度為k的柵欄總共會有k個柵欄

例：(k=3)

1 2 3 4 5 6 7 8 9

解密：窮舉K即可反推

1				5				9
	2		4		6		8
		3				7

C = 159

{Rail Fence Cipher}

像是一個寬度為k的柵欄總共會有k個柵欄

例：(k=3)

1 2 3 4 5 6 7 8 9

解密：窮舉K即可反推

1				5				9
	2		4		6		8
		3				7

C = 1592468

{Rail Fence Cipher}

像是一個寬度為k的柵欄總共會有k個柵欄

例：(k=3)

1 2 3 4 5 6 7 8 9

解密：窮舉K即可反推

1				5				9
	2		4		6		8
		3				7

C = 159246837

{替代密碼}

{caesar cipher}

將每個字元位移k個超過範圍會從頭開始
超級常見但是每個要求的不一樣
- 例如：
  - 只轉換a-z,A-Z
  - 轉換ascii
  - 更多變換
- 加密邏輯：for i in m: c+= chr((ord(i)+k)%128)
- 解密邏輯：for i in m: c+= chr((ord(i)-k)%128)

{caesar cipher}

攻擊手法：
- 字頻分析：etaoin shrdlu cmfwyp vbgkjq xz
- 詞頻分析：
  - 一般句子中常見： "the" "be" "of" "and" 等等
  - CTF中最常見的就是"Flag"了(不同比賽的flag name不同)
- 暴力枚舉：K最多就26 或者 128 用眼睛就能看出(爆搜)
ROT13:前後調換

{Vigenère Cipher}

密鑰變字串
密鑰ᵢ作為明文ᵢ的offset i超過len(密鑰)從頭開始

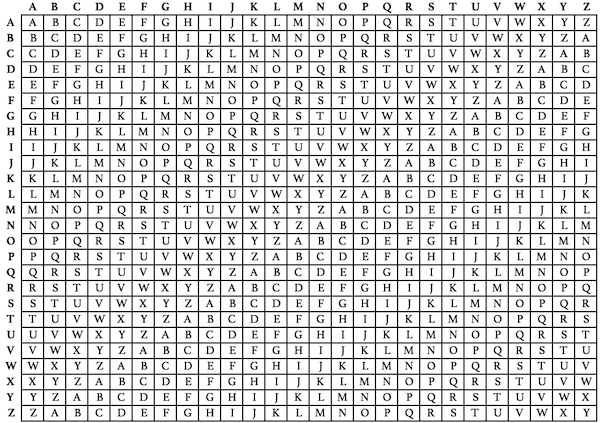
{Vigenère Cipher}

攻擊手法：
- 卡西斯基試驗(Kasiski examination)(先提出)
  - 長文本中可能有常用詞(ex:the) 被同一段密鑰加密產生重複子字串
  - 用字串間的距離的最小公因數推算K的長度

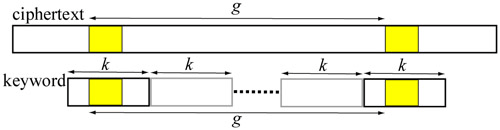
{Vigenère Cipher}

攻擊手法：
- 弗里德曼試驗(Friedman examination)(後提出)

太費腦了反正就人家算出來的結果

透過前面推算出來的密鑰長度
- Mₙₖ₊ᵢ都是對應到Kᵢ
- 很像像前面提過的的跳K個
- 把Mₙₖ₊ᵢ都分給Kᵢ加密然後各自分析出語義正確的答案
工具：
- CyberChef(再次出現)
- Cryptii(也有很多工具，需密鑰)
- vigenere-solver
  - 不需密鑰藉由前面提到的原理推算明文
  - 不一定會猜對

{頻率分析}

{Pigpen Cipher}

{Affine Cipher}

這次不講大抵上是用線性同餘

Morden

cipher

現代密碼

{XOR}

對稱加密
現代密碼學的基礎
容易運算低成本好懂
原理：
- XOR
- M ⊕ K = C 則 C ⊕ K = M
本身密碼強度不高：
- 容易被頻率分析
- 已知明文 =>密鑰洩漏
把密鑰改成(偽)隨機的：
- 串流加密法：K=隨機seed->random(K)->線性同餘->C

a	b	a^b
1	0	1
0	1	1
1	1	0
0	0	0

{RSA}

前情提要
模(Mod) ：a / b = c ... d ，則 a mod b = d

模逆：在a × x = 1 (mode k)的情況下求x

同餘
- a mod c = k 且 b mod c = k
- 則 a ≡ b (mod k)
歐拉函數 φ(n) : 小於或等於n的正整數中與n互質的數的數目

{RSA}

操作-生成公鑰&私鑰

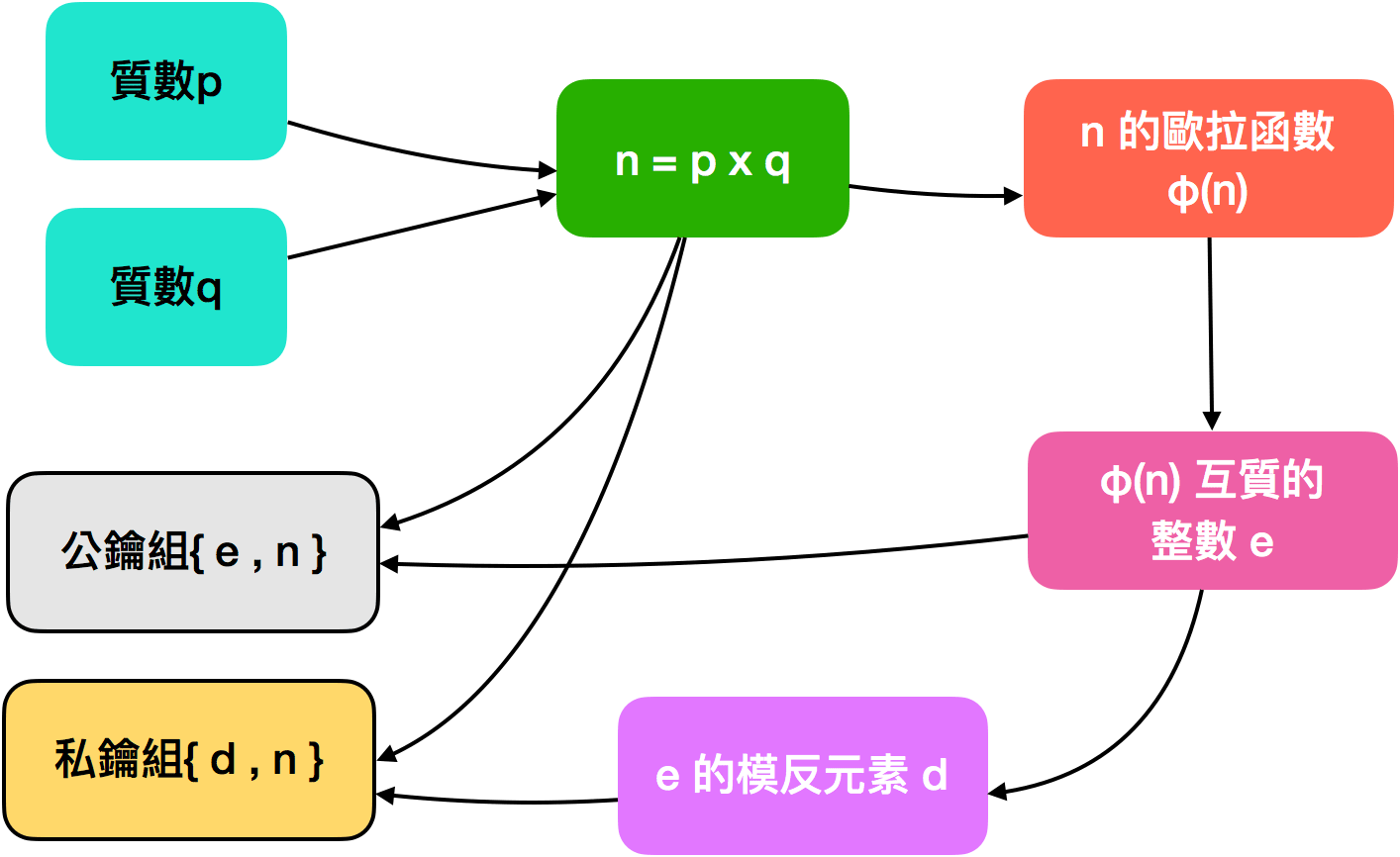
{RSA}

操作-加密＆解密

\left\{ \begin{matrix} 加密：C = M^e & mod&N\\ 解密：M = C^d & mod&N \end{matrix} \right.

N = (p-1)(q-1) =\varphi(n) = \varphi(p \cdot q)

{RSA}

非對稱加密
柯克霍夫原則：
- 數學上可以破解但實用程度低
安全性：
- 有可能從公鑰 { e , N }反推私鑰嗎？
  - ed ≡ 1 (mod N) （模逆元）=>要知道d必須知道N的值
  - N = (p - 1)(q - 1) 在p q很大時難以計算
  - 質因數分解大數需要極長時間=>安全性保障

RSA是這三個老哥的名子開頭

{platforms}

{PicoCTF}

CTF解題平台
題目有分類分難度
解題有提示 Writeup多如山新手友好(?)
定期有比賽電到發慌可以去打(揪?)

怎麼有點4K

{PicoCTF}

註冊連結
老樣子能不填就不要填不會填直接問

{PicoCTF}

加入PicoCTF classroom
Invite Code：CTcN70z2P

{題單}

interencdec
Mod 26
The numbers
13
base

{CTFtime}

註冊連結
由於CTF比賽多到爆
- 很多比賽會在CTFtime上登記(?)
然後如果你電到發慌就可以上去找找要打哪個

{reference}

https://gchq.github.io/CyberChef/

https://hexed.it/
https://enkhee-osiris.github.io/Decoder-JSFuck/
https://ithelp.ithome.com.tw/articles/10352123
https://techapple.com/archives/25855
https://zh.wikipedia.org/zh-tw/%E6%9F%AF%E5%85%8B%E9%9C%8D%E5%A4%AB%E5%8E%9F%E5%89%87
https://wecan.tw/index.php/2018-12-02-08-34-31/2019-01-03-18-18-31/4000words-frequency
https://blog.csdn.net/QAZJOU/article/details/125940393
https://albert-notes.github.io/2023/01/26/ctf-crypto-1/
https://slides.com/lucasw/wtf_code
https://blog.techbridge.cc/2016/07/16/javascript-jsfuck-and-aaencode/
https://juejin.cn/post/7182513893325930557
https://gist.github.com/wh1t3p1g/ffd15270914492491e18ff9f070eab2b
https://ithelp.ithome.com.tw/m/articles/10215106
https://zh.wikipedia.org/wiki/%E7%B7%9A%E6%80%A7%E5%90%8C%E9%A4%98%E6%96%B9%E6%B3%95

CTF-Crypto

By idoit_melon

CTF-Crypto

who am i?

西瓜

Index

intro

Problems

Practice

Crypto-intro

{Crypto}

Crypto 密碼學(cryptology)

真正的Crypto高手只要一張紙一支筆以及Python環境就可以稱霸全場了

{Crypto}

分類

{Crypto}

分類

{Encode}

{Encode}

編碼

定義

​種類五花八門，不用全會

{Encode}

kea is so dian

a2VhIGlzIHNvIGRpYW4=

{反函數}

可以簡單理解為輸入輸出交換

{​Morse Code}

摩斯密碼

{​Hex}

十六進制

{​carry system}

Dec(十進位)

{​carry system}

Hex(十六進位)

{​Hex->Dec}

轉換方法

{​Dec->Hex}

轉換方法

{​Hex->Str}

轉換方法

{​Urlencode}

瀏覽器跟網站傳送資料時解決特殊字符

{​BrainFuck}

腦幹

{​BrainFuck}

腦幹

{​BrainFuck}

腦幹

{​BrainFuck}

腦幹

JS幹

JS幹

JS幹

{​Base-X}

以X個字元來表示二進位資料 有剩餘的補"="

🉐 每3個ascii字母可以encode成4個字元

{​Base-X}

以X個字元來表示二進位資料 有剩餘的補"="

{​Base-X}

{​柯克霍夫原則}

即使密碼系統的任何細節已為人悉知，只要密匙（key，又稱金鑰或金鑰）未洩漏，它也應是安全的。

{​密碼學分類}

對稱加密：大多古代密碼

同一把密鑰

{​密碼學分類}

非對稱加密：大多數現代密碼

{​密碼學分類}

非對稱加密：大多數現代密碼

{​密碼學分類}

非對稱加密：大多數現代密碼

防止公鑰被洩漏而有資安風險

Classical cipher

{位移密碼}

{簡單位移密碼}

直接舉例(M=明文，K=密鑰，C=密文)

{簡單位移密碼}

特徵：

{}

像是一個寬度為k的柵欄 總共會有k個柵欄

{}

像是一個寬度為k的柵欄 總共會有k個柵欄

種類五花八門，不用全會

{Morse Code}

{Hex}

{carry system}

{carry system}

{Hex->Dec}

{Dec->Hex}

{Hex->Str}

{Urlencode}

{BrainFuck}

{BrainFuck}

{BrainFuck}

{BrainFuck}

{Base-X}

以X個字元來表示二進位資料有剩餘的補"="

{Base-X}

以X個字元來表示二進位資料有剩餘的補"="

{Base-X}

{柯克霍夫原則}

{密碼學分類}

{密碼學分類}

{密碼學分類}

{密碼學分類}

像是一個寬度為k的柵欄總共會有k個柵欄

像是一個寬度為k的柵欄總共會有k個柵欄

像是一個寬度為k的柵欄總共會有k個柵欄

像是一個寬度為k的柵欄總共會有k個柵欄

像是一個寬度為k的柵欄總共會有k個柵欄

像是一個寬度為k的柵欄總共會有k個柵欄

像是一個寬度為k的柵欄總共會有k個柵欄

像是一個寬度為k的柵欄總共會有k個柵欄

{caesar cipher}

將每個字元位移k個超過範圍會從頭開始

{caesar cipher}

{Vigenère Cipher}

{Vigenère Cipher}

{Vigenère Cipher}

弗里德曼試驗(Friedman examination)(後提出)

把Mₙₖ₊ᵢ都分給Kᵢ加密然後各自分析出語義正確的答案

{XOR}

{RSA}

{RSA}

{RSA}

{PicoCTF}

{PicoCTF}

{PicoCTF}

{題單}

{CTFtime}