Randomized Loose Renaming in
O(log log n)
Time
irving cordova
What is renaming?

"Distributed coordination task in which a set of processes must pick distinct identifiers from a small namespace"
Why is it important?

- renaming is the other side to consensus
- consensus: processors agree on a single value
- renaming: processors disagree in that each has a distinct value
Why is it important?
(cont.)

- Assigning work without a master
- Distributing capabilities
Kinds of renaming

- non-adaptive
- strong
- loose
- adaptive
Non-adaptive renaming

Maximum number of processes n is known and each process must obtain a unique name from a target namespace of size m
Strong / loose renaming

Renaming is strong (or optimal)
if the namespace m is equal to n
It's opposite is:
Loose Renaming
Adaptive renaming

The size of the namespace depends on the contention (k) in the current execution
Adaptive renaming
(cont.)
In other words, (k) depends on the number of processors
that take steps concurrently in this operation.
Previous work
D. Alistarh, et al.
gave a lower bound
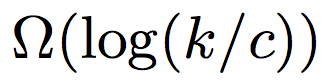
where c is a constant >= 1
Previous work
(cont.)
The result suggested a logarithmic complexity threshold for adaptive renaming
Enter randomization

In Principles of Distributed Computing 2013, Dr. Dan Alistarh et al. showed how they used randomization to solve the renaming problem.
Enter randomization
(cont.)
They proved:
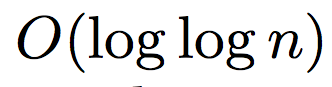
and
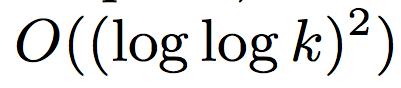
for adaptive renaming.
Restricting the model
- Asynchronous shared memory.
- Shared memory supports Test & Set operations (TAS).
The rebatching algorithm
Implementing the algorithm

- Atomic Integer
- Java threads
Visualizing execution
Originally wanted to show the visualization of the algorithm visually.
Unfortunately swing is not thread-safe, so it proved to be a processing bottleneck.
Let's run it
Difficulties

- Algorithm needs a high number of TAS registers
- Constant for namespace restricted because of memory.
Difficulties
(cont.)
- Bucket part of the algorithm never kicked in.
Results

- Executions: 50
- Processors: 2^15
- Avg total time: 160ms
- Slower processor: 9ms
- Avg execution time: 0ms
Improving rebatching

- What if the backup phase didn't start from index 0?
- Start backup faster.
- Start backup phase from random number.
- The level of contention should be smaller.
Results

- Executions: 15
- Processors: 2^15
-
Avg total time: 160ms
-
Slower processor: 20ms
- Avg execution time: 0ms
Results
(cont.)
- No discernible improvement over rebatching.
- Better than naive rebatching.
- In normal rebatching, almost no processors go into the backup phase.
- The average time to acquire a name is pretty fast, so it is likely most time is spent on thread creation.
Future Work

- Memory consumption is too high with this algorithm.
- CPU was not the bottleneck.
-
Use mutual exclusion to provide access to a name dictionary and reduce number of registers needed.
Future work
(cont)

- Implement the Adaptive Rebatching algorithm.
- Analyze whether the bucket size can be reduced.
Questions

Sources
- D. Alistarh, G Giakkoupis, J. Aspnes, P. Woelfel. Randomized Loose Renaming in O(log log n) Time PODC 2013.
- Y. Afek, H. Attiya, A. Fouren, G. Stupp, and D. Touitou. Long-lived renaming made adaptive. In Proc. of 18th PODC, pages 91-103, 1999.
Thank You
Irving Cordova
Addendum
Upon further investigation the cause for the algorithm not improving with the changes, was that in average only 1.5% of the processors go into the backup phase.
(charts in next slide ->)
Addendum
(cont)
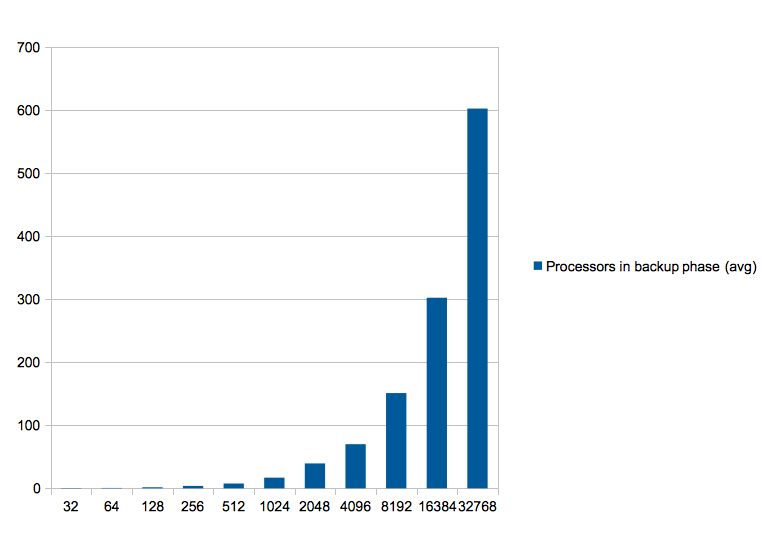
Addendum
(cont)
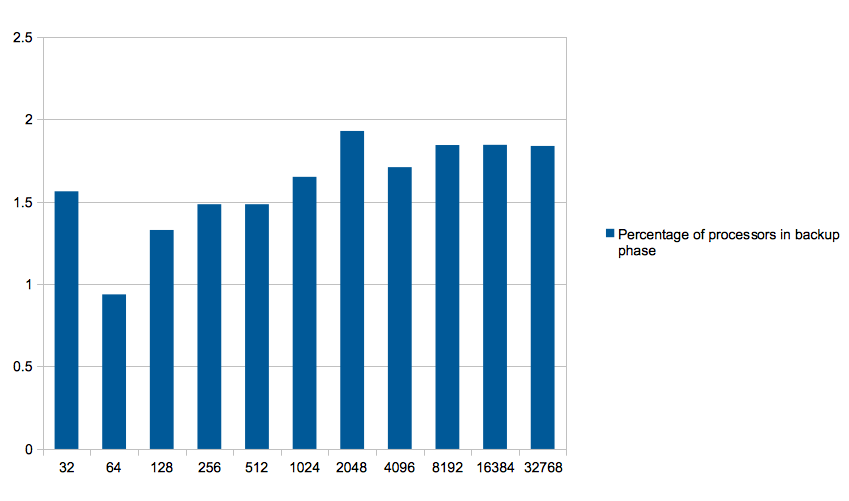
Addendum
(cont.)
Even though there was improvement with the changes, it is so small as to not make any significant difference at run-time.
Randomized Loose Renaming in O(log log n) Time
By Irving Cordova
Randomized Loose Renaming in O(log log n) Time
- 986



