Comunicación ordenada y confiable

Maestría en Ciencias Computacionales
Irving N. Llamas Covarrubias
TC4003 - Octubre 2017
HECTOR GARCIA-MOLINA, ANNEMARIE SPAUSTER
August 1991

Agenda
- Contexto
- El problema
- Soluciones existentes
- Solución propuesta
- Rendimiento
- Fiabilidad y grupos multicast dinámicos
- Conclusiones
1. Contexto

Grupo multicast
Colección de procesos que son el destino de la misma secuencia de mensajes.
Mensajes se pueden originar en uno o mas sitios, y el destino puede ser uno o más sitios, no necesariamente distintos.
Los grupos multicast se pueden traslapar

Protocolo multicast
Responsable de entregar mensajes a los procesos apropiados.
Algunas aplicaciones requieren que el protocolo garantice el orden en el que los paquetes son entregados.

Propósito de la investigación
Orden de grupos múltiples:
Propiedad que garantiza que dos mensajes destinados a dos procesos son entregados en el mismo orden relativo, incluso si se originan de diferentes fuentes y están dirigidos a diferentes grupos multicast.
Se presenta protocolo
Propagation Graph Algorithm
Resuelve problema de ordenamiento de grupos múltiples.

2. El problema


Comunicación de un grupo multicast

Propiedades de un protocolo multicast
Si los mensajes m1 y m2 se originan desde el mismo sitio, y están dirigidos al mismo grupo multicast. Entonces, todos los procesos destino obtienen el mismo orden relativo.
A)Ordenación de origen único

Propiedades de un protocolo multicast
Si los mensajes m1 y m2 están dirgidos al mismo grupo multicast. Entonces, todos los procesos destino obtienen el mismo orden relativo (Incluso si vienen de diferentes origenes).
B)Ordenación de origen múltiple

Propiedades de un protocolo multicast
Si los mensajes m1 y m2 se entregan a dos procesos, se entregan en el mismo orden relativo.(Incluso si vienen de diferentes fuentes y están dirigidos a grupos multicast diferentes pero superpuestos).
C)Ordenación de grupo múltiple

Ejemplo 1





Computadora principal
Computadora respaldo
Sucursales
B) Transacciones deben ejecutarse en el mismo orden en las computadoras principales, o el estado de la base de datos será diferente.

Ejemplo 2





Computadora principal
Computadora respaldo
Sucursales
C) Aunque están involucrados dos grupos multicast separados. Sigue siendo importante procesar todos los mensajes en el mismo orden en las máquinas en la intersección de los grupos.



Máquinas desarrollo



3. Soluciones existentes

Garantizar la propiedad A de un protocolo multicast es relativamente simple.
La aplicación de múltiples fuentes y propiedades de grupo es más difícil.(B y C)

Timestamp
A
B
C
D
E
F
X
Y
Z
Cuando el sitio C recibe m1 no puede entregarlo inmediatamente a su proceso destino. Primero debe descubrir de todas las fuentes potenciales, si existen mensajes con marcas de tiempo más pequeñas.
Solo cuando un sitio está seguro de que un mensaje tiene la marca de tiempo más pequeña de cualquier mensaje no entregado, lo entrega.
Figura1



Two-Phase commit

- El remitente envía el mensaje a todos los destinos del grupo multicast.
- Cada receptor le da su propio número de prioridad. El cuál es un número único en el sistema más alto que cualquiera dado hasta ahora para ese proceso.
- Mensaje se marca como "no entregable" y se coloca en la cola.
- Cada receptor devuelve el número asignado al remitente.
- El remitente selecciona el número más alto que recibió y lo envía a los receptores, los cuáles reemplazan el original por el nuevo que se recibio, y lo marcan como "entregable".
- Cada receptor reordena la cola.
- Cuando un mensaje está en la parte delantera de la cola y esta marcado como "entregable", se entrega.
Nota: Cada sitio mantiene una cola de prioridad por proceso.
Birman y Joseph

Central site
Los dos enfoques anteriores son completamente distribuidos y pueden tener importantes gastos de mensajes.
Para reducir costo de sincronización. Todos las fuentes transmiten a un sitio central, el cuál asigna una secuencia de números a los mensajes y los reenvía a los sitios de destino.
El sitio central se identifica con un tóken, y con el tiempo, este tóken circula a través del sistema.
Chang y Maxemchuk
4. Solución propuesta


La investigación propone una nueva solución para garantizar la propiedad C. Para ello se expone el Propagation Graph Algorithm
Se sume que la red y los nodos no fallarán
Algoritmo inspirado en el de Chang and Maxemchuk
En lugar de ordenar todos los mensajes en un sitio central, se ordenan como una colección de nodos estructurados en un grafo de propagación de mensajes(En un bosque). En donde cada nodo en el grafo representa una computadora.

El grafo indica las rutas que los mensajes deben seguir para llegar a todos sus destinos.
En lugar de enviar los mensajes a los destinos y luego ordenarlos. Los mensajes se propagan a través de una serie de sitios que los ordenan en el camino mediante la unión de mensajes destinados a diferentes grupos.
Cuando un sitio recibe un mensaje, se entera de inmediato cuál es el orden que le pertenece y espera los mensajes anteriores antes de entregarlo al proceso destino. La idea clave es usar los sitios que esán en las intersecciones de los grupos de multidifusión como los nodos intermedios.

A
B
C
D
E
F
X
Y
Z


+


Figura2
Todos los sitios entregan sus mensajes en el orden definido por el sitio C.
El sitio C envia los mensajes que corresponden a alfa{A,B} y los que corresponden a beta{E,F}. Por último los mensajes unidos de alfa y beta a {D}.
El algoritmo de propagación que se propone tiene 2 componentes:
- El generador de grafo de propagación (PG)
- El protocolo de paso de mensajes (MP)

Por simplicidad se asume que un sitio corre el generador PG y transmite el resultado a los otros sitios.
Una ves que un sitio conoce el grafo, utiliza el protocolo MP para enviar,recibir, prograpar y reenviar mensajes.
Terminología:
Fuente: Sitio que origina el mensaje para el grupo multicast.
Grupo de destino: Grupo que recibira los mensajes.
Destino principal: Cuando la fuente envía un mensaje a un sitio del grupo multicast(Incluso puede ser la misma fuente).

A
B
C
D
E
F
G
H
J
Figura3
Un ejemplo mas complicado, con 9 sitios (A,B,C,D,E,F,G,H,J) y 8 grupos de destino:
1 = {C,D}
2 = {A,B,C}
3 = {B,C,D,E}
4 = {D,E,F}
5 = {E,F}
6 = {B,G}
7 = {C,H}
8 = {D,J}
Nota: Los mensajes no fluyen necesariamente hacia la parte baja del árbol. Por ejemplo G solo recibe los mensajes del grupo 6.

Garantiza
Generador PG
Propiedades
- Propiedad C de un protocolo multicast.
- Si x pertenece al grupo alfa, entonces x toma todos los mensaje destinados a alfa.
(PG1) Para cada grupo alfa existe un solo destino primario p.
(PG2) Para cada sitio x que pertenece a alfa, existe un único camino de p a x.
Propiedades opcionales
(PG3) El destino primario de un grupo alfa es miembro de alfa.
(PG4) Sea p el destino primario de alfa y x otro sitio en alfa. Entonces, los nodos en el camino de p a x son todos miembros de alfa.
El generador PG garantiza la propiedad PG3, pero desafortunadamente algunas veces genera un nodo extra.
Un nodo extra es, cuando existe un nodo a en la ruta de p a x donde a no es parte de alfa.

Generador PG
* El generador PG selecciona el sitio con el número más grande de grupos (D en nuestro ejemplo) y lo convierte en la raíz. Esta heurística ayuda a mantener cortos los árboles en el bosque.
* Se llaman grupos a los que pertenece la raíz, grupos raíz a los otros sitios en los grupos raíz intersecters . La raíz es entonces el destino primario para todos los grupos raíz.
main (”)
begin
groups = the set of multicast groups;
sites = the set of sites;
unmarked–groups = groupsr;
unmarked–sites = sites;
while unmarked–groups( )
{
root = s | s occurs most frequently in unmarked–groups;
new–subtree(root);
}
end
new–subtree(current–subroot)
begin
intersecters = emptySet;
/* Marque el sitio desde que se colocó en el bosque. */
mark–site (current–subroot);
/* Determine los sitios que están en los grupos con la subraíz. */
for each s isIn unmarked-sites
if Some(g) isIn unmarked–groups such that (s inIn g ^ current–subroot isIn g)
then
intersecters = intersecters U s;
/* Marque todos los grupos que contienen la subraíz ya que ahora tenemos un destino principal para ellos.*/
for each g isIn unmarked-groups
if current–subroot isIn g
then
mark–group( g );
/* Particiona grupos para que ningún grupo en una partición instersecte un grupo en otra partición
y algún sitio en algún grupo de cada partición, se incluye un grupo con la sub-raíz(Esta en intersecters)*/
G = {g | g isIn unmarked-groups ^ some(s) isIn g such that s isIn intersecters};
repeat
S = {s | some(g) isIn G such that s isIn g}
G = G U {g | g isIn unmarked-groups V some(s) isIn G such that s isIn S}
until no change to G
P1, . . . Pk = partition of G so that no group in a partition intersects a group in another partition;
/*Si s está en un grupo de la raíz pero no es parte de una partición, se convierte en hijo.*/
for each s isIn intersecters
if s is not in P_l
current-subroot = s; /*makes a child ofcurrent-subroot*/
/*Determina un hijo para cada partición*/
for i:= 1 to k
newsite = s | s occurs most frequently in P_l ^ s isIn intersecters;
current–subroot = newsite; /* make newsite a child of current–site */
new–subtree (newsite);
end
mark–site(s)
begin
unmarked–sites = unmarked–sites – s;
end;
mark–group(g)
begin
unmarked–groups = unmarked–groups – g;
end;
Generador PG
*En el ejemplo para P1 b y c ocurren en la mayoría de todos los grupos, entonces arbitrariamente se eleige c sobre b. Arbitrariamente también se toma e sobre f. En algunos casos existirán sitios que son intersecters pero no ocurren en ninguna partición, como en este caso j, entonces automáticamente se convierten en hijos de la raíz.
*Para generar el siguiente nivel se llama new_sub-tree para cada hijo, con el hijo como parámetro.
(A,B,G,H)
C
D
E
F
J
Figura4

Protocolo MP
El grafo de propagación especifíca el flujo de los mensajes en la red. El destino principal para cada grupo multicast es el más cercano a la raíz.
El protocolo requiere que cada sitio mantenga una numeros de secuencia para cada sitio al cuál envía mensajes, como se determino en el grafo de propagación. Esto garantiza que el receptor puede ordernar los mensajes del emisor correctamente en caso de que lleguen en desorden. Esto igual ayuda s la dectección de pérdida de mensajes. ACK no son requeridos por el protocolo. Null y timeouts son usados para detección de fallos.
En cada sitio se mantienen dos colas, una cola para mensajes destinados a un proceso local y una cola de espera para mensajes que llegan fuera de secuencia.
5. Rendimiento

El rendimiento es una medida crucial para la practicidad del algoritmo de propagación. Aqui se comparará con el de two-phase de Birman y Joseph y con el estrictamente centralizado de Chang y Maxemchuck.

Redes tipo ARPANET. Una sola fuente envía el mismo mensaje a n sitios. Se envían n mensajes, uno para cada receptor.
Modelo Punto a punto
| two-phase | Centralizado | Propagación | |
|---|---|---|---|
| N | 3n | n | n + e |
| D | 3L+(2n+1)P | 2L+nP | (d+1)L+(n+e)P |
N: Número mensajes requeridos para enviar al grupo multicast.
D: Tiempo transcurrido entre el comienzo de la difusión, y la finalización de la misma.
d: Profundidad esperada
L: Latencia
P: Procesamiento
e: Nodos extra
n:Número de mensajes

Modelo Punto a punto
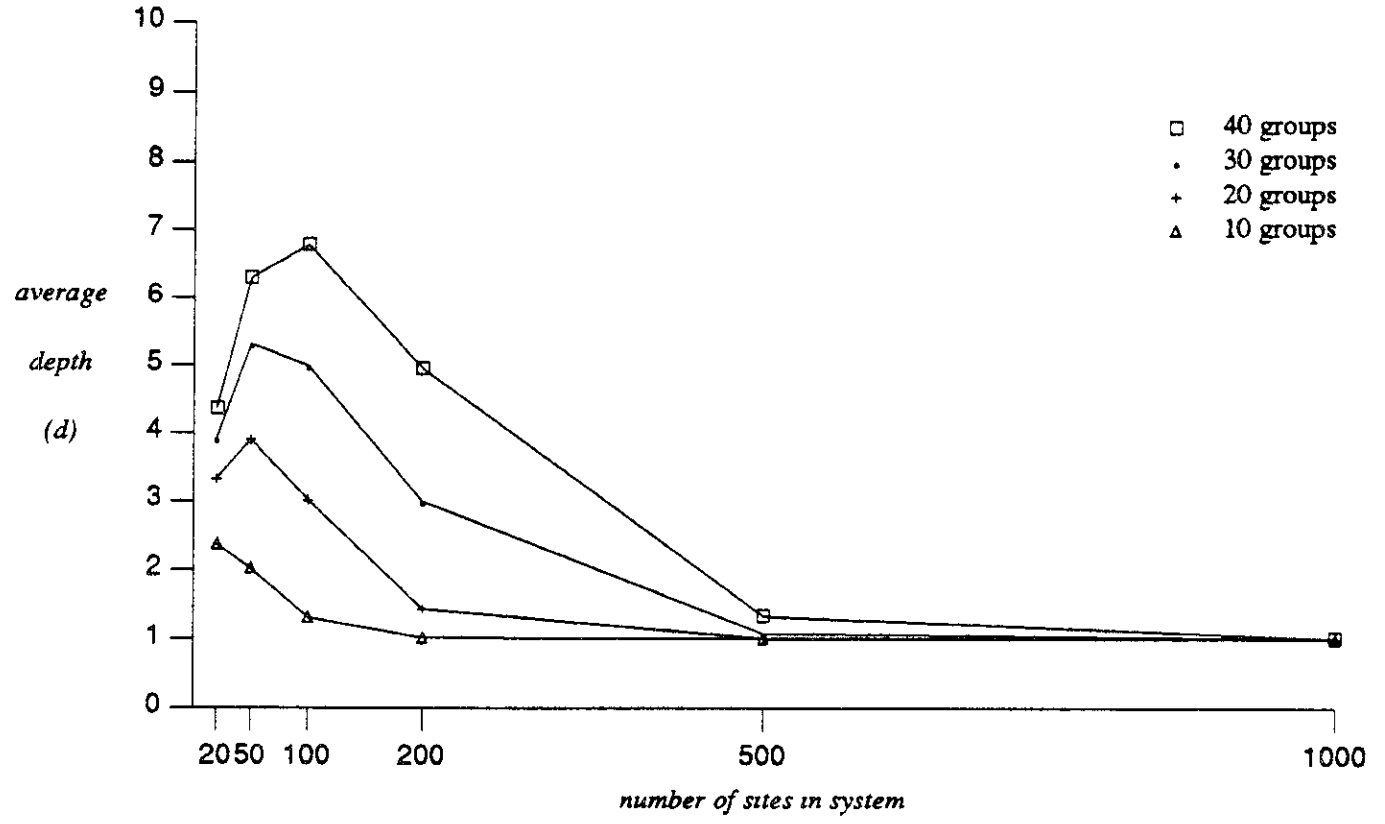
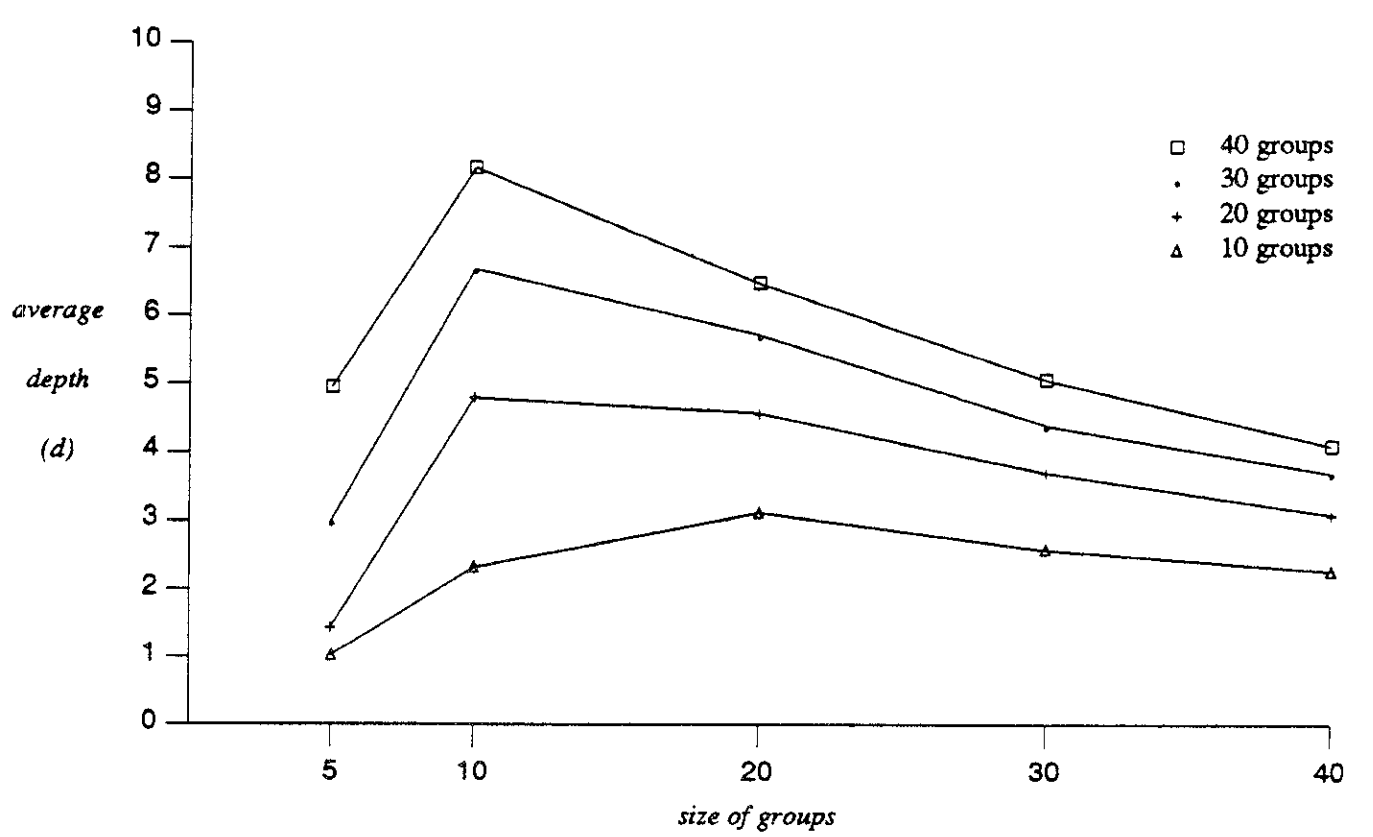
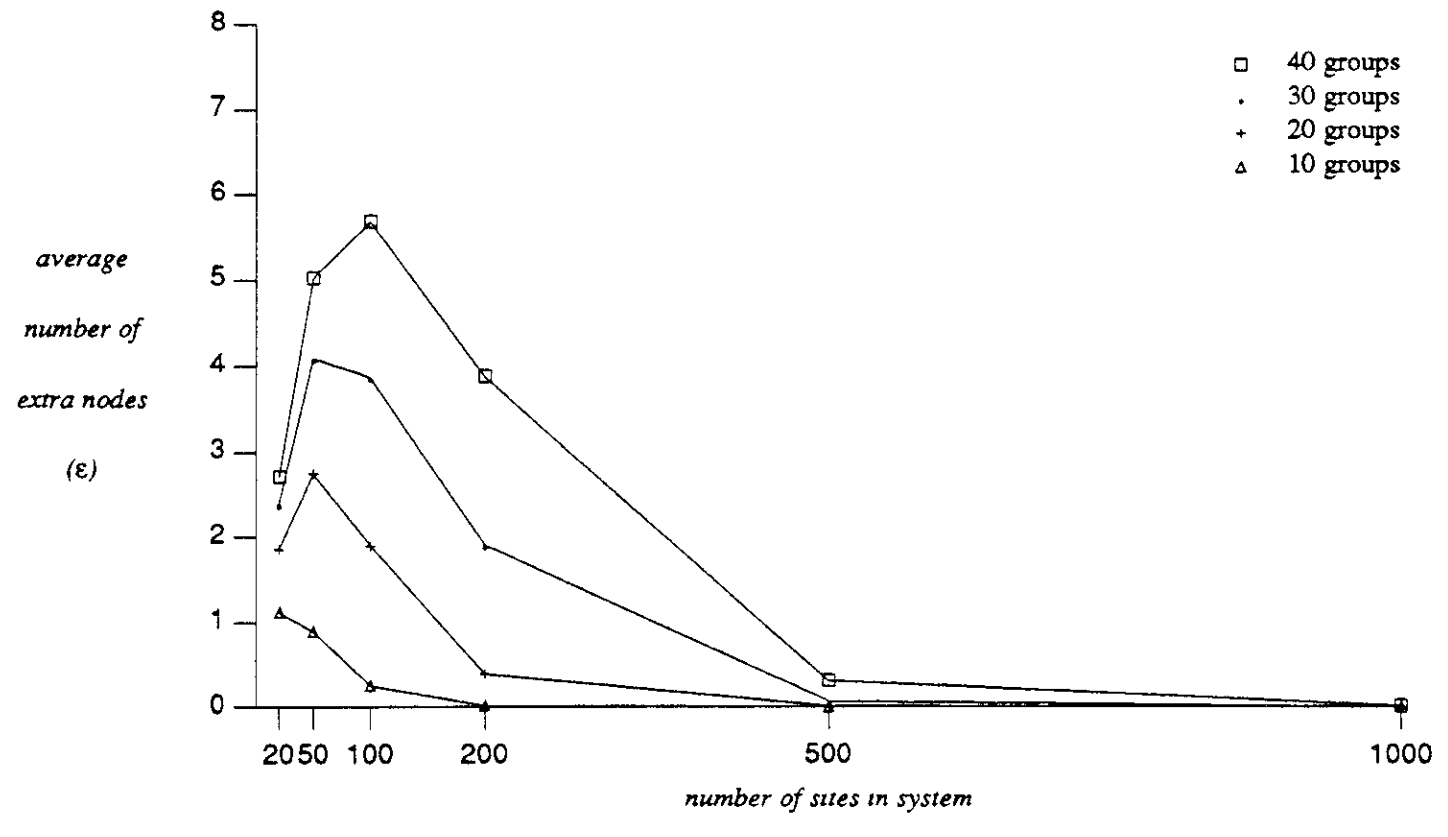
Tamaño de grupo 5.
200 sitios en el sistema
Tamaño de grupo 5.

Modelo Punto a punto
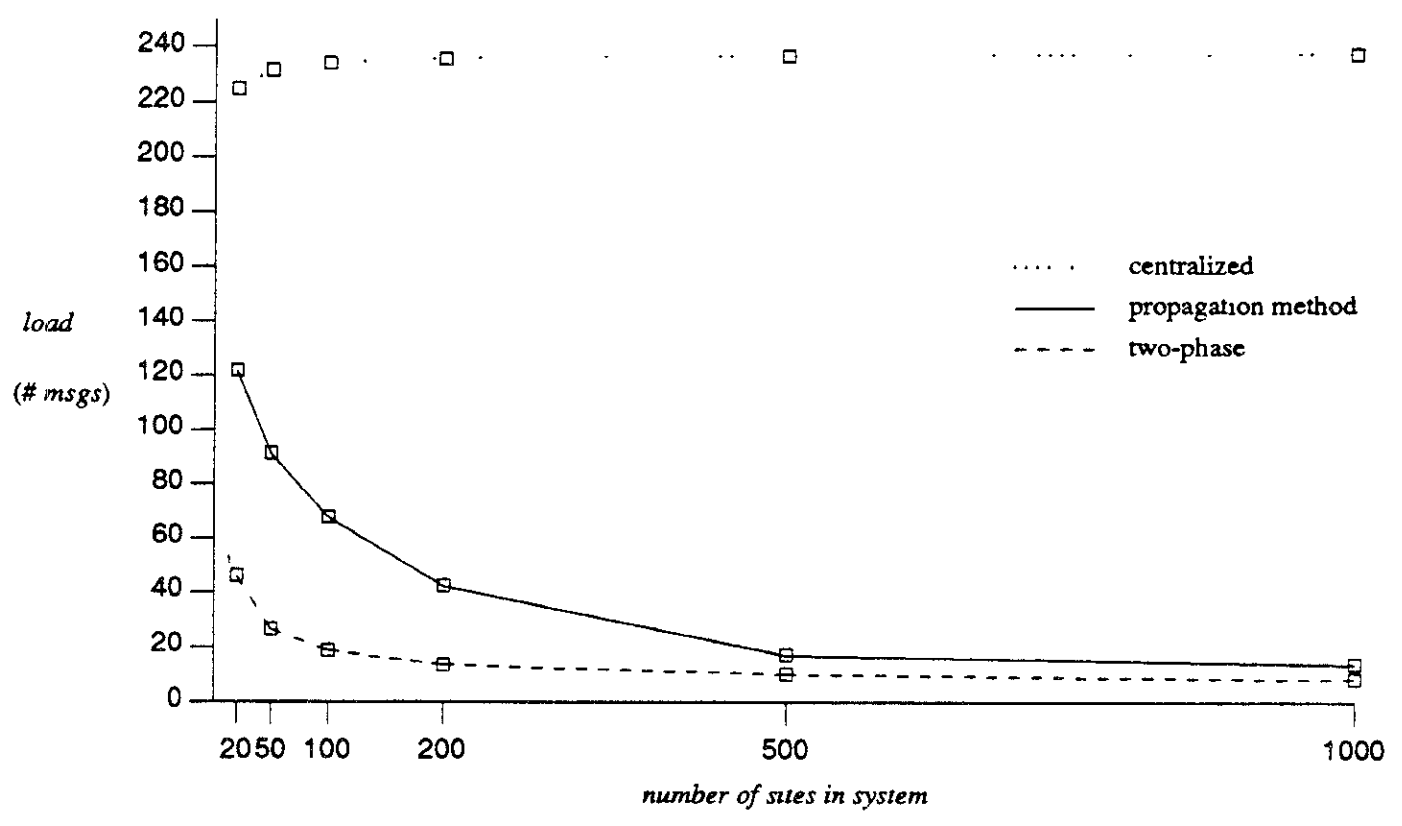
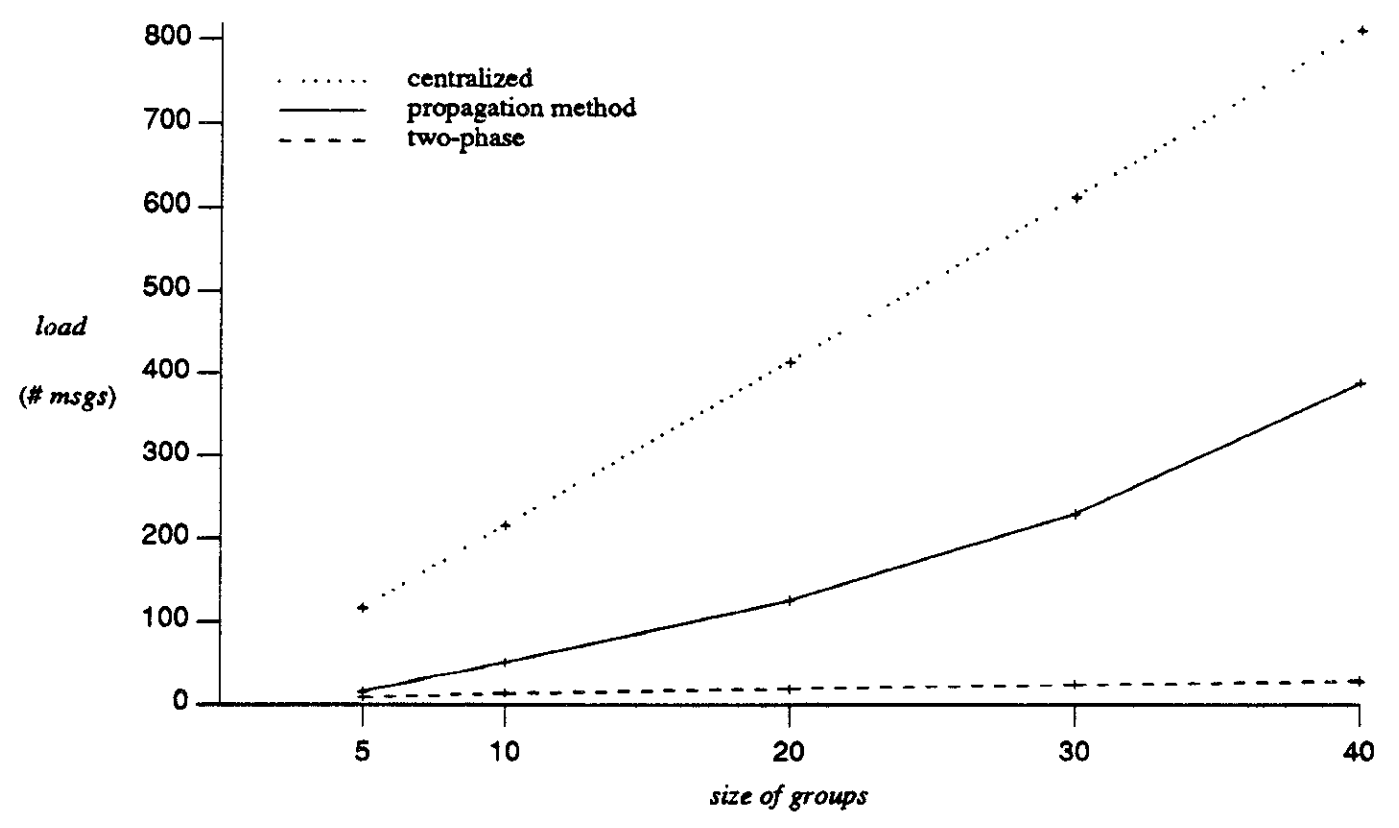
Tamaño de grupo 5.
200 sitios en el sistema

Modelo Broadcast
Redes tipo Ethernet. Un mensaje enviado por una fuente es transmitido a todos los sitios en la red a la vez.
| two-phase | Centralizado | Propagación | |
|---|---|---|---|
| N | n+2 | 2 | d+1 |
| D | (n+2)T | 2T | (d+1)T |
T: Demora que consiste en
Tiempo para que el remitente coloque el mensaje en la red
+Tiempo para que el mensaje llegue a los otros sitios
+Tiempo para que cada sitio determine si es miembro del grupo destino.
d: Profundidad esperada
n:Número de mensajes
6. Confiabilidad y grupos multicast dinámicos

El algoritmo expuesto es correcto cuando no existen fallos y el grupo multicast es estático. Sin embargo es necesario considerar las fallas de los sitios y de la red.

Se desarrollo un modelo para el problema de confiabilidad en el algoritmo. En el cuál se menciona que no se consideran fallas bizantinas y se asumen que los relojes son sincronizados. Además el modelo puede ser confiable en varios grados.
Confiabilidad

La fiabilidad de un protocolo puede caracterizarse por sus propiedades P,Q,R.
Confiabilidad
P: Garantía en la entrega de un multicast en algunos miembros del grupo de destino.
Q: Garantía sobre la atomicidad de la entrega entre los miembros del grupo.
R: Interacción entre la confiabilidad y el orden.

Confiabilidad en PG
P: Sea m un mensaje multicast por s. Sea r el tiempo que el sitio s envia m a a(la raíz), como parte del protocolo. Existe una constante delta tal que si a y s están activos de un periódo X a X + delta y a y s pueden comunicarse de tiempo X al tiempo X + delta, para algunos X >= t, entonces a entrega m con X + delta.

Confiabilidad en PG
Q: Sean m los mensajes multicast por s y digamos que m ha sido enviado a un miembro del grupo a. Si el padre de b p(b) entrega m en tiempo alfa, entonces existe una p tal que si b y p(b) pueden comunicarse desde el tiempo X al tiempo X + p, por algun X >= alfa, entonces b entrega m en el tiempo X + p.

Confiabilidad en PG
R: No hay 2 sitios que entreguen mensajes en ordenes incoherentes. Llamamos a esto garantía totalmente consistente porque la orden se aplica estrictamente a todos los destinos. Tal condición requiere bloquear la propagación de mensajes en el árbol cuando falla un sitio que no es hoja.

Grupos dinámicos
La reorganización del árbol no solo resulta de fallas. Algunas veces simplemente se quieren agregar nuevos sitios a los grupos o eliminar sitios de grupos.
Una falla puede ocurrir en medio de la reorganización de los árboles. Sitios ya sea en el árbol viejo o en el nuevo detectarán la falla de un padre e informaran a la raíz anterior.
7. Conclusiones


Positivo
En la mayoría de los casos es superior al algoritmo two-phase en término de número de mensajes.
Elimina el problema de cuello de botella que se origina en el centralizado.
Proporciona flexibilidad al permitir diferentes grafos para el mismo conjunto de grupos para adaptarse a los requisitos de la red o aplicación.


Negativo
El costo de configuración del grafo de propagación, por lo tanto, la técnica debe usarse para streams multicast que son de larga duración.
Algunas veces los sitios requieren manejar mensajes que no necesitan entregar localmente. Estos nodos extra, no ocurren con frecuencia de acuerdo a los experimentos realizados.

Bibliografía

Ordered and reliable multicast communication. Hector Garcia-Molina, AnneMarie Spauster.
Aug. 1991
Comunicación ordenada y confiable
By Irving Norehem Llamas Covarrubias
Comunicación ordenada y confiable
- 341



