基礎DP
什麼是DP?
舉個例子
費波那契數列
由0和1開始
之後由前兩位數字相加而得出
第n項為第n-1和第n-2項的總和
用遞迴試試
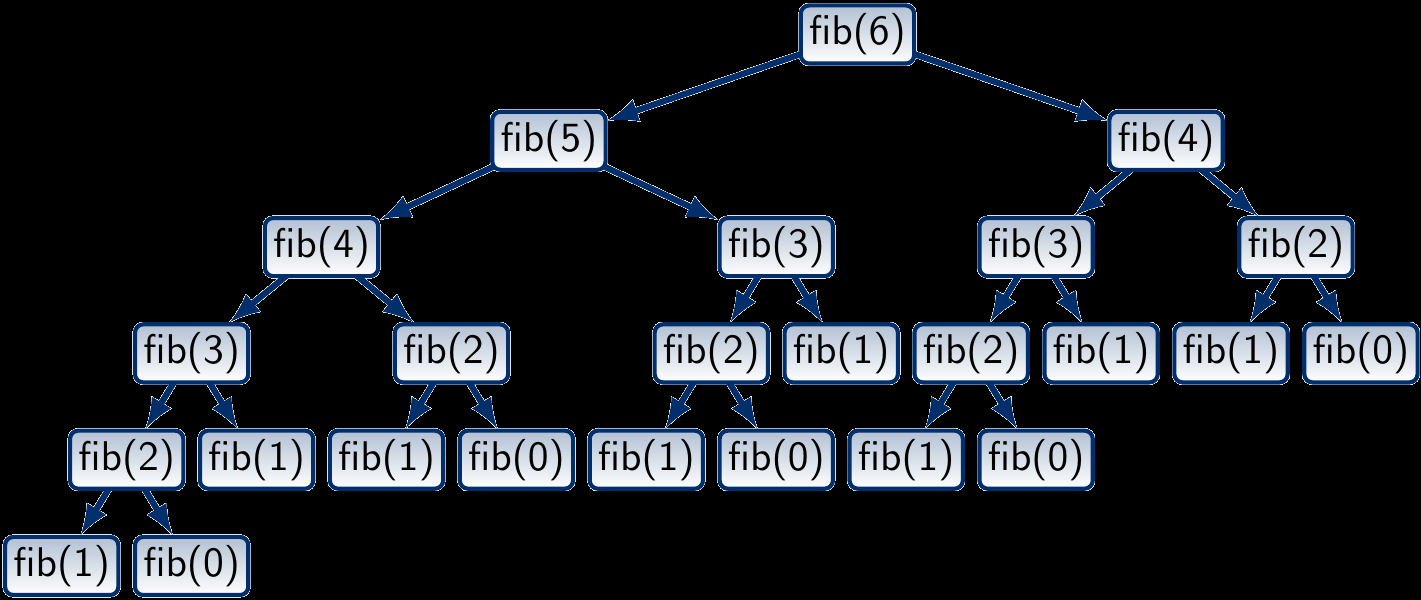
示意圖
#include <iostream>
using namespace std;
long long f(int n){
if(n == 1) return 1;
else if(n == 2) return 2;
return f(n-1) + f(n-2);
}
int main(){
int n;
cin >> n;
cout << f(n) << '\n';
return 0;
}# PRESENTING CODE
Code
可以,但是很慢,複雜度是O(2^n)
如果把算過的記下來,那就不用重複算,
也就是以空間換取時間
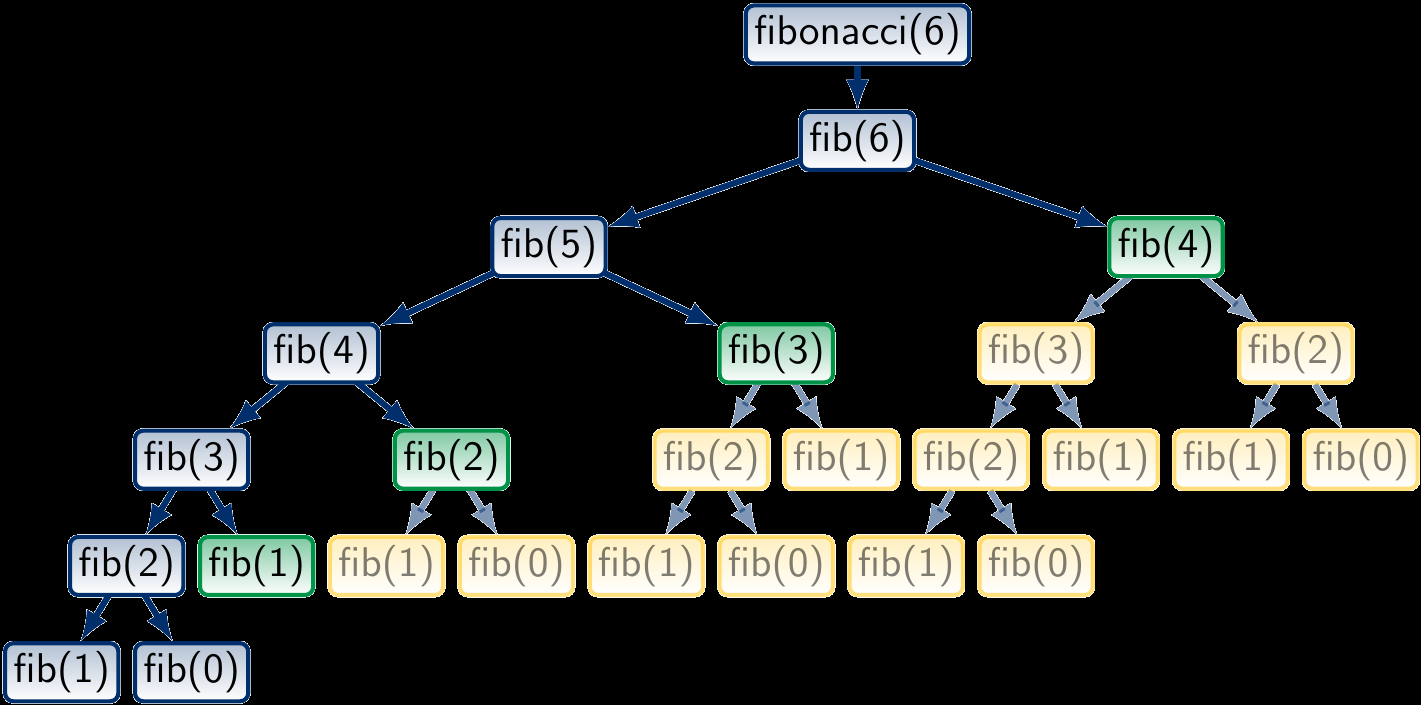
示意圖
# PRESENTING CODE
Bottom up
#include <iostream>
using namespace std;
const int MAXN = 1e6+5
long long dp[MAXN];
long long f(int n){
if(dp[n]) return dp[n];
if(n <= 2) return dp[n] = n;
return dp[n] = f(n-1) + f(n-2);
}
int main(){
int n;
cin >> n;
cout << f(n) << '\n';
}#include <iostream>
using namespace std;
const int MAXN = 1e6+5
long long dp[MAXN];
int main(){
int n;
cin >> n;
dp[1] = 1;
dp[2] = 2;
for(int i=3; i<=n; ++i)
dp[i] = dp[i-1] + dp[i-2];
cout << dp[n] << '\n';
}Top down
使用迴圈
從邊界出發
由下到上計算
使用遞迴
由上到下計算
Bottom up
Top down
DP的特性
- 將大問題切割成多個小問題,再將小問題的解答組合起來
- 最佳子結構:最佳解可以從子問題的最佳解推算
- 重疊子問題:子問題重複計算
- 無後效性:子問題的解確定後不會再被影響
步驟
- 定義狀態
- 推轉移式/遞迴式
- 打邊界
- 實現
實作
2
3 4
6 5 7
4 1 8 3# PRESENTING CODE
定義狀態
若在(i, j),
則必定經過(i-1, j)
或(i-1, j-1)
推轉移式
dp[i][j] = min( dp[ i - 1 ][ j - 1 ], dp[ i - 1 ][ j ] ) + triangle[ i ][ j ]
class Solution {
public:
int minimumTotal(vector<vector<int>>& triangle) {
vector<vector<int>> dp(triangle.size(), vector<int>(triangle.size(), 0)); //走到(i, j)位置上的最小路径和
dp[0][0] = triangle[0][0];
//初始化第一列和最后一列
for(int i = 1; i < triangle.size(); i++){
dp[i][0] = dp[i - 1][0] + triangle[i][0];
dp[i][triangle[i].size() - 1] = dp[i - 1][triangle[i - 1].size() - 1] + triangle[i][triangle[i].size() - 1];
}
for(int i = 1; i < triangle.size(); i++){
for(int j = 1; j < i; j++){
dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j]) + triangle[i][j];
}
}
int res = INT_MAX;
for(int i = 0; i < triangle[triangle.size() - 1].size(); i++){
res = min(res, dp[triangle.size() - 1][i]);
}
return res;
}
};# PRESENTING CODE
Code
參考資料
Code
By ivanlo
Code
- 177



