🌲 Drawing Trees 🌴
using recursion

Prior Knowledge
To access the content of this lesson, you should be comfortable defining and calling a Python function, as well as understanding the difference between parameters and arguments.
Additionally, you need to have a solid grasp of the following functions from the Python turtle module:
- goto(x, y)
- forward(n)
- setheading(angle)
- penup() and pendown()
Look at the code to your right and try to guess the shape that would get drawn.
▶️ to run
✏️ to view the code
Learning Objectives
1. Step by step, code a recursive function that draws a simple tree.
2. Give a formal definition of recursion.
3. Introduce randomness to give the tree a more natural appearance.


1. Drawing a simple tree
Let's break down the problem of drawing a tree into its most essential part. What might this be?
A. drawing the trunk
B. drawing a branch
C. drawing the outline

B. drawing a branch
We can consider the trunk a special and important type of branch, while drawing the outline of a tree doesn't really break down the problem does it?
draw_branch()
▶️ to run
✏️ to view the code
draw_branch() accepts the following parameters:
- x, y as starting coordinates
- angle, length and width of the branch.
And draws the branch for us.
Practice running the code and viewing the source before you complete the tasks.
Draw the practice branches always from bottom to top.
Reveal tasks
Reveal solutionReveal solutionTask 1: Modify the code to draw
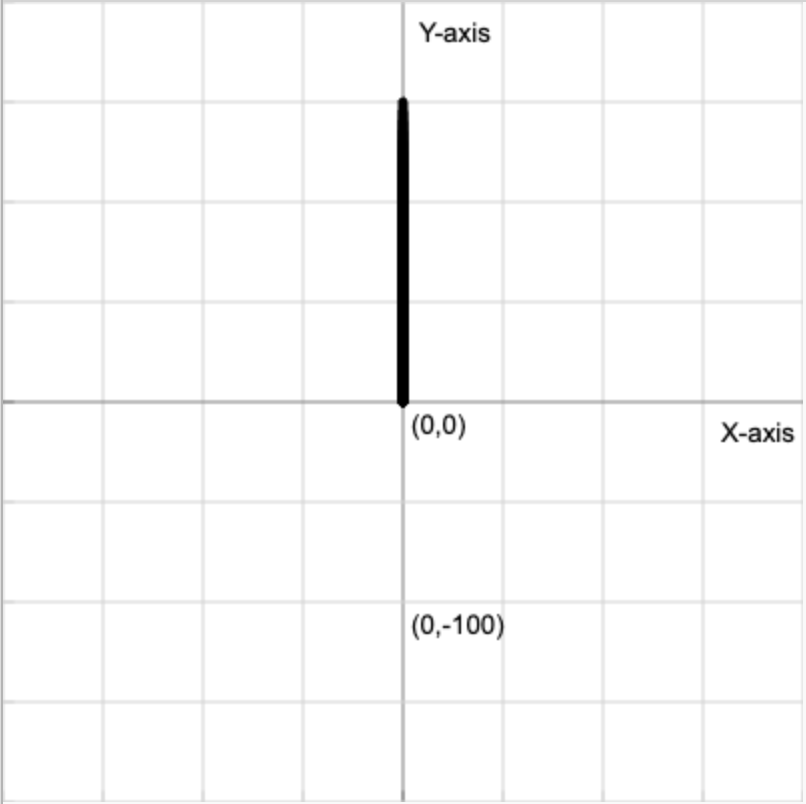
draw_branch(0, 0, 90, 150, 5)Task 2: Modify the code to draw
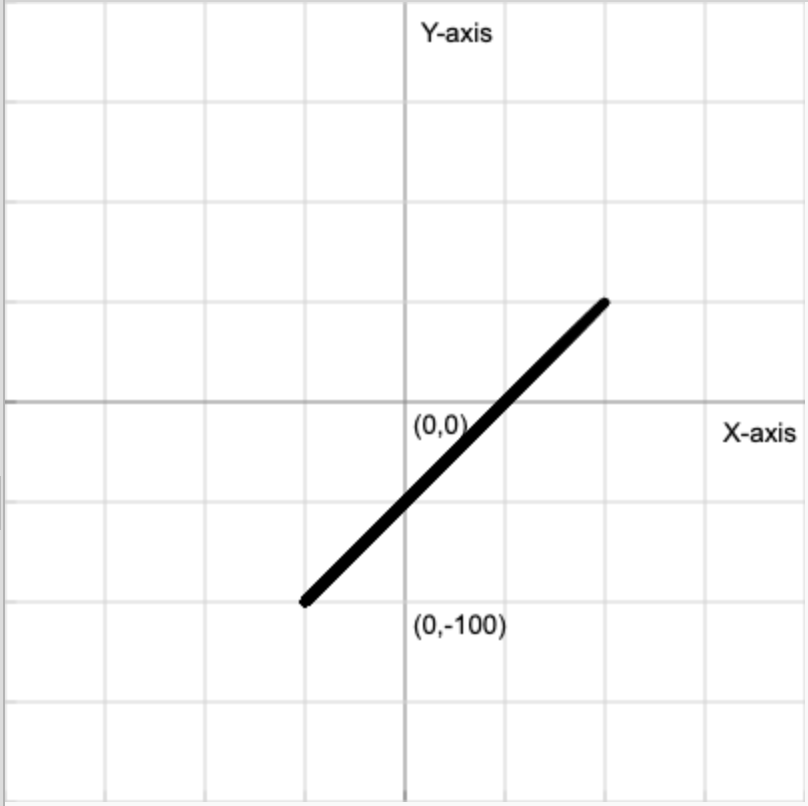
draw_branch(-50, -100, 45, 212, 5)Adding two more branches
The below diagram might help you so keep it in mind.
Task 1:
Call the draw_branch() function two more times, knowing the length should be 75% of the previous branch (trunk), and the width 1px less.
Task 2:
Add these lines to the end of the draw_branch() function, which of these coordinates are shown?
- (53.03, -53.03)
- (56.88, 56.88)
- (-53.03, 53.03)
- (-56.88, 56.88)
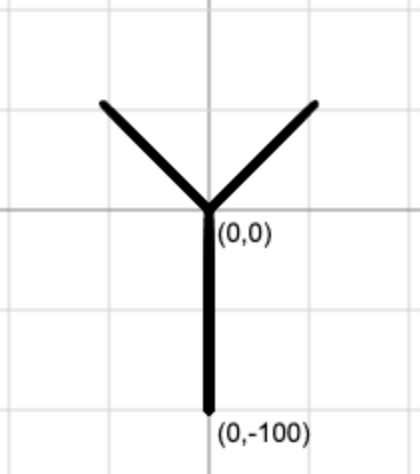
135°
45°
90°
draw_branch(0, 0, 135, 75, 4)
draw_branch(0, 0, 45, 75, 4)end_x, end_y = t.pos()
print(end_x, end_y)Reveal solution❌
❌
✅
❌
Reveal solutionThe recursive step
Let's move the two draw_branch() function calls we wrote inside the draw_branch() function definition.
We'll use end_x and end_y as the starting coordinate and dynamically calculate new length, width and angle (left and right) values based on the previous values (parameters):
- left angle: angle + 45º
- right angle: angle - 45º
- new length: 75% of length
- new width: width - 1px
Task 1:
Uncomment the lines of the recursive step and complete them.
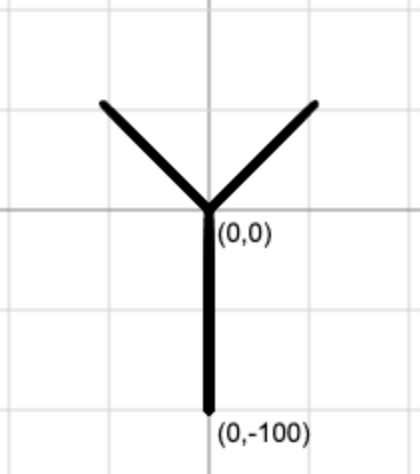
135°
45°
90°
new_length = length * 0.75
new_angle_left = angle + 45
new_angle_right = angle - 45
new_width = width - 1
draw_branch(end_x, end_y, new_length, new_angle_left, new_width)
draw_branch(end_x, end_y, new_length, new_angle_left, new_width)Reveal solutionWhich branch gets drawn for you?
left / right
No wrong answer here! Depending on which angle you chose to draw the first of the two next branches with, you are stuck in a recursive loop. More on that soon!
😱 Stuck in a recursive loop?
Let's pause and read our first formal definition of recursion:
a problem-solving technique where a function calls itself to break down a complex problem into smaller, similar subproblems.
def draw_branch(x, y, angle, length, width):
t = turtle.Turtle()
# Draw branch (hidden)
# Recursive step
end_x, end_y = t.pos()
new_length = length * 0.75
new_angle_left = angle + 45
new_angle_right = angle - 45
new_width = width - 1
draw_branch(end_x, end_y, new_angle_left, new_length, new_width)
draw_branch(end_x, end_y, new_angle_right, new_length, new_width)It should become clear now that we are trying to solve our tree drawing problem using a recursive branch drawing function which calls itself to draw smaller, similar branches every time.
The only issue, is that we are stuck in a recursive loop. Let's see why that is by calling our function and tracing code execution!
draw_branch(0,-100,90,100,5)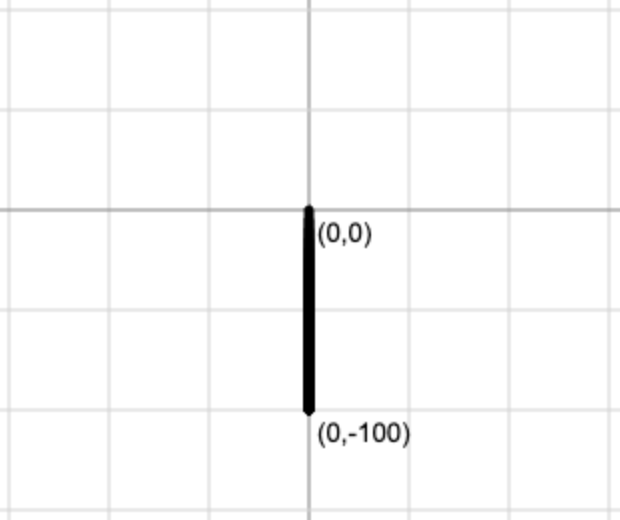
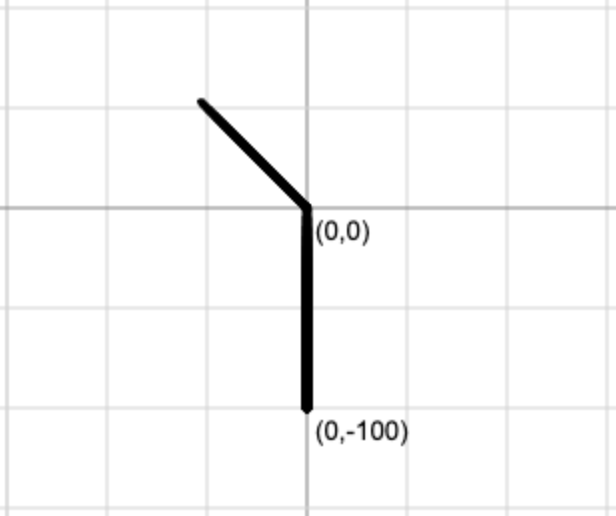
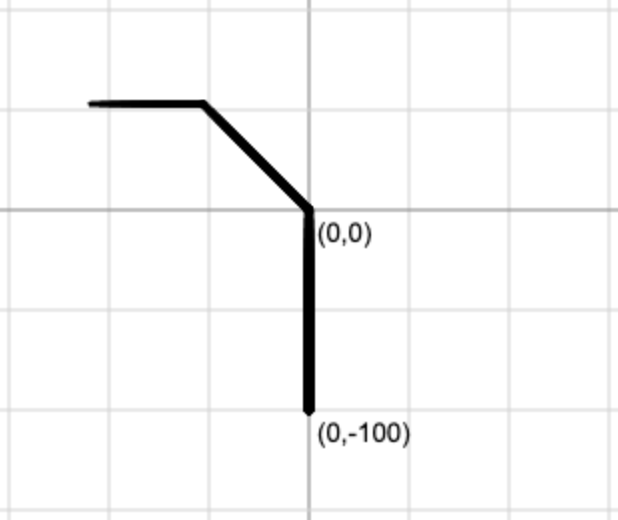
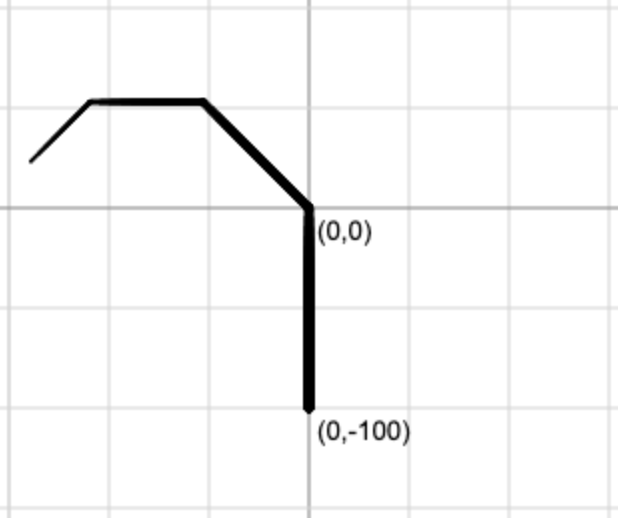
We will never be able to draw any right branches... unless?
The base case
To escape this recursive loop trap, we need to figure out a base case:
When do we stop? When does it no longer make any sense for a branch to be drawn, and for two other branches to spawn from it?
Try these conditions out in the code, which ones work? Which one works best? (click to reveal the answer)
- length is less than 50px
- angle greater than 270º
- y coordinate is less than 0
- width is 0 or less
for faster drawing, we have set the speed of the turtle to the highest value by adding:
t.speed("fastest")✅
❌
❌
👑
Task 1:
Using the width <= 0 condition for the base case, try to make a tree similar to the below screenshot.
def draw_branch(...):
# angle values
angle_left = angle + 30
angle_right = angle - 30
def main():
# starting values
draw_branch(0, -200, 90, 100, 7)Reveal solution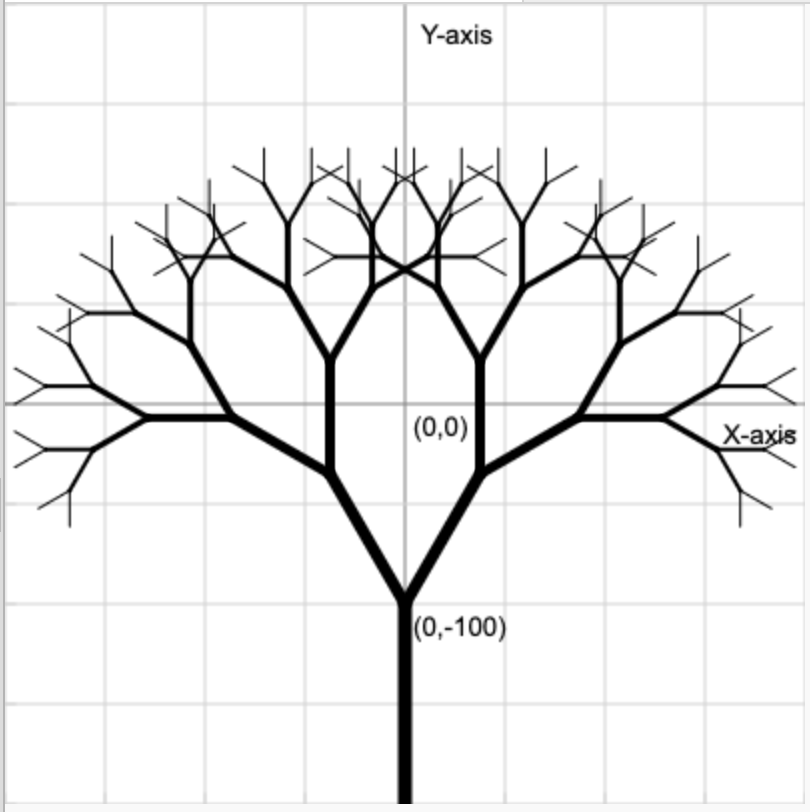
"Recursion is a problem-solving technique where a function calls itself (the recursive step) to break down a complex problem into smaller, similar subproblems. It continues this process until it reaches a base case, a terminal condition that provides a direct answer, allowing the nested solutions to combine and resolve back up the call stack."
function(problem)
function(smaller problem)
function(even smaller problem)
function(base case problem)
we can solve this step directly, no need to go any further!
Formal definition of recursion
We can now make our way back up the call stack, to the first call of the function, solving the entire problem.
Adding randomness
Randomness has been introduced in the angle values of the left and right branches. Run the code to test this out and guess what values in the randint() function might generate a tree like the one the screenshot below.
randint(18,20)
randint(0,50)
randint(80,90)
randint(0,20)❌
❌
❌
✅
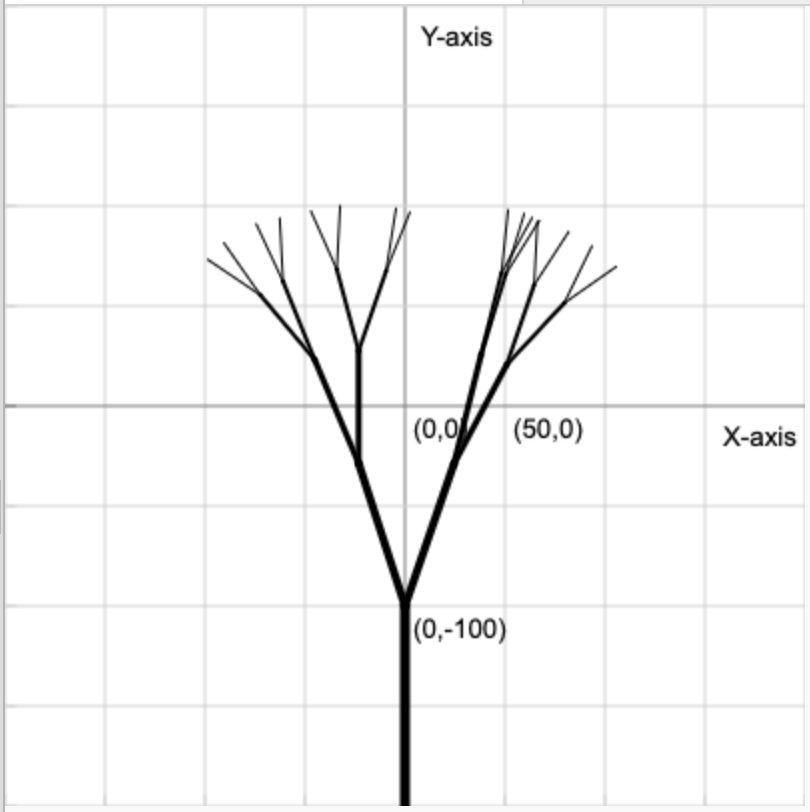

Task 1:
Add randomness to the branch length, so that the next branches are between 75% and 95% of the previous branch... Then change the starting width to 8 and the starting length to 50.
Below and example of what I got.
Reveal solution
def draw_branch(...):
# length
new_length = length * randint(75, 90) / 100
def main():
# starting values
draw_branch(0, -200, 90, 50, 8)Screenshot and feedback!
The code on the right is the same as the one in the previous slide.
Final Task
Modify the random values to create your own personal tree and submit a screenshot of your favourite result below! (You could even try adding colour, remember that the leaves could be those branches with a width of 1)
Recursive Trees
By Jakob Stanley Warth
Recursive Trees
Learn recursion by drawing trees with python's turtle library
- 88


