14c Exponential Modelling
14c Exponential Modelling
\(e^x\) is used to model situations like population growth, where the rate of growth is proportional to the size of the population at any given time.
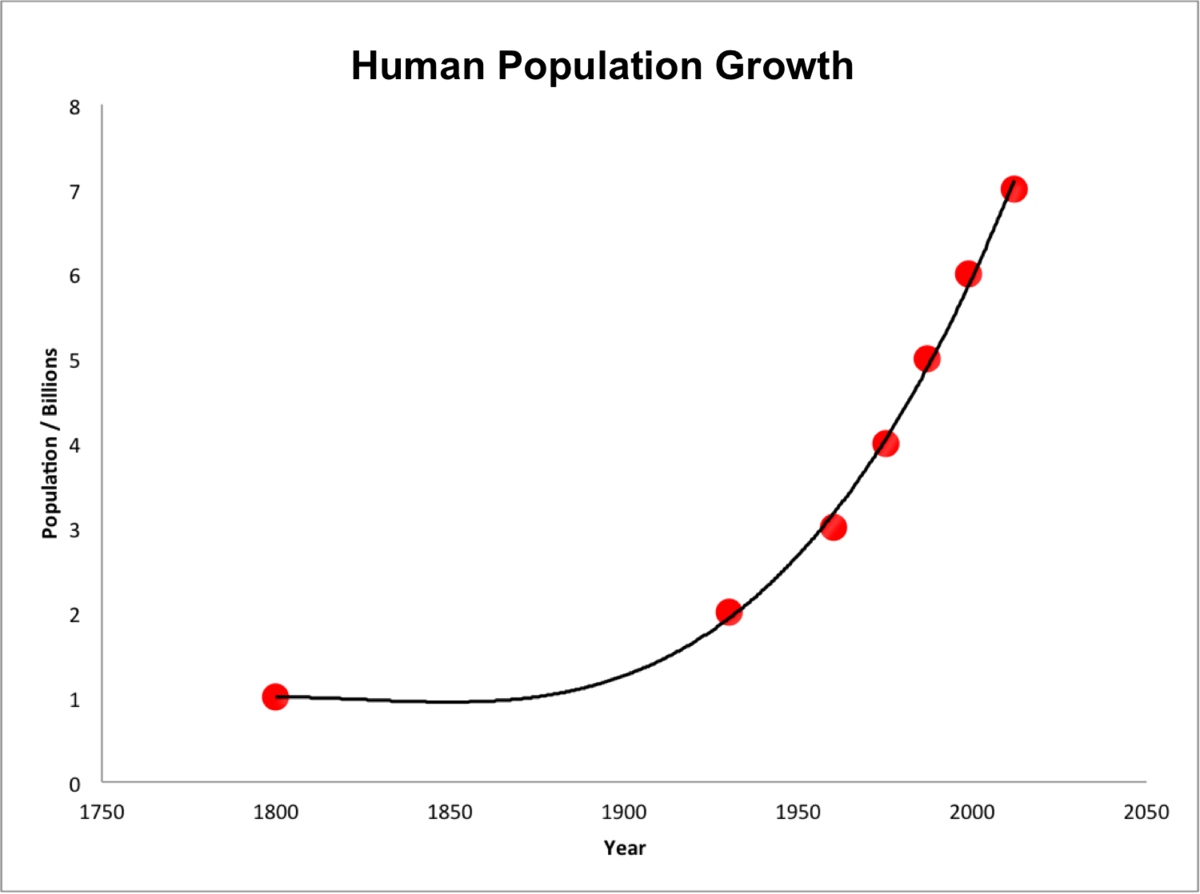
14c Exponential Modelling
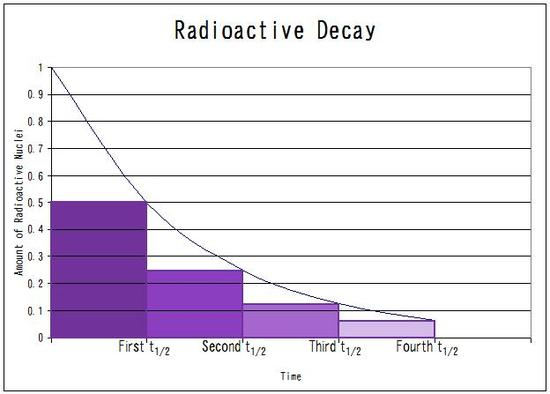
\(e^{-x}\) is used to model situations like radioactive decay, where the rate of decrease is proportional to the number of atoms remaining.
Example
The density of a pesticide in given section of field, P mg/m², can be modelled by the equation:
\[P = 160e^{-0.006t}\]
where \(t\) is the time in days since the pesticide was first applied.
- Use this model to estimate the density of the pesticide after 15 days.
- Interpret the meaning of the value 160 in this model.
- Show that \(\frac{dP}{dt} = kP\), where \(k\) is a constant, and state the value of \(k\).
- Interpret the significance of the sign of your answer to part 3.
- Sketch the graph of \(P\) against \(t\).
Example
The density of a pesticide in given section of field, P mg/m², can be modelled by the equation:
\[P = 160e^{-0.006t}\]
where \(t\) is the time in days since the pesticide was first applied.
- Use this model to estimate the density of the pesticide after 15 days.
\[P = 160 \times e^{-0.006\times15}\]
\[P = 142.22\ldots\]
\(P = 142\) mg/m²
Example
The density of a pesticide in given section of field, P mg/m², can be modelled by the equation:
\[P = 160e^{-0.006t}\]
where \(t\) is the time in days since the pesticide was first applied.
- Interpret the meaning of the value 160 in this model.
It is the maximum value for \(P\), when \(t = 0\), so it is the initial density of pesticide.
Example
The density of a pesticide in given section of field, P mg/m², can be modelled by the equation:
\[P = 160e^{-0.006t}\]
where \(t\) is the time in days since the pesticide was first applied.
- Show that \(\frac{dP}{dt} = kP\), where \(k\) is a constant, and state the value of \(k\).
\[P = 160e^{-0.006t}\]
\[\frac{dP}{dt} = -0.006\times160e^{-0.006t}\]
\[\frac{dP}{dt} = -0.96e^{-0.006t}\]
\[k = -0.96\]
Example
The density of a pesticide in given section of field, P mg/m², can be modelled by the equation:
\[P = 160e^{-0.006t}\]
where \(t\) is the time in days since the pesticide was first applied.
- Interpret the significance of the sign of your answer to part 3.
\(k = -0.96\), so the rate of change of density is decreasing (there is exponential decay).
Example
The density of a pesticide in given section of field, P mg/m², can be modelled by the equation:
\[P = 160e^{-0.006t}\]
where \(t\) is the time in days since the pesticide was first applied.
- Sketch the graph of \(P\) against \(t\).
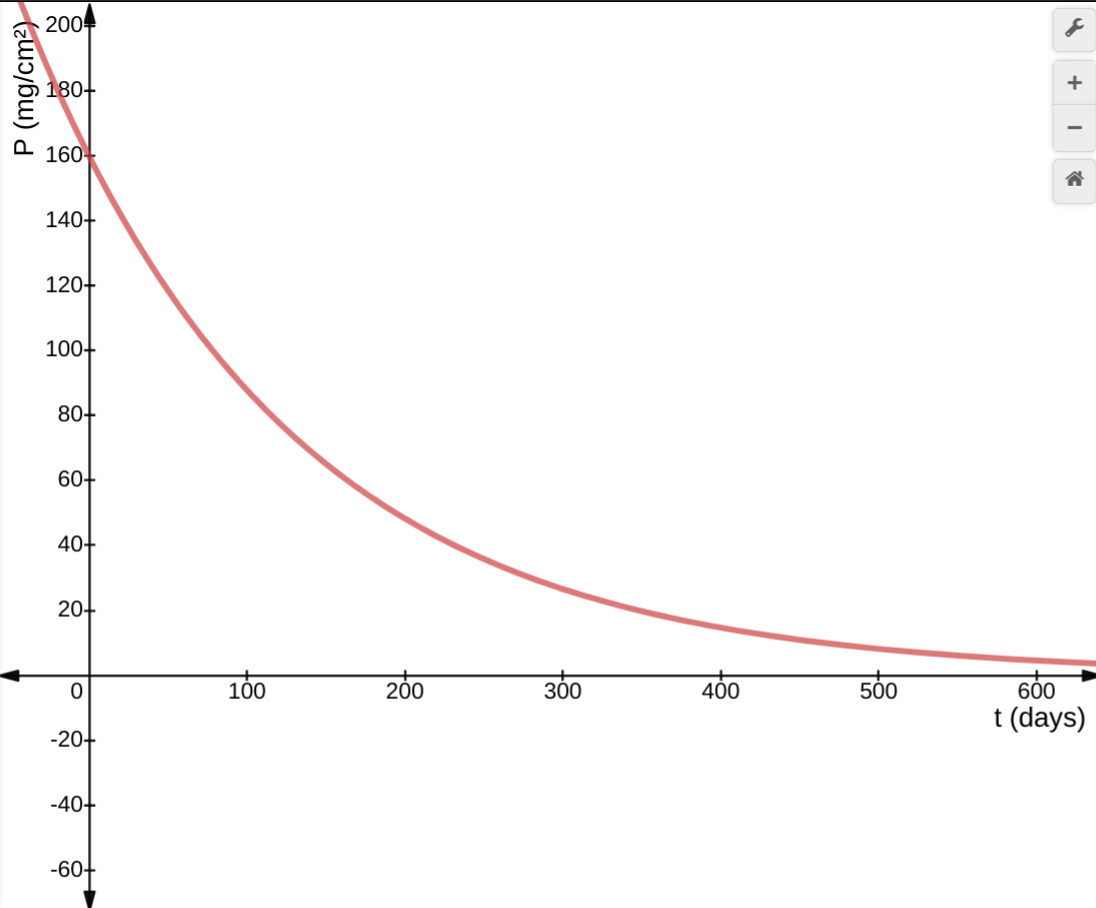
You know from part 2, that the y-intercept is 160 and you know from part 4, that it is an exponential decay.
14c Exponential Modelling
By David James
14c Exponential Modelling
- 361



