3f Representing Images
3f Representing Images
- Understand what a pixel is and be able to describe how pixels relate to an image and the way images are displayed.
- Describe the following for bitmaps: image size; colour depth.
- Know that the size of a bitmap image is measured in pixels (width × height).
- Describe how a bitmap represents an image using pixels and colour depth.
- Describe using examples how the number of pixels and colour depth can affect the file size of a bitmap image.
- Calculate bitmap image file sizes based on the number of pixels and colour depth.
- Convert binary data into a bitmap image.
- Convert a bitmap image into binary data.
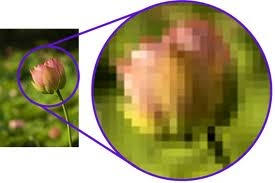
The Pixel
A bitmap image is made up of lots of picture elements (pixels).

Each pixel is a small rectangular block that has information about its colour.
Width = 13 pixels
Height = 11 pixels
Colours = 3 (red, white, black)
Resolution
Image resolution is the number pixels in the image.

Width = 13 pixels
Height = 11 pixels
Number of pixels = 13 × 11 = 143
Resolution

The higher the resolution, more pixels in an image, the more detail can be displayed, making the image more realistic.

Colour Depth
Each pixel has a colour depth.

The number of colours that can be displayed.
1 bit colour depth = 21 = 2 colours
2 bit colour depth = 22 = 4 colours
3 bit colour depth = 23 = 8 colours
8 bit colour depth = 28 = 256 colours
16 bit colour depth = 216 = 65,536 colours
24 bit colour depth = 224 = 16,777,216 colours
True colour (humans can distinguish approximately 10,000,000 colours)
2 bit colour depth
Colour Depth
The greater the colour depth, the more colours can be displayed, allowing more realistic images.


Image Size
An image's size is calculated from the number of pixels multiplied by the colour depth.

Width = 13 pixels
Height = 11 pixels
Colours = 3 (red, white, black)
Number of pixels = 143
Colour depth = 2 (four colour)
Image size
143 × 2 = 286 bits
286 ÷ 8 = 35.75 (36 bytes)
My First Monitor
My first monitor had a resolution of 640 × 480 with 16 bit colour.
So each image on the screen was:
640 × 480 × 16 = 4,915,200 bits
4,915,200 ÷ 8 = 614,400 bytes
approximately 614 kB

Modern Monitors

approximately 6.9 MB
This presentation was created on a monitor with a resolution of 1920 × 1200 and the colour depth is 24 bit.
So each image on the screen is:
1920 × 1200 × 24 = 55,296,000 bits
55,296,000 ÷ 8 = 6,912,000 bytes
Convert an Image to Binary
Each pixel has the binary color assigned to it.
Two colours means one bit.
Let white be '0' and blue be '1'.
1
1
1
1
1
0
0
0
0
1
0
1
0
1
0
1
0
1
Convert Binary Data to an Image
This binary value represents an image of resolution 5 x 5 with a colour depth of 2.
0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0
Draw the image, use the grid to help you.
Work from left to right putting the binary number in each square.
Shade in the squares that contain a '1'.
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
1
Questions
- Convert the image into binary where white is given the value '1' and black is given the value '0'.
- What is colour depth?
- Calculate how many different colours a 5-bit image can use.
- What is the formula that relates file size, image resolution and colour depth?
- Give one advantage and one disadvantage of using images with a high resolution.
- An image is 10 pixels high, 10 pixels wide and has a colour depth of 4 bits. What is the file size (in bits) of the image?
- An image with only two colours is saved as a 4-bit image. Explain why this is inefficient.
Questions
- What is colour depth?
The number of bits used for each pixel.
- Calculate how many different colours a 5-bit image can use.
2⁵ = 2 × 2 × 2 × 2 × 2 = 32
- What is the formula that relates file size, image resolution and colour depth?
file size (bits) = width × height × colour depth
- Give one advantage and one disadvantage of using images with a high resolution.
Advantage: likely to produce a better quality image
Disadvantage: will require more storage space
Questions
- What is the formula that relates file size, image resolution and colour depth?
file size (bits) = width × height × colour depth
- Give one advantage and one disadvantage of using images with a high resolution.
Advantage: likely to produce a better quality image
Disadvantage: will require more storage space
- An image is 10 pixels high, 10 pixels wide and has a colour depth of 4 bits. What is the file size (in bits) of the image?
10 × 10 × 4 = 400 bits
Questions
- An image with only two colours is saved as a 4-bit image. Explain why this is inefficient.
- Give one advantage and one disadvantage of using images with a high resolution.
Advantage: likely to produce a better quality image
Disadvantage: will require more storage space
- An image is 10 pixels high, 10 pixels wide and has a colour depth of 4 bits. What is the file size (in bits) of the image?
10 × 10 × 4 = 400 bits
Two colours only needs 1 bit colour depth, so a 4-bit image will need four times the storage it needs.
Questions
- An image is 10 pixels high, 10 pixels wide and has a colour depth of 4 bits. What is the file size (in bits) of the image?
10 × 10 × 4 = 400 bits
- An image with only two colours is saved as a 4-bit image. Explain why this is inefficient.
Two colours only needs 1 bit colour depth, so a 4-bit image will need four times the storage it needs.
1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1
- Convert the image into binary where white is given the value '1' and black is given the value '0'.
3f Representing Images
- Understand what a pixel is and be able to describe how pixels relate to an image and the way images are displayed.
- Describe the following for bitmaps: image size; colour depth.
- Know that the size of a bitmap image is measured in pixels (width × height).
- Describe how a bitmap represents an image using pixels and colour depth.
- Describe using examples how the number of pixels and colour depth can affect the file size of a bitmap image.
- Calculate bitmap image file sizes based on the number of pixels and colour depth.
- Convert binary data into a bitmap image.
- Convert a bitmap image into binary data.
3f Representing Images
By David James
3f Representing Images
Computer Science - Fundamentals of Data Representation - Representing Images
- 659



