Categories

Characterize

Characteristic Conditions

 

— by Five Guys (BDMOW)

https://slides.com/jameswilson-3/characteristic/

https://arxiv.org/abs/2502.01138

  • 1545 Tartaglia  and Cardano face off in a duel:
    • each chooses 30 polynomials (nerds!)
    • the winner factors the most
  • Why can they compete?
    • Because you don't need to know the method to certify the solution, e.g. multiply \[x^3-1=\begin{array}{|c|ccc|} \hline & x^2 & +x & +1\\ \hline x & x^3 & x^2 & x \\ -1 & -x^2 & -x & -1\\ \hline \end{array}\]
  • Who won?
    • The two men tore up each others solutions and insulted one-another.

An Historic Competition

  • 2018+ Five guys face:
    • billions of groups
    • They keep their grants if they find characteristic subgroups to constrain automorphisms
  • Ada Rottländer 1928, primes \(p,q\) and constants \(a,b\in \mathbb{Z}/_q\) \[G=\left\{\begin{bmatrix} a^{e} & . & u\\ . & b^e  & v \\ . & . &  1\end{bmatrix}~\middle|~\begin{array}{c} e\in\mathbb{Z}/p,\\u,v\in \mathbb{Z}/q\end{array}\right\}\]
  • Sometimes these are characteristic subgroups \[C_1=\left\{\begin{bmatrix} 1 & . & *\\ . & 1  & . \\ . & . &  1\end{bmatrix}\right\}\qquad C_2=\left\{\begin{bmatrix} 1  & . & .\\ . & 1   & *  \\ . & . &  1\end{bmatrix}\right\}\]When? Some stupid number theory.
    How to confirm? Compute automorphisms (defeats the purpose).

A Modern Competition

\((\mathbb{Z}/q)^n\rtimes \mathbb{Z}/p\)

\[G=\left\{\begin{bmatrix} \ddots  & & & \vdots \\  &  a_i^e & & u_i\\  & & \ddots & \vdots \\ & & & 1 \end{bmatrix}~\middle|~\begin{array}{c} e\in\mathbb{Z}/p,\\u_i\in \mathbb{Z}/q\end{array}\right\}\]

Some of these are characteristic, do you know which ones? Could you know without computing \(\text{Aut}(G)\)? \[C_i=\left\{\begin{bmatrix} \ddots &  & & 0\\  & 1  &  & * \\  &  &  \ddots & 0 \\ & & & 1\end{bmatrix}\right\}\]

This is what happens for the dumbest groups, for "grant-grade groups" it's ... bananas!

Building automorphism groups

Initialize

1 Ad hoc Char

Organize

2 Filters & Sediments

Lie theory

3 Derive

Orbit-stab.

4 Prune

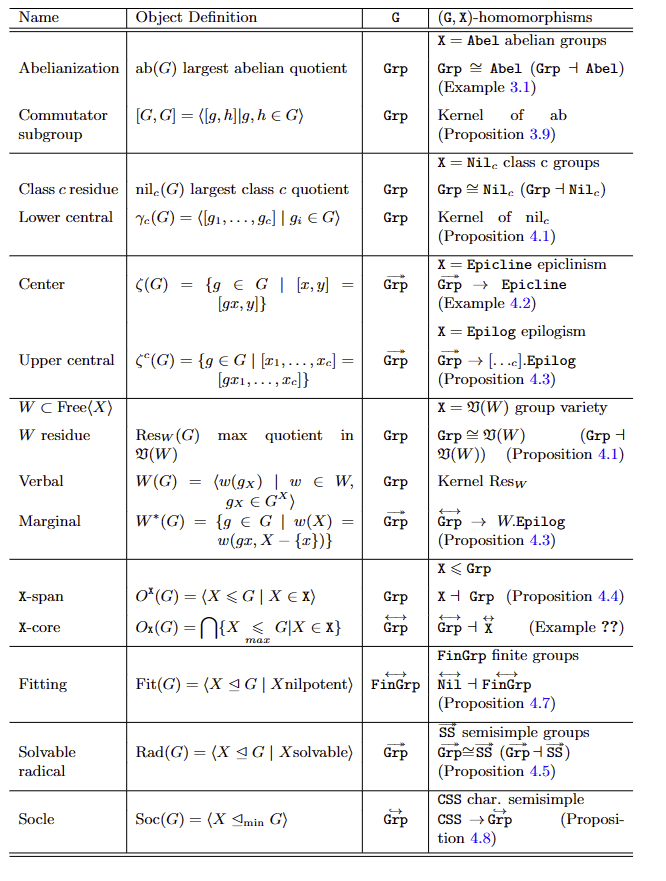
Type 1 Named

  • Cayley, Holder (center, commutator, powers)
  • Fitting (cores, Fitting subgroup, solvable radical)
  • Hall (Verbal, Marginal)
  • Thompson, Glauberman, Alperin, them, you, us, ... 

1 Ad hoc Char. Search

Type 2 Hunted

  • Eick, Leedham-Green, O'Brien 02
  • Cannon, Holt 03
  • Eick 04

Type 3 Derived

  • Wilson 12, 15
  • Maglione 15,17, 21
  • Brooksbank-O'Brien-W. 19
  • \(\langle M,+,0,\prec \rangle\) pre-ordered commutative monoid.
  • (Char) Filter: \(\phi:M\to \text{Sub}(G)\) where \[\forall s\forall t. [\phi_s,\phi_t] \leq \phi_{s+t}\quad\wedge\quad s\prec t \Rightarrow \phi_s\geq \phi_t\]
  • Boundry Filter: \(\displaystyle \partial_s \phi := \langle \phi_{s+t}\mid 0\prec t\rangle\)

2 Filters & Sediments

Sediments: "upper" version, \([\phi^s,\pi^{s+t}]\leq \pi^t\), makes an \(L_*\)-Lie comodule \(\bigoplus_{0\prec s} \partial^s\pi/\pi^s\).

Thm (W. 12).  \(\mathcal{H}\subset \text{Sub}(G)\) generates a unique filter containing* \(\mathcal{H}\).

Thm (W. 12).  Get a graded Lie \(\mathbb{Z}[\phi_0/\partial_0\phi]\)-algebra \(\displaystyle L_*(\phi)=\bigoplus_{0\prec s} \phi_s/\partial_s\phi\)

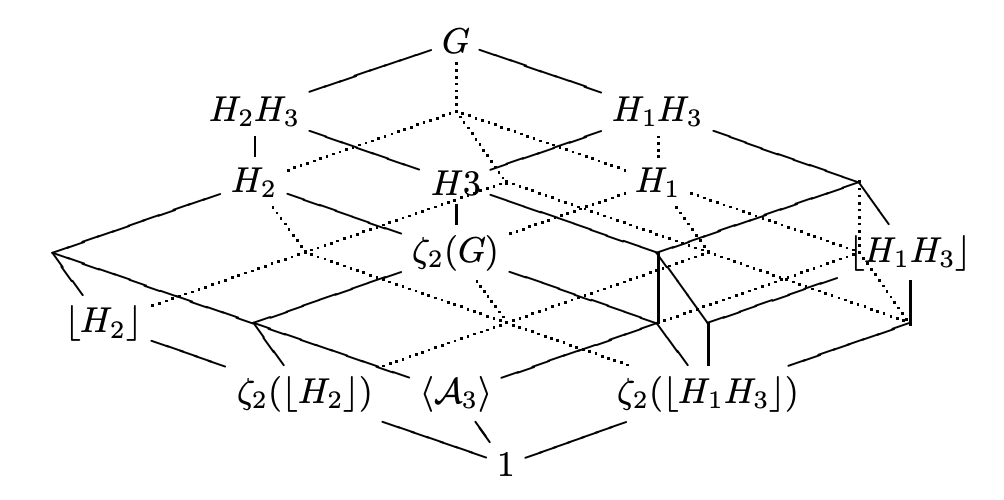
Generating \(\phi:\mathbb{N}^3/_{\sim} \to \text{Sub}(G)\)

*Needs a generalized refinement monoid; see Dobbertin 82

3 Lifting Filters

Sediments: "upper" version on comodule.

Thm (W. 15).  If \(\phi:M\to \mathsf{Char}(G)\) then \[\alpha_s = \{ f\in \text{Aut}(G)\mid \forall t\forall x\in \phi_t\; f(x)x^{-1}\in \phi_{s+t}\}\] is a filter of \(\text{Aut}(G)\) and

\[L_*(\alpha) \hookrightarrow \text{Der}(L_*(\phi)).\]

Note: \(\text{Der}(L_*(\phi))\) is efficiently computable.

Linearizes aspects of the desired group \(\text{Aut}(G)\).

\begin{array}{|ccccc|} \hline f_{00} & & & & \\ & f_{11} & & & \\ & & f_{22} & & \\ & & & \ddots & \\ & & & & \ddots\\ \hline \end{array}

\(\phi:\mathbb{N}\to \text{Char}(G)\), \(L_i=\phi_i/\partial_i\phi\)

\(f\in \alpha_0:=\text{Aut}(G)\)  

\begin{array}{|c|} \hline L_0\\ L_1\\ L_2\\ \vdots\\ \\ \\ \hline \end{array}

\(f \partial_0\alpha\in \alpha_0/\partial_0\alpha\) acts as

on \(L_*(\phi)\)

\(\phi:\mathbb{N}\to \text{Char}(G)\), \(L_i=\phi_i/\partial_i\phi\)

\(f\in\alpha_1\)   

\begin{array}{|c|} \hline L_0\\ L_1\\ L_2\\ \vdots\\ \\ \\ \hline \end{array}
\begin{array}{|ccccc|} \hline 0 & f_{01} & \cdots & & \\ & 0 & f_{12} & \cdots & \\ & & 0 & \ddots & \\ & & & \ddots & \\ & & & & \ddots\\ \hline \end{array}

\([x,f]:L_i\to L_{i+1}\) acts as

on \(L_*(\phi)\)

\(\phi:\mathbb{N}\to \text{Char}(G)\), \(L_i=\phi_i/\partial_i\phi\)

\(f\in\alpha_2\)   

\begin{array}{|c|} \hline L_0\\ L_1\\ L_2\\ \vdots\\ \\ \\ \hline \end{array}
\begin{array}{|ccccc|} \hline 0 & 0 & f_{02} & \cdots & \\ & 0 & 0 & f_{13} & \cdots \\ & & 0 & 0 & \\ & & & \ddots \\ & & & & \ddots\\ \hline \end{array}

\([x,f]:L_i\to L_{i+2}\) acts as

on \(L_*(\phi)\)

4 Prune to \(\text{Aut}(G)\)

Thm (Brooksbank-W. 12) + Thm (Ivanyos-Qiao 14) lets us lift back to \(\text{Aut}(G)\) throwing out what does not lift.

 

Building automorphism groups with imposter characteristic

Initialize

1 Ad hoc Chars in G

Organize

2 Char Filters of G

Lie theory

3 Derive Der(Lie(Aut(G))

Orbit-stab.

4 Prune to Aut(G)

Interlude

Hausdorff Inst. Math. asked logic & group theory to be friends.

 

James asked google:

"what is logic?"

and got sent to nLab.

 

This is what happened next...

Introducing the

Cyber-Char!

With all the Category Theory of a first time Mushroom Picker,

                                  .... the Type Theory of a Rubber Stamp, &

                                     ... the Model Theory of a Lego Duplo Set.

Cyber-Char

Categorification

Reveal a categorical description of characteristic.

1.

Category algebra

Demonstrate the target data for characteristics is actually found in representation theory of categories.

2.

Computational Categories

Bring it back to applications by creating computable categories.

3.

Thanks

  • DFG grant VO 1248/4-1 & DFG-GRK 2297

  • Marsden Fund of New Zealand UOA 107

  • Simons Foundation #636189

  • USA NSF 2319370

Characteristic

Characteristic

Substructure or partitions that do not change under automorphisms.

1.

Category Actions

Categories acting is more intuitive than groups acting.

2.

Characteristic = biaction homomorphisms.

A complete description of characteristic without involving isomorphisms.

3.

Selfish Characteristic

\(H\leq G\) where for every automorphism \(\varphi:G\to G\), \(\varphi(H)=H\).

Gregarious Characteristic

\(H\leq G\) and \(\varphi,\psi:G\to \tilde{G}\) isomorphisms, then \(\varphi(H)=\psi(H)=:\tilde{H}\).

\begin{array}{lcl} H~~ & \overset{\iota_G}{\hookrightarrow} & G~~\\ \downarrow \varphi|_H & & \downarrow \varphi\\ H~~ & \overset{\iota_G}{\hookrightarrow} & G~~ \end{array}
\begin{array}{lcl} H~~ & \overset{\iota_G}{\hookrightarrow} & G~~\\ \downarrow \varphi|_H & & \downarrow \varphi\\ \tilde{H}~~ & \overset{\iota_{\tilde{G}}}{\hookrightarrow} & \tilde{G}~~ \end{array}

Groups are fond of company, not selfish.

What you can learn on nLab: how to multiply dots-and-arrows.

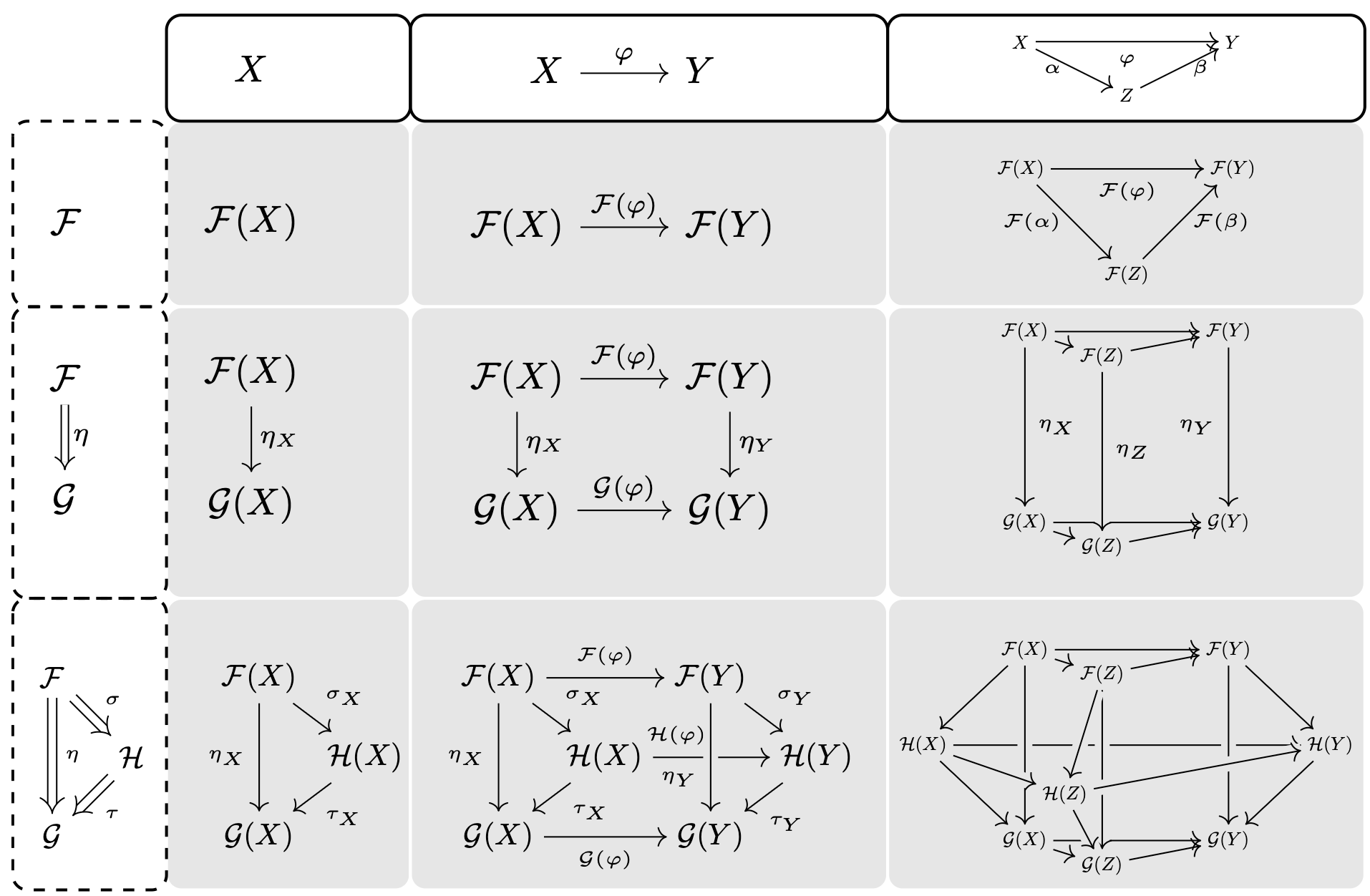
Selfish Characteristic

Gregarious Characteristic

\begin{array}{l|lcl} & C & \overset{\iota}{\Rightarrow} & 1\\ \hline G & C(G)~~ & \overset{\iota_G}{\hookrightarrow} & 1(G)~~\\ \downarrow \varphi& \downarrow C(\varphi) & & \downarrow \varphi\\ G & C(G)~~ & \overset{\iota_G}{\hookrightarrow} & 1(G)~~\\ \end{array}
\begin{array}{l|lcl} & C & \overset{\iota}{\Rightarrow} & 1\\ \hline G & C(G)~~ & \overset{\iota_G}{\hookrightarrow} & 1(G)~~\\ \downarrow \varphi& \downarrow C(\varphi) & & \downarrow \varphi\\ K & C(K)~~ & \overset{\iota_{K}}{\hookrightarrow} & 1(K)~~\\ \end{array}

\(C:\text{Aut}(G)\to \text{Aut}(H)\) is a functor

\(\iota:C\Rightarrow 1\) is a natural transformation.

\(C:\overset{\longleftrightarrow}{\text{Group}}\to \overset{\longleftrightarrow}{\text{Group}}\) is a better functor

\(\iota:C\Rightarrow 1\) is a natural transformation.

Technical glitch: inclussions aren't isomorphisms.

Selfish Characteristic

Gregarious Characteristic

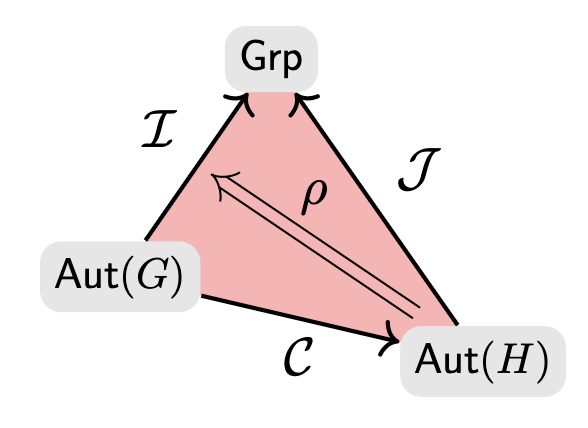
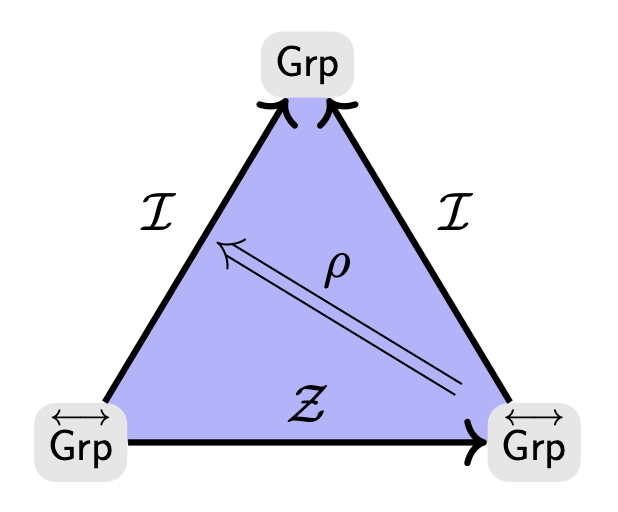
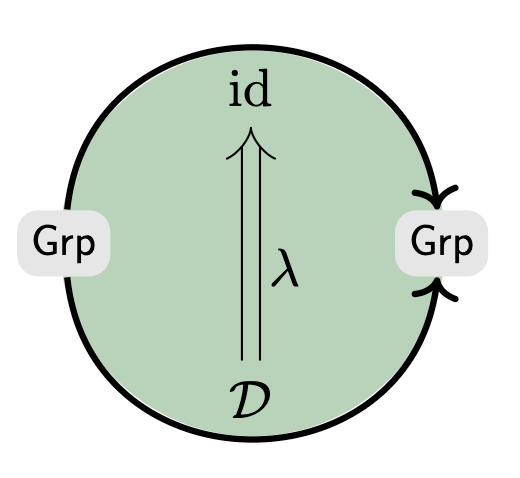
Gregarious Fully Invariant

Thm Five Guys.  All selfish group characteristics can be made gregariuos.

Characteristic

Characteristic

Substructure or partitions that do not change under automorphisms.

1.

Category Actions

Categories acting is more intuitive than groups acting.

2.

Characteristic = biaction homomorphisms.

A complete description of characteristic without involving isomorphisms.

3.

Everyone knows categories have 

  • a class of objects
  • for objects \(X,Y\) a set of morphisms \(\hom(X,Y)\), &
  • associative composition, identities.

Some requirements get over looked:

  • An equality between objects (don't have ZF  Axiom of Extensionality).
  • a notion of class over which we can quantify, alt. consistency of large cardinals and ramification, computability.
  • \(\forall X\forall X'\forall Y\forall Y'.\hom(X,Y)\cap \hom(X',Y')\neq \emptyset\Rightarrow (X=X')\wedge(Y=Y')\)

Abstract Category

\(g(hk)=(gh)k\)

\(\lhd \bot=\bot=\bot\lhd\)

\((\lhd g)g=g\)      \(g(g\lhd)=g\)

\(\bot g=\bot=g\bot\)

\(\bot : A^0\to A\)

\(\lhd(-) : A^1\to A\)

\((-)\lhd : A^1\to A\)

\(\cdot : A^2\to A\)

\(\lhd (fg)=\lhd(f(\lhd g)\)

\((fg)\lhd=((f\lhd)g)\lhd\)

     \(\lhd(g\lhd)=g\lhd\)

     \((\lhd g)\lhd=\lhd g\)

I.e. If you throw away objects (a 2 sorted theory) then categories are just models in an variety of algebraic structures.

Categories as Algebra

Abstract Category

\(g(hk)=(gh)k\)

A associative multiplication with sink and 1s.

\[\begin{array}{|c|ccc|} \hline * & e & h & f\\ \hline e & e & \bot & \bot \\ h & h & \bot & \bot \\ f & \bot & h & f \\ \hline\end{array}\]

\(\bot g=\bot=g\bot\)

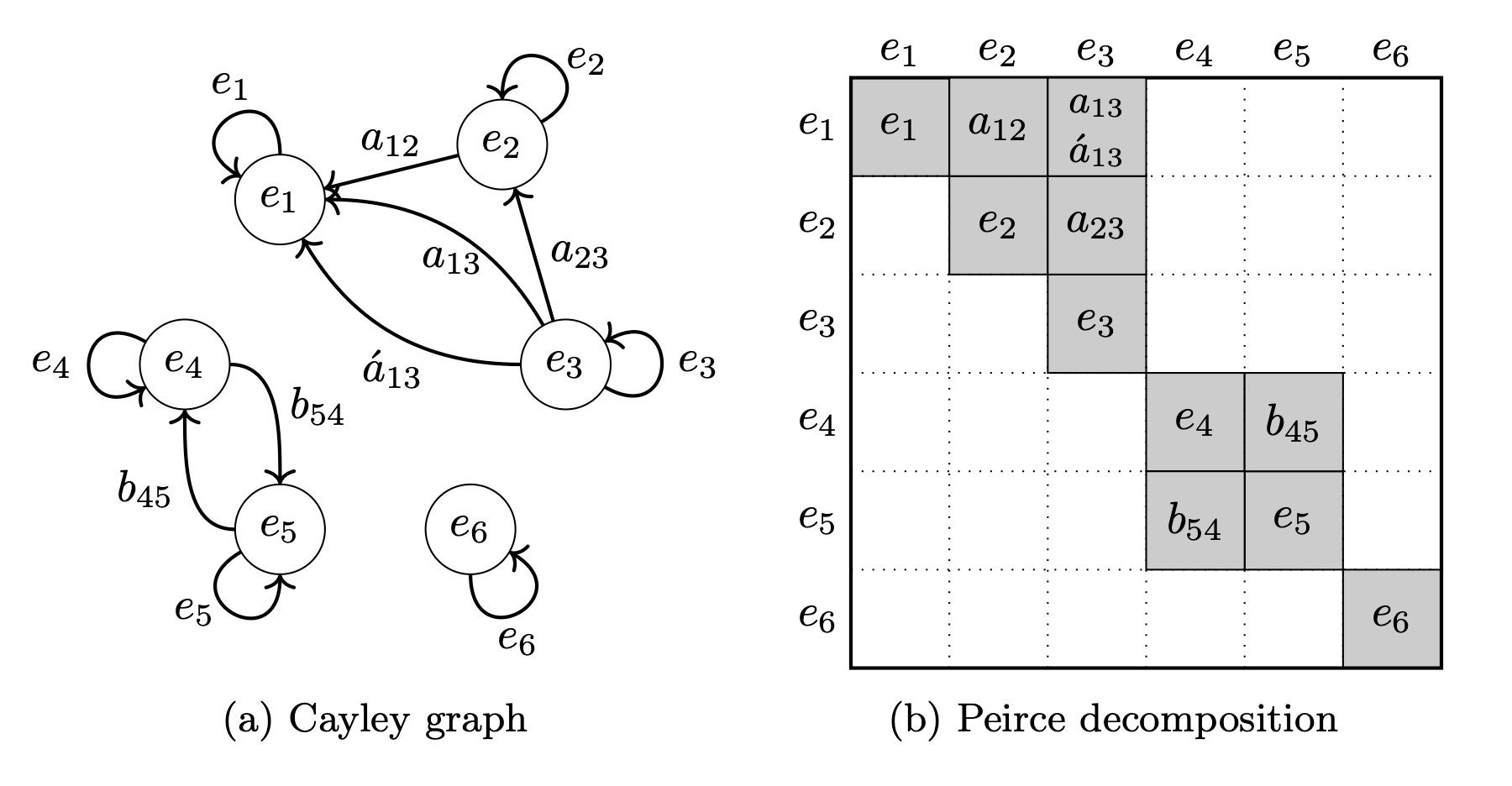
  • Exchange Set Theory for Model Theory
  • Universal algebra definitions & arguments 
  • E.g. Peirce decomp. Noether's Isomorphisms, quotients, images, representations

The result

Hom(X,Y) is \(eAf\) cosets

Category actions

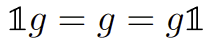
\(\cdot : A\times X\to X\)

\(g(hx)=(gh)x\)

\[\begin{bmatrix}  \{e\} & \bot \\ \{h\} & \{f\} \end{bmatrix} \begin{bmatrix} \{x_1\} \\  \{x_2\}\end{bmatrix} = \begin{bmatrix} \{x_1\}\\ \{x_2\} \end{bmatrix}\]

\(\bot x=\bot=x\bot\)

Category

"capsules"

\(x=x\)

Left, right, bi-capsules as usual.

Category actions on Categories

Assume a few technical nondegeneracy adjectives the following hold

  • Fact.  Category \(A\) acting on \(B\) is the same as functor \(F:A\to B\) [compare rings: \(f:A\to B\) makes \(B\) a left/right \(A\)-module].
  • Fact.  \(A,B\)-actions \(\mathcal{M}:B\to A\) defined by the image of units.
  • Fact.  Adjoint functor pairs are nothing but \(M:B\to A, N:A\to B\) where \[MNM=M\qquad NMN=N\]

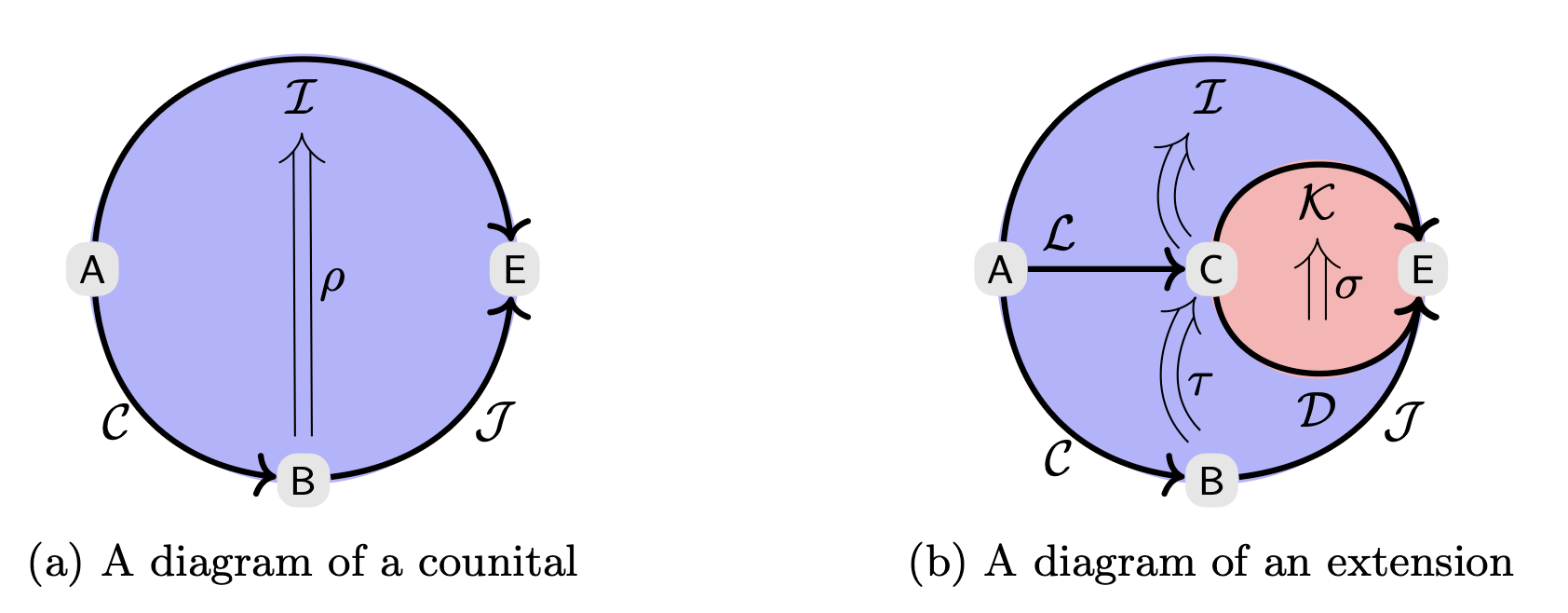
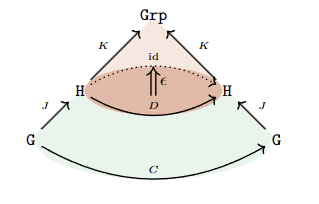
Thm. (Five Guys) In a category A,

\(H\) characteristic in \(G\) if, and only if, \(\exists B\)\(\exists X=A\mu B\) a cyclic \((A,B)\)-capsule with \[C(G)=1_G \cdot \mu\]

Corollary. You can certify characteristic without automorphisms.

Thm'. Characteristic subgroups \(\Leftrightarrow\) cyclic representations of categories.

  • Dual version?  Characteristic quotients (think Jacobson radical, Levi, etc.)
  • What about indecomposable repn? (Dunno, do you?)
  • What about other reps?  (Gotta PhD student without a problem?)
  • How are you gonna compute this?  (That we can talk about.)

Remarks

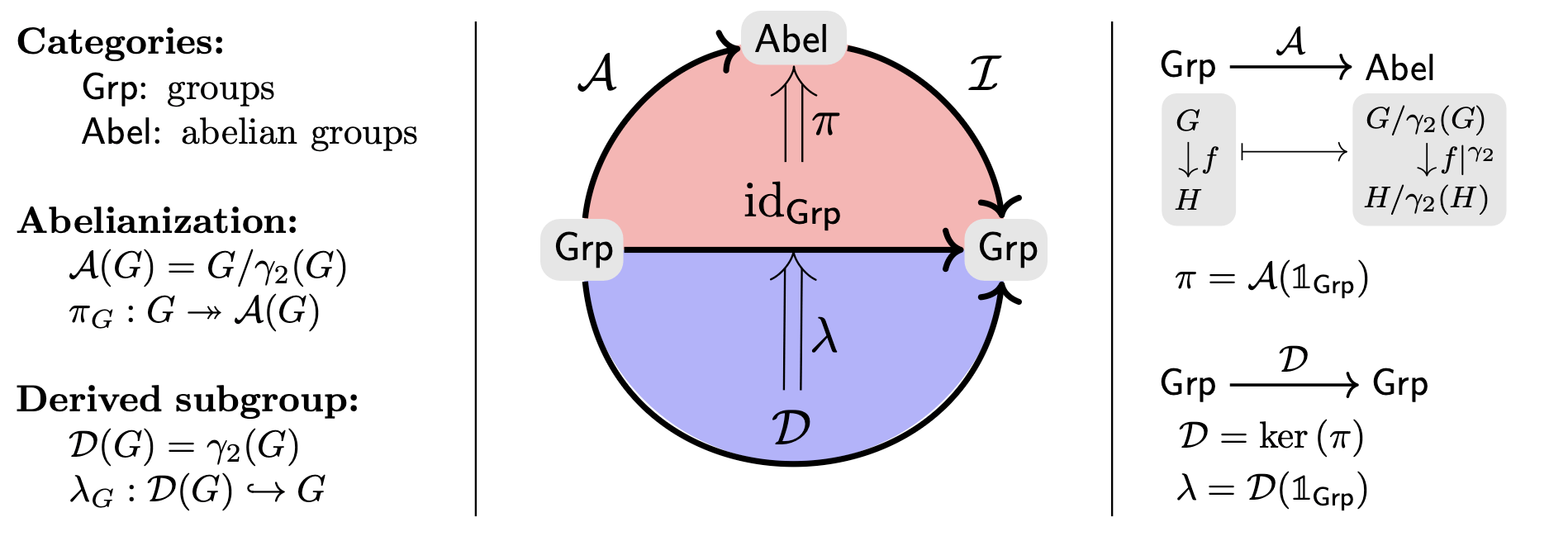
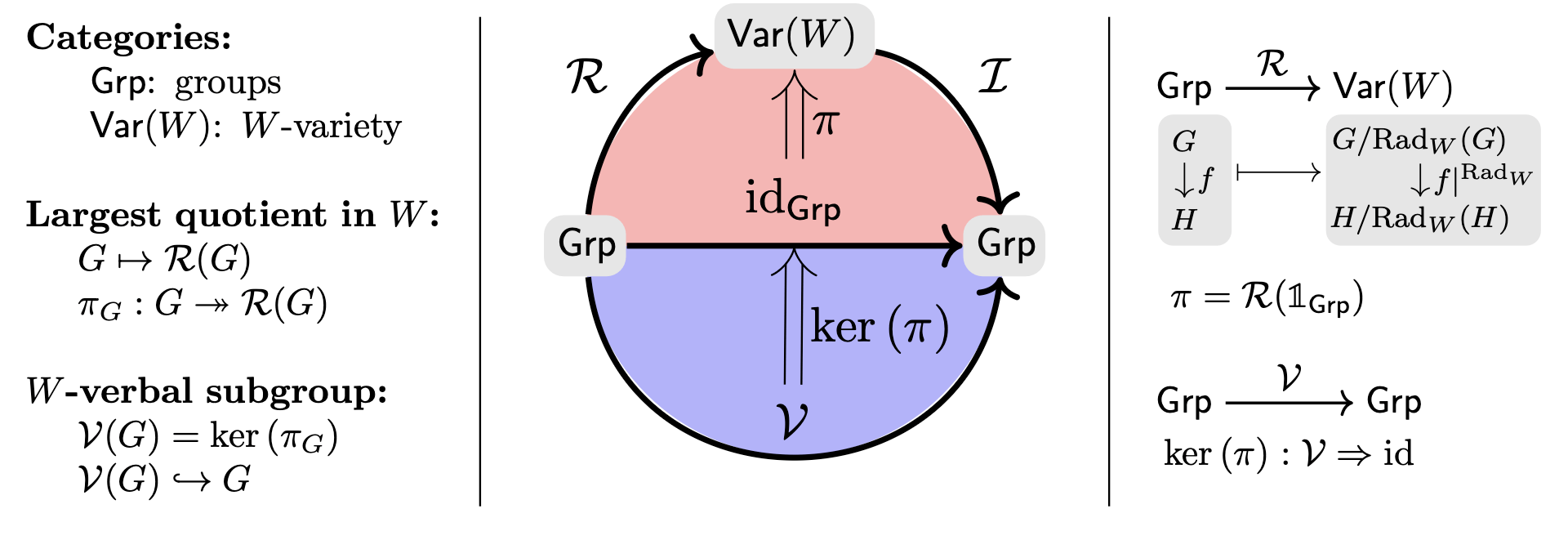
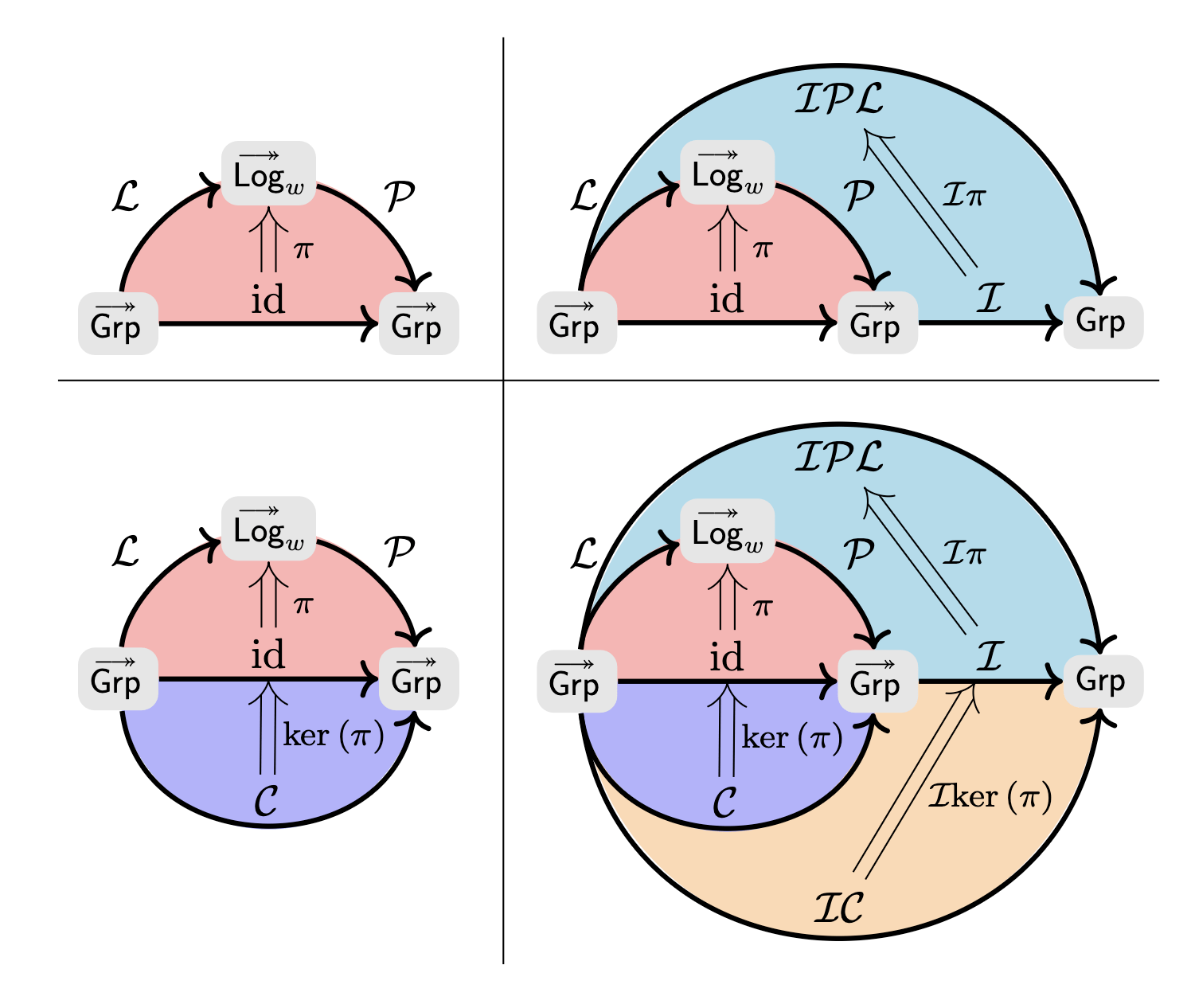
Pictures are nice but once you understand the algebra here is what a real characteristic subgroup construction now looks like:

 

\[\Delta\otimes_B\Gamma\otimes_A \Psi = G\cdot \mu \cdot S\]

 

It's just algebra.

Characteristic

Characteristic

Substructure or partitions that do not change under automorphisms.

1.

Category Actions

Categories acting is more intuitive than groups acting.

2.

Characteristic = biaction homomorphisms.

A complete description of characteristic without involving isomorphisms.

3.

  • Algebra is the computational arm of math.
  • Here the data are programs.
  • Need a Type Theory ("Proofs as Programs"). 
  • Prototyping in Agda
  • Certificate of characteristic comes from the type theory.

 

Code

Code we had before

is not far off

> H, iota := LMGFittingSubgoup(G);
\begin{array}{l|lcl} & C & \overset{\iota}{\Rightarrow} & 1\\ \hline G & C(G)~~ & \overset{\iota_G}{\hookrightarrow} & 1(G)~~\\ \downarrow \varphi& \downarrow C(\varphi) & & \downarrow \varphi\\ K & C(K)~~ & \overset{\iota_{K}}{\hookrightarrow} & 1(K)~~\\ \end{array}

We need to complete this to a functor and include types, but the spirit is there.

Experience on Programming proofs


-- A group homomorphism is a function that preserves the group structure
record GroupHomomorphism {A B : Set} (G : Group A) (H : Group B) : Set where
  field
    map : A → B
    -- Preserve multiplication: f(x · y) = f(x) ·' f(y)
    preserveMult : (x y : A) → 
      let _·ᴳ_ = AlgeStruct.ops (Group.algebra G) (# 0)
          _·ᴴ_ = AlgeStruct.ops (Group.algebra H) (# 0)
      in map (_·ᴳ_ (x ∷ y ∷ [])) ≡ (_·ᴴ_ (map x ∷ map y ∷ []))
    -- Preserve identity: f(e) = e'
    preserveId : 
      let eᴳ = AlgeStruct.ops (Group.algebra G) (# 1) []
          eᴴ = AlgeStruct.ops (Group.algebra H) (# 1) []
      in map eᴳ ≡ eᴴ
    -- Preserve inverse: f(x⁻¹) = f(x)⁻¹
    preserveInv : (x : A) → 
      let invᴳ = AlgeStruct.ops (Group.algebra G) (# 2)
          invᴴ = AlgeStruct.ops (Group.algebra H) (# 2)
      in map (invᴳ (x ∷ [])) ≡ (invᴴ (map x ∷ []))

Needs some heavy-hitting Type Theory


-- Define the equivalence relation as path constructors within the HIT
-- Example: Integers modulo 2
data ℤmod2 : Type where
  # : ℕ → ℤmod2
  -- Path constructor to identify pos n and neg n for n > 0
  mod2 : (n : ℕ) → # (suc (suc n)) ≡ # n

Our prototype works with cubical Agda with a Higher Inductive Type with Univalence Axiom

 

An Observational Type Theory is another potential strategy.

  • Lisp/Haskell dialect very mathematical, nothing like Java/Python/GAP/Magma/Sage
  • MathLib Lean Project community of support, goals are documenting proofs not so much computation.
  • Agda, Rocq/Coq.  Test out what types work for you.
  • Best advice: you likely have software already designed around your needs.  See these others as places to test out new constructs and import the ones that will help your system thrive.

Remarks

Teaching? Try Lurch

Five Guys THANK YOU

  • Selfish characteristics make mistakes.
  • Expand the language of categories to simplify them into models of algebra.
  • The representation theory of categories controls all characterisitics.
  • Proofs as programs is a reality, and it might be more useful to learn than anything I said today.

Summary

Characterizing Characteristic (50 mins)

By James Wilson

Characterizing Characteristic (50 mins)

Characteristic structure is information that does not change under isomorphisms. If you have all the isomorphisms you can verify this property. But we often need characteristic structure to find the isomorphisms: Chick-and-egg problem. This presentation reports on a new result that solve this problem.

  • 48

More from James Wilson