Primitive Functions
Combinators: functions without variables
2021 James B. Wilson, Colorado State University

\[\mathbb{SIKII}\rhd \mathbb{SKI}\]
Functions are made
of simpler functions,
made of simpler functions...
then even simpler functions...
...turtles all the way down or are some functions atoms?
mov dx, 0
mov ax, 7048 ; load n = 7048
mov bx, 541 ; load m = 541
div bx ; now bx=13 (q) AND dx=15 (r)Machine Language/ Assembly as atomic functions
But x86 is an industry choice.
Math like this came before...and probably will out last x86.
Combinators
Atomic functions need
- names, e.g. \(\mathbb{S}\), \(\mathbb{K}\), \(\mathbb{I}\), but also , \(\mathbb{C}\), \(\mathbb{D}\), \(\mathbb{Y}\)...
- yes ``\(\mathbb{Y}\)-combinator'' is a math not business. Thanks Turing (sorry Graham).
- Combined in ordered lists, e.g. \(\mathbb{SKI}\)
Combinators do not need input variables.
Hence have no domains and codomains.
TLDR: Variables are symbols outside the alphabet; so, the following are technically rubish
"\(x:=5\)", "if \(y=2\) then ..."
Variables are never assigned, never equal any thing. They only locate substitution.

Atomic Function \(\mathbb{I}\):
\(\mathbb{I}\)dentity Functions
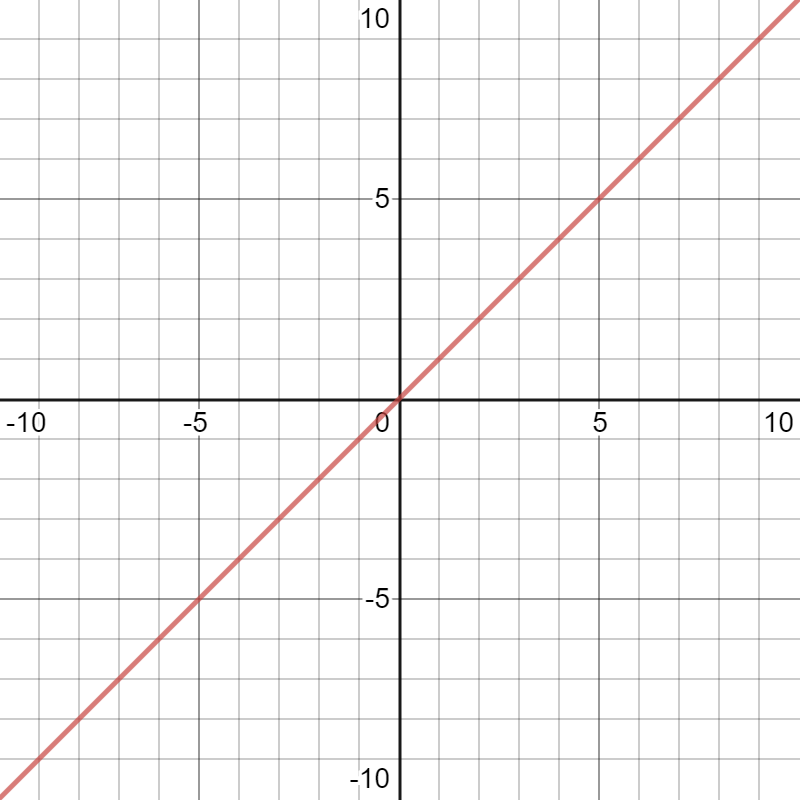
\(y=x\)
\(x\mapsto x\)
\(I(x)=x\)
What is missing?
- No domain
- No codomain
- Only one identity function
The
x
Atomic Function I:
Identity Functions
Characterize \(\mathbb{I}\) by
\[\mathbb{I}V\rhd V\]
That is our first (weak) reduction rule.
The
x
TMI
-
Why \(\rhd\) instead of \(=\) or `:=`?
-
It is neither equal nor assigned. It is verb is reduce, so use reducing symbol.
Atomic Function \(\mathbb{K}\):
\(\mathbb{K}\)onstant Functions
\(y=3\)
\(x\mapsto \alpha\)
\(\mathbb{K}_c(x)=c\)
Still no domain/codomain.
- Still one function
- Just Two "inputs"
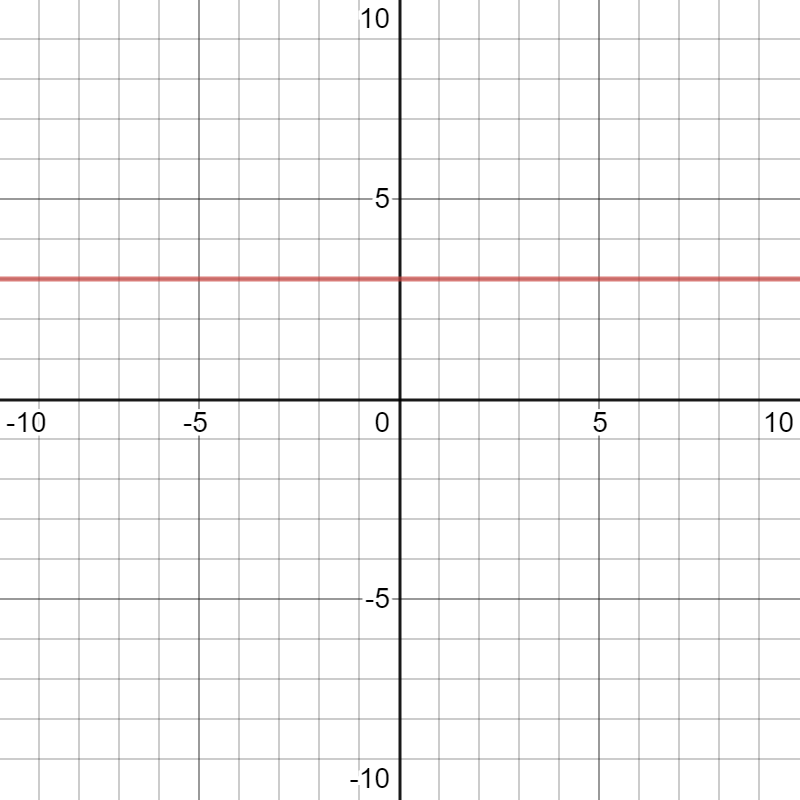
The
x
Characterize \(\mathbb{K}\) by
\[\mathbb{K}UV\rhd U\]
That is our second (weak) reduction rule.
Again... not equal, not assigned, reduced.
Atomic Function \(\mathbb{K}\):
\(\mathbb{K}\)onstant Functions
The
x
Can't \(\mathbb{SKI}\) without an \(\mathbb{S}\)
Identity and constants are interesting, but we need real programs to choose a path.

Atomic Function \(\mathbb{S}\):
\(\mathbb{S}\)hoenfinkel Composition
Some logic needs to branch.
- First, offer a path off the main, \(g(x)\).
- Second, decide what to do with both paths, \(f(x,g(x))\).
- E.g. pick a side.
def branch(P)(x) = {
if P then
x
else
g(x)
}
f after branch\(S_{f,g}(x)=f(x,g(x))\)
\(\mathbb{S}_{f,g}(x)=f(x,g(x))\)
\[x\mapsto (x,g(x))\mapsto f(x,g(x))\]
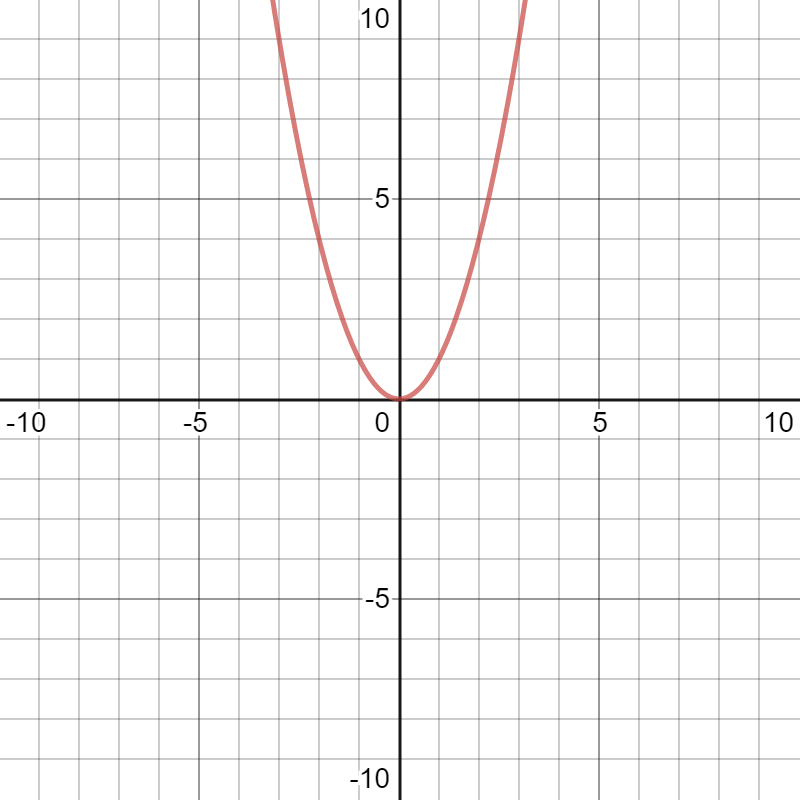

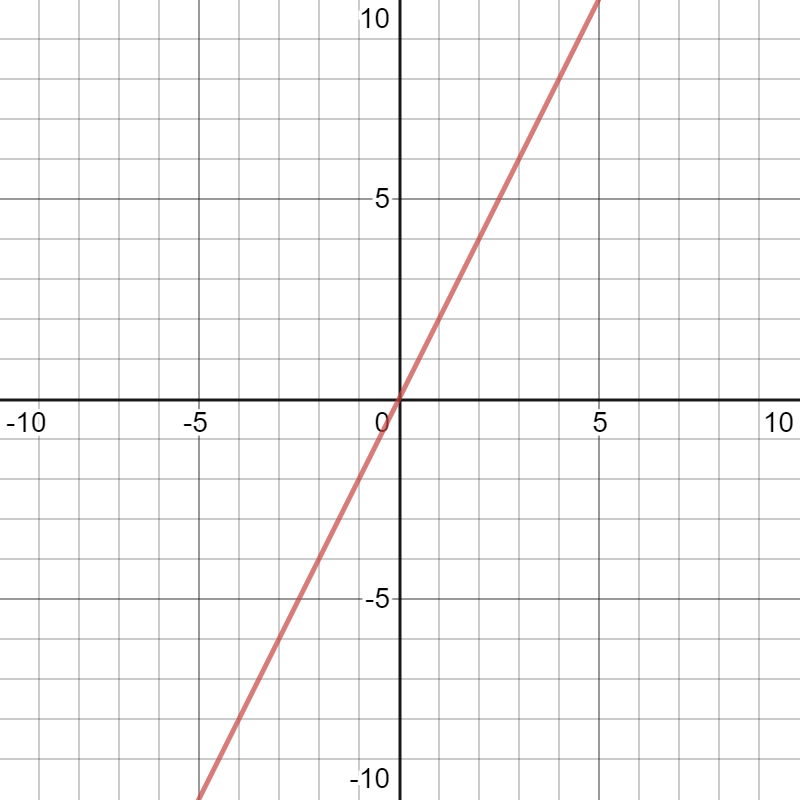
\(d/dx\)
\(x\mapsto x^2\)
Atomic Function \(\mathbb{S}\):
\(\mathbb{S}\)hoenfinkel Composition
You don't have to branch, you might both paths!
Characterize \(\mathbb{S}\) by
\[\mathbb{S}UVW\rhd UW(VW)\]
That is our third (weak) reduction rule.
Atomic Function \(\mathbb{S}\):
\(\mathbb{S}\)hoenfinkel Composition
Pure Combinators
Informally
- \(\mathbb{I}(x)=x\)
- \(\mathbb{K}_c(x)=c\)
- \(\mathbb{S}_{f,g}(x)=f(x,g(x))\)
Pure
Combinators
Logically
- \(\mathbb{I}U\rhd U\)
- \(\mathbb{K}UV\rhd U\)
- \(\mathbb{S}UVW\rhd UW(VW)\)
But wait there is more...
- SKI-combinators are the pure combinators. Enough to describe all computable functions.
- Other combinators offer short cuts, e.g. to recursion (Barney R or Turing Y combinators).
- Applied combinators, such as most instructions in x86 are not necessary for math but surely make functions shorter, faster, and easier to understand.
Further Reading
- Hindley-Seldin Lambda-Calculus and Combinators, Cambridge U. Press, Chapter 1.
Primitive functions: Combinators
By James Wilson
Primitive functions: Combinators
Many functions we use are built from simpler functions and that explains all the qualities of functions: predictable outputs for example. So where does this process get started? What are primitive functions?
- 705



