Tensors by volume
2025 James B. Wilson


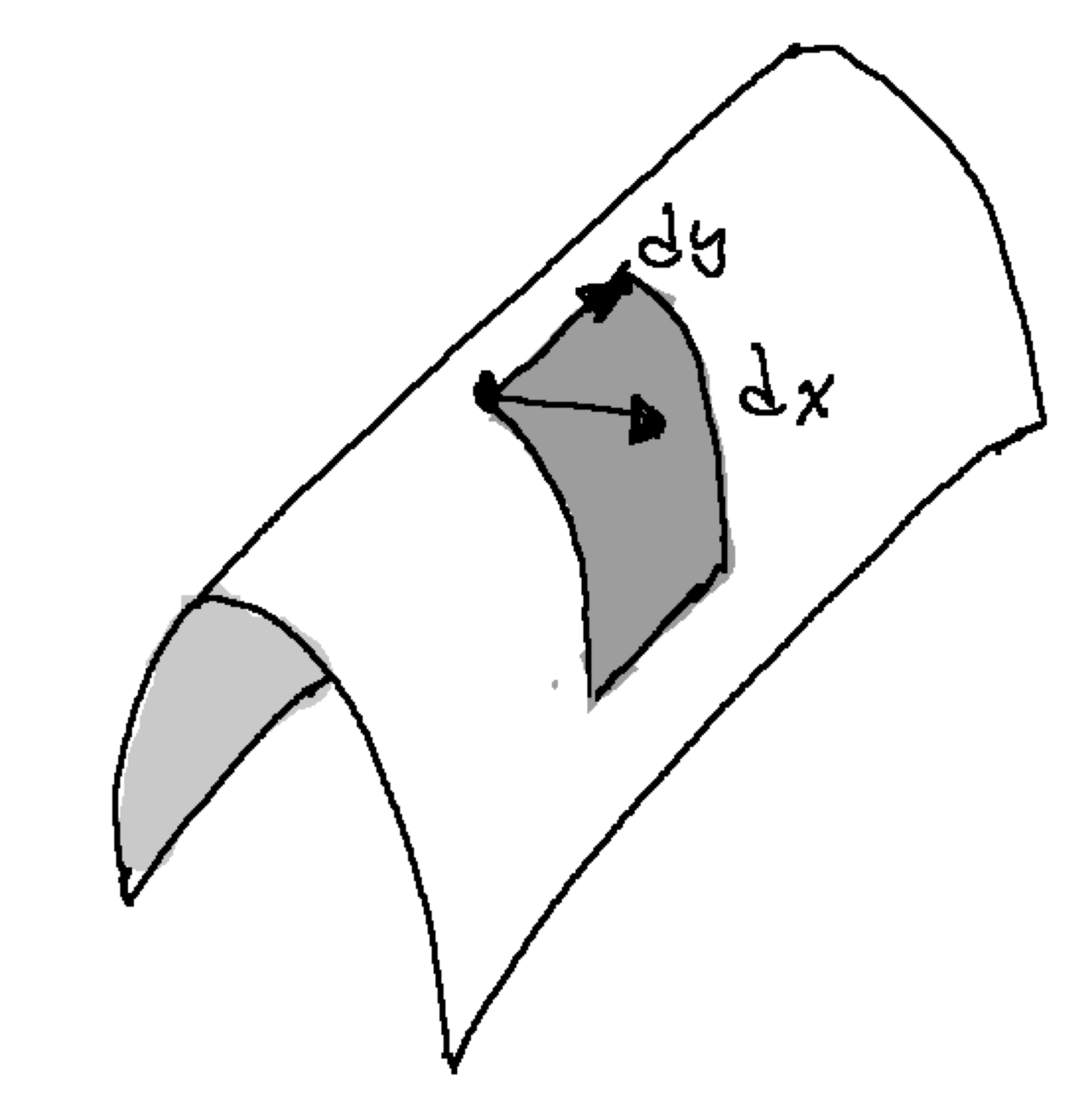
Volume basics
\[Vol(\ell, w,h)= \ell\times w\times h\]


Volume reality
\[Vol(t\mid \ell, w,h)= t\times \ell\times w\times h\] where \(t\) converts miles/meters/gallons/etc.
tensor conversion
Miles
Yards
Feet
Gallons
Area...easy
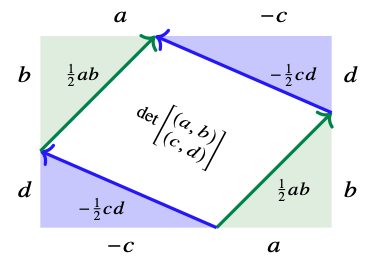
Area...not so easy

\[det\left(\begin{array}{c} (a,b)\\ (c,d)\end{array}\right) = ad-bc\]
\[= \begin{bmatrix} a & b\end{bmatrix}\begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix}\begin{bmatrix} c\\ d \end{bmatrix}\]
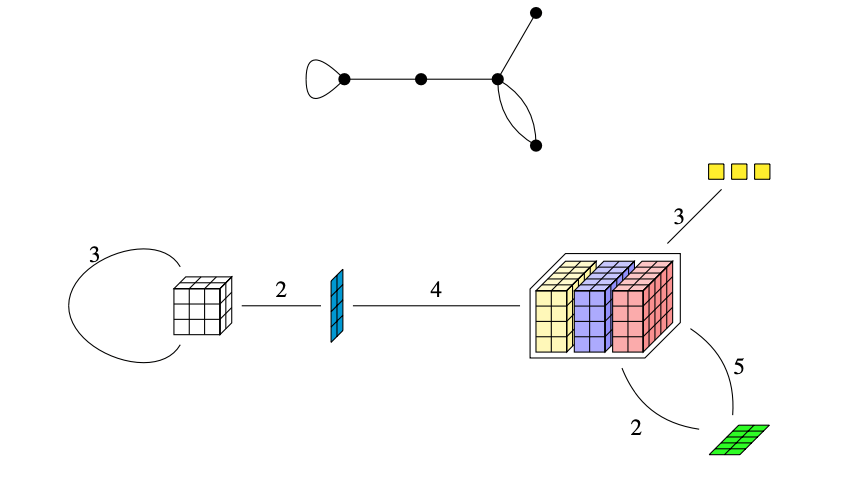
tensor
Area...getting worse

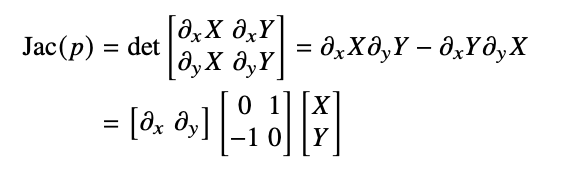
Facts?

Facts?
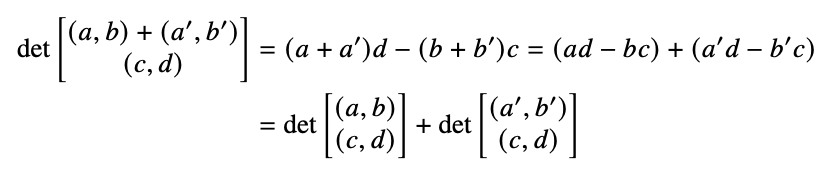
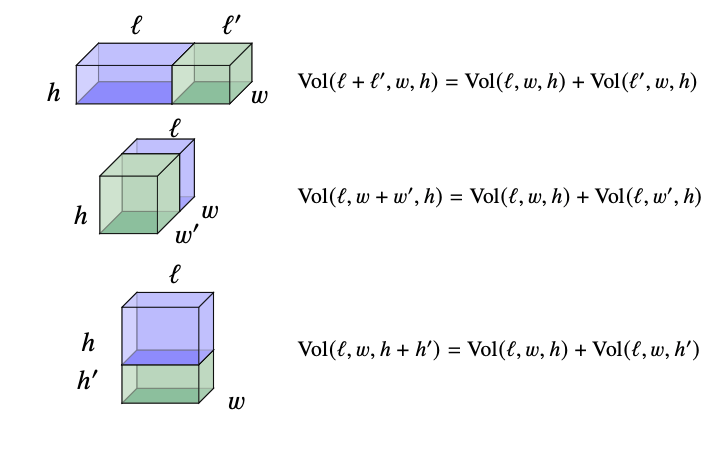
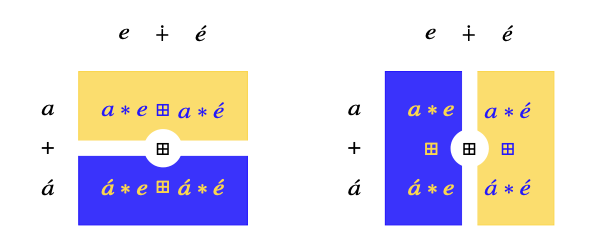
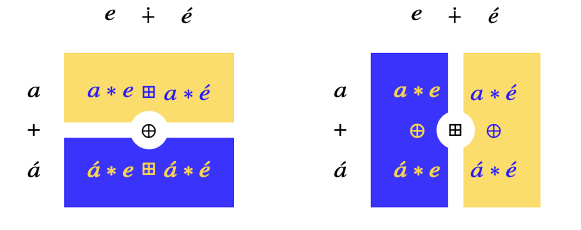
Distributive dicta
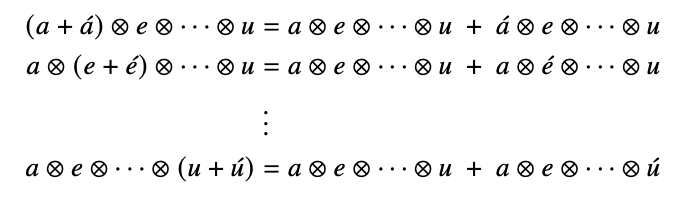
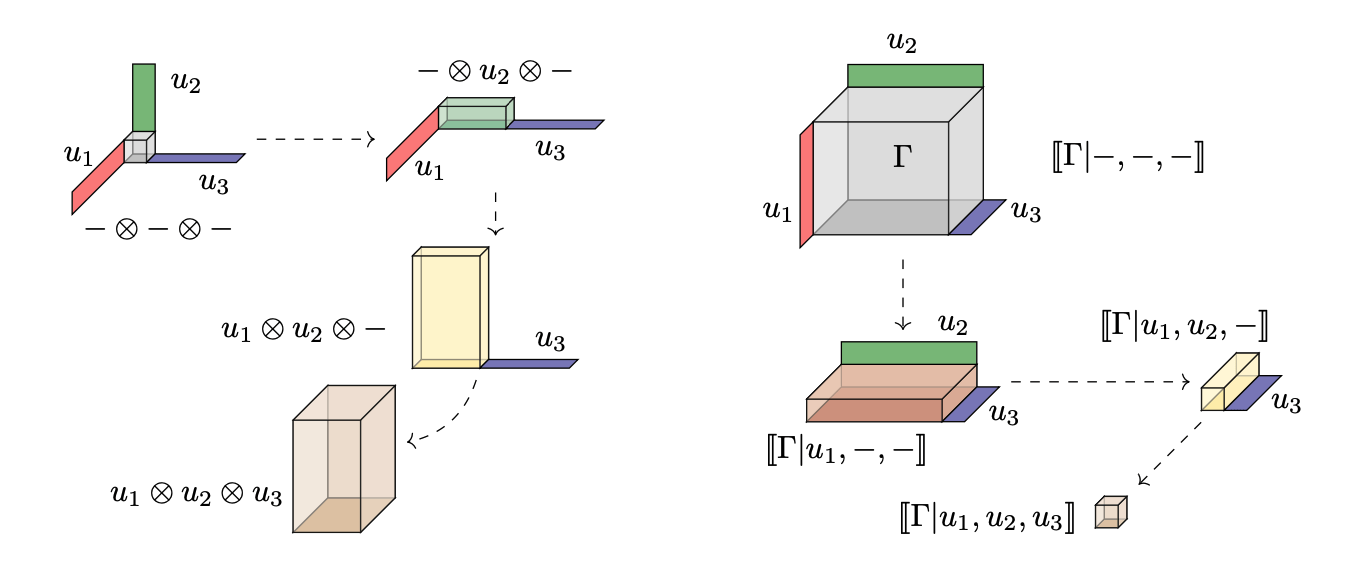
Products can grow bigger (inflation)
or get smaller (contraction)
Moral: tensors are the multiplication tables of distributive products.
Tensor contraction/inflation is just jargon for what happens when we take the products
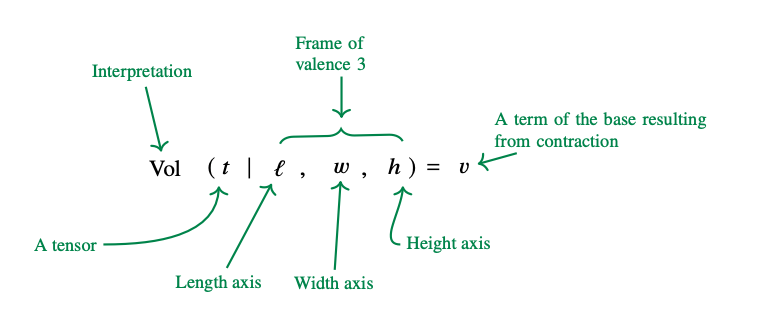
jargon
New uses? Make up new measurements

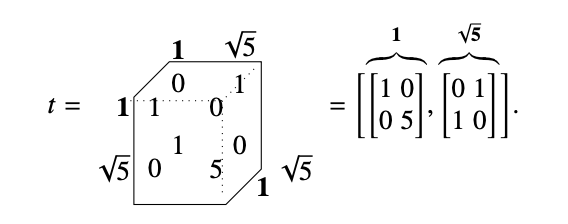

New uses? interactions probabilities and quantum information
New uses? Sales Volume?
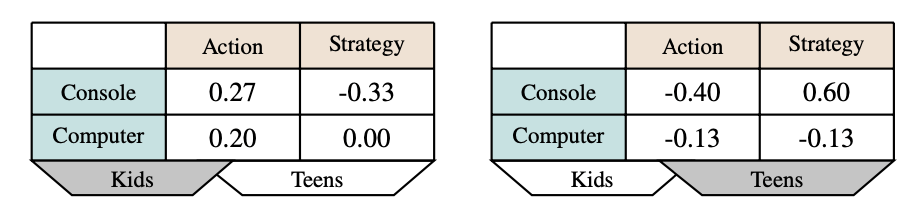
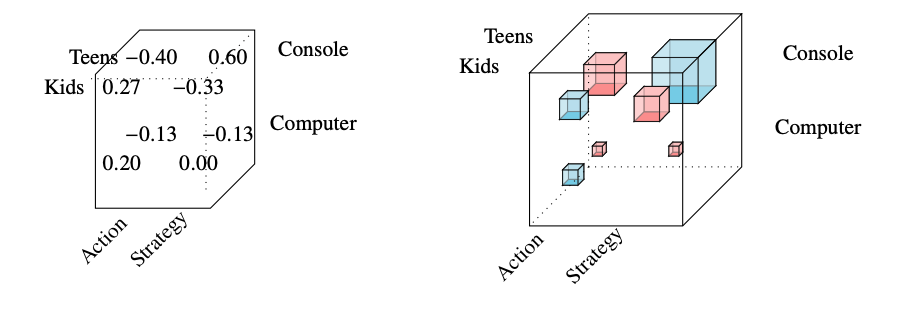
Consequences
Consequences?

Consequences?


Real Consequences?

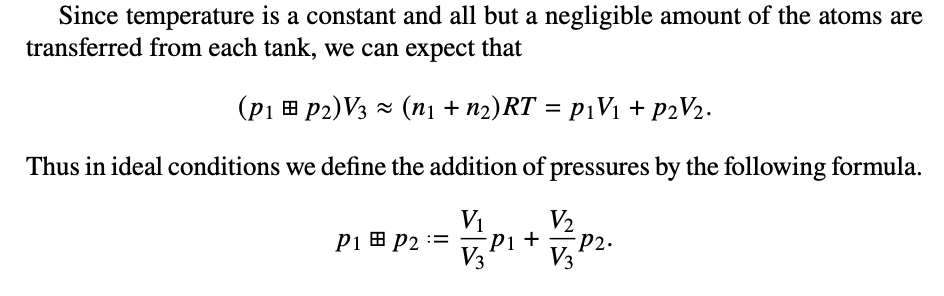
Real Consequences?
Entropic Edict/ Fubini Formula
\[\int_I \int_J \langle a_i, e_j,\ldots \rangle d\mu d\nu = \left\langle \int_I a_i d\mu, \int_J e_j d\nu,\ldots \right\rangle\]
\[=\int_J\int_I \langle a_i, e_j, \ldots\rangle d\nu d\mu\]
If it is a tensor then you have algebra that distributes over entropic sums and integrals.
Tensors by volume
By James Wilson
Tensors by volume
A visual tour of how volume leads to tensors.
- 236



