Function Factories
(The Exponential)
2025 James B. Wilson

Not all functions are created as functions.
-
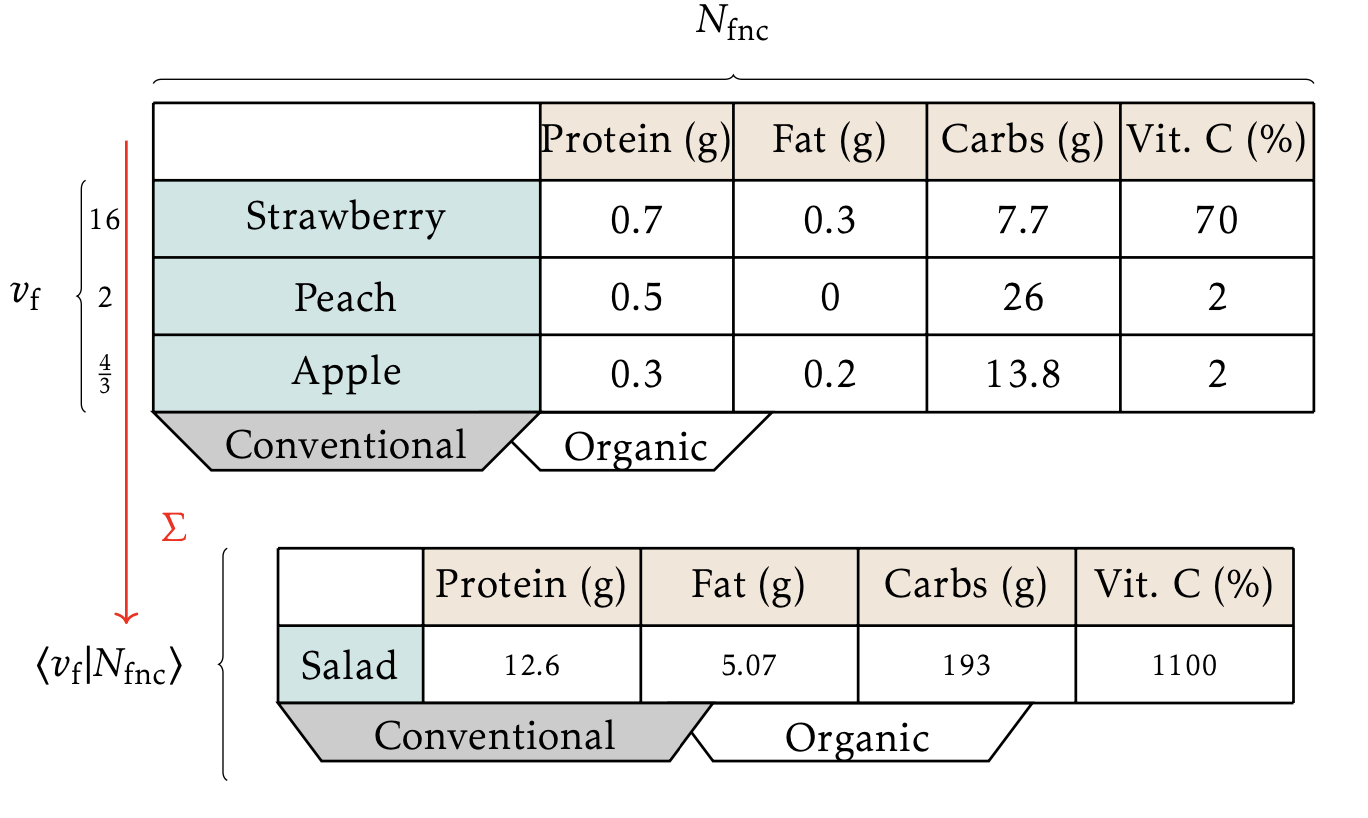
The USDA has made nutrition charts of fruit.
-
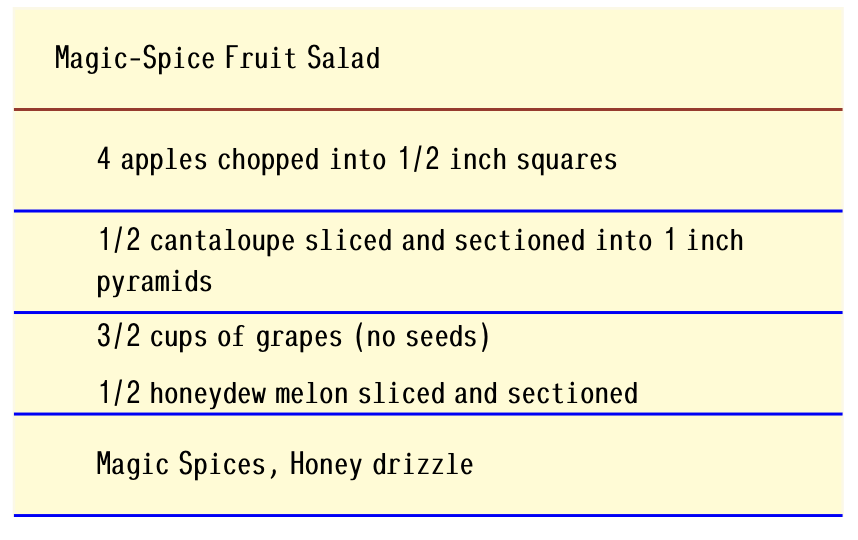
You have a fruit salad recipe, and it's not on the USDA chart!

GOAL:
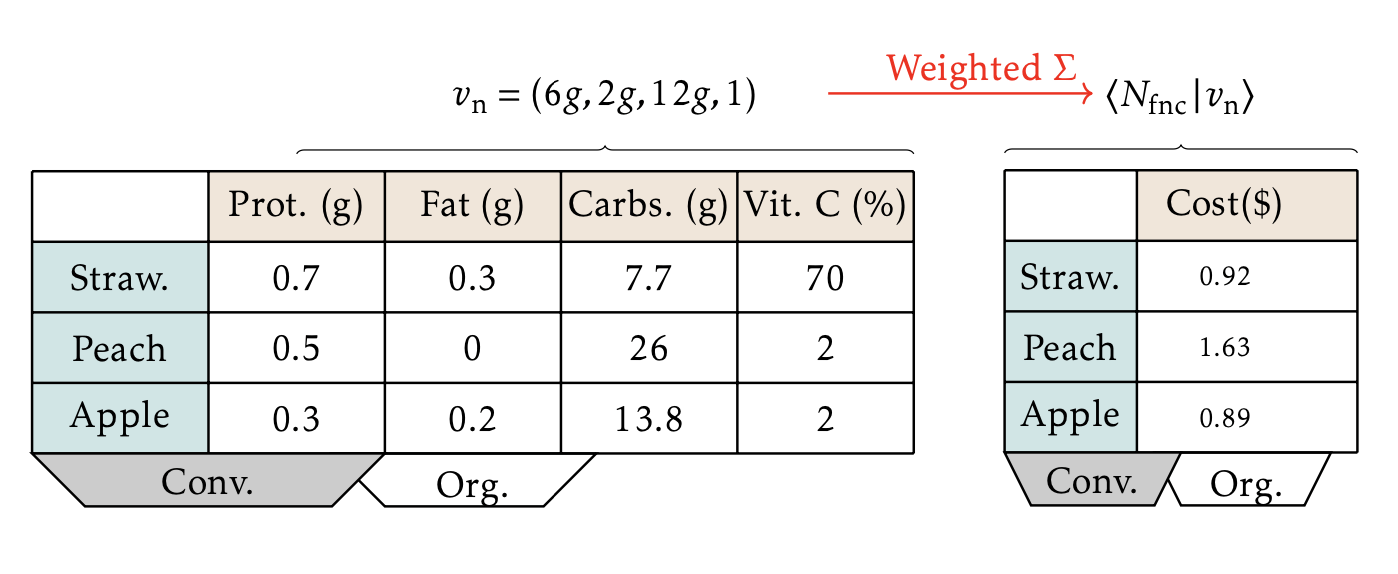
Use chart to
Turn Recipes into Nutrients




An algorithm...

A FUNCTION
FACTORY:
New chart C =>
New Function:
eval (C): Recipe -> Nutrient





A FUNCTION
FACTORY Type?:
New data F:?? =>
New Function:
eval(F):A -> B
\(F:??\)
\(a:A\)
\(eval(F)(a):B\)
\[eval:??\times A\longrightarrow B\]
Previous Lessons
Work for a universal type
\(A\)
\(B\)
\(B^A\times A\longrightarrow B\)
Formation
\(B^A\times A\longrightarrow B\)
\(C\times A\longrightarrow B\)
\(B^A\times A\longrightarrow B\)
\(C\times A\longrightarrow B\)
Introduction
\[\frac{f:C\times A\to B\quad c:C}{c^f : B^A}\]
Elimination
\[\frac{F:B^A\quad a:A}{F\, @\,a :B}\]
Computation
\[\begin{array}{rl} f&:C\times A\to B\\ c&:C\\ a&:A\\ \hline c^f\, @\, a&:=f(c,a)\end{array}\]
This is not a cone!
Still can be universal if competes with alternatives
\(@\)
\(@\)
\(@\)
\(f\)
\(f\)
\(c^f\)
A FUNCTION FACTORY:
\[\frac{\Gamma\vdash A,B:Type}{\Gamma\vdash B^A:Type}\qquad(Form_{exp})\]
\[\frac{\Gamma\vdash f:C\times A\to B,\quad c:C}{\Gamma\vdash c^f:B^A}\qquad(Intro_{exp})\]
\[\frac{\Gamma\vdash F:B^A,\qquad a:A}{\Gamma\vdash F\, @\, a:B}\qquad(Elim_{exp})\]
\[\frac{\Gamma\vdash f:C\times A\to B,\qquad a:A}{\Gamma\vdash (c^f\, @\,a) := f(c,a)}\qquad(Comp_{exp})\]
interface AsFunction<A,B,C> {
B apply(C c, A a);
}
/* Form: B^A */
class Exp<B,A> {
AsFunction myf; C myC;
/* Intro: c^f */
Exp(AsFunction f, C c) {
myf=f; myC=c; // Comp 1: You engineering here
}
/* Elim: F @ a */
B apply(A a){
return myf(myC,a); // Comp 2: Or here
}
}
Java Demonstration
\[\frac{A,B:Type}{ B^A:Type}\quad(Form_{exp})\]
\[\frac{f:C\times A\to B,\quad c:C}{c^f:B^A}\quad(Intro_{exp})\]
\[\frac{F:B^A,\qquad a:A}{F\, @\, a:B}\quad(Elim_{exp})\]
\[\frac{f:C\times A\to B,\qquad a:A}{(c^f\, @\,a) := f(c,a)}\quad(Comp_{exp})\]
AsFunction<int,String,Object> f = ...
String c = ...
Exp<int,String> fAsNewFunc = new Exp(f,c);
fAsNewFunc.apply(5);Elim Intro
Don't need to replace ALL functions.
/*
* Convert (ImageTypeSpecifier, ImageReader) -> ImageWriter
* To ( MyImageProcess, ImageReader) -> ImageWriter
*/
class MyImageProcess<B extends ImageWriter, A extends ImageReader> {
/* Intro: c^f */
MyImageProcess(ImageTranscoder currentFormat, ImageTypeSpecifier type) {
// Adjust paramters to convert types by you methods
}
/* Elim: F @ a */
B apply(ImageReader img){
// Convert the image
}
}
E.g. Image processing has many algorithms, want to convert functions between image formats.
Limit A < ImageReader, B < ImageWriter and \(f:C\times A\to B\) to ImageTranscoder x ImageReader -> ImageWriter
Other Syntax
class Exp[B,A]( f:(C,A)->B, c:C) {
def '@'(a:A):B = f(c,a)
}
> c:C = ...
> f:(C,A)->B = ...
> e:Exp[B,A] = Exp(f,c)
> a:A = ...
> e @ a
data Exp a b
infix ^ : (c:C) -> (f:(C,A)->B) -> Exp a b
infix @ : (e:Exp a b) -> (a:a) -> B
@ (c f) a = f c a
c:C = ...
f:(C,A)-> B = ...
a:A = ...
c ^ f @ a
...but replace with a useful conversion.
Exponentials
- Capture functions \(A\to B\)
- Let you store/apply those functions however you need.
- Are universal programs so they plan ahead for changes.
\(A\)
\(B\)
\(B^A\times A\longrightarrow B\)
\(@\)
\(B^A\times A\longrightarrow B\)
\(C\times A\longrightarrow B\)
\(@\)
\(f\)
\(B^A\times A\longrightarrow B\)
\(C\times A\longrightarrow B\)
\(@\)
\(f\)
\(c^f\)
Exponentials
By James Wilson
Exponentials
- 305


