Phase of matter

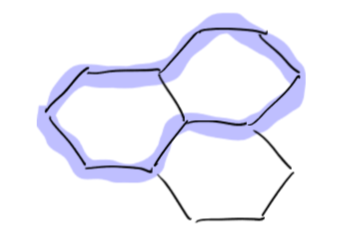
Graphite

Diamond

Images Wikipedia Public Domain

Different (idealized) symmetry groups

<=>

Different phases of matter under Landau taxonomy

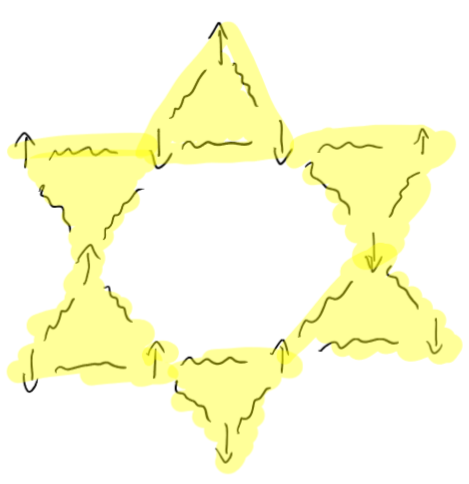
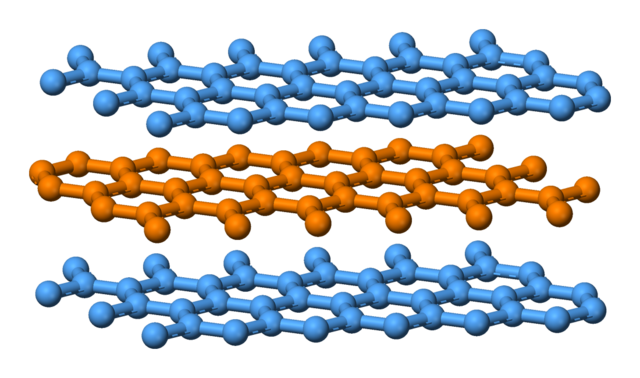
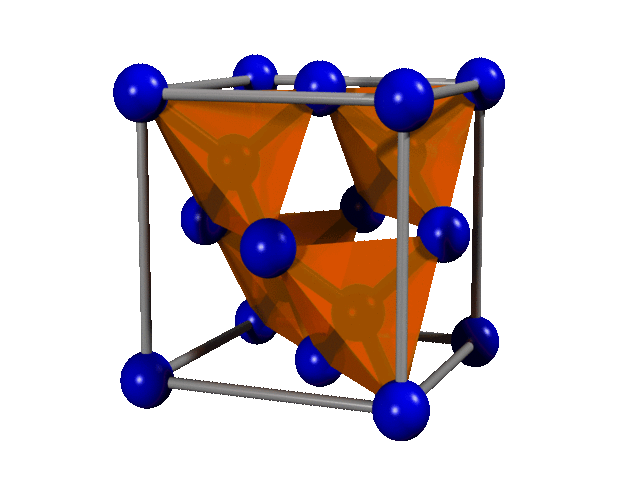
Herbertsmithite

\(Zn(Cu)_3(OH)_6 Cl_2\)

Images CC-BY Rob Lavinsky

structure of a "quantum spin liquid"

• quantum spin -- up/down config of particles
• liquid -- continuous translation symmetry == chaotic
• clearly not a liquid so symmetry group is misleading, suggests phases of matter beyond obvious

CC BY Tomruen

Kagome Lattice structure at the level of molecule interactions

Planned applications

• Superconducting and magnets
• Quantum computers
• Warp drive -- just kidding, but place holder for stuff we haven't even imagined yet.

Summary

• Phases of matter separated by symmetries (groups + representation)
• "Symmetry breaking" where new group/rep appear.
• Once on the level of atoms & molecules.
• Some material properties only explained by symmetries at quantum level (subatomic) "(Topological) Quantum Phases of Matter"

Topological? I.e based on "Topological Quantum Field Theories (TQFT)"

Quantum Mechanics as Mathematics

(For the physics go read Isaac Asimov)

"particle" states are (unit) vectors \(|v\rangle\) in Hilbert Space \(\mathcal{H}=\mathbb{C}^d\) e.g. electron spin is a basis of \(\mathbb{C}^2\)\[|v\rangle \in \{|\uparrow\rangle,|\downarrow\rangle\}\]

 

"waves" are density matrices \(|v\rangle\langle v|:\mathcal{H}\to \mathbb{C}\to \mathcal{H}\) \[|\uparrow\rangle\langle \uparrow|=\begin{bmatrix}1\\ 0 \end{bmatrix}\begin{bmatrix} 1 & 0\end{bmatrix}=\begin{bmatrix}1 & 0 \\ 0 & 0 \end{bmatrix}\]

\[|\downarrow\rangle\langle \downarrow|=\begin{bmatrix}0\\ 1 \end{bmatrix}\begin{bmatrix} 0 & 1\end{bmatrix}=\begin{bmatrix}0 & 0 \\ 0 & 1 \end{bmatrix}\]

(see the particle/wave duality?)

\(n\)-body systems \(\mathcal{H}_1\otimes\cdots\otimes \mathcal{H}_n\),

 

E.g. Electron orbital in an atom's shell \(\mathbb{C}^2\otimes \mathbb{C}^2\) \[\begin{aligned}|\psi\rangle & =\frac{\sqrt{2}}{2}(|\downarrow\uparrow\rangle-|\uparrow\downarrow\rangle)\\ & =\frac{1}{2}\begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix}\end{aligned}\]

entanglement = \(|\psi\rangle\) where \(|\psi\rangle\) has rank more than 1.

How stuff changes

(a mostly true version)

• Particles come within Planck length,
• Heisenberg uncertainty \(\Rightarrow\) at that scale particles can burst into existence, so long as gone by sun down (Planck time), so "virtual particles"

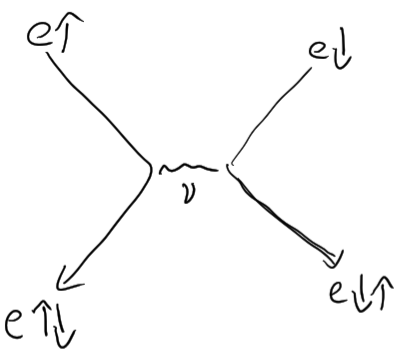
How stuff changes

(a mostly true version)

• entangled particles have exchanged some virtual particles, surplus/deficit now in common, but its "random" you cannot say who got what
• because virtual particle exchange is net zero, i.e reversible, model by unitary \(U|\psi\rangle\)

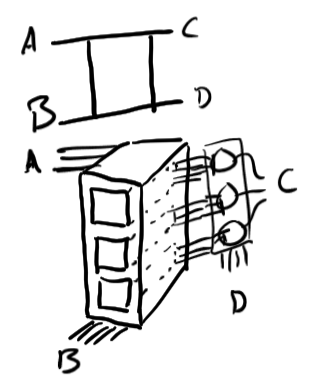
How we measure stuff

(a mostly true version)

Measurement is forcing/allowing entanglement with target particles \(|M\rangle\),

 

cause a cascade of entanglements

which then favors electric circuits (e.g. making all spin up so fero-magnetic state) in some brain cells and not others.

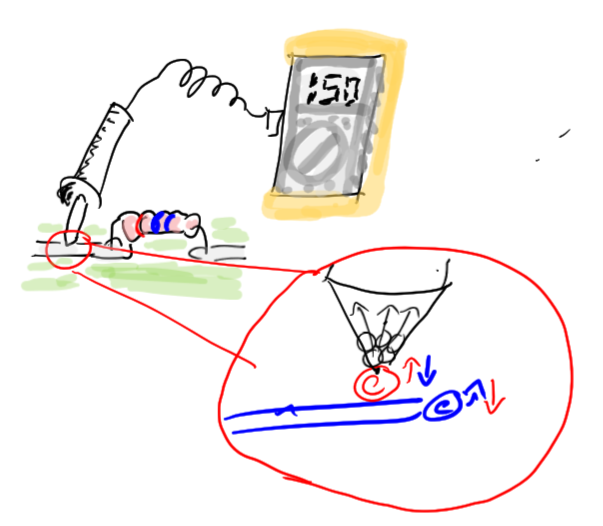
Random outcome caused by virtual particle exchange

Top. Quant. Phs. Mat. as Tensor Networks

(now you wish you had paid attention in talk 1)

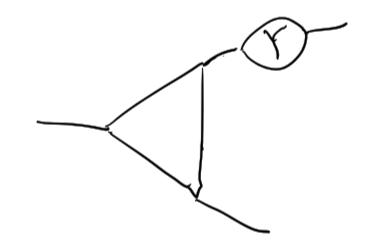
States are vectors in Hilbert space, (vertices)

entanglements are unitary (squiggles)

many body systems are in tensor product, ...so these interact as tensor networks

Short range (gapped) entanglements between spins

Frustrated configuration so "liquid" symmetry group

Herbertsmithite

States are vectors in Hilbert space, (vertices)

entanglements are unitary (squiggles)

many body systems tensor product,

Virtual (gapless) entanglements between spin singlets "orbitals"

Stable configuration so "solid" Symmetry Protected (local changes nudge back)

Quantum Insulator! (robust to quantum noise at low energy)

P.E.P.S.

Projected Entanglement Particle Sys.

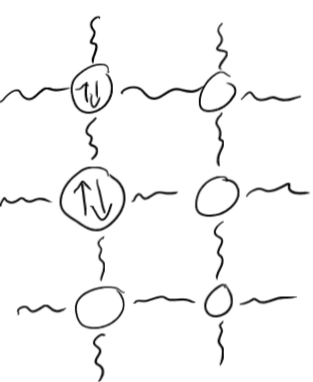
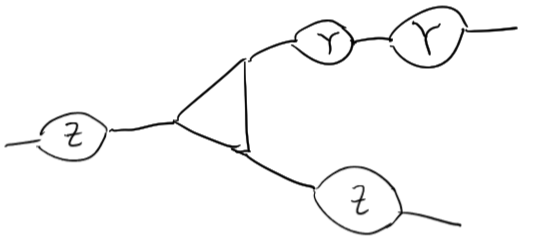
States are vectors in Hilbert space, (vertices)

entanglements are unitary (squiggles)

many body systems tensor product,

Long range entanglements, move things around each other.

Stable configuration so "solid" Symmetry Protected (local changes nudge back)

Topological Quantum Conductor! (hold entanglements robust to noise)

Kitaev Anions

Large scale physics of QM

(Tensor Isomorphism)

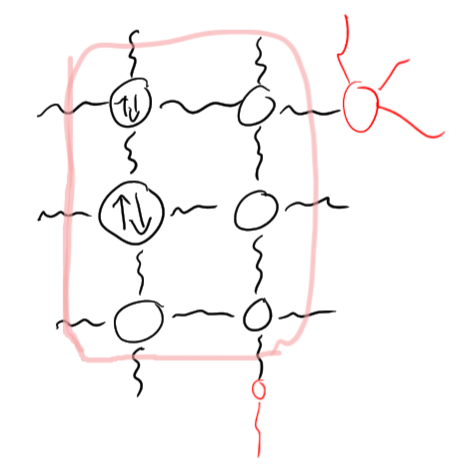
A quantum material such a PEPS somewhere has a boundary that interacts with environment.

 

 

 

 

 

 

 

The physics you see is on this boundary.

What is that physics?

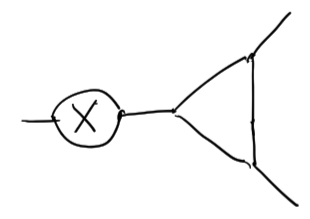
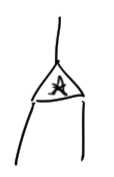
Theorem (First-Maglione-W.)

All transverse symmetry groups of tensors are defined by toric ideals with binary support.  I.e. \(X^{\alpha}-X^{\beta}\) \(\alpha_i+\beta_i\leq 1\).

\(\neq\)

So data must flow over the particle it cannot spread out over the particle.

Tensor Isomorphism

The name for symmetries that flow over a tensor

large scale physics of tensor network is the intersections of the tensor automorphism groups.

For homogeneous lattice linked tensor networks it is a symmetrized subgroup of the automorphism group

Detecting Tensor net Iso

Tensor Product approximation

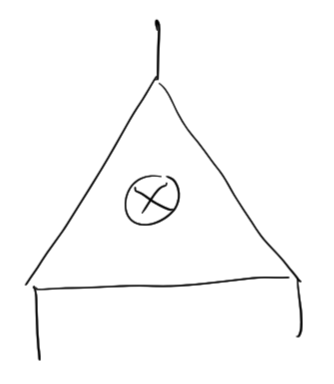
Detecting Tensor net Iso

(Brooksbank-W.) Adjoint-Tensor approximation

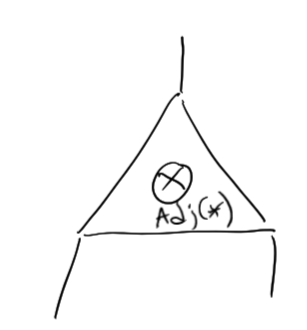
Solve linear equations (Sylvester equations!) to get good operators to reduce dimension.

Automorphisms approximate by \(Norm_{GL}(Adj(*))\)

Detecting Tensor net Iso

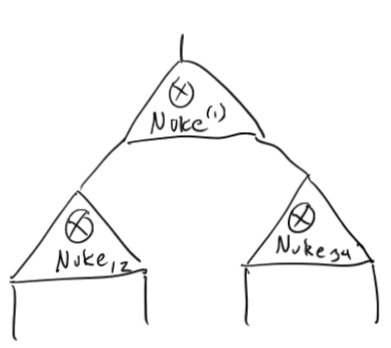
(Brooksbank-Kassabov-W.) Iterative Adjoint-Tensor-Network approximation (in progress)

An iterative approach which collapses lower cells in a simplicial complex to create local best approximations.