James B. Wilson


Reciprocal
\(\Delta y=\frac{\Delta y}{\Delta x}\Delta x\)
Integral
\(\int_{\Delta x} y\,dx\)
Derivative
\(\frac{dy}{dx}\)
Area
\(\Delta\)y \(\times\) \(\Delta\) x
Limits v's L
All but finitely many
v's within e decimal places of L.
Slope
\(\Delta\)y
\(\Delta\)x
Fundamental Theorem
of Calculus
\(\Delta y=\int_{\Delta x} \frac{dy}{dx} dx\)
Measure
\(\Delta u=b-a\)
\(a\)
\(b\)
{
\(\Delta u\)
\(\Delta y\times \Delta x\)
\(\Delta x\)
\(\Delta y\)
\(\Delta y/\Delta x\)
\(\Delta x\)
\(\Delta y\)
\(a\)
\(b\)
{
\(\Delta u\)
of the infinite approximations your could make, for any precision, all but finitely many are accurate
{
\(L\)
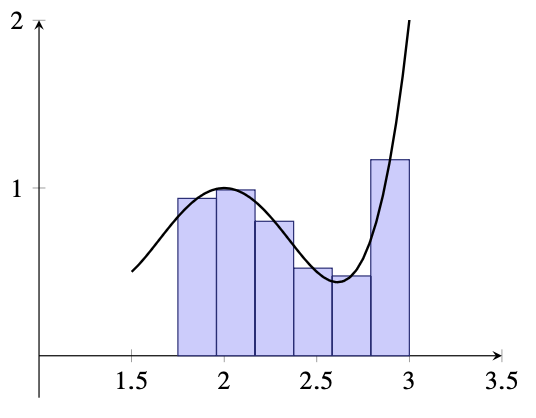
\[\int_{\Delta x} ydx=\lim \sum_i \Delta y_i \Delta x_i\]
\[\frac{dy}{dx} =\lim \frac{\Delta y_i}{\Delta x_i}\]
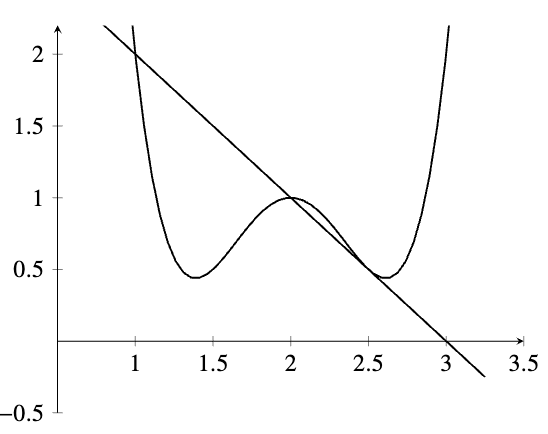
\[\Delta x = 5-3\qquad \int_{\Delta x} x^3 dx=?\]
\[\int_3^5 \frac{d}{dx}\left(\frac{x^4}{4}\right) dx=?\]
\[\int_{\Delta x} \frac{d}{dx}\left(\frac{x^4}{4}\right) dx=\Delta y=\frac{5^4}{4}-\frac{3^4}{4}\]
James B. Wilson


Integral
\(\int_{\Delta x} y\,dx\)
Derivative
\(\frac{dy}{dx}\)
Area
\(\Delta\)y \(\times\) \(\Delta\) x
Limits v's L
All but finitely many
v's within e decimal places of L.
Slope
\(\Delta\)y
\(\Delta\)x
Fundamental Theorem
of Calculus
\(y=\frac{d}{dx}\int_c^x ydx\)
Measure
\(\Delta u=b-a\)
Reciprocal
\(\Delta y=\frac{\Delta y\Delta x}{\Delta x}\)
\[\int_{\Delta x} \frac{1}{x} dx=?\]
\[\frac{d}{dx}(\ln x)=\frac{d}{dx}\int_{\Delta x} \frac{1}{x}dx=\frac{1}{x}\]
\[\ln x+C:=\int_c^x\frac{1}{x} dx\]
The Calculus
By James Wilson
The Calculus
- 255


