Types, Programs, & Categories

2023 James B. Wilson

Colorado State University

\begin{aligned} A & \overset{\pi_A}{\longleftarrow} & A\times B & \overset{\pi_B}{\longrightarrow} B\\ & f\nwarrow & \uparrow~~~~ & \nearrow g & \\ & & ~~T~~~~ & & \end{aligned}

class Pair<A,B> {
  A myA;
  B myB;
  Pair(A a, B b) { myA = a; myB = b;}
  
  A piA() { return myA; }
  B piB() { return myB; }
}

\begin{aligned} A,B:\mathcal{U} & \vdash A\times B:\mathcal{U} \\ a:A, b:B & \vdash (a,b):A\times B\\ x:A\times B & \vdash \pi_A(x):A \\ x:A\times B & \vdash \pi_B(x):B\\ a:A, b:B & \vdash refl: a=_A \pi_A(a,b)\\ a:A, b:B & \vdash refl: b=_B \pi_B(a,b)\\ \end{aligned}

Math

Programming

Logic

\begin{aligned} A & \overset{\pi_A}{\longleftarrow} & A\times B & \overset{\pi_B}{\longrightarrow} B\\ & f\nwarrow & \uparrow~~~~ & \nearrow g & \\ & & ~~T~~~~ & & \end{aligned}

class Pair<A,B> {
  A myA;
  B myB;
  Pair(A a, B b) { myA = a; myB = b;}
  
  A piA() { return myA; }
  B piB() { return myB; }
}

Knowing one of these?

Heard of a connection to the others?

Math

Logic

Programming

Three Steps to a Program

Reason about flow
Annotate the data
Match to Programming Idioms

\begin{aligned} \begin{array}{rl} \Gamma & \vdash A \\ \Gamma &\vdash B \\ \hline \Gamma & \vdash A\wedge B \end{array} \end{aligned}

Starting Point: reasoning

Conjunction:

context \(\Gamma\) (also ctx) says events A and B hold;
Make a single combined event

\begin{aligned} \begin{array}{rl} \Gamma & \vdash A\wedge B \\ \hline \Gamma & \vdash A \end{array} \end{aligned}

Simplification:

Given a conjoined event
Extract a constituent

Translate to symbols

"Logic"

\begin{aligned} \begin{array}{rl} \Gamma & \vdash A\wedge B \\ \hline \Gamma & \vdash B \end{array} \end{aligned}

\begin{aligned} \begin{array}{rl} \Gamma & \vdash a:A \\ \Gamma &\vdash b:B \\ \hline \Gamma & \vdash (a,b):A\times B \end{array} \end{aligned}

Mid Point: make it data

Pair:

context \(\Gamma\) (also ctx) says data \(a\) of type \(A\) and \(b\) of type \(B\);
Make a single paired datum.

\begin{aligned} \begin{array}{rl} \Gamma & \vdash x:A\times B \\ \hline \Gamma & \vdash \pi_A(x):A \end{array} \end{aligned}

Projection:

Given a paired datum
Extract a constituent

Get paid more...

\begin{aligned} \begin{array}{rl} \Gamma & \vdash A,B:Type\\\hline \Gamma & \vdash A\times B:Type \end{array} \end{aligned}

Formation

Introduction

\begin{aligned} \begin{array}{rl} \Gamma & \vdash x:A\times B \\ \hline \Gamma & \vdash \pi_B(x):B \end{array} \end{aligned}

Elimination

\begin{aligned} \begin{array}{rl} \Gamma & \vdash a:A \\ \Gamma&\vdash b:B \\ \hline \Gamma & \vdash \pi_A(a,b)=a \end{array} \end{aligned}

Computation

\begin{aligned} \begin{array}{rl} \Gamma & \vdash a:A \\ \Gamma&\vdash b:B \\ \hline \Gamma & \vdash \pi_A(a,b)=b \end{array} \end{aligned}

Final Point: make it code

\begin{aligned} \begin{array}{rl} \Gamma & \vdash A,B:Type\\\hline \Gamma & \vdash A\times B:Type \end{array} \end{aligned}

Formation

import ctx;

class Pair<A,B> {
  ...
}

Keyword for "formation"

Parameters to formation rule

Text version of \(\times\) and prefix notation because of language rules.

Context = "import packages"

\begin{aligned} \begin{array}{rl} \Gamma & \vdash a:A \\ \Gamma &\vdash b:B \\ \hline \Gamma & \vdash (a,b):A\times B \end{array} \end{aligned}

Final Point: make it code

\begin{aligned} \begin{array}{rl} \Gamma & \vdash A,B:Type\\\hline \Gamma & \vdash A\times B:Type \end{array} \end{aligned}

Formation

Introduction

class Pair<A,B> {
  Pair(A a, B b) { ... }
}

Method with no return type signals "Introduction"

I.e. making new data somewhere

Will invoke this with

new Pair(...)

Parameters to introduction rule

\begin{aligned} \begin{array}{rl} \Gamma & \vdash a:A \\ \Gamma &\vdash b:B \\ \hline \Gamma & \vdash (a,b):A\times B \end{array} \end{aligned}

Final Point: make it code

\begin{aligned} \begin{array}{rl} \Gamma & \vdash A,B:Type\\\hline \Gamma & \vdash A\times B:Type \end{array} \end{aligned}

Formation

Introduction

class Pair<A,B> {
  Pair(A a, B b) { ... }
    
  A piA() { ... }
  B piB() { ... }
}

Elimination for B.

Elimination for A

\begin{aligned} \begin{array}{rl} \Gamma & \vdash x:A\times B \\ \hline \Gamma & \vdash \pi_A(x):A \end{array} \end{aligned}

\begin{aligned} \begin{array}{rl} \Gamma & \vdash x:A\times B \\ \hline \Gamma & \vdash \pi_B(x):B \end{array} \end{aligned}

Elimination

\begin{aligned} \begin{array}{rl} \Gamma & \vdash a:A \\ \Gamma &\vdash b:B \\ \hline \Gamma & \vdash (a,b):A\times B \end{array} \end{aligned}

Final Point: make it code

\begin{aligned} \begin{array}{rl} \Gamma & \vdash A,B:Type\\\hline \Gamma & \vdash A\times B:Type \end{array} \end{aligned}

Formation

Introduction

class Pair<A,B> {
  A myA; B myB;
  Pair(A a, B b) {
    myA = A; myB=b;
  }
    
  A piA() { return myA; }
  B piB() { return myB; }
}

Retrieve b from storage when asked

Internally store a.

\begin{aligned} \begin{array}{rl} \Gamma & \vdash x:A\times B \\ \hline \Gamma & \vdash \pi_A(x):A \end{array} \end{aligned}

\begin{aligned} \begin{array}{rl} \Gamma & \vdash x:A\times B \\ \hline \Gamma & \vdash \pi_B(x):B \end{array} \end{aligned}

Elimination

\begin{aligned} \begin{array}{rl} \Gamma & \vdash a:A \\ \Gamma&\vdash b:B \\ \hline \Gamma & \vdash \pi_A(a,b)=a \end{array} \end{aligned}

Computation

\begin{aligned} \begin{array}{rl} \Gamma & \vdash a:A \\ \Gamma&\vdash b:B \\ \hline \Gamma & \vdash \pi_A(a,b)=b \end{array} \end{aligned}

TRY IT YOURSELF!

Try this right now in

Java
Scala
Haskell

(All you need is a web browser.)

class Pair<A,B> {
  A a;  B b;
  Pair(A a, B b) { 
    this.a = a; 
    this.b = b;
  }
  
  A piA() { return a; }
  B piB() { return b; }
}

public class TrialRun {
  // A way to try the code out
  public static void main(String args[]) {
    Pair<String,Integer> p = new Pair("5",5);
    System.out.println("Type " + p.piA().getClass());
    System.out.println("Type " + p.piB().getClass());
  }
}

Try it! (Java Edition)

Visit https://www.jdoodle.com/online-java-compiler/

Or us VS Code with your personal Java install

class Pair[A,B](a:A, b:B) {
  def getA():A = a
  def getB():B = b
}

val p:Pair[String,Int] = new Pair("5",5)
val a:String = p.getA()
val b:Int = p.getB()

Try it! (Scala Edition)

Visit https://scastie.scala-lang.org/

Or us VS Code with your personal Scala install

In Scala, formation and introduction can be merged together to make a concise program (but less obvious)

module Main where

data Pair a b = Pair {
  x::a,
  y::b
}

main = print (y p)
      where 
        p = Pair "5" 5

Try it! (Haskell Edition)

Visit https://replit.com/

Or us VS Code with your personal Haskall install

Haskell prefer \(\sin x\) style to \(\sin(x)\).

Pair a b means Pair(a,b);

Pair "5" 5 is Pair("5",5).

Also Haskell requires lower case for generic type names, i.e. a not A.

(y p) is Haskell for p.y

Lets Do Better

Version one of a program is the best you can do.
Version two is the best you can steal.

\begin{aligned} \begin{array}{rl} \Gamma & \vdash A \\ \Gamma &\vdash B \\ \hline \Gamma & \vdash A\wedge B \end{array} \end{aligned}

Starting Point: reasoning

Conjunction:

context \(\Gamma\) (also ctx) says events A and B hold;
Make a single combined event

\begin{aligned} \begin{array}{rl} \Gamma & \vdash A\wedge B \\ \hline \Gamma & \vdash A \end{array} \end{aligned}

Simplification:

Given a conjoined event
Extract a constituent

Translate to symbols

"Logic"

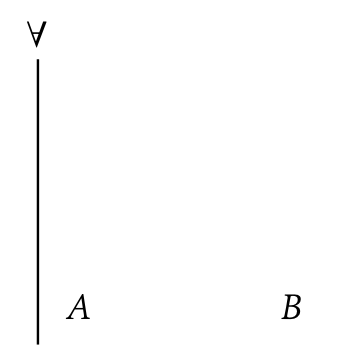
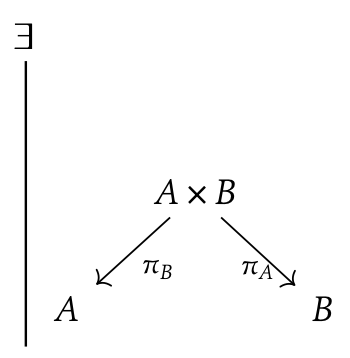
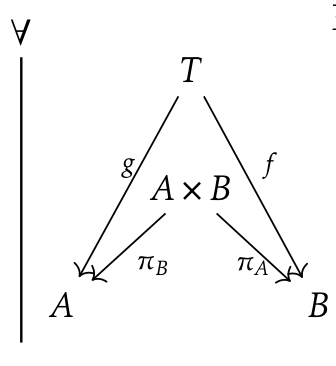
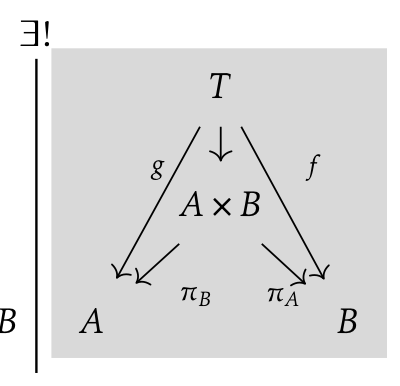
\begin{aligned} \begin{array}{rl} \Gamma & \vdash A\wedge B \\ \hline \Gamma & \vdash B \end{array} \end{aligned}

Starting Point: reasoning with reality

Sources:

context \(\Gamma\) (also ctx) says information from A and B;

Outcomes:

Combine info.
Recover individuals

Translate to flow

"Categories"

Comparison:

How would other solution look at granular scale?

Master the Competition:

Invent a translation of their's to our's.

\begin{aligned} \begin{array}{rl} \Gamma & \vdash T:Type\\ \Gamma &\vdash f:T\to A \\ \Gamma &\vdash g:T\to B \\ \Gamma & \vdash t:T\\\hline \Gamma & \vdash (f\times g)(t):A\times B \end{array} \end{aligned}

Mid Point: make it data

\begin{aligned} \begin{array}{rl} \Gamma & \vdash x:A\times B \\ \hline \Gamma & \vdash \pi_A(x):A \end{array} \end{aligned}

\begin{aligned} \begin{array}{rl} \Gamma & \vdash A,B:Type\\\hline \Gamma & \vdash A\times B:Type \end{array} \end{aligned}

Formation

Introduction

\begin{aligned} \begin{array}{rl} \Gamma & \vdash x:A\times B \\ \hline \Gamma & \vdash \pi_B(x):B \end{array} \end{aligned}

Elimination

\begin{aligned} \begin{array}{rl} \Gamma & \vdash T:Type \\ \Gamma&\vdash f:T\to A\\ \Gamma & \vdash g:T\to B \\ \Gamma & \vdash t:T\\\hline \Gamma & \vdash \pi_A((f\times g)(t))=f(t) \end{array} \end{aligned}

Computation

Final Point: make it code

\begin{aligned} \begin{array}{rl} \Gamma & \vdash x:A\times B \\ \hline \Gamma & \vdash \pi_A(x):A \end{array} \end{aligned}

\begin{aligned} \begin{array}{rl} \Gamma & \vdash A,B:Type\\\hline \Gamma & \vdash A\times B:Type \end{array} \end{aligned}

Formation

Introduction

\begin{aligned} \begin{array}{rl} \Gamma & \vdash x:A\times B \\ \hline \Gamma & \vdash \pi_B(x):B \end{array} \end{aligned}

Elimination

Computation

import ctx;

class Pair[A,B,T] (...) { 
  ...
}

import ctx;

class Pair[A,B,T](...) {
 
  def piA():A = ...
  def piB():B = ...
}

import ctx;

class Pair[A,B,T](
  t:T,
  f:T=>A,
  g:T=>B) {
 
  def piA():A = ...
  def piB():B = ...
}

import ctx;

class Pair[A,B,T](
  t:T,
  f:T=>A,
  g:T=>B) {
 
  def piA():A = f(t)
  def piB():B = g(t)
}

Quiz

Mathematics

Program

class IntMod<int n> {
  int x;
  IntMod(int a) { x = a % n; }
  int residue() { return x; }
}

\[\frac{n:\mathbb{Z}}{\mathbb{Z}/n :type} (F_{mod})\]

\[\frac{a:\mathbb{Z}}{[a]:\mathbb{Z}/n} (I_{mod})\]

\[\frac{x:\mathbb{Z}/n}{res(x):\mathbb{Z}} (E_{mod})\]

\[\frac{a:\mathbb{Z}}{ rep([a])\equiv a\pmod{n}} (C_{mod})\]

\[\frac{a:\mathbb{Z}}{prf:rep([a])<n} (C_{mod})\]

\[\frac{a:\mathbb{Z}}{prf:0\leq rep([a])} (C_{mod})\]

Mathematics:

Program

class LessThan<int n> {
  .
  .
  .
  
  
  
  
  
  
}

\[\frac{n:\mathbb{Z}}{[n] :type} (F_{<n})\]

\[\begin{array}{l} a:\mathbb{Z}, b:\mathbb{N}\\ pf:a+b+1=_{\mathbb{Z}}n\\ \hline fin(a,b):[n]\end{array} (I_{<n})\]

\[\frac{p:[n]}{rep(p):\mathbb{Z}} (E_{<n})\]

\[\frac{a:\mathbb{Z}}{ rep(fin(a,b))=a} (C_{<n})\]

class LessThan<int n> {
  // uint = unsigned int (non-negative)
  // Eq[x,y]  type of evidence for x==y
  LessThan(int a,uint b,Eq[a+b+1,n] proof){ 
    .
    .
    .

  }

}

class LessThan<int n> {

  LessThan(int a,uint b,Eq[a+b+1,n] proof){ 
    .
    .
    .


  }
  int rep() { ... }
}

class LessThan<int n> {
  int x;  // Java has no unit or "Eq" type, improvise
  LessThan(int a,int b) { 
    if (b >= 0) && ( (a+b+1) == n ) {
    	x = a;
    } else { 
      throw new IllegalArgumentException(); 
    }
  }
  int rep() { return x; }
}

Make \([n]=\{0,\ldots,n-1\}\)

Final Thoughts

Program languages (PL) add rules beyond your FIEC.
Some intro/elim rules ergonomic with idioms
- pattern matching,
- let/where clauses,
- apply/unapply,
- getters/setters,
- polymorphism by hierarchy "extends"
Some Math too subtle for average PLs.
Some Math provably undecidable (unprogrammable).

Types, Programs, & Categories

Three Steps to a Program

TRY IT YOURSELF!

Try this right now in

Java

Scala

Haskell

Lets Do Better

Quiz

Mathematics

Program

Mathematics:

Program

Make \([n]=\{0,\ldots,n-1\}\)

Final Thoughts

Turing Machine

= Universal Computer

Type Theory

= Universal Programming Language

Types & Programs

Types & Programs

James Wilson

Types, Programs, & Categories

Three Steps to a Program

TRY IT YOURSELF!

Try this right now in

Java

Scala

Haskell

Lets Do Better

Quiz

Mathematics

Program

Mathematics:

Program

Make \([n]=\{0,\ldots,n-1\}\)

Final Thoughts

Turing Machine

= Universal Computer

Type Theory

= Universal Programming Language

Types & Programs

More from James Wilson