基礎圖論
Basic Graph Theory
https://slides.com/d/mD8PiD4/live
講師介紹
- 劉哲佑
- WLCSC 25th 社長
- 高三學測生
- 劉哲佑
- WLCSC 25th 社長
- 高三學測生
TA介紹
- 李訓佑
- WLCSC 教學 x 英辯 x 模聯
- 高三學測生
- 不知道去文組還理組

What is "Graph" ?
Grid Graph ?
Grid Graph
How to present a Grid Graph ?
const int N = 1e3+5;
int Grid[N][N];Text
Text
Matrix
Traversal
-
DFS
-
BFS
DFS
void DFS(int I,int J){
// make sure (I,J) is marked visited
Output(I,J);
int nxt_i ,nxt_j;
for(int i=0;i<4;i++){
nxt_i=I+pos[i][0], nxt_j=J+pos[i][1];
// check if out of range
if(I_nxt_i_<1||nxt_i>1000||nxt_j<1||nxt_j>1000){
continue;
}
// check if visited
if(visited[nxt_i][nxt_j]) continue;
visited[nxt_i][nxt_j]=true;
DFS(nxt_i,nxt_j);
}
}DFS
Small trick
int dir[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
int cur_r ,cur_c ;
for(int i=0;i<4;i++){
int nxt_r=cur_r+ dir[i][0] ;
int nxt_c=cur_c+ dir[i][1] ;
}DFS
void DFS(int I,int J){
// make sure (I,J) is marked visited
Output(I,J);
int nxt_i ,nxt_j;
for(int i=0;i<4;i++){
nxt_i=I+pos[i][0], nxt_j=J+pos[i][1];
// check if out of range
if(I_nxt_i_<1||nxt_i>1000||nxt_j<1||nxt_j>1000) continue;
// check if visited
if(visited[nxt_i][nxt_j]) continue;
visited[nxt_i][nxt_j]=true;
DFS(nxt_i,nxt_j);
}
}BFS
while(q.size()){
I=q.front().F;
J=q.front().S;
q.pop();
for(int i=0;i<4;i++){
// next position
I__=I+pos[i][0], J__=J+pos[i][1];
if(!inRange(I__,J__)||vis[I__][J__]){
continue;
}
vis[I__][J__]=true;
Graph[I__][J__]=Graph[I][J]+1;
// count steps
q.push({I__,J__});
}
}BFS
BFS
while(q.size()){
I=q.front().F;
J=q.front().S;
q.pop();
for(int i=0;i<4;i++){
// next position
I__=I+pos[i][0], J__=J+pos[i][1];
if(!inRange(I__,J__)||vis[I__][J__]){
continue;
}
vis[I__][J__]=true;
Graph[I__][J__]=Graph[I][J]+1;
// count steps
q.push({I__,J__});
}
}BFS
#define F first
#define S second
typedef pair<int,int> pii;
queue<pii> q;
q.push( {R,C} );
while( q.size() ){ // not empty
BFS ...
}Time complexity
每個點都跑過一次
O(RC)
DFS
ZJ : b701
( ocean or land )
ZJ : a160
( 8 queen problem )
( 應該不屬於圖論但還是放上來ㄌ)
Maze BFS shortest path
ZJ : a982
ZJ : d406
ZJ : b059
(8 direction BFS )
Terms explanation
你怎麼跟別人溝通的??
A : 呀咧呀咧 今天晚上吃什麼 (歪頭
B : 大泰可嗎 wwwww
A : 唔姆.. 可
B : 走 (燦笑
vertex
edge
Text
Undirected
Directed
Text
Unweighted
9
2
1
6
10
4
4
Vertex Weight
Edge Weight
5
10
3
6
7
4
2
2
2
3
2
3
1
1
Degree
In degree
1
1
2
1
1
0
1
Out degree
2
1
0
1
2
1
0
Text
Cycle
Text
Acyclic
Grid Graph ?
- vertex weight
- cycle
- directed or undireted
How to present a Graph ?
Adjacency Matrix
-
Adjacency List
4
1
2
3
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 |
| 0 | 1 | 1 | 0 | |
| 1 | 0 | 1 | 0 | |
| 1 | 1 | 0 | 1 | |
| 0 | 0 | 1 | 0 |
Undirected
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 |
| 0 | 1 | 1 | 0 | |
| 0 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 1 | |
| 0 | 0 | 0 | 0 |
4
1
2
3
Directed
4
1
2
3
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 |
| 0 | 5 | 3 | 0 | |
| 5 | 0 | 7 | 0 | |
| 3 | 7 | 0 | 6 | |
| 0 | 0 | 6 | 0 |
Undirected + Weighted
5
7
3
6
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 |
| 0 | 5 | 3 | 0 | |
| 0 | 0 | 0 | 0 | |
| 0 | 7 | 0 | 6 | |
| 0 | 0 | 0 | 0 |
4
1
2
3
5
7
3
6
Directed + Weighted
Adj Matrix
int G[N][N];
int u ,v ;
while(m--){
// undirected
cin>>u>>v;
G[u][v]=1 ;
G[v][u]=1 ;
}Undirected
Adj Matrix
int G[N][N];
int u ,v , wt;
while(m--){
// undirected
cin>>u>>v>>wt;
G[u][v]=wt ;
// G[v][u]=wt ; directed
}Weighted
Space Complexity
V : 最大節點數量
O (V^2)
Adjacency List
STL vector

4
1
2
3
| 1 | |
|---|---|
| 2 | |
| 3 | |
| 4 |
Undirected
| 2 3 | |
|---|---|
| 1 3 | |
| 1 2 4 | |
| 3 |
4
1
2
3
Directed
| 1 | |
|---|---|
| 2 | |
| 3 | |
| 4 |
| 2 3 | |
|---|---|
| 2 4 | |
4
1
2
3
Undirected + Weighted
5
7
3
6
| 1 | |
|---|---|
| 2 | |
| 3 | |
| 4 |
| (2,5) (3,3) | |
|---|---|
| (1,5) (3,7) | |
| (1,3) (2,7) (4,6) | |
| (3,6) |
4
1
2
3
5
7
3
6
Directed + Weighted
| 1 | |
|---|---|
| 2 | |
| 3 | |
| 4 |
| (2,5) (3,3) | |
|---|---|
| (2,7) (4,6) | |
Adj List
vector<int> Graph[N];
inline void Add_vertex_undirected(int a,int b){
// Undirected graph
Graph[a].push_back(b);
Graph[b].push_back(a);
}Undirected
Adj List
vector<pair<int,int> > Graph[N];
void Add_vertex_ditected(int v,int u,int e){
// edge
// v---------> u
// vertex v to u with edge= e
Graph[v].push_back({u,e});
}Weighted
Adj List
const int MAX_N = 1e5+5;
vector<int> G1[MAX_N];
vector<vector<int> > G2(MAX_N);vector initialize
Space Complexity
V : 最大節點數量
O (V)
Adj Matrix / List
ZJ : f668
Traversal
-
DFS
-
BFS
1
3
2
4
7
6
8
5
DFS
1
3
2
4
7
6
8
5
DFS
DFS
void DFS(int root){
// make sure mark root visited
// output in DFS order (preorder)
cout<<root<<' ';
for(auto i:Graph[root]){
if(visited[i] ) continue;
visited[i]=true;
DFS(i);
}
}Exercise
ZJ : a290
1
3
2
4
7
6
8
5
BFS
1
3
2
4
7
6
8
5
BFS
BFS
queue<int> q;
visited[root]=true;
q.push(root);
while(q.size()){
int cur_node=q.front();
q.pop();
// output in BFS order
cout<< cur_node<<' ';
for(auto i:Graph[cur_node]){
if(visited[i]) continue;
visited[i]=true;
q.push(i);
}
}Exercise
ZJ : d908
ZJ : c812
Bipartite Graph
二分圖
給一個n個節點的圖
用兩個顏色將所有頂點畫過
並且使相鄰頂點顏色不相同
是二分圖嗎 ?
4
1
2
3
Draw different color
4
1
2
3
ERROR
How to draw ?
-
DFS
-
BFS
1
2
4
3
DFS
DFS
vector<int> mark(n,-1);
bool flag=true;
for(int i=0;i<n && flag;i++){
if(mark[i]!=-1) continue;
mark[i]=0;
stack<int> stk;
stk.push(i);
while(stk.size() ){
int u=stk.top();
stk.pop();
for(const int v:G[u]){
if(mark[v]==-1){
stk.push(v);
mark[v]=!mark[u];
}
else if(mark[u]==mark[v]){
flag=false;
break;
}
}
}
}DFS
vector<int> mark(n,-1);
bool flag=true;
for(int i=0;i<n && flag;i++){
if(mark[i]!=-1) continue;
mark[i]=0;
stack<int> stk;
stk.push(i);
while(stk.size() ){
int u=stk.top();
stk.pop();
for(const int v:G[u]){
if(mark[v]==-1){
stk.push(v);
mark[v]=!mark[u];
}
else if(mark[u]==mark[v]){
flag=false;
break;
}
}
}
}1
2
4
3
BFS
BFS
vector<int> mark(n,-1);
for(int i=0;i<n && flag ;i++){
if(mark[i]==-1 ){
queue<int> q;
q.push(i);
mark[i]=0;
while(q.size() && flag){
u=q.front();
q.pop();
for(auto v:G[u]){
if(mark[v]==mark[u]){
flag =false;
break;
}
else if(mark[v]==-1){
q.push(v);
mark[v]=!mark[u];
}
}
}
}
}BFS
vector<int> mark(n,-1);
for(int i=0;i<n && flag ;i++){
if(mark[i]==-1 ){
...
}BFS
if(mark[i]==-1){
queue<int> q;
q.push(i);
mark[i]=0;
... BFS
}
BFS
while(q.size() && flag){
u=q.front();
q.pop();
for(auto v:G[u]){
if(mark[v]==mark[u]){
flag =false;
break;
}
else if(mark[v]==-1){
q.push(v);
mark[v]=!mark[u];
}
}
}Exercise
Tcirc : d100
Tree ?
Is tree a graph ?
Tree ?
1
3
2
4
7
6
8
5
Tree ?
1
2
3
4
5
6
7
8
Tree ?
3
2
4
7
6
8
5
1
3
2
4
5
1
Tree ?
Forest
7
6
8
Tree
-
Connected
-
Acyclic
DAG
-
Directed
-
Acyclic
-
Graph
DAG
-
Directed
-
Tree
Topological Sort
-
先到B再到C
-
先到A再到B
A→B→C
Topological Sort
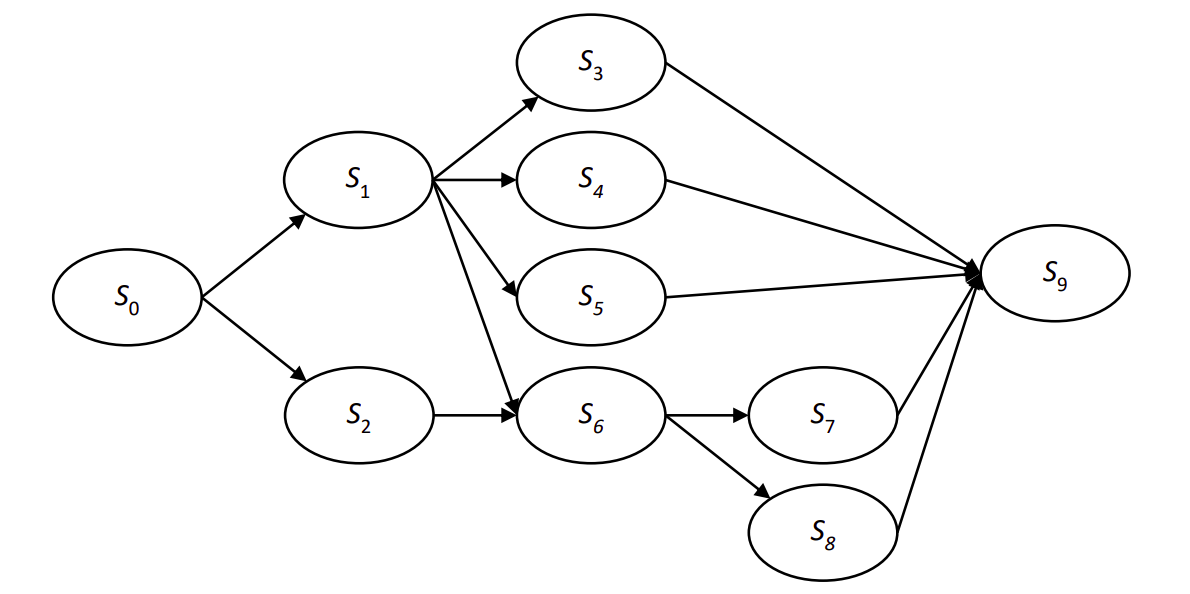
Topological Sort
-
out degree
-
in degree

In degree
0
1
1
1
1
1
2
1
1
5

Indeg = 0
Root ?

In degree
0
1
1
1
1
1
2
1
1
5

0
1
1
1
1
1
2
1
1
5
Que :
S0
Cur :
S0
Order :
S0
S1
S2
0
0
S1
S2
S3
S4
S5
S6
S3
0
S3
S9
S1
S1
S2
S4
0
S4
拓樸排序
vector<int> G[MAX_N];
int indeg[MAX_N]={};
while(m--){
cin>>u>>v;
G[u].PB(v);
indeg[v]++;
}拓樸排序
queue<int> q;
for(int i=1;i<=n;i++){
if(!indeg[i]) q.push(i);
}拓樸排序
vector<int> order;
while(q.size()){
u=q.front();
order.PB(u);
q.pop();
for(int v:G[u]){
if(--indeg[v]==0 ) {
q.push(v);
}
}
}拓樸排序
if(n==order.size()) {
cout<<"YES\n";
for(int i:order) cout<<i<<'\n';
}
else{
cout<<"NO";
}10/21 Graph Theory
By jasonliu424
10/21 Graph Theory
- 139


