The lil' serpent who bites its own tail
-
Recursion, snakes and tail call optimization
🐍🐍🐍🐍🐍🐍🐍🐍🐍🐍🐍🐍
My with recursion
A heartbreaking yet real story

+
🐍🐍🐍🐍🐍🐍🐍🐍🐍
=
❤️

"But it is very difficult to grasp"


"to understand recursion you first need to understand recursion"
Recursion starter pack
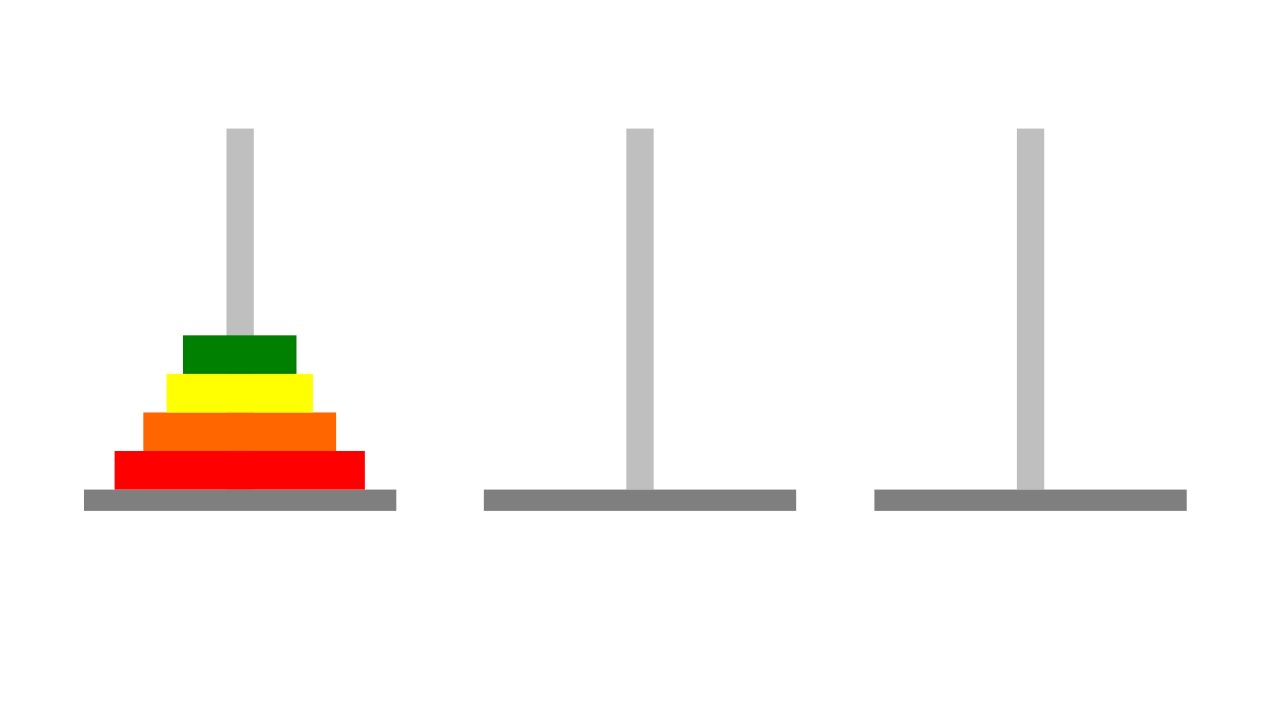
Factorial!

What is recursion anyway?
📖 "Recursion occurs when a thing is defined in terms of itself or of its type. [...] While this apparently defines an infinite number of instances , it is often done in such a way that no infinite loop occurs" 📖
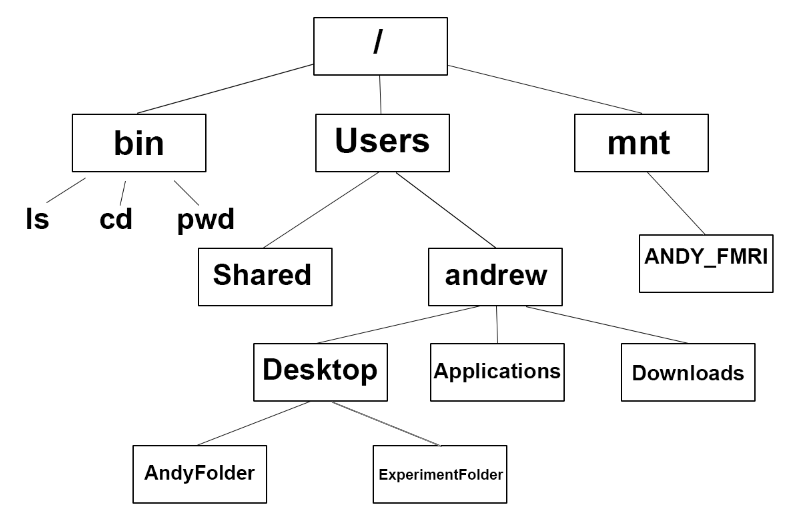
Looking for a file "example.py"
📂 /jluna
📄 InTheBeach.png.exe
📂 /Downloads
📂 /home
📄 passwrd.txt
📂 /jluna
📂 /Downloads
🐍 example.py
Binary search: Is '4' here or what?
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[0, 1, 2, 3, 4]
[3, 4]
Nope, but 4 < 5
Nope, but 4 > 2
Oh yeah!!
Types of recursion
- Simple: Single reference to itself
- Compound: Several references to itself
- Indirect: Calls a function that calls the initial function
- Anonymous: Slight variation from simple/compound but with anonymous functions
def factorial(n):
if n in {0, 1}:
return 1
return n * factorial(n-1) <---
def fib(n):
if n in {0, 1}:
return n
return fib(n-1) + fib(n-2) <-- 2x
###
def a():
b() <---
def b():
a() <---
###
def f(callable):
callable() <---Looking closely...
- Solutions to those problems that "feel more natural" are recursive. Why?
- It is the data structure that suggests a recursive algorithm or not
And which type of recursion does Python "allow me to use"?
...
def f9996():
return f9995()
def f9997():
return f9996()
def f9998():
return f9997()
def f9999():
return f9998()
f9999()😭
File "recursive.py", line 18004, in f9001
return f9000()
RecursionError: maximum recursion depth exceeded
Enter...
"The Stack"
f_a(1,2)
f_b()
f_c(42)
f_d("hello!")
The Call Stack
__main__()
def fun_a():
return "Hello!"
def fun_b():
return fun_a()
fun_b() <---__main__() -> fun_b()
__main__
def fun_a():
return "Hello!"
def fun_b(): <---
return fun_a() <---
fun_b()__main__()
└──fun_b() -> fun_a()
fun_b()
The Call Stack
__main__
def fun_a(): <---
return "Hello!" <---
def fun_b():
return fun_a()
fun_b()__main__()
└──fun_b()
└── fun_a() -> "Hello!"
fun_b()
fun_a()
The Call Stack
__main__
def fun_a():
return "Hello!"
def fun_b():
return fun_a() <--- "Hello!"
fun_b()__main__()
└──fun_b() -> "Hello!"
fun_b()
The Call Stack
__main__
def fun_a():
return "Hello!"
def fun_b():
return fun_a()
fun_b() <--- "Hello!"__main__() -> "Hello!"
The Call Stack
Stack frames
def f_a(arg1, arg2):
local_var = 3
return f_b(3, 4)Loaded variables:
arg1, arg2, local_var, f_b
Code itself
Book-keeping:
file name, row #, reference to past stack frames..
function(3, 4)
import inspect
import inspect
stack = inspect.stack()
current_frame = stack[0]
loaded_vars = current_frame.frame.f_locals
print(loaded_vars)RecursionError, a soft StackOverflow error
f_a(1,2)
f_b()
f_c(42)
f_d("hello!")
The stack has limits
Logical limit
Physical limit
f_a(1,2)
f_b()
f_c(42)
f_d("hello!")
The stack has limits
The value of the logical limit depends on the system, but is usually capped to 1000
import sys
sys.getrecursionlimit() -> 1000
sys.setrecursionlimit(100_000_000)f_a(1,2)
f_b()
f_c(42)
f_d("hello!")
RecursionError!
Logical limit
Physical limit
f_d("hello!")
Optimising tail calls 🐍
(or...not *cries recursively*)
What on earth is a tail call?
A call to a subroutine is "in the tail" if it is the last statement of a procedure
def f():
return a()
def f2(n):
if n == 1:
return a()
else:
return b()def f():
result = a()
print(result)
return result
def f2(n):
return a() + 1✅
❌
Why are they special?
- Stack frames need to be in the stack as long as they are necessary
- If calls to a function are done in the tail (last statement), we can foresee that the stack frame won't be needed anymore.
- Could we delete the stack frame then?
f_a(1,2)
f_b()
f_c(42)
f_d("hello!")
Tail Call Optimization
- Delete frames maybe not... but we can reuse them!
- That way we save on the overhead needed to create a new stack frame
a()
└─b() -> c()
a()
b()
a()
└─ c()
a()
c()
a()
a() "wtf I called b() not c()"
Let's do it then, what are we waiting for?
😀
"Cuz tracebacks from exceptions would be hella confusing then"

Tracebacks
Traceback (most recent call last):
File "illooo.py", line 10, in <module>
c()
File "illooo.py", line 8, in c
b()
File "illooo.py", line 5, in b
a()
File "illooo.py", line 2, in a
raise Exception("Obscure exception")
Exception: Obscure exceptionTraceback (most recent call last):
File "illooo.py", line 5, in <module>
a()
File "illooo.py", line 2, in a
raise Exception("Obscure exception")
Exception: Obscure exceptionCon TCO
Without TCO
Now what?
You cannot top a good ol' loop...
def fib(n):
if n in {0, 1}:
return n
return fib(n-1) + fib(n-2)def fib(n):
if n in {0, 1}:
return n
for _ in range(n):
a, b = b, a + b
return a- In imperative languages, subroutines calls cause a lot of overhead
- "For each recursive implementation there's an equivalent iterative implementation"
- If the iterative solution is easier to understand, it is preferable to use it
- If not... 🤷♂️🤷♀️
Reality check
Python is slow
Python is slow
- CPython doesn't have any type of JIT
- Tradeoff flexibility/clarity vs performance
- Just use PyPy smh
- What is slow is calling functions, not recursion itself
- Python allows to interoperate with code written in C

Although in most cases...
It is "fast enough"
Any questions?
🐍🐍🐍🐍🐍🐍🐍🐍🐍🐍🐍🐍🐍
Thankssssss for attending!
🐍
La culebrilla que se muerde la cola
By Javier Luna Molina
La culebrilla que se muerde la cola
- 421



