Криптография без односторонних функций

Проект подготовили студенты группы 0372

Жуков Владимир
Пахаревская Элина

1/35

Данная работа выполнена с использованием материалов англоязычной статьи "Secrecy without one-way functions" (Dima Grigoriev, Vladimir Shpilrain, 2013)

2/35

Содержание

Что такое односторонние функции?..................................................................4

Вычисление суммы чисел....................................................................................7

Вычисление произведения чисел....................................................................11

Схема обязательств.............................................................................................14

Сравнение двух чисел.........................................................................................17

Вычисление неоднородной функции..............................................................21

Вычисление определителя матрицы...............................................................25

Поиск узла с наибольшим секретным числом..............................................29

Поиск наибольшего числа.................................................................................32

3/35

Что такое односторонние функции?

4/35

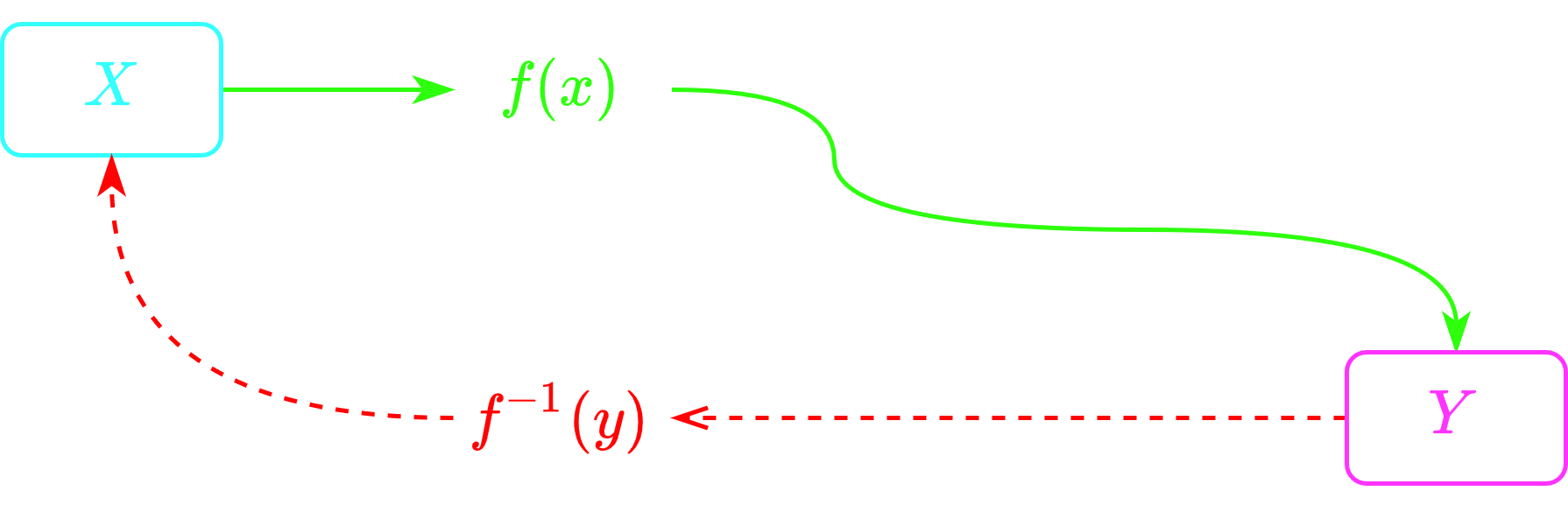
Односторонняя функция - это функция, которую довольно легко вычислить, но трудно* найти по значению функции соответствующее значение аргумента.

*Под «трудно найти» нужно понимать как: потребуется не один год расчетов с использованием ЭВМ.

Авторские протоколы:

1. вычисление суммы\(^*\)

2. вычисление произведения\(^*\)

3. сравнение двух чисел

4. вычисление неоднородной функции

5. схема обязательств

* - оптимизированные протоколы

Исследовательские протоколы:

1. вычисление определителя

2. поиск узла и наибольшим секретным числом

3. поиск наибольшего числа

5/35

Во всех описанных протоколах подразумевается следующее:

• ​все узлы находятся в широковещательной сети, причем каждый включен в замкнутую цепь \(P_1 \rightarrow P_2 \rightarrow \dots \rightarrow P_n \rightarrow P_1\) защищенных каналов связи, что необходимо для предотвращения перехвата данных
• каждый узел в точности выполняют поставленные каждому из них в протоколе задачи
• для упрощения понимания протоколов рассматриваются примеры на множестве целых чисел
• в предоставленных протоколах предполагается, что ни один узел не сообщает ложную информацию

6/35

Вычисление суммы чисел

7/35

Постановка задачи:

Вычислить сумму элементов \(n_1,n_2, \dots,n_k\), хранимых узлами \(P_1, P_2, \dots,P_k\) соответственно, не раскрывая этих значений.

Идея алгоритма:

Каждый узел прибавляет к полученному от предыдущего узла значению свое секретное число и передает результат следующему. Алгоритм начинается с первого узла, который отправляет второму случайное сгенерированное число.

8/35

Пример работы протокола

9/35

10/35

Вычисление произведения чисел

11/35

Постановка задачи:

Вычислить произведение элементов \(n_1,n_2, \dots,n_k\), хранимых узлами \(P_1, P_2, \dots,P_k\) соответственно, не раскрывая этих значений.

Идея алгоритма:

Каждый узел умножает полученное от предыдущего узла значение на свое секретное число и передает результат следующему. Алгоритм начинается с первого узла, который отправляет второму случайное сгенерированное число.

12/35

Пример работы протокола

13/35

Схема обязательств

14/35

Постановка задачи: 

Организовать такой обмен значениями между узлами, при котором гарантируются секретность и однозначность.

Идея алгоритма:

Алгоритм проходит в две фазы: передачи и раскрытия. Узлы обмениваются значениями таким образом, что к концу:

• фазы передачи никто из участников не сможет восстановить секретное число другого узла (гарантируется секретность).
• фазы раскрытия все участники будут владеть достаточной информацией, чтобы восстановить эти числа (гарантируется однозначность).

После последней фазы участники могут сравнить вычисленные значения и убедиться, что среди них нет узла, который сообщил ложную информацию.

15/35

Протокол:

1. Каждый узел раскладывает свое число на два случайных: \(n_i = r_i + s_i\). Если участники хотят работать с битами, то "0" они раскладывают или на \(0+0\) или на \(1+1\), а "1" на \(0+1\) или \(1+0\).

После этапа передачи:

\(P_1\) знает: \(s_1\), \(r_1\), \(s_2 + s_3\), \(r_1+r_2+r_3\)

\(P_2\) знает: \(s_2\), \(r_2\), \(r_1\), \(s_3\)

\(P_3\) знает: \(s_3\), \(r_3\), \(r_1+r_2\), \(s_1+s_2+s_3\)

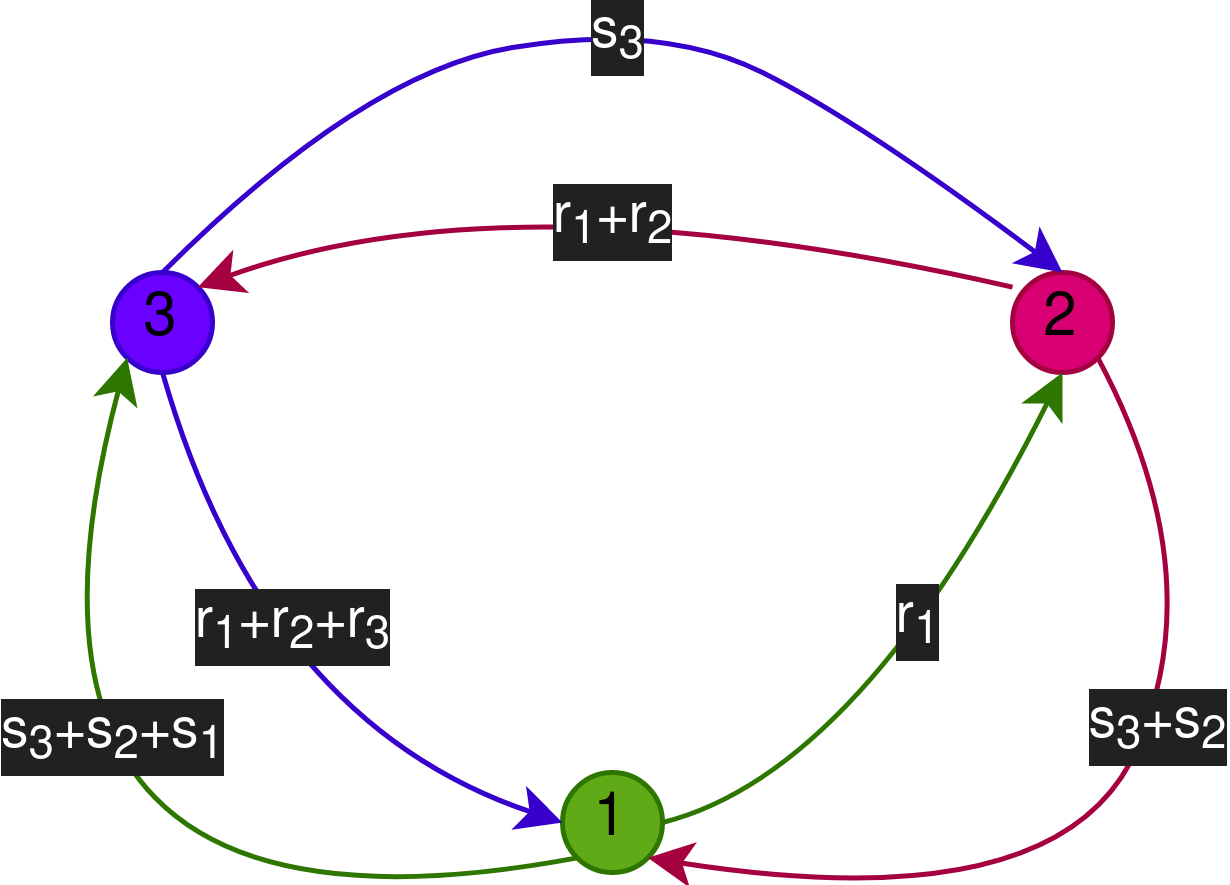
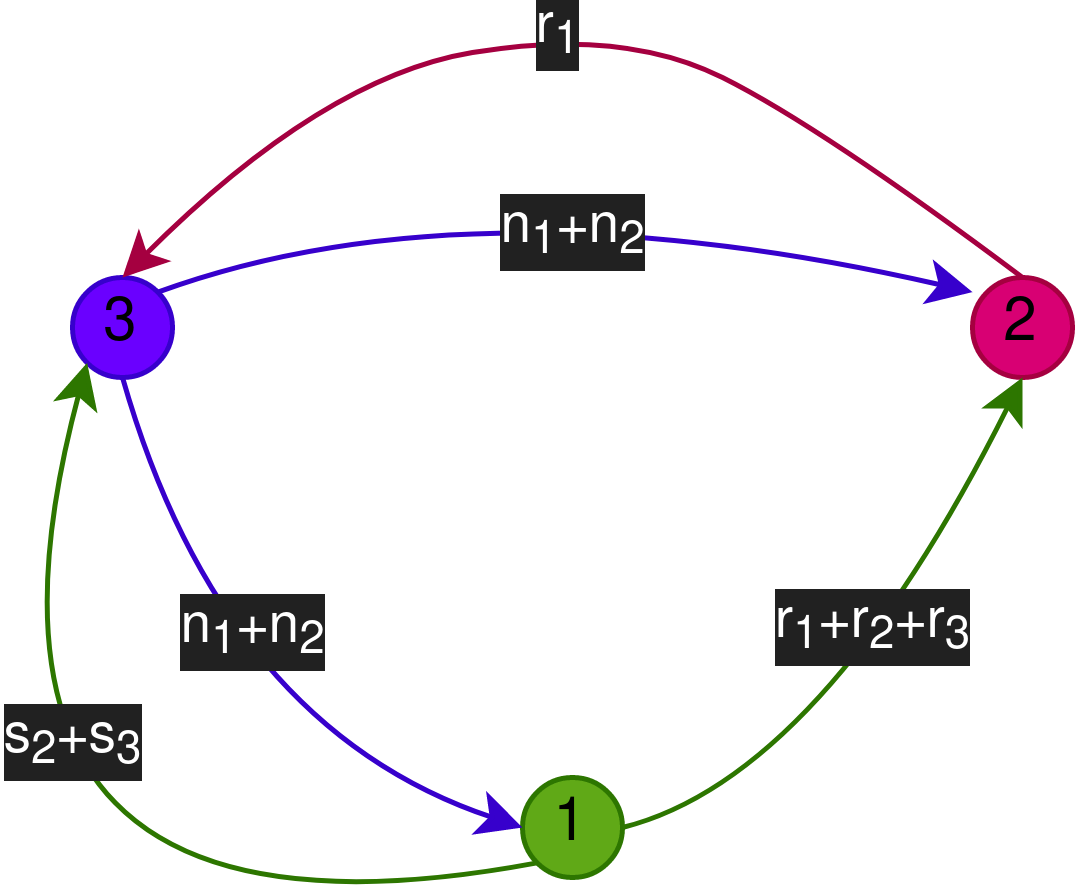
Фаза передачи

Фаза раскрытия

16/35

Сравнение двух чисел

17/35

\(n_1 \ge n_2 \Leftrightarrow n_1 - n_2 \ge 0 \\ n_{11} - n_{12} - (n_{21} - n_{22}) \ge 0 \\ n_{11} + n_{22} - (n_{21} + n_{12}) \ge 0\)

Постановка задачи:

Сравнить два числа \(n_1\) и \(n_2\), принадлежащие \(P_1\) и \(P_2\) соответственно, не раскрывая их значений.

Идея алгоритма:

Числа разбиваются на разность двух случайных чисел, после чего узлы обмениваются вторыми операндами, складывают их с первыми, и передают результаты третьему узлу. Он находит их разность и на основании следующих преобразований оценивает наибольшее число:

18/35

На видео:

• Белые числа: \(n_i\)
• Нижние числа: \(n_{i1}\)
• Верхние числа: \(n_{i2}\)

Пример работы протокола

19/35

Протокол:

1. \(P_1\) раскладывает свое число на разность \(n_1=n_{11}-n_{12}\). Затем отправляет \(n_{12}\) узлу \(P_2\).
2. \(P_2\) раскладывает свое число на разность \(n_2=n_{21}-n_{22}\). Затем отправляет \(n_{22}\) узлу \(P_1\).
3. \(P_1\) отправляет сумму \(n_{11}+n_{22}\) \(D\).
4. \(P_2\) отправляет сумму \(n_{21}+n_{12}\) \(D\).
5. \(D\) вычитает \(n_{21}+n_{12}\) из \(n_{11}+n_{22}\) чтобы получить \(n_1-n_2\) и выяснить результат.

20/35

Вычисление неоднородной функции

21/35

Постановка задачи: 

Поиск значения функции вида \(f(n_1,n_2,n_3)=n_1 \cdot n_2+g(n_3)\), где \(g\) - любая вычислимая функция.

Идея алгоритма:

Узлы вычисляют произведение первых двух секретных чисел (с помощью протокола, упомянутого ранее) и передают третьему, который находит ее сумму с функцией \(g(n_3)\).

22/35

Пример работы протокола

23/35

Протокол:

1. Узел \(P_1\) начинает процесс с отправки случайного значения \(a_0\) узлу \(P_2\)
2. \(P_2\) умножает \(a_0\) на свое \(n_2\) и отправляет результат \(P_3\)
3. \(P_3\) умножает \(a_0 \cdot n_2\) на случайный элемент \(c_0\) и отправляет результат \(P_1\)
4. \(P_1\) умножает \(a_0 \cdot n_2 \cdot c_0\) на свой \(n_1\), делит его на \(a_0\) и отправляет результат обратно \(P_3\)
5. \(P_3\) делит \(n_1 \cdot n_2 \cdot c_0\) на \(c_0\), прибавляет \(g(n_3)\) и получает искомый результат \(n_1 \cdot n_2+g(n_3)\)

24/35

Вычисление определителя матрицы

25/35

Постановка задачи: 

Необходимо найти определитель матрицы \(n\times n\), строки \(n_i\) которой распределены между \(n\) участниками сверху вниз.

Идея протокола:

Алгоритм основан на том, что при умножении матрицы на число, на него умножается и ее определитель. Каждый узел умножает хранимую строку на некоторое случайное значение, добавляет ее к полученной матрице и отправляет следующему. После этого первый узел находит определитель полученной матрицы \(n\times n\), который каждый последующий узел делит на свое сгенерированное число, получая в итоге определитель исходной матрицы.

26/35

Пример работы протокола

27/35

Протокол:

1. Узел \(P_1\) умножает \(n_1\) на случайное сгенерированное число \(m_1\), и передает результат \(P_2\)
2. Узел \(P_i\) делает то же, объединяет полученное \(n_{i - 1}\) с \(n_i\) так, чтобы получилась матрица \(i \times n\), а \(n_i\) оказалась нижней строкой, и передает результат \(P_{i+1}\)
3. Последний узел передает \(P_1\) матрицу \(n \times n\), который находит ее определитель и посылает его \(P_2\)
4. \(P_i\) делит определитель на \(m_i\) и передает следующему узлу
5. Первый узел делит принятое число на \(m_1\), получая определитель исходной матрицы, который сообщает остальным участникам, начиная со второго

\(n_i\) - секретное число узла

\(m_i\) - случайное число узла

Переменные:

28/35

Поиск узла с наибольшим секретным числом

29/35

Постановка задачи: 

Определить узел с наибольшим секретным числом так, чтобы оно не стало известно остальным.

Идея протокола:

Алгоритм основывается на том, что среднее двух чисел не превышает максимальное из этой пары. В качестве изначального среднего числа первый узел выбирает случайное число из промежутка от 1 до своего секретного, а остальные, если полученное от предыдущего узла число меньше секретного, выбирают новым средним половину их суммы, иначе полагают, что их секретное число наибольшее.

30/35

Протокол:

1. Первый узел генерирует случайное число \(N\) в промежутке \([0, n_1]\), после чего посылает его второму узлу
2. Узел \(i\) сравнивает секретное число \(n_i\) с \(N\):
   Если \(n_i = N \), то наибольшее число среди всех узлов у текущего, о чем он рассказывает остальным
   Иначе если \(n_i \gt N\), то узел \(i\) запоминает текущее \(N\) и посылает узлу \(i + 1\) число \([\frac{N + n_i}{2}]\)
   Иначе узел \(i\) посылает узлу \(i + 1\) число \(N\)

\(N\) - текущее "среднее" число

\(n_i\) - секретное число узла

Переменные:

31/35

Поиск наибольшего числа

32/35

Постановка задачи: 

Определить наибольшее секретное число так, чтобы его владелец не стал известен.

Идея протокола: 

Алгоритм основан на том, что среднее чисел может разбить их ряд на два множества: большие среднего и меньшие среднего. Для того, чтобы определить наибольшее значение, нужно "рекурсивно" искать среднее в множестве чисел, больших "текущего среднего".

33/35

Протокол:

1. Первый узел генерирует кортеж \((N, c, P)\), где \(N \in [0; n_1]\), \(c > 1\) и \(P \in \Z \backslash\{0\}\)
2. Каждый узел, начиная с первого, сравнивает свое секретное значение с \(N\):
   Если \(n_i \ge N\), то текущий узел инкрементирует счетчик и прибавляет к \(P\) свое секретное значение.
   Далее он передает кортеж следующему узлу.
3. Первый узел получает кортеж от последнего узла, после чего он вычитает свои сгенерированные числа из \(c\) и \(P\) соответственно, получая новые значения счетчика \(c'\) и суммы \(P'\).
   Если \(c' = 1\), то \(P'\) - наибольшее число и первый узел передает результат всем узлам.
   Иначе \(N =\) \(P' \over c'\) и генерируются новые значения для \(c'\) и \(P'\), как в 1 шаге. Алгоритм повторяется, начиная с 2 шага.

\(N\) - текущее среднее арифметическое

\(c\) - счетчик чисел, больших текущего среднего

\(P\) - сумма чисел, больших текущего среднего

Переменные:

\(n_i\) - секретное число \(i\)-го узла

34/35

35/35

Спасибо за внимание!