Что такое односторонние функции?

6/44

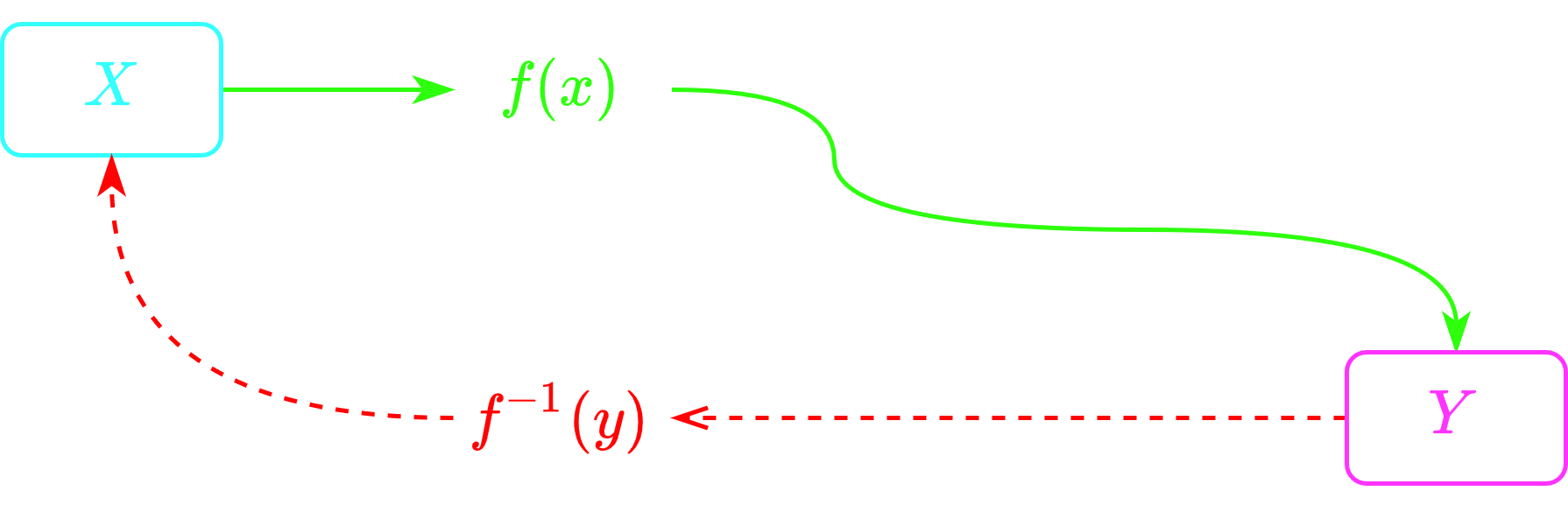
Односторонняя функция - это функция, которую довольно легко вычислить, но трудно* найти по значению функции соответствующее значение аргумента.

 

*Под «трудно найти» нужно понимать как: потребуется не один год расчетов с использованием ЭВМ.

7/44

Базовые протоколы:

1. N0 - распределение чисел

2. N1 - тасование колоды

3. N2, N2.1 - коллективная генерация числа

4. N3 - добор карт из колоды

Игры:

1. Взрывные котята

2. Уно

Множество проблем современной криптографии решается с помощью односторонних функций. Один из ярких примеров их использования – это хеш-функции. Если длина значения односторонней функции постоянна при любом аргументе, то ее называют хеш-функцией. Односторонние функции являются центральным понятием криптографии, однако само существование этих функций до сих пор не доказано, к тому же они имеют достаточно сложную реализацию. В данной работе предлагается рассмотреть некоторые криптографические протоколы и их применение в реализации карточных игр с учетом обеспечения честной игры.

8/44

Введение

Во всех описанных протоколах подразумевается следующее:

• ​все узлы находятся в широковещательной сети, причем каждый включен в замкнутую цепь \(P_1 \rightarrow P_2 \rightarrow \dots \rightarrow P_n \rightarrow P_1\) защищенных каналов связи, что необходимо для предотвращения перехвата данных
• каждый узел в точности выполняют поставленные каждому из них в протоколе задачи
• случаи, когда игроки объединяются, не учитываются

9/44

Протокол \(\mathsf{N0}\)

11/44

Цель: распределить числа от \(1\) до \(s*n\) между \(n\) игроками так, чтобы у каждого было \(s\) чисел, причем никто другой не знал какие.

Обозначения

\(P_i\) - игрок с индексом \(i\)

\(m\) - текущее число
\(s\) - количество чисел, которые получит каждый игрок

\(q_i\) - счетчик получения числа \(m\)

\(N\) - натуральное число, выбираемое участниками перед выполнением алгоритма
\(c_i\) - максимальное значение \(q_i\) (\(1 \le c_i \le N, c_i \in Z\))
\(n\) - количество игроков

12/44

Обозначения

\(P_i\) - игрок с индексом \(i\)

\(m\) - текущее число

\(q_i\) - счетчик получения числа \(m\)
\(c_i\) - максимальное значение \(q_i\) (\(1 \le c_i \le N, c_i \in Z\))

13/44

3. Описанный в пункте 2 алгоритм повторяет каждый узел до тех пор, пока у каждого участника не будет \(s\) значений (не считая \(0\)). Если у узла уже имеется \(s\) чисел, то он "пропускает ход", просто передавая полученное значение следующему узлу, пока остальные участники не доберут \(s\) чисел.

Обозначения

\(s\) - количество чисел, которые получит каждый игрок

14/44

4. Когда один из игроков забирает себе последнее значение из \(s\) возможных, он передает его далее, как будто он не забирал его себе.
5. Алгоритм прекращает свою работу, когда последнее значение из возможных \(n*s\) проходит \(N+1\) циклов.

Обозначения

\(s\) - количество чисел, которые получит каждый игрок
\(n\) - количество игроков

\(c_i\) - максимальное число раз, когда игрок получает текущее число \(m\) (\(1 \le c_i \le N, c_i \in Z\))

15/44

 Протокол \(\mathsf{N1}\)

16/44

Цель: перетасовать карты методом Кнута.

1. \(P_i\) начинает выполнение протокола, сообщая об этом остальным
2. Все игроки заводят счетчик \(q = 1\) и начинают проверять общий канал связи на наличие чисел
3. \(P_i\) выполняет протокол \(N2.1\), получая позицию карты, которую все узлы меняют с картой на позиции \(q\), увеличивая \(q\) на 1.
4. Шаг 3 выполняется игроком \(P_{i+1}\), пока \(q \neq M\).

Обозначения

\(M\) - количество карт

\(N2.1\) - протокол коллективной генерации случайного числа

17/44

Протокол \(\mathsf{N2}\)

18/44

Цель: секретно сгенерировать случайное число с помощью смежных узлов.

Обозначения

\(n\) - Количество узлов

\(n_i\) - случайно сгенерированное число узлом \(i\)

\(M\) - количество карт в колоде
\(P_i\) - узел под номером \(i\), \(i \in [1, n]\)

1. \(P_{i-1}\) и \(P_{i+1}\) тайно и независимо генерируют значения \(n_{i-1}\) и \(n_{i+1}\) по модулю числа \(M\).
2. \(P_{i-1}\) и \(P_{i+1}\) передают свои \(n_{i-1}\) и \(n_{i+1}\) узлу \(P_i\).
3. \(P_i\) складывает полученные числа и сохраняет себе сумму \(n_i = (n_{i-1} + n_{i+1}) \mod M\).

19/44

Протокол \(\mathsf{N2.1}\)

20/44

Цель: cгенерировать случайное число с помощью смежных узлов так, чтобы узел не мог сделать это нечестным образом (например, заменить его на свое).

Обозначения

\(n_i\) - случайно сгенерированное число узла \(i\)
\(n\) - количество узлов
\(M\) - количество карт в колоде

1. \(P_{i-1}\) и \(P_{i+1}\) независимо генерируют значения \(n_{i-1}\) и \(n_{i+1}\) по модулю числа \(M\).
2. \(P_{i-1}\) и \(P_{i+1}\) передают свои \(n_{i-1}\) и \(n_{i+1}\) всем узлам.
3. \(P_i\) складывает полученные числа и сохраняет себе сумму \(n_i = (n_{i-1} + n_{i+1}) \mod M\).
4. \(P_i\) передает число \(n_i\) всем узлам, которые выполняют проверку.

21/44

Протокол \(\mathsf{N3}\)

22/44

Цель: секретно взять \(k\) карт из колоды.

Обозначения

\(K\) - множество карт добора
\(M\) - количество карт в колоде \(K\)

\(N\) - множество карт сброса

\(*\) - если правила игры позволяют.

23/44

Правила

Начальные условия

• Количество игроков от двух до пяти.
• В колоде \(56\) карт, среди которых \(6\) зеленых, \(4\) черных, а остальные - нейтральные.

25/44

Процесс игры

1. В начале игры каждый игрок получает по \(1\) зеленой карте, \((6-n)\) оставшихся замешиваются в колоду (если игроков не более \(3\), то замешиваются \(2\), остальные удаляются из игры);
2. Черных карт замешивается в колоду на единицу меньше, чем игроков;

26/44

3. Каждый игрок в начале хода тянет одну карту из колоды
   • если вытянул НЕЙТРАЛЬНУЮ: помещает в колоду сброса;
   • если вытянул ЗЕЛЕНУЮ: забирает себе;
   • если вытянул ЧЕРНУЮ: проверяет наличие зеленой карты
     • если зеленая есть: черную вмешивает в колоду, а зеленую сбрасывает
     • если зеленой нет: игрок проиграл.

27/44

Обозначения:

\(n\) - количество игроков \((2 \le n \le 5)\)

\(K\) - множество карт колоды (\(\tilde K = 56\))

\(N\) - множество карт сброса

Протокол

28/44

Обозначения:

\(n\) - количество игроков

\(K\) - множество карт добора

1. Игрок-инициатор начинает игру, сообщая об этом остальным.
2. Все игроки собирают новую колоду \(K\) в зависимости от значения \(n\):

• Если \(n \ge 4\): \(\tilde K = 46 + (6 - n) + (n - 1) = 51\)
• Если \(n \le 3\): \(\tilde K = 46 + 2 + (n - 1) = 47 + n\ (\tilde K \in [49, 50])\)

Примечание: карты в колоде \(K\) располагаются в порядке: нейтральные, черные, зеленые.

29/44

3. Каждый игрок забирает одну зеленую карту без удаления ее из колоды (это выполнимо, так как в шаге 2 зеленых карт в колоде \(6 - n\)).
4. Выполняется тасование (протокол \(N1\)).
5. Игроки выбирают участника, который сделает первый ход, выбирая случайную карту с помощью протокола \(N2.1\) (карта же удаляется из \(K\)), после чего делает проверку.

Обозначения

\(n\) - количество игроков

\(K\) - множество карт добора

\(N1\) - протокол тасования

\(N2.1\) - протокол генерации случайного числа с помощью смежных узлов

30/44

После чего участник делает проверку:

• Если карта нейтральная, он помещает ее во множество \(N\)
• Если карта зеленая, он забирает ее
• Если карта черная, он проверяет наличие у себя зеленой карты:
  • Если она есть, то она помещается в \(N\), а черная возвращается на исходное место (для больше случайности можно выполнить протокол N1, но это не обязательно)
  • Если ее нет, то игрок выбывает

Обозначения

\(N\) - множество карт колоды сброса

\(N1\) - протокол тасования

31/44

Правила

Есть две колоды "прикуп" и "сброс". Из первой игроки выбирают карты, а во вторую - сбрасывают.

Каждая карта представлена в 4 цветах: красный, синий, желтый и зеленый.

В начале игры каждому игроку выдается по 7 карт. После этого все выбирают каким-то способом первого игрока, который сделает первый ход.

В колоде "прикуп" изначально имеется 108 карт, среди которых

1. цифровые карты от 1 до 9 в двойном количестве и по одной с цифрой 0
2. активные карты "пропусти ход", "возьми две" и "наоборот" в двойном количестве
3. черные активный карты "закажи цвет" и "закажи цвет и возьми 4 карты" по одной

33/44

Ходы передаются по часовой стрелке. Во время своего хода игрок может выложить карту по одному из следующих правил:

• карта одного цвета с последней в колоде сброса
• карта должна иметь ту же цифру
• карта должна быть активной и иметь ту же картинку
• карта должна быть черной активной

Если у игрока нет подходящей карты, то он берет одну из колоды "прикуп" и выкидывает ее если это возможно, иначе оставляет себе, а ход передается следующему игроку.

34/44

Игра продолжается до тех пор, пока кто-то из игроков не скинет все свои карты. Он и будет победителем.

Правило "Уно!"
Если после выкидывания карты у игрока остается одна и кто-то раньше него говорит "Уно", то он берет одну карту из колоды "прикуп".

35/44

Протокол

Обозначения

\(n\) - количество игроков
\(m\) - начальное число карт на руках у игрока (\(m = 7\))
\(K\) - множество карт "прикуп" (\(\tilde K = 108\))
\(N\) - множество карт "сброс"
\(Q_i\) - множество карт, имеющиеся на руках игроков
\(L_i\) - множество карт, которые игрок взять не может

36/44

1. Игрок \(P_i\) начинает игру, о чем сообщает остальным
2. Выполняются протоколы \(N0\) (для \(s = \tilde K/n\)) и \(N1\), после чего игроки берут \(m\) карт
3. Выбирается игрок \(P_i\), который делает первый ход и передает его следующему \(P_{i+1}\)

Обозначения

\(\tilde K\) - количество карт во множестве добора

\(n\) - число игроков

\(m\) - начальное число карт на руках у игрока

\(N0\) - протокол выдачи s чисел игрокам

\(N1\) - протокол тасования

37/44

4. Игрок \(P_i\) проверяет возможность выполнения хода:
   • Если такая возможность есть, то он выкидывает карту, а ход передается следующему
   • Иначе выполняется протокол \(N3\) для \(k = 1\):
     • Если после взятия карты ход возможен, он ее выкидывает и передает ход следующему игроку
     • Иначе передает ход игроку \(P_{i+1}\)

Обозначения

\(L_i\) - множество карт, которые игрок взять не может

\(N3\) - протокол добора \(k\) карт

Примечание: каждая выброшенная карта игроком \(P_i\) заносится во множество \(L_i\).

38/44

Честность

Возможные варианты лжи

1. Игрок взял не свою карту
2. Игрок выкинул не свою карту
3. Игрок заявил, что выкинутая карта другого игрока принадлежит ему

39/44

Игрок взял не свою карту

Решение

Ложь выявится в процессе игры: когда он выкинет эту карту, другой игрок заметит, что индекс этой карты принадлежит ему, о чем сообщит остальным.

40/44

Игрок выкинул не свою карту

Решение

Как только игрок выкинет не свою карту, другой игрок это заметит и сообщит остальным.

41/44

Игрок заявил, что выкинутая карта другого игрока принадлежит ему

Решение

Оба игрока сообщают свои счетчики \(q_i\) и \(q_j\), соответствующие карте и сгенерированные в процессе выполнения протоколов \(N0\) или \(N3\). У кого его не будет или он окажется больше, тот и лжет.

Если же так получилось, что эти числа равны, то игру начинают заново, потому что определение лжеца не представляется возможным.

42/44

Вариант реализации честной игры

Все действия, совершаемые игроками, на любом этапе игры и выполнении любого протокола, записываются в логи. Они позволяют согласовать состояние всей системы и обнаружить игроков, играющих нечестно.

43/44