BETS - Desenvolvimento do pacote estatístico para extração e análise de séries temporais econômicas
Trabalho de Conclusão de Curso
Jonatha Azevedo da Costa
Orientador: Prof. Dr. Jony Arrais
Imagine o seguinte problema!
PEDRO
economista
Deseja obter dados para uma análise de alguns componentes da economia do Brasil
Indicador de Incerteza da economia
Índice de confiança da indústria
Depois de obter os dados, Pedro deseja analisar os dados obtidos de acordo com uma metodologia, para fazer previsões.
- Software
- Possibilidade de carregar os dados
- Mecanismos que auxiliam na análise
- Menor custo possível
Esbarrando com mais alguns problemas:
BETS
Solução:
Brazilian Economic Times Series
O BETS é um pacote para o R, que fornece de maneira descomplicada , milhares de dados de diferentes fontes. Para utilizar, basta rodar o seguinte comando:
Para usar, basta:
install.packages("BETS")
require(BETS)
Imagem: Alguns centros de informações disponíveis.
BETSsources()The sources available at BETS, to date, are:
> Banco Central, IBGE, Sidra, FGV
Tudo bem, mas como eu obtenho esses dados de diferentes lugares através do BETS no R?
require(BETS)
#pesquisando
BETSsearch(description = "Indicador de Incerteza",lang = 'pt')
BETSsearch(description = "Confiança da industria",lang = 'pt')
#Obtendo os dados
IIEBR = BETSget(code = "ST_100.0")
confianca = BETSget(code = "4393")Simples...
| Pacotes | Metadados | Extação | Exportração | Análise |
|---|---|---|---|---|
| rbcb | OK | OK | X | X |
| ecoseries | X | OK | X | X |
| ribge | X | OK | X | X |
| BETS | OK | OK | OK | OK |
O BETS não está sozinho no que diz respeito a obtenção de dados de forma integrada ao R, existem os pacotes: rbcb, ecoseries e o ribge.
Além da integração com os dados, o BETS fornece funções que auxiliam uma análise com base na metodologia de Box & Jenkins.
A metodologia de Box & jenkins, consiste num processo de 5 passos:
- Considera-se uma classe geral de modelos: SARIMA(p,d,q)(P,D,Q);
- Identifica-se um modelo com base nas autocorrelações e autocorrelações parciais e outros critérios;
- Estima-se os parâmetros do modelo identificado;
- Verifica-se se o modelo ajustado é adequado aos dados através de uma análise de resíduos;
- Repete-se os passos anteriores até obter resultados coerentes.
Maravilha, utilizarei o R e o BETS!
Série temporal: Coleção de observações feitas sequencialmente ao longo do tempo.
Z_{t} = T_{t} + C_{t} + R_{t}.
(1)
- Tendência: indica uma mudança de longo prazo no nível médio de uma série temporal;
- Sazonalidade: está ligado à periodicidade ou ciclo geralmente em função de algum fenômeno dentro de um ano;
- Erro: ruido branco, variável aleatória com média 0 e variância constante.
Seguindo o processo de Box & Jenkins, temos:
1 - Considera-se uma classe geral de modelos: SARIMA(p,d,q)(P,D,Q)
Devemos garantir estacionariedade dos dados.
Def: uma série se diz estacionária se e somente se:
Z = \{Z_{t}, t \in T\}
E\{Z(t)\} = \mu(t) = \mu
t \in T
, para todo
E\{Z^{2}(t)\}
t \in T
, para todo
\gamma(t_{1},t_{2}) = Cov\{Z(t_{1},Z(t_{2}))\}
, é uma função de
\| t_{1} - t_{2}\|
(2)
Diferenciações, observação das FACS e testes de raiz unitária.
2 - Identifica-se um modelo com base nas autocorrelações e autocorrelações parciais e outros critérios;
- Identificar estacionáriedade;
- Identificar as ordens do modelo (parte sazonal e não sazonal).
\rho_\tau = \frac{\gamma_\tau}{\gamma_0}, \tau \in Z,
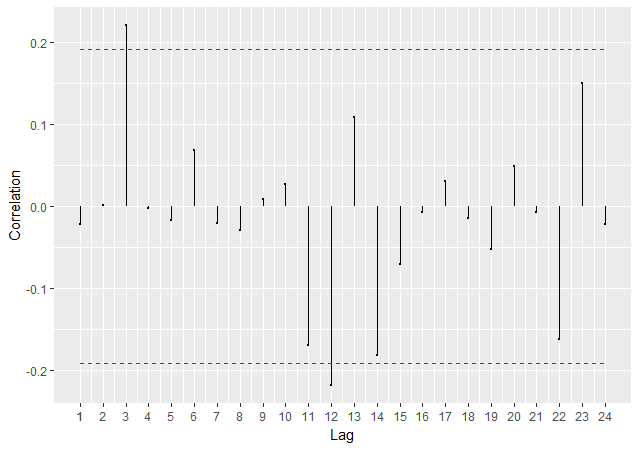
FAC:
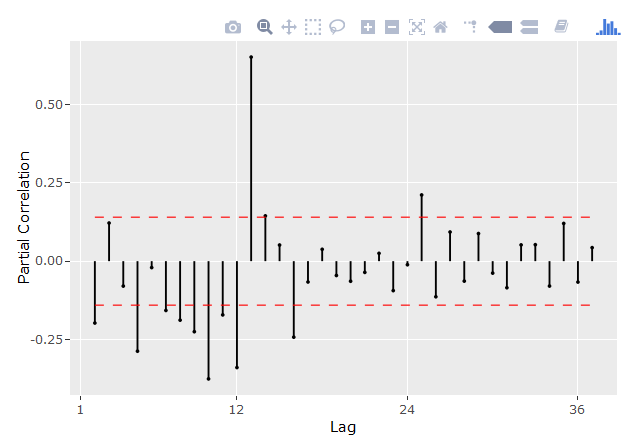
FACp:
\Phi_{kk} = Corr(X_t, X_{t-1}/X_{t-1}, X_{t-2}, \ldots, X_{t-\tau+1}).
(3)
require(BETS)
corrgram(dados,ci = 0.99, style = "normal", lag.max = 14)
corrgram(dados,ci = 0.99, style = "partial", lag.max = 36)
require(forecast)
modelo = Arima(dados, order = c(p,d,q),seazonal = c(P,D,Q) Utilizando o teste de Dickey-Fuller Aumentado, para testar a presença de estacionaridade com o auxílio da seguitne regressão:
\Delta y_t = \beta_1 + \beta_2 t + \delta y_{t-1} +
\sum\limits_{i=1}^m \alpha_i \Delta y_{t-i} + \epsilon_t,
(4)
Considerando a H_0 como:
\delta \neq 0
require(BETS)
ur_test(diff(dados))Imagem: autocorrelação
Imagem: autocorrelação parcial
3- Estima-se os parâmetros do modelo identificado
require(forecast)
modelo = ARIMA(dados,order = (3,2,2),seazonal = c(1,1,1))
require(BETS)
t_test(modelo, alpha = 0.01)A estimação dos parâmetros do modelo pode ser obtida atráves da função Arima do pacote forecast passadas a função t_test, do BETS.
Considere o modelo, por exemplo, SARIMA(3,2,2)(1,1,1)[12]
Coeffs Std.Errors t Crit.Values Rej.H0
ar1 -0.5766109 0.19482702 2.959604 2.60252 TRUE
ar2 -0.1841010 0.12135918 1.516993 2.60252 FALSE
ar3 0.2337741 0.08885427 2.630983 2.60252 TRUE
ma1 -0.7859292 0.19590612 4.011764 2.60252 TRUE
ma2 -0.2137794 0.19422081 1.100703 2.60252 FALSE
sar1 0.1025771 0.10058572 1.019798 2.60252 FALSE
sma1 -0.8794802 0.08685930 10.125342 2.60252 TRUEmodelo = ARIMA(dados,order = (3,2,1),seazonal = c(0,1,1))4 - Verifica-se se o modelo ajustado é adequado aos dados através de uma análise de resíduos;
Através do diagnóstico do modelo, fazendo uso teste de Ljung-Box, onde:
- Verifica-se a existência de autocorrelações dos resíduos;
- Assume as seguintes hipóteses:
H_0: Os resíduos são i.i.d
H_1: Os resíduos não são i.i.d
{
diag = tsdiag(modelo)- Distribuição dos resíduos padronizados;
- FAC dos resíduos;
- Dependência serial para todas as defasagens
E agora é possível realizar as previsões, utilizando , por exemplo:
modelo = ARIMA(dados,order = (3,2,1),seazonal = c(0,1,1))
forcast(modelo, h = n)
BETS::predict(modelo)Adorei!
Criação de pacotes para o R
Vignettes
data
R
man
tests
inst
src
LICENSE
DESCRIPTION
NAMESPACE
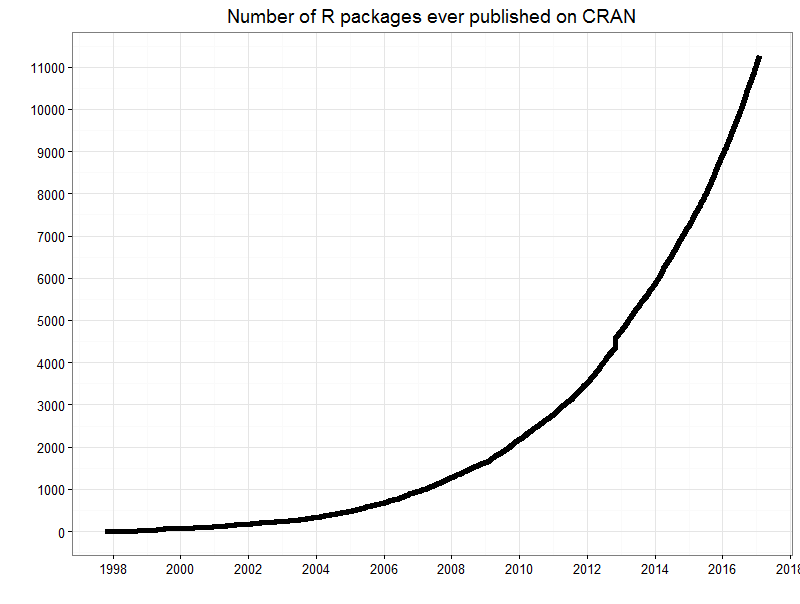
Imagem: Quantidade de pacotes ao longo dos anos.
PKG
O que será construído a seguir, é:
- Finalizar o estudo de caso onde será demonstrado com detalhes outras funcionalidades e os testes aplicados na modelagem da série escolhida;
- Listar e argumentar o alcance do pacote;
- Versões futuras do pacote.
OBRIGADO!
Apresentação - TCC
By John Azevedo
