Diagonals of Operators
John Jasper
South Dakota State University

The Pythagorean Theorem
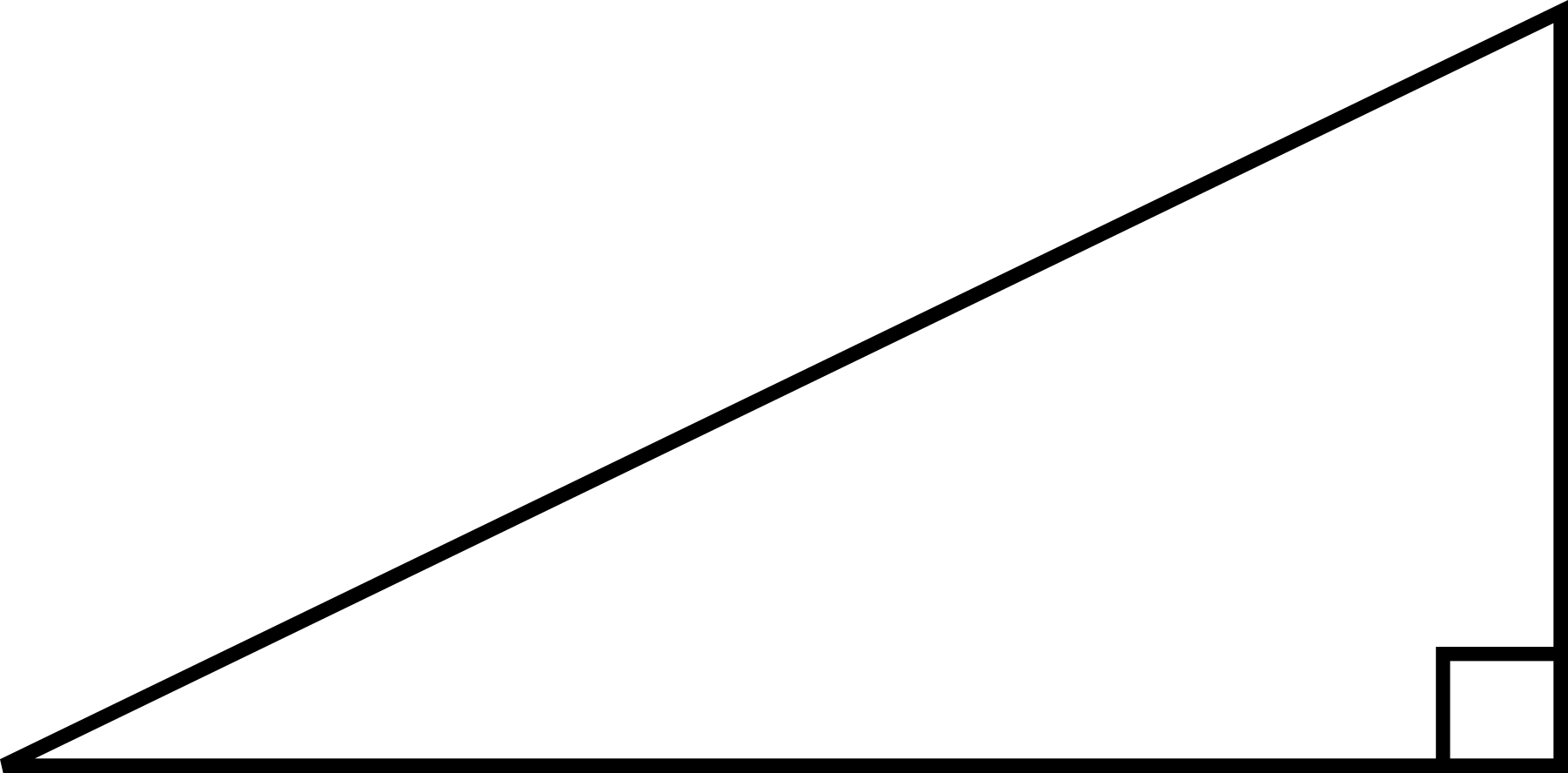
Theorem. If \(\Delta\) is a right triangle with side lengths \(c\geq b\geq a\), then \[a^{2}+b^{2}=c^{2}.\]
\(a\)
\(b\)
\(c\)
The Pythagorean Theorem
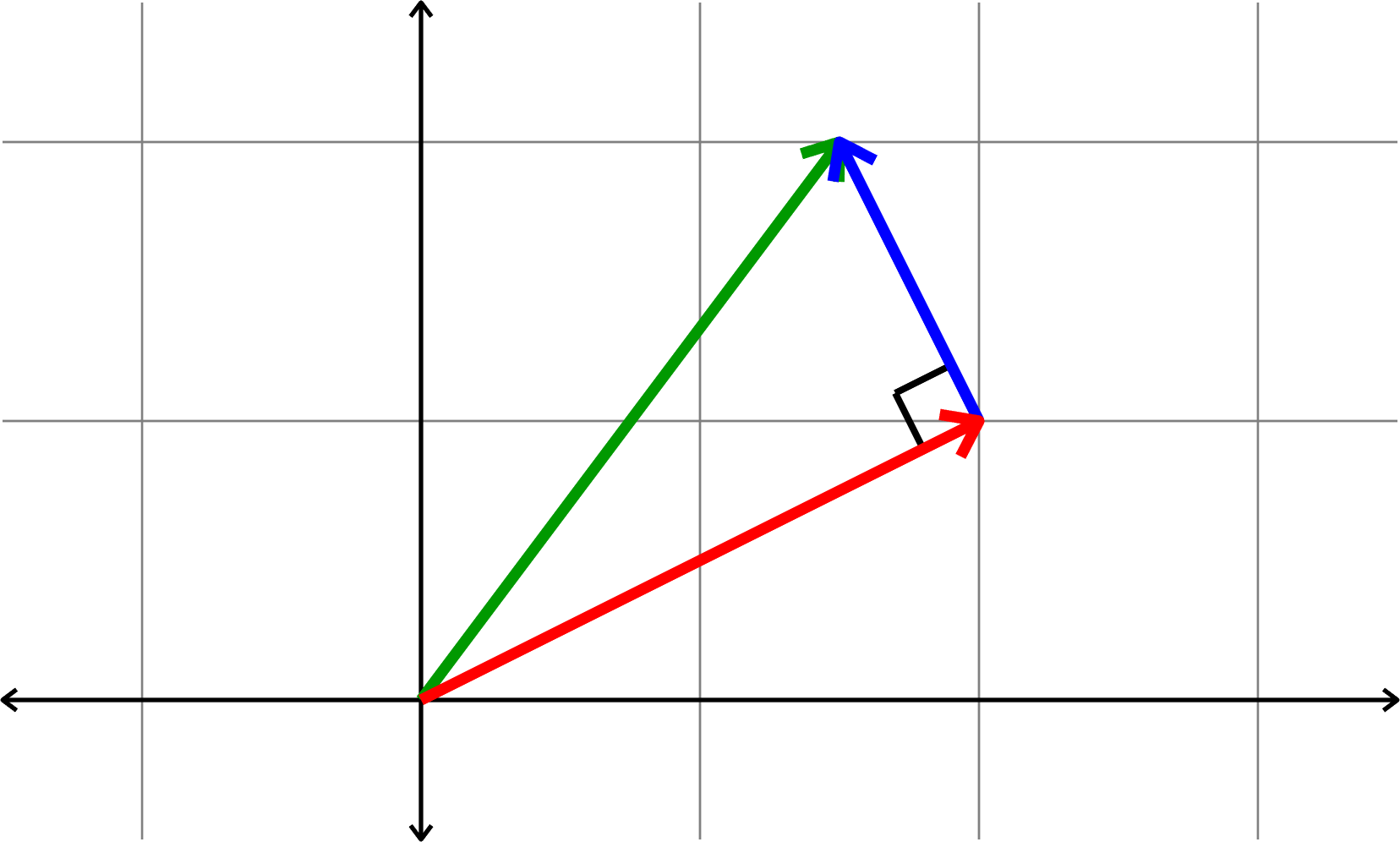
Theorem. If \(v\) and \(w\) are orthogonal vectors, then \[\|v\|^2 + \|w\|^2 = \|v+w\|^2.\]
\(v\)
\(w\)
\(v+w\)
The Pythagorean Theorem
(The Standard Generalization)
Theorem. If \(v_{1},v_{2},\ldots,v_{k}\) are pairwise orthogonal vectors, then
\[\|v_{1}\|^2 + \|v_{2}\|^2 + \cdots + \|v_{k}\|^{2} = \|v_{1}+v_{2}+\cdots+v_{k}\|^2.\]
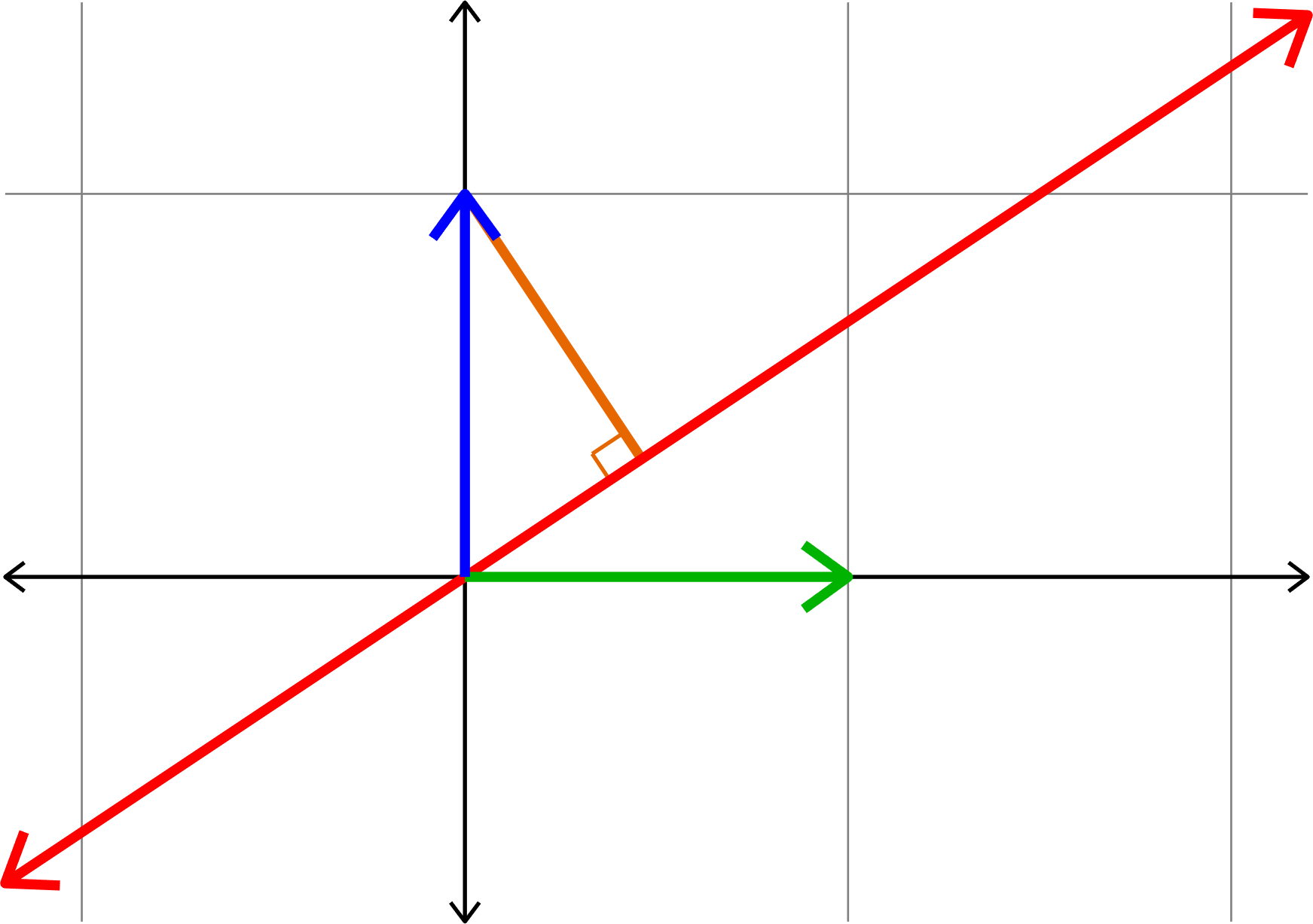
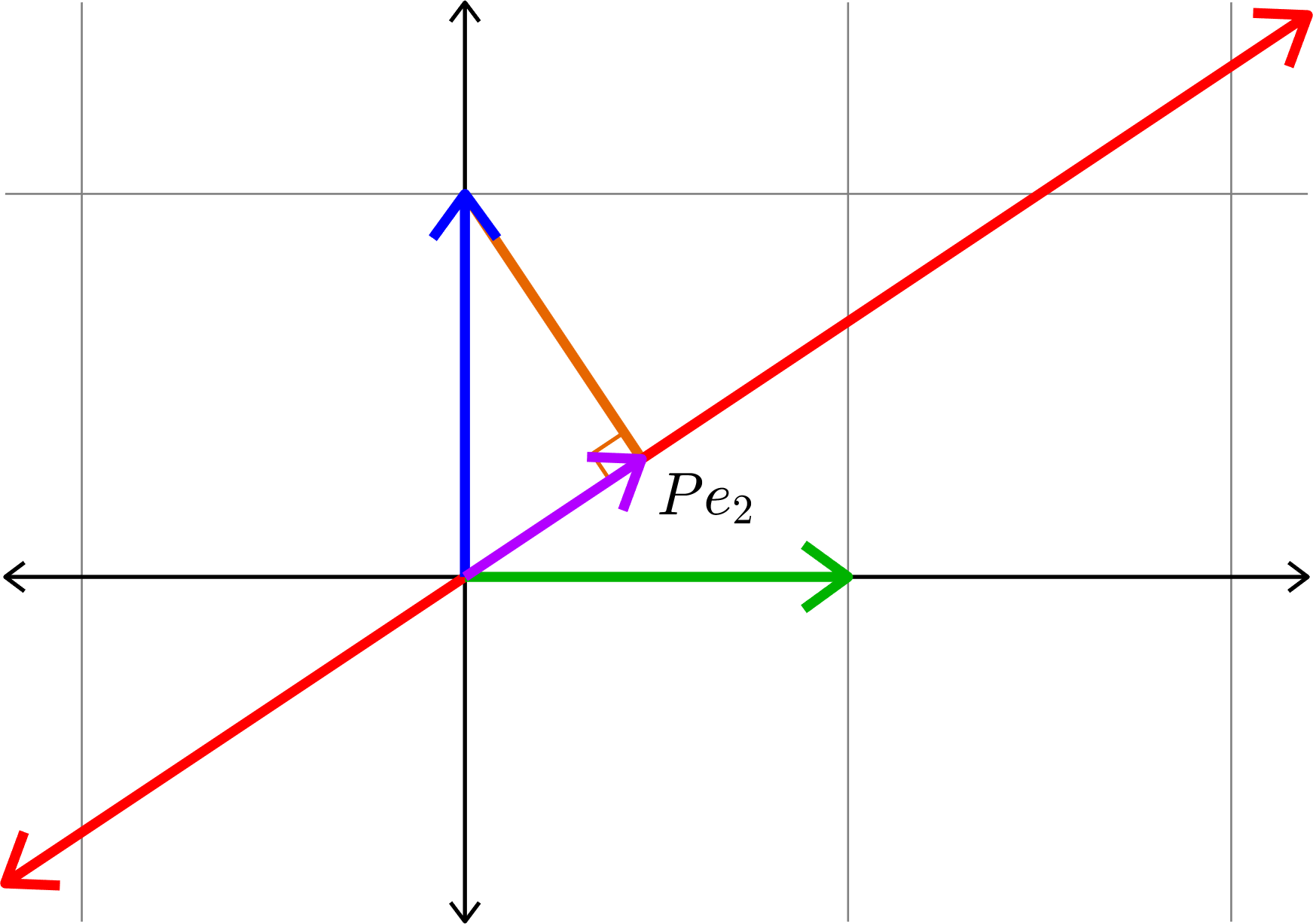
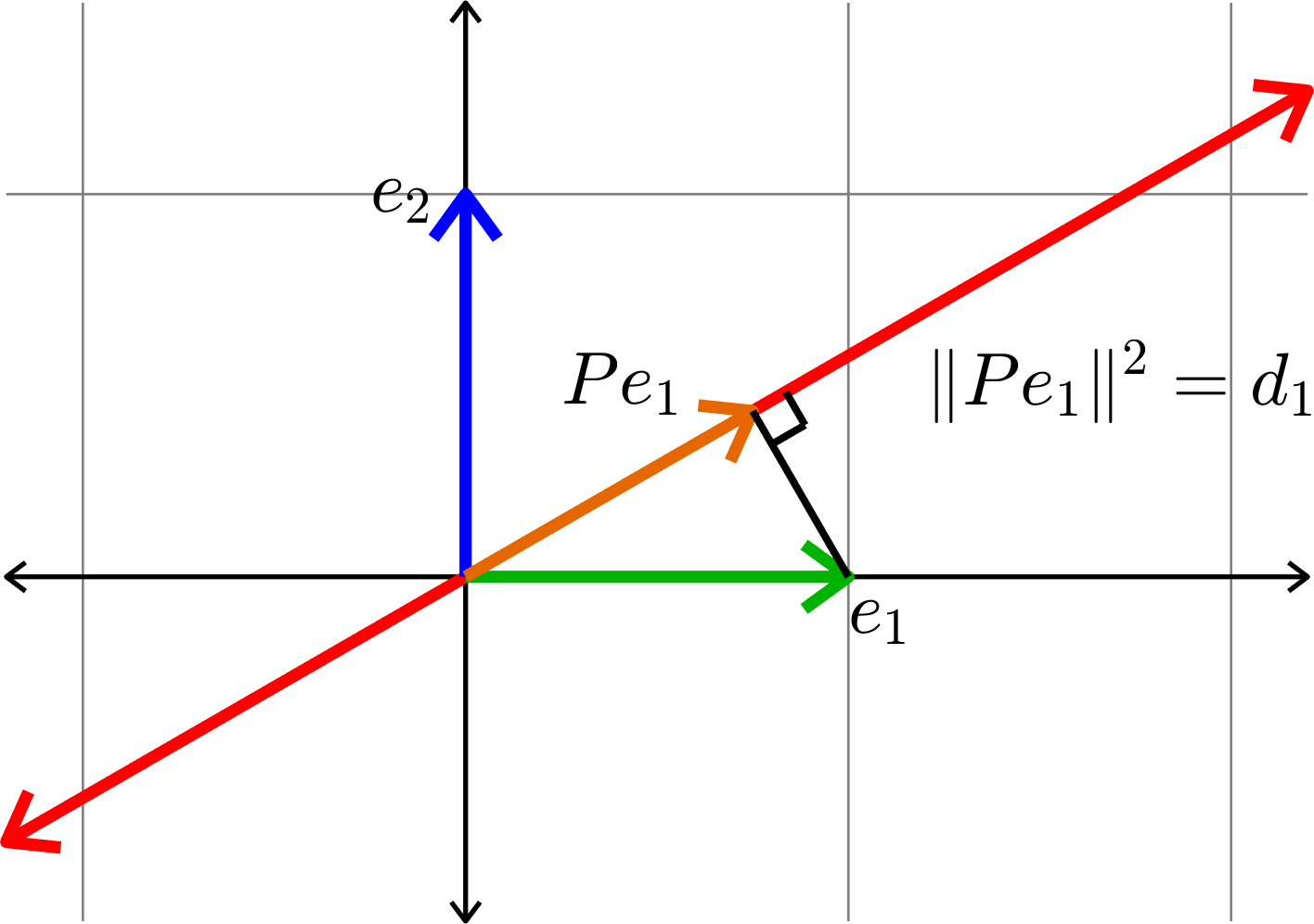
Kadison's Observation
\[\|Pe_{1}\|^{2} + \|Pe_{2}\|^{2} = 1\]
Kadison's Observation
Kadison's Observation

Kadison's Observation
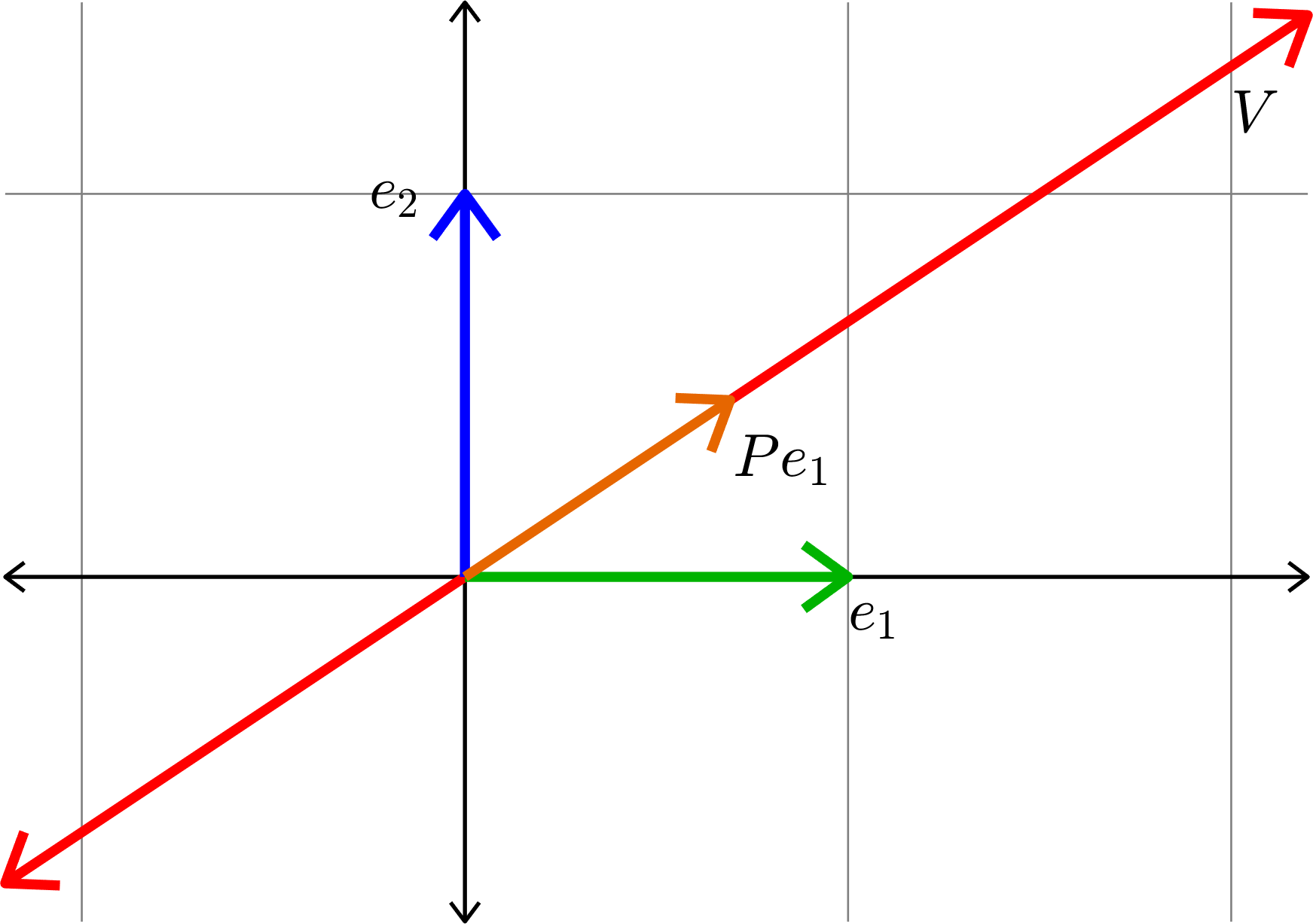
Kadison's Observation
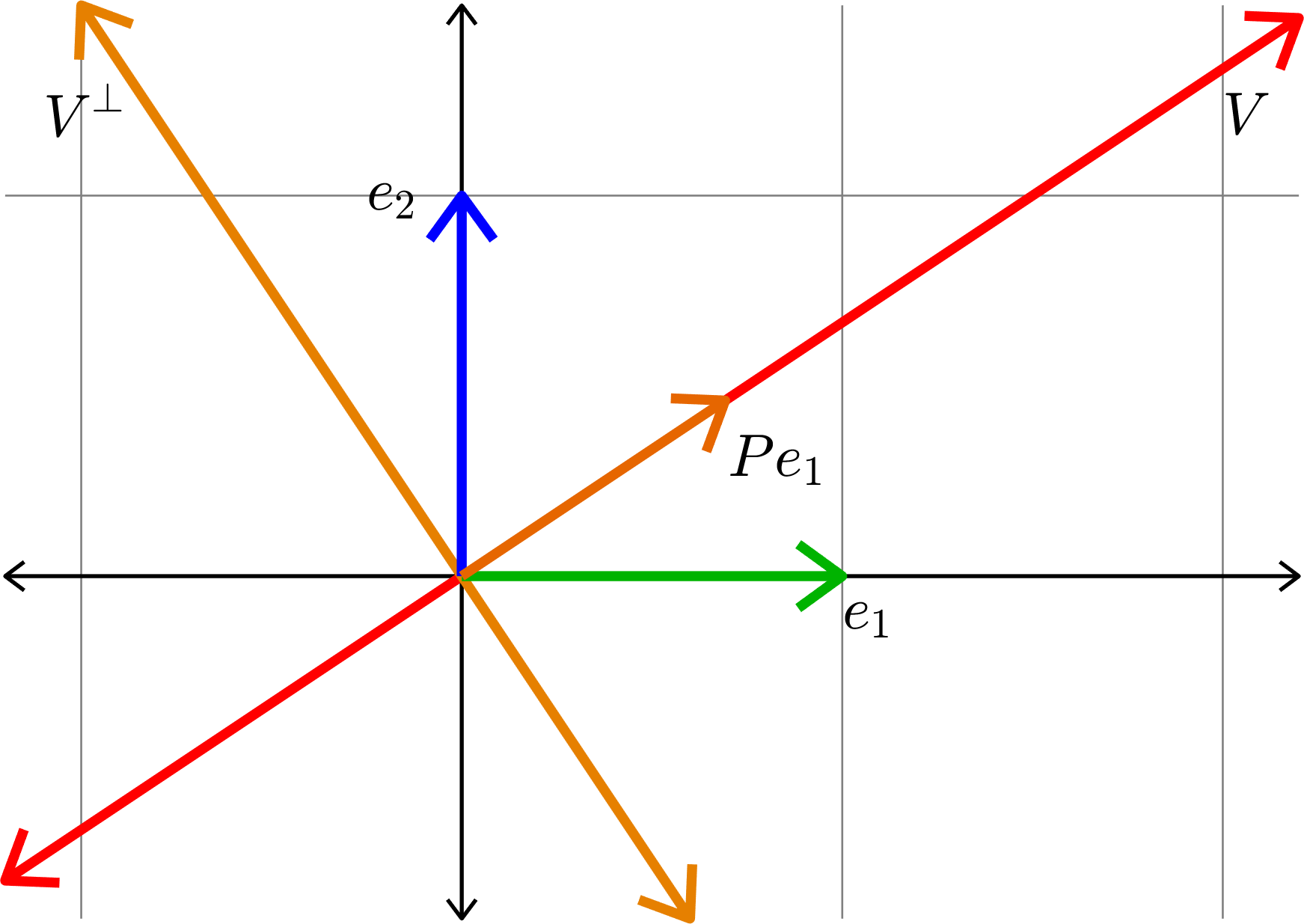
Kadison's Observation
Kadison's Observation

Kadison's Observation
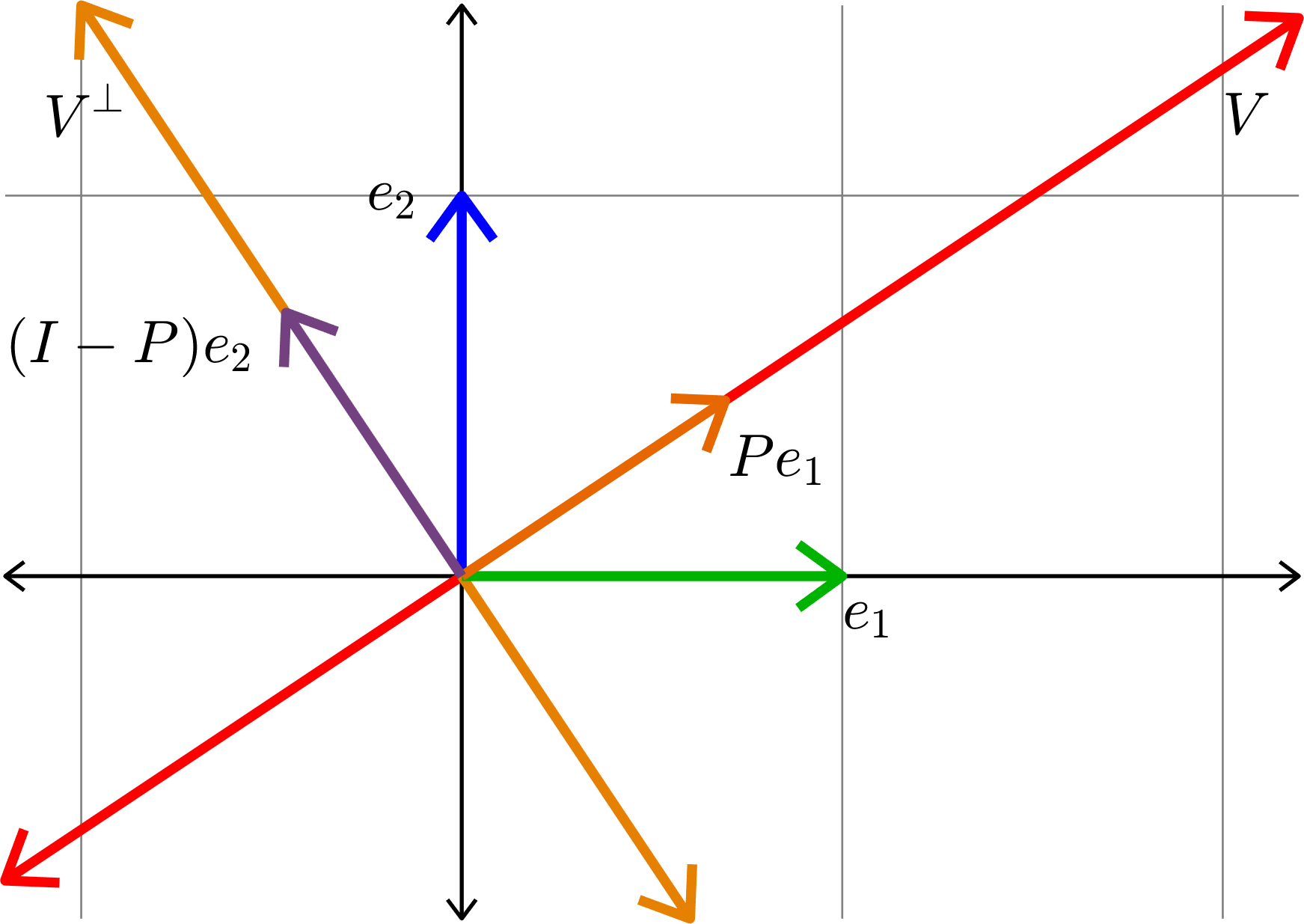
Kadison's Observation
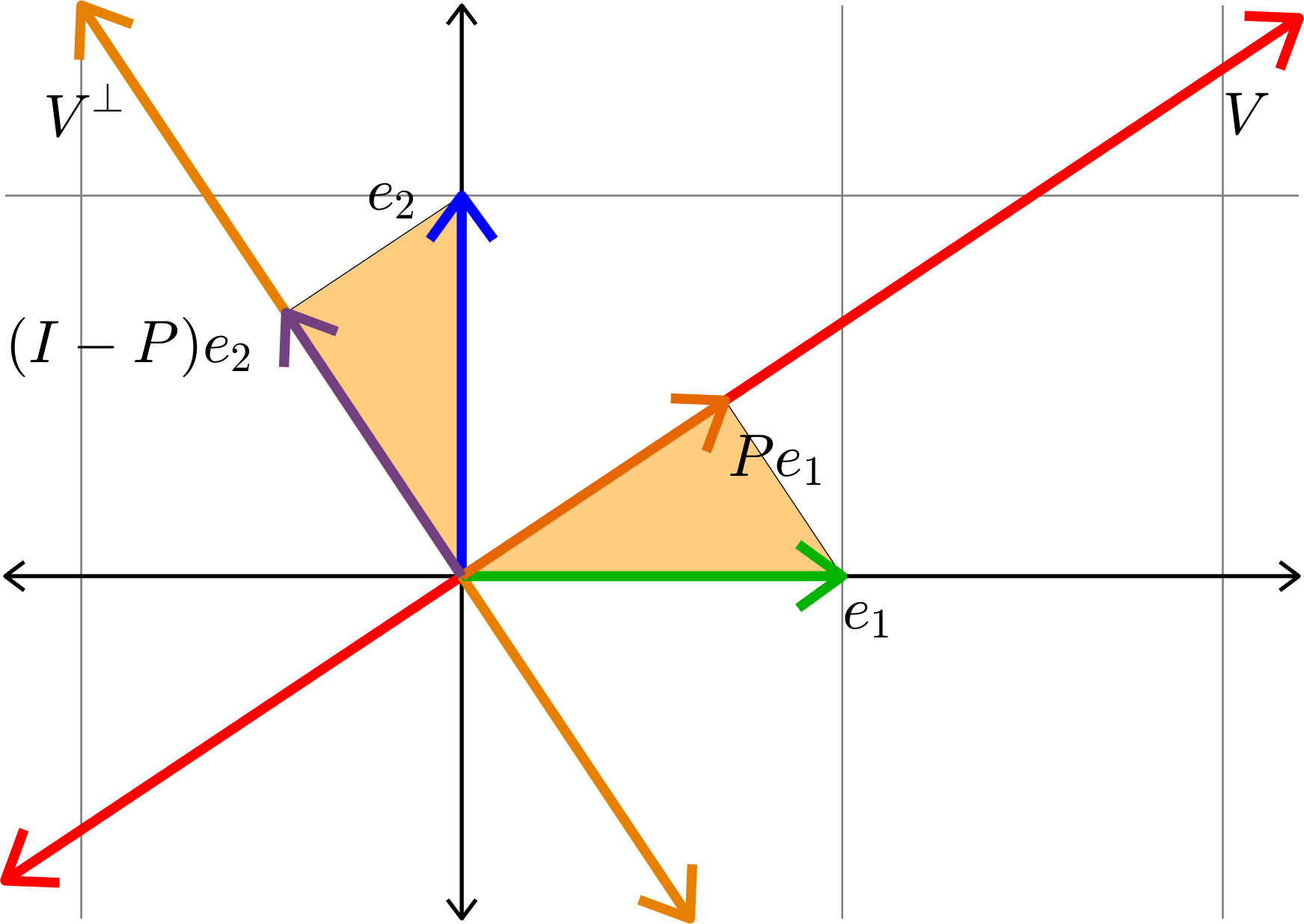
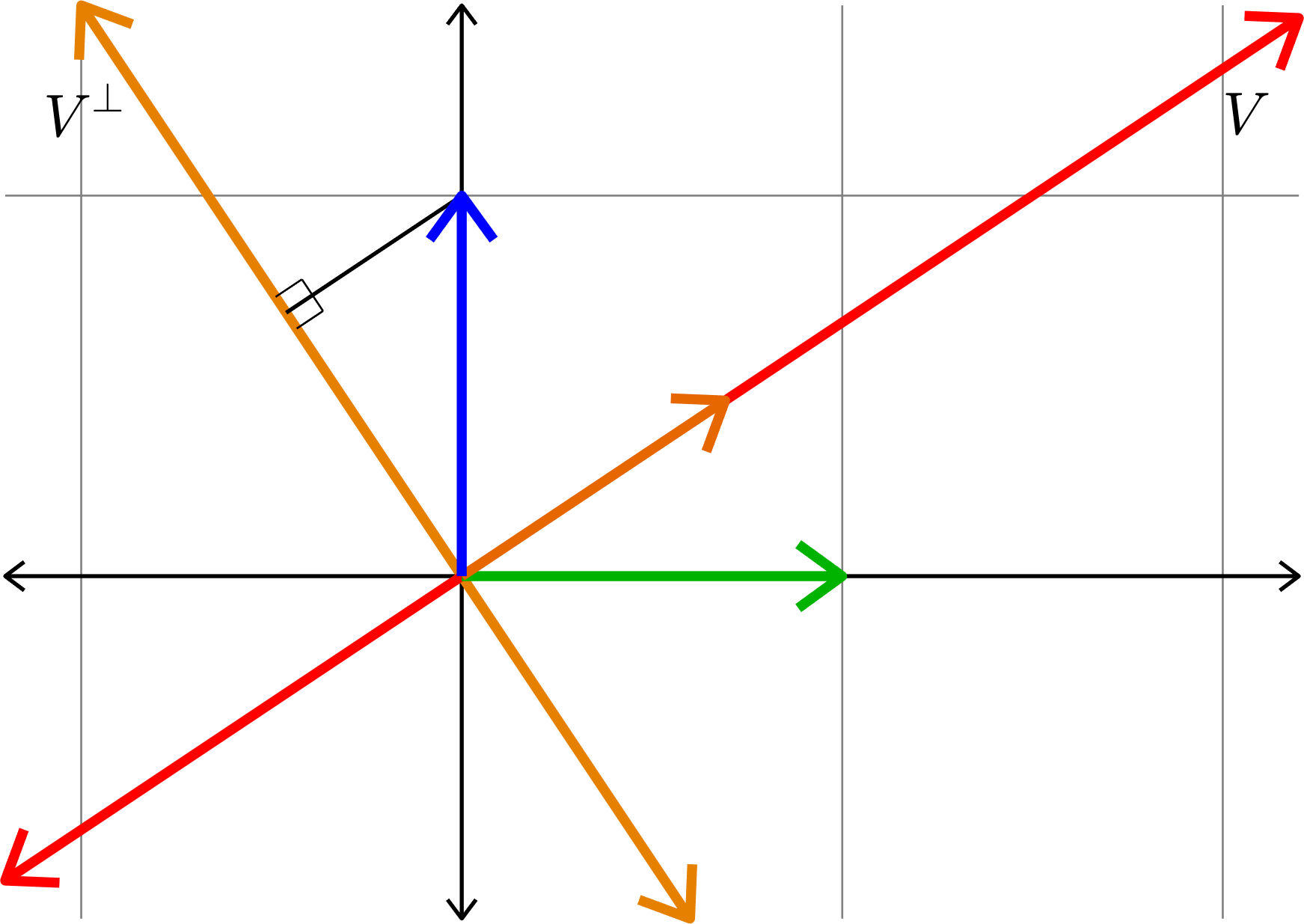
Similar Triangles!
\[\|(I-P)e_{2}\| = \|Pe_{1}\|\]
Kadison's Observation

Kadison's Observation
Kadison's Observation

Kadison's Observation
Kadison's Observation
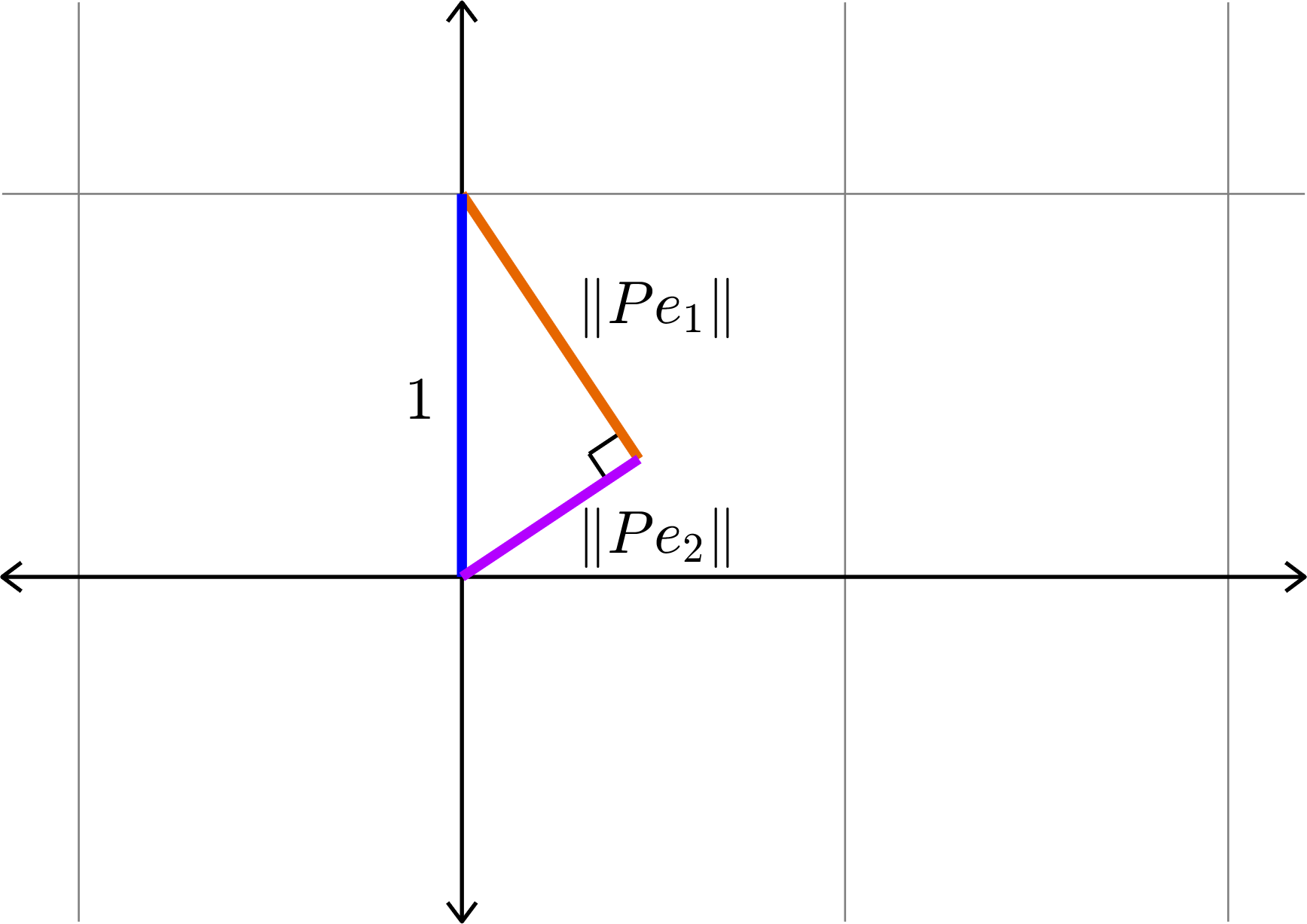
\[\|Pe_{1}\|^{2} + \|Pe_{2}\|^{2} = 1\]
The Pythagorean Theorem
Theorem. If \(P\) is an orthogonal projection onto a \(1\)-dimensional subspace \(V\), and \(\{e_{1},e_{2},\ldots,e_{n}\}\) is an orthonormal basis, then
\[\sum_{i=1}^{n}\|Pe_{i}\|^{2} = 1.\]
Proof.
- Let \(v\in V\) be a unit vector.
- \(Px = \langle x,v\rangle v,\)
- \(\|Pe_{i}\|^{2} = |\langle e_{i},v\rangle|^{2}\)
- \(\displaystyle{\sum_{i=1}^{n}\|Pe_{i}\|^{2} = \sum_{i=1}^{n}|\langle e_{i},v\rangle|^{2} = \|v\|^{2} = 1}.\)
\(\Box\)
The Pythagorean Theorem and Diagonals
If \(P\) is an orthogonal projection onto a subspace \(V\), and \((e_{i})_{i=1}^{n}\) is an orthonormal basis, then
\[\|Pe_{i}\|^{2} = \langle Pe_{i},Pe_{i}\rangle = \langle P^{\ast}Pe_{i},e_{i}\rangle = \langle P^{2}e_{i},e_{i}\rangle = \langle Pe_{i},e_{i}\rangle\]
\[ = \left[\begin{array}{cccc} \|Pe_{1}\|^{2} & \ast & \cdots & \ast\\ \overline{\ast} & \|Pe_{2}\|^{2} & & \vdots\\ \vdots & & \ddots & \vdots\\ \overline{\ast} & \cdots & \cdots & \|Pe_{n}\|^{2}\end{array}\right] \]
\[P= \left[\begin{array}{cccc} \langle Pe_{1},e_{1}\rangle & \langle Pe_{2},e_{1}\rangle & \cdots & \langle Pe_{n},e_{1}\rangle \\ \langle Pe_{1},e_{2}\rangle & \langle Pe_{2},e_{2}\rangle & & \vdots\\ \vdots & & \ddots & \vdots\\ \langle Pe_{1},e_{n}\rangle & \cdots & \cdots & \langle Pe_{n},e_{n}\rangle \end{array}\right]\]
The Pythagorean Theorem
Theorem. If \(P\) is an orthogonal projection onto a \(1\)-dimensional subspace \(V\), and \(\{e_{1},e_{2},\ldots,e_{n}\}\) is an orthonormal basis, then
\[\sum_{i=1}^{n}\|Pe_{i}\|^{2} = 1.\]
Proof. \[\sum_{i=1}^{n}\|Pe_{i}\|^{2} = \text{tr}(P) = \dim V = 1.\]
\(\Box\)
The Pythagorean Theorem
Theorem. If \(P\) is an orthogonal projection onto a \(k\)-dimensional subspace \(V\), and \(\{e_{1},e_{2},\ldots,e_{n}\}\) is an orthonormal basis, then
\[\sum_{i=1}^{n}\|Pe_{i}\|^{2} = k.\]
Proof. \[\sum_{i=1}^{n}\|Pe_{i}\|^{2} = \text{tr}(P) = \dim V = k.\]
\(\Box\)
Kadison's Pythagorean Theorem (finite dimensional)
Theorem. If \(P\) is an orthogonal projection onto a \(k\)-dimensional subspace \(V\), and \(\{e_{1},e_{2},\ldots,e_{n}\}\) is an orthonormal basis, then
\[\sum_{i=1}^{n}\|Pe_{i}\|^{2} = k.\]
Proof. \[\sum_{i=1}^{n}\|Pe_{i}\|^{2} = \text{tr}(P) = \dim V = k.\]
\(\Box\)
Corollary. If \(P\) is an orthogonal projection onto a \(k\)-dimensional subspace, and \((d_{i})_{i=1}^{n}\) is the sequence on the diagonal of \(P\), then
\(d_{i}\in[0,1]\) for each \(i\), and
\[\sum_{i=1}^{n}d_{i} \in\Z\]
The Carpenter's Theorem
Theorem. If \(\Delta\) is a triangle with side lengths \(c\geq b\geq a\), such that
\(a^{2}+b^{2}=c^{2},\) then \(\Delta\) is a right triangle.
\(a\)
\(b\)
\(c\)
Proof. Law of cosines
\[c^2=a^2+b^2-2ab\cos(\theta).\]
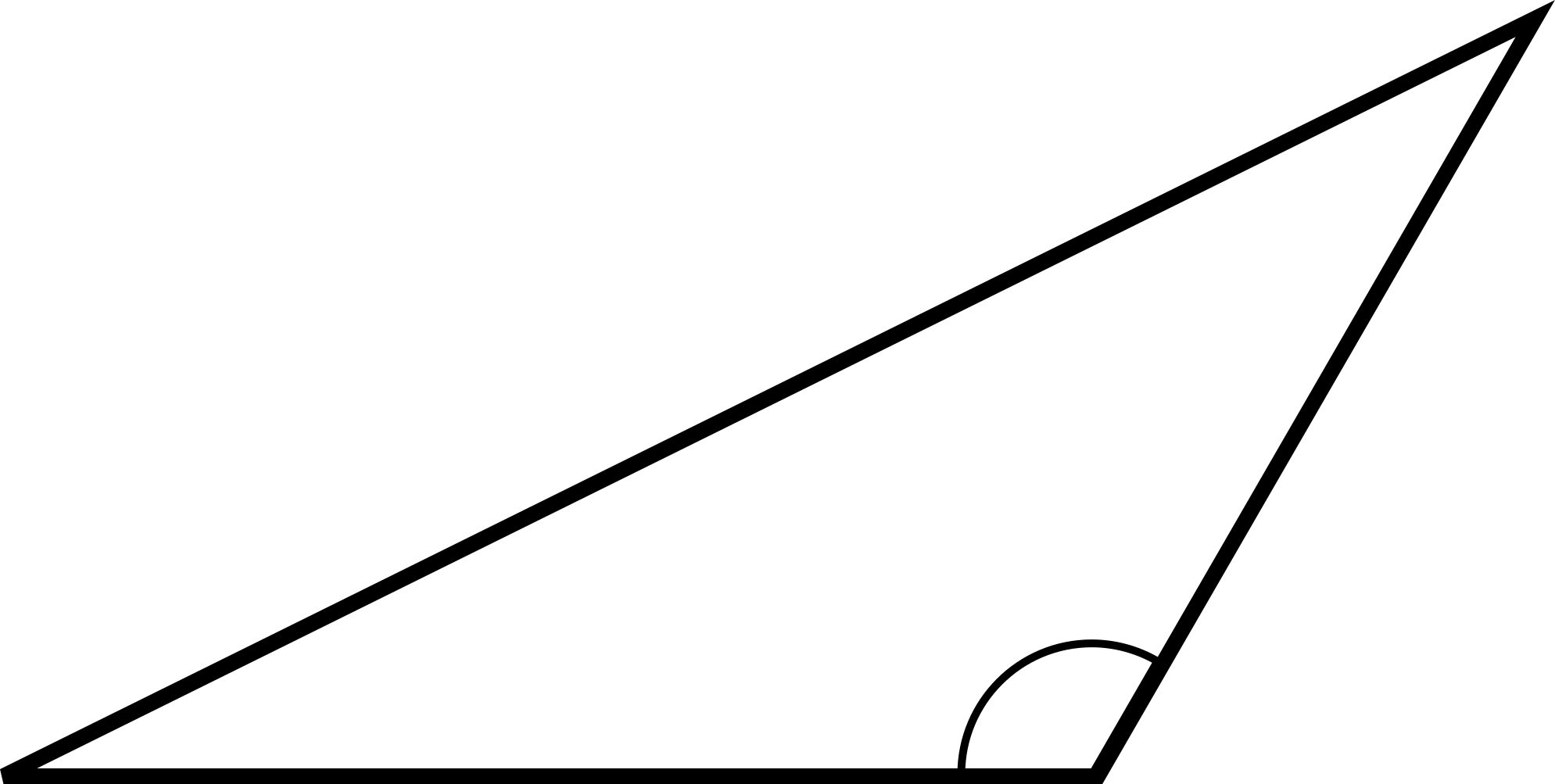
\(\theta\)
Theorem. If \(v\) and \(w\) are vectors in a real Hilbert space such that
\(\|v\|^2 + \|w\|^2 = \|v+w\|^2,\) then \(\langle v,w\rangle = 0.\)
The Carpenter's Theorem
Proof.
\[\|v+w\|^2 = \langle v+w,v+w\rangle = \|v\|^2+2\langle v,w\rangle + \|w\|^{2}\]
\[\|v+w\|^2=\|v\|^2+\|w\|^2 \quad \Rightarrow\quad 2\langle v,w\rangle = 0. \quad \Box\]
Theorem. If \(d_{1},d_{2}\) are two numbers in \([0,1]\) such that \(d_{1}+d_{2} = 1,\) then there is a projection \(P\) such that \(d_{1} = \|Pe_{1}\|^2\) and \(d_{2} = \|Pe_{2}\|^2\), that is,
\[P = \begin{bmatrix} d_{1} & \alpha\\ \overline{\alpha} & d_{2}\end{bmatrix}.\]
Kadison's Carpenter's Theorem (2d)

Proof.
- By the intermediate value theorem there is a projection \(P\) such that \(\|Pe_{1}\|^{2}=d_{1}.\)
- By the Pythagorean theorem \(\|Pe_{1}\|^2+\|Pe_{2}\|^2=1.\)
- Therefore, \[\|Pe_{2}\|^2=d_{2}.\]
Theorem. If \((d_{i})_{i=1}^{n}\) is a sequence of numbers in \([0,1]\) such that \[\sum_{i=1}^{n}d_{i}\in\N\cup\{0\},\] then there is an \(n\times n\) projection \(P\) such that \[\|Pe_{i}\|^{2} = d_{i} \quad\text{for}\quad i=1,\ldots,n.\]
Kadison's Carpenter's Theorem
\[\langle Pe_{i},e_{i}\rangle = \]
Note that this means that the sequence on the diagonal of the matrix \(P\) is \((d_{i})_{i=1}^{n}\).
Example. Consider the sequence
\[\left(\frac{5}{7},\frac{5}{7},\frac{3}{7},\frac{1}{7}\right).\]
\[\left[\begin{array}{rrrr}\frac{5}{7} & -\frac{\sqrt{15}}{21} & -\frac{\sqrt{30}}{21} & \frac{\sqrt{5}}{7}\\[1ex] -\frac{\sqrt{15}}{21} & \frac{5}{7} & -\frac{2\sqrt{2}}{7} & -\frac{\sqrt{3}}{21}\\[1ex] -\frac{\sqrt{30}}{21} & -\frac{2\sqrt{2}}{7} & \frac{3}{7} & -\frac{\sqrt{6}}{21}\\[1ex] \frac{\sqrt{5}}{7} & -\frac{\sqrt{3}}{21} & -\frac{\sqrt{6}}{21} & \frac{1}{7}\end{array}\right]\]
Challenge: Construct a \(4\times 4\) projection with this diagonal.
Theorem. Assume \((d_{i})_{i=1}^{n}\) is a sequence of numbers in \([0,1].\) There is an \(n\times n\) projection \(P\) with diagonal \((d_{i})_{i=1}^{n}\) if and only if
\[\sum_{i=1}^{n}d_{i} \in\N\cup\{0\}.\]
Characterization of Diagonals of Projections
in Finite Dimensions
Diagonality
Definition. Given an operator \(E\) on a Hilbert space, a sequence \((d_{i})_{i\in I}\) is a diagonal of \(E\) if there is an orthonormal basis \((e_{i})_{i\in I}\) such that
\[d_{i} = \langle Ee_{i},e_{i}\rangle \quad\text{for all }i\in I.\]
The problem: Given an operator \(E\), characterize the set of diagonals of \(E\), that is, the set
\[\big\{(\langle Ee_{i},e_{i}\rangle )_{i\in I} : (e_{i})_{i\in I}\text{ is an orthonormal basis}\big\}\]
In particular, we want a characterization in terms of linear inequalities between the diagonal sequences and the spectral information of \(E\).
Diagonals of projections in finite dimensions
Diagonals of projections in infinite dimensions
Diagonals of self-adjoint matrices in finite dimensions
Compact positive
Normal
self-adjoint finite spectrum
\(\mathrm{II}_{1}\) factors
W/ prescribed singular values
Normal
Two paths forward
?
\(\infty\) dimensional path
Finite dimensional path
Projections in infinite dimensions
Examples. Let \((e_{i})_{i=1}^{\infty}\) be an orthonormal basis.
Set \(\displaystyle{v = \sum_{i=1}^{\infty}\sqrt{\frac{1}{2^{i}}}e_{i}},\) then
\[I-P = \begin{bmatrix} \frac{1}{2} & -\frac{1}{2^{3/2}} & -\frac{1}{2^{2}} & \cdots \\[1ex] -\frac{1}{2^{3/2}} & \frac{3}{4} & -\frac{1}{2^{5/2}} & \cdots\\[1ex] -\frac{1}{2^{2}} & -\frac{1}{2^{5/2}} & \frac{7}{8} & \cdots\\ \vdots & \vdots & \vdots & \ddots\end{bmatrix}\]
\[P = \langle \cdot,v\rangle v = \begin{bmatrix} \frac{1}{2} & \frac{1}{2^{3/2}} & \frac{1}{2^{2}} & \cdots \\[1ex] \frac{1}{2^{3/2}} & \frac{1}{4} & \frac{1}{2^{5/2}} & \cdots\\[1ex] \frac{1}{2^{2}} & \frac{1}{2^{5/2}} & \frac{1}{8} & \cdots\\[1ex] \vdots & \vdots & \vdots & \ddots\end{bmatrix}\]
Corank 1 projection
Diagonal: \(\displaystyle{\left(\frac{1}{2},\frac{3}{4},\frac{7}{8},\ldots\right)}\)
Rank 1 projection
Diagonal: \(\displaystyle{\left(\frac{1}{2},\frac{1}{4},\frac{1}{8},\ldots\right)}\)
Projections in infinite dimensions
Examples.
\[\frac{1}{2}J_{2} = \begin{bmatrix} \frac{1}{2} & \frac{1}{2}\\[1ex] \frac{1}{2} & \frac{1}{2}\end{bmatrix}\]
\[Q = \bigoplus_{i=1}^{\infty}\frac{1}{2}J_{2} = \begin{bmatrix} \frac{1}{2}J_{2} & \mathbf{0} & \mathbf{0} & \cdots\\ \mathbf{0} & \frac{1}{2}J_{2} & \mathbf{0} & \cdots\\ \mathbf{0} & \mathbf{0} & \frac{1}{2}J_{2} & \\ \vdots & \vdots & & \ddots\end{bmatrix}\]
\(\infty\)-rank and \(\infty\)-corank
Diagonal: \(\displaystyle{\left(\frac{1}{2},\frac{1}{2},\frac{1}{2},\ldots\right)}\)
\(\infty\)-rank and \(\infty\)-corank
Diagonal: \(\displaystyle{\left(\ldots,\frac{1}{8},\frac{1}{4},\frac{1}{2},\frac{1}{2},\frac{3}{4},\frac{7}{8},\ldots\right)}\)
\[P\oplus (I-P)\]
Theorem. Assume \((d_{i})_{i=1}^{n}\) is a sequence of numbers in \([0,1].\) There is an \(n\times n\) projection \(P\) with diagonal \((d_{i})_{i=1}^{n}\) if and only if
\[\sum_{i=1}^{n}d_{i} \in\N\cup\{0\}.\]
Diagonals of Projections Redux
\[\sum_{i=1}^{k}d_{i} - \sum_{i=k+1}^{n}(1-d_{i})\in\Z\]
\[\Updownarrow\]
Theorem. Assume \((d_{i})_{i=1}^{n}\) is a sequence of numbers in \([0,1].\) There is an \(n\times n\) projection \(P\) with diagonal \((d_{i})_{i=1}^{n}\) if and only if
\[\sum_{i=1}^{k}d_{i} - \sum_{i=k+1}^{n}(1-d_{i})\in\Z.\]
Diagonals of Projections Redux
Theorem (Kadison '02). Assume \((d_{i})_{i=1}^{\infty}\) is a sequence of numbers in \([0,1],\) and set
\[a=\sum_{d_{i}<\frac{1}{2}}d_{i}\quad\text{and}\quad b=\sum_{d_{i}\geq \frac{1}{2}}(1-d_{i})\]
There is a projection \(P\) with diagonal \((d_{i})_{i=1}^{\infty}\) if and only if one of the following holds:
- \(a=\infty\)
- \(b=\infty\)
- \(a,b<\infty\) and \(a-b\in\Z\)
Kadison's Theorem
Examples.
- There is a projection with every number in \(\mathbb{Q}\cap[0,1]\) on the diagonal.
- There is a projection with diagonal \((\frac{\pi}{4},\frac{\pi}{4},\frac{\pi}{4},\ldots)\).
- There is no projection with diagonal \[\left(\ldots,\frac{1}{25},\frac{1}{16},\frac{1}{9},\frac{1}{4},\frac{1}{2},\frac{3}{4},\frac{7}{8},\frac{15}{16},\ldots\right)\]
Diagonals of projections in finite dimensions
Diagonals of projections in infinite dimensions
Diagonals of self-adjoint matrices in finite dimensions
Compact positive
Normal
self-adjoint finite spectrum
\(\mathrm{II}_{1}\) factors
W/ prescribed singular values
Normal
Two paths forward
?
The Schur-Horn Theorem
Theorem (Schur '23, Horn '54). Let \((d_{i})_{i=1}^{n}\) and \((\lambda_{i})_{i=1}^{n}\) be nonincreasing sequences. There is a self-adjoint matrix \(E\) with diagonal \((d_{i})_{i=1}^{n}\) and eigenvalues \((\lambda_{i})_{i=1}^{n}\) if and only if
\[\sum_{i=1}^{k}d_{i}\leq \sum_{i=1}^{k}\lambda_{i}\quad\text{for}\quad k=1,2,\ldots,n-1\]
and
\[\sum_{i=1}^{n}d_{i} = \sum_{i=1}^{n}\lambda_{i}.\]
(1)
(2)
If (1) and (2) hold, then we say that \((\lambda_{i})_{i=1}^{n}\) majorizes \((d_{i})_{i=1}^{n}\), and we write \((\lambda_{i})_{i=1}^{n}\succeq (d_{i})_{i=1}^{n}\)
\((\lambda_{i})_{i=1}^{n}\succeq (d_{i})_{i=1}^{n}\) is equivalent to saying that \((d_{i})_{i=1}^{n}\) is in the convex hull of the permutations of \((\lambda_{i})_{i=1}^{n}\).
Diagonals of projections in finite dimensions
Diagonals of projections in infinite dimensions
Diagonals of self-adjoint matrices in finite dimensions
Compact positive
Normal
self-adjoint finite spectrum
\(\mathrm{II}_{1}\) factors
W/ prescribed singular values
Normal
Two paths forward
?
Theorem (Arveson, Kadison '06, Kaftal, Weiss '10). Let \((\lambda_{i})_{i=1}^{\infty}\) be a positive nonincreasing sequence, and let \((d_{i})_{i=1}^{\infty}\) be a nonnegative nonincreasing sequence. There exists a positive compact operator with diagonal \((d_{i})_{i=1}^{\infty}\) and whose positive eigenvalues are \((\lambda_{i})_{i=1}^{\infty}\) if and only if
\[\sum_{i=1}^{k}d_{i}\leq \sum_{i=1}^{k}\lambda_{i}\quad\text{for all}\quad k\in\N\]
and
\[\sum_{i=1}^{\infty}d_{i} = \sum_{i=1}^{\infty}\lambda_{i}.\]
Open question: What are the diagonals of positive compact operators with positive eigenvalues
\[\left(1,\frac{1}{2},\frac{1}{3},\ldots\right)\] and a \(1\)-dimensional kernel.
Diagonals of projections in finite dimensions
Diagonals of projections in infinite dimensions
Diagonals of self-adjoint matrices in finite dimensions
Compact positive
Normal
self-adjoint finite spectrum
W/ prescribed singular values
Normal
Two paths forward
?
\(\mathrm{II}_{1}\) factors
?
Three Point Spectrum
Theorem (JJ '13). Let \(0<\alpha<1\) and let \((d_{i})_{i=1}^{\infty}\) be a sequence in \([0,1]\). Define
\[c=\sum_{d_{i}<\alpha}d_{i}\quad\text{and}\quad d=\sum_{d_{i}\geq \alpha}(1-d_{i}).\]
There is a self-adjoint operator \(E\) with diagonal \((d_{i})_{i=1}^{\infty}\) and spectrum \(\{0,\alpha,1\}\) if and only if one of the following holds:
- \(c=\infty\)
- \(d=\infty\)
- \(c,d<\infty\) and there exist \(N\in\N\) and \(k\in\Z\) such that \[c-d=N\alpha+k\quad\text{and}\quad c\geq (N+k)\alpha.\]
Notes:
- There is a longer version where the multiplicities of the eigenvalues are considered.
- Together with Marcin Bownik we extended this to all self-adjoint operators with a finite spectrum.
\[E=\left(\begin{array}{ccccccc} 1/2 & \overline{\ast} & \overline{\ast} & \overline{\ast} & \overline{\ast} & \cdots\\ \ast & 1/4 & \overline{\ast} & \overline{\ast} & \overline{\ast} & \cdots\\ \ast & \ast & 3/4 & \overline{\ast} & \overline{\ast} & \cdots\\ \ast & \ast & \ast & 1/8 & \overline{\ast} & \cdots\\ \ast & \ast & \ast & \ast & 7/8 & \\ \vdots & \vdots & \vdots & \vdots & & \ddots\\ \end{array}\right)\]
An application
Consider the self-adjoint operator
If the eigenvalues of \(E\) are \(\{0,\alpha,1\}\) with \(0<\alpha<1\), then what are the possible values of \(\alpha\)?
\[ \frac{1}{16},\frac{1}{14},\frac{1}{12},\frac{1}{10},\frac{1}{8},\frac{1}{6},\frac{1}{4},\frac{1}{2},\frac{3}{4},\frac{5}{6},\frac{7}{8},\frac{9}{10},\frac{11}{12},\frac{13}{14},\frac{15}{16}\]
Diagonals of projections in finite dimensions
Diagonals of projections in infinite dimensions
Diagonals of self-adjoint matrices in finite dimensions
Compact positive
Normal
self-adjoint finite spectrum
W/ prescribed singular values
Normal
What's left?
?
\(\mathrm{II}_{1}\) factors
Infinite dimensions:
- Compact positive operators: What about finite dimensional kernels?
- Normal operators: Arveson proved a generalization of Kadison's Pythagorean theorem that applies to very special normal operators.
- \(\mathrm{II}_{1}\) factors: Ravichandran announced a solution in 2012, but it has not appeared in print.
- and much more...
What's left?
Finite dimensions:
- Normal operators: Diagonals of \(3\times 3\) normal matrices was worked out by Williams in 1971, but the \(4\times 4\) case is still open.
- Matrices with prescribed singular values: Thompson 1977
Georgetown Colloquium
By John Jasper
Georgetown Colloquium
- 509



