Toward a Taxonomy of Real Equiangular Tight Frames
John Jasper
South Dakota State University

JMM 2022

Darwin's Orchid


Charles Darwin
(1809-1882)
Predicted 1862
Discovered 1903
Angraecum sesquipedale
Vectors that are as spread out as possible
Theorem (the Welch bound). Given a collection of unit vectors \(\Phi=(\varphi_{i})_{i=1}^{N}\) in \(\mathbb{C}^d\), the coherence satisfies
\[\mu(\Phi):=\max_{i\neq j}|\langle \varphi_{i},\varphi_{j}\rangle|\geq \sqrt{\frac{N-d}{d(N-1)}}.\]
Equality holds if and only if the following two conditions hold:
- Tight: There is a constant \(A>0\) such that \[\sum_{i=1}^{N}|\langle v,\varphi_{i}\rangle|^{2} = A\|v\|^{2} \quad\text{for all } v.\]
- Equiangular: There is a constant \(\alpha\) such that \[|\langle\varphi_{i},\varphi_{j}\rangle| = \alpha\quad\text{for all }i\neq j.\]
A collection of equal norm vectors which is both equiangular and tight is known as an equiangular tight frame (ETF). These are also known as Welch bound equality codes.
Examples of equiangular tight frames
Example 2. Consider the (multiple of a) unitary matrix
Example 1. Consider the (multiple of a) unitary matrix
\[\left[\begin{array}{rrrr}1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1\end{array}\right]\]
\[\left[\begin{array}{rrrr} 1 & 1 & 1 & 1\\ 1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1\end{array}\right]\]
\[\left[\begin{array}{rrrr} 1 & 1 & 1\\ \sqrt{2} & -\sqrt{\frac{1}{2}} & -\sqrt{\frac{1}{2}}\\ 0 & \sqrt{\frac{3}{2}} & -\sqrt{\frac{3}{2}}\end{array}\right]\]
\[\left[\begin{array}{rrrr}\sqrt{2} & -\sqrt{\frac{1}{2}} & -\sqrt{\frac{1}{2}}\\ 0 & \sqrt{\frac{3}{2}} & -\sqrt{\frac{3}{2}}\end{array}\right]\]
Examples of equiangular tight frames
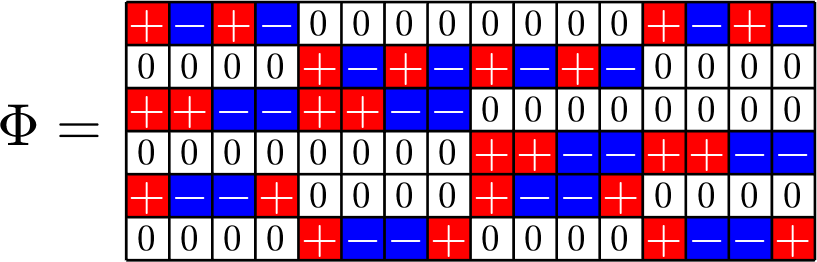
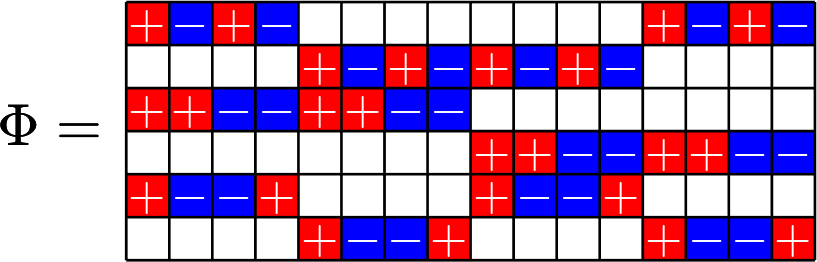
Example 3.

Steiner Systems
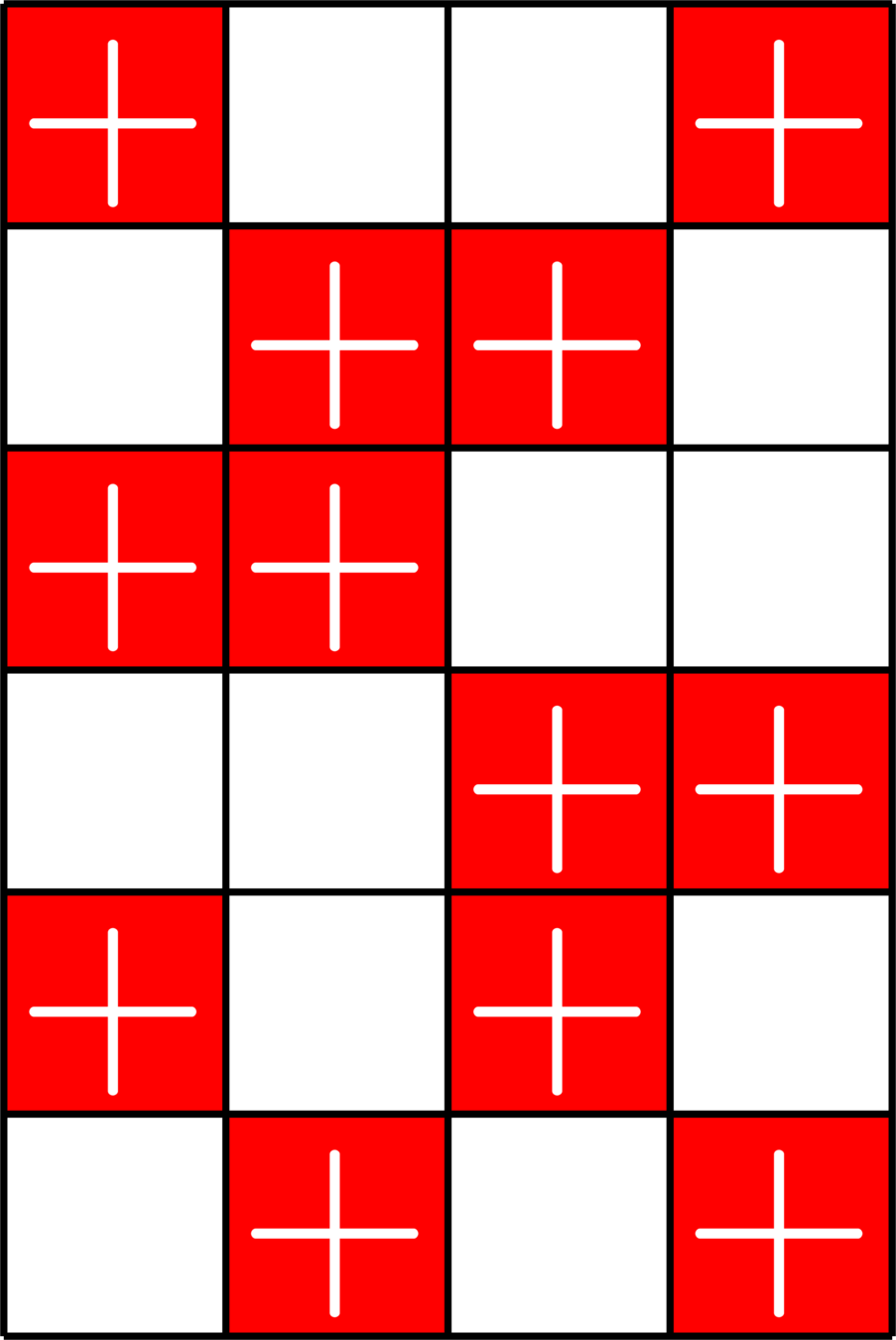
Definition. A \((2,k,v)\)-Steiner system \(\{0,1\}\)-matrix \(X\) with the following properties:
- Each row of \(X\) has exactly \(k\) ones.
- Each column of \(X\) has exactly \(r=\frac{v-1}{k-1}\) ones.
- The dot product of any distinct pair of columns is one.
Example. The matrix
\(X = \)
is a \((2,2,4)\)-Steiner system.

The Star Product

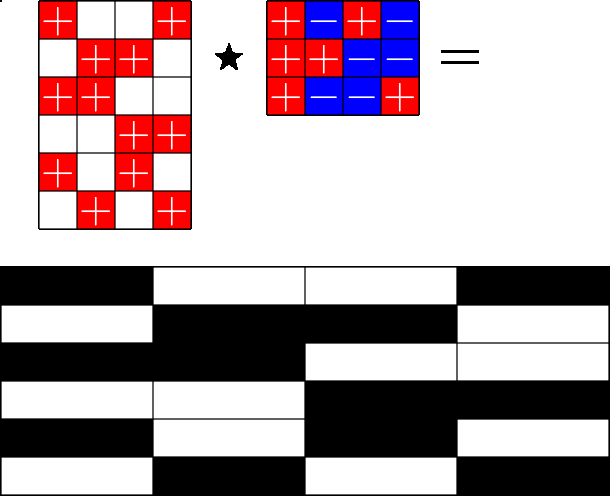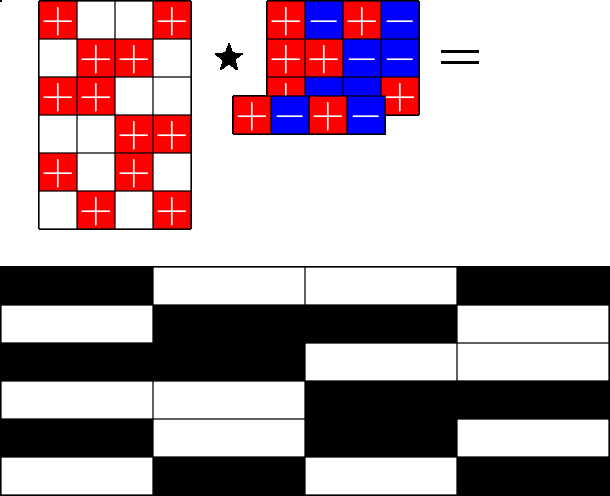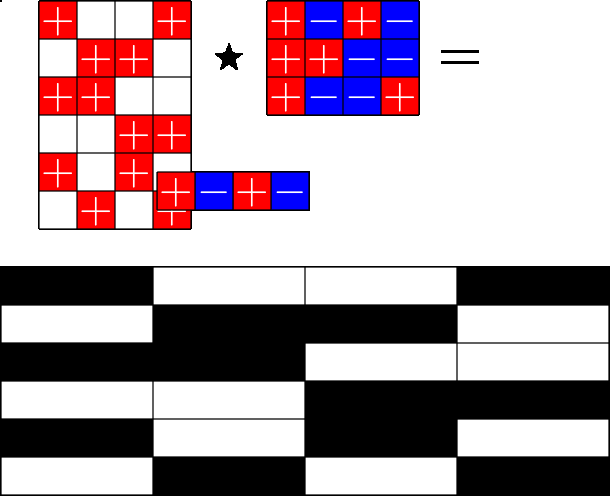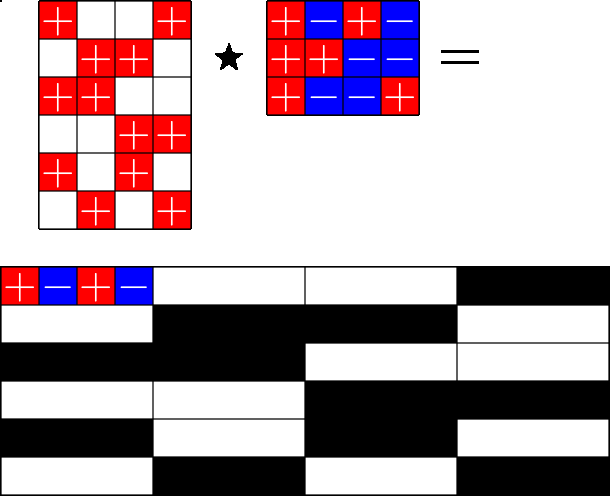
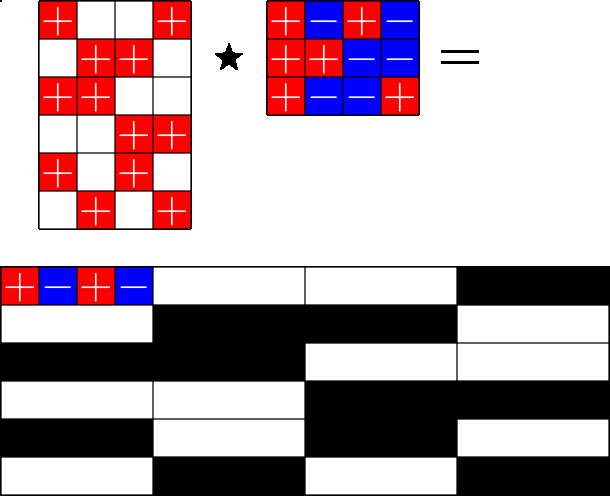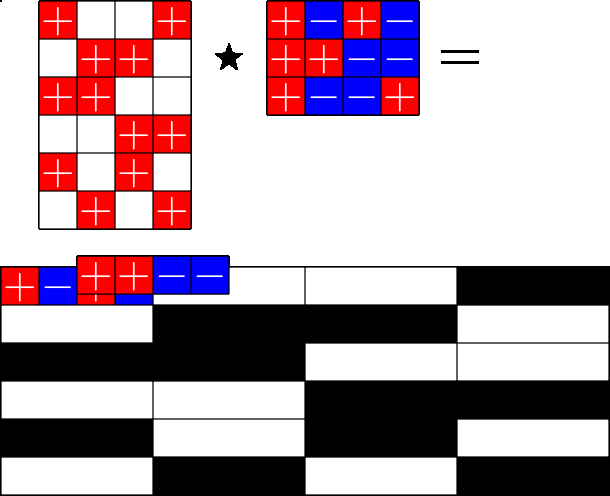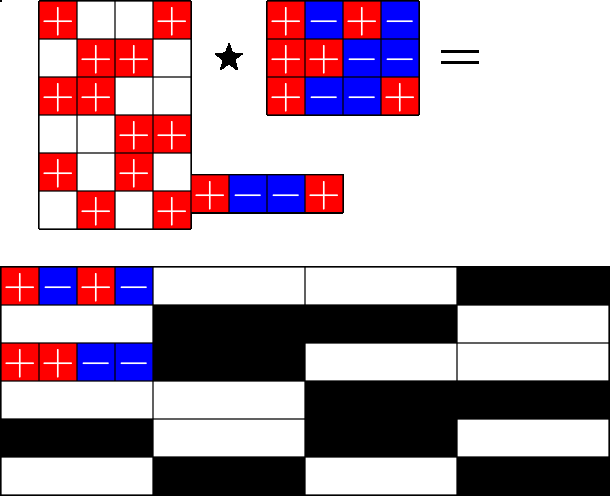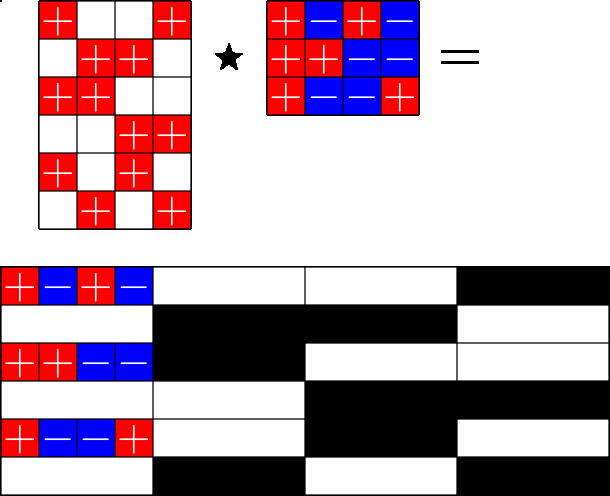
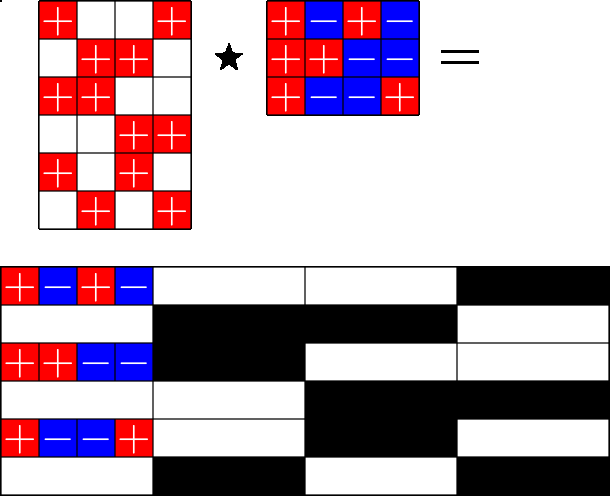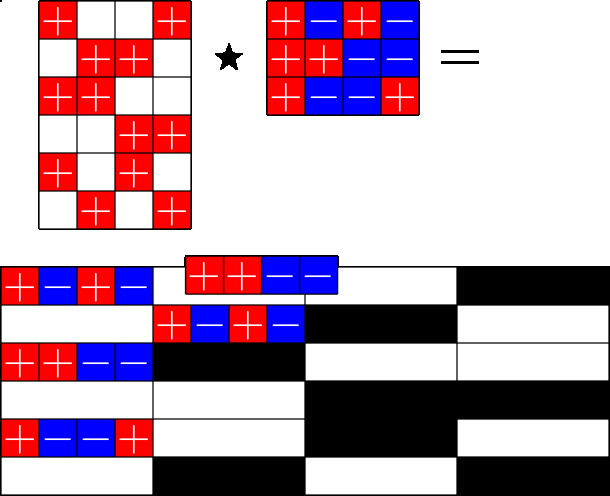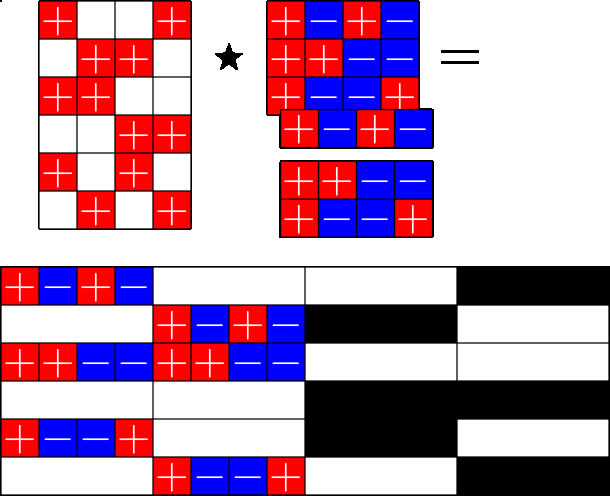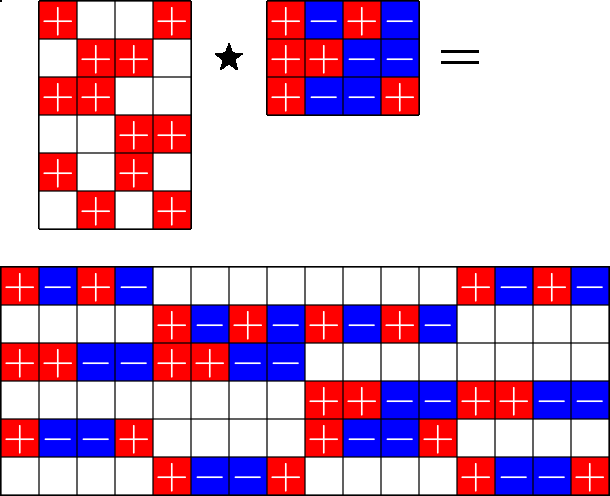
Our first "species" of ETF: Steiner ETFs
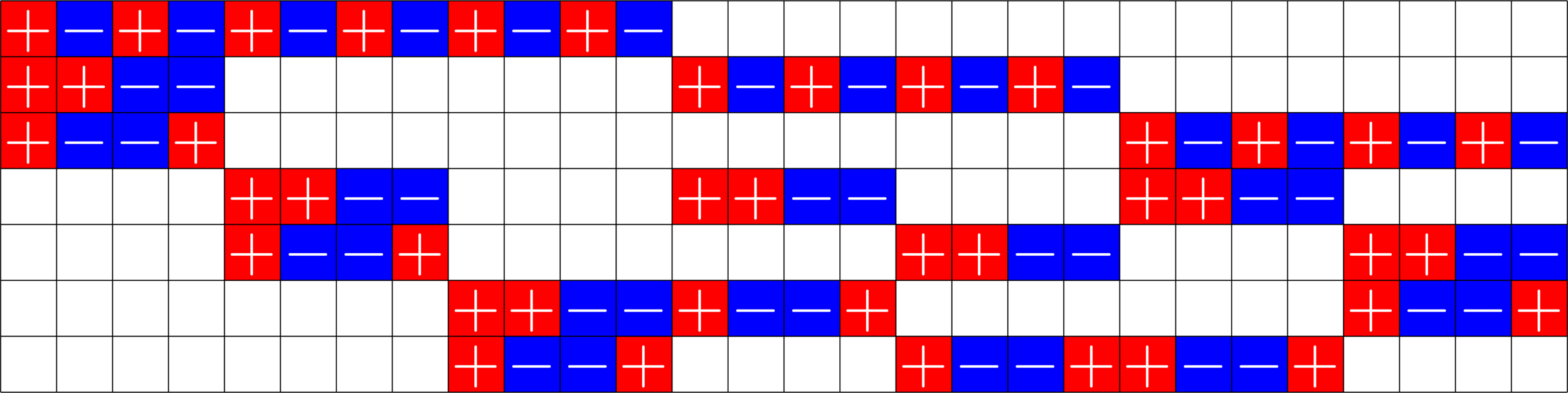


\(=\)
Take a Steiner system with \(r\) ones per column
and an \(r\times (r+1)\) ETF with unimodular entries
The Star product is a "Steiner" ETF


What species is this?
*ETF table by Dustin Mixon and Matt Fickus
, Spence difference set
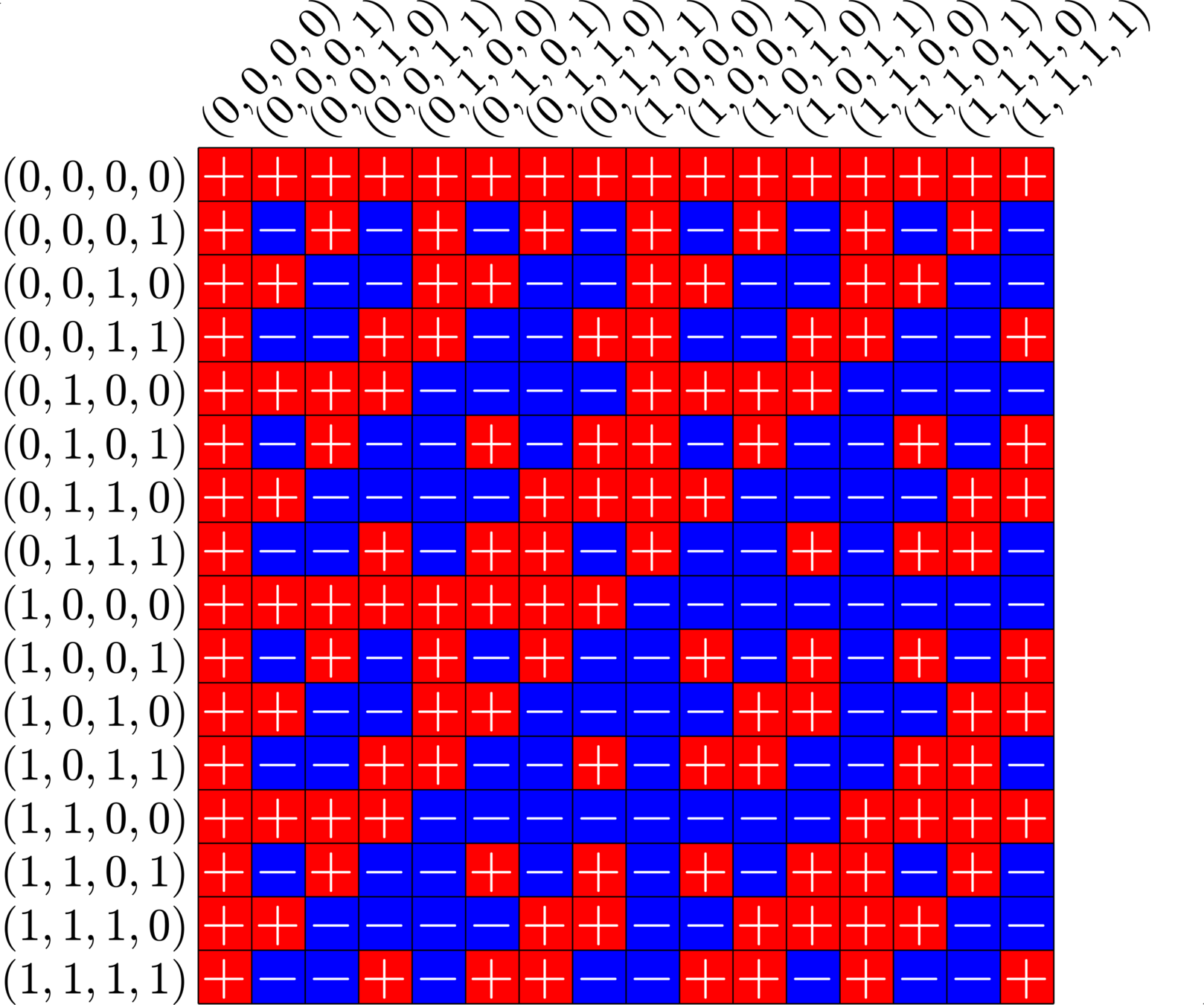
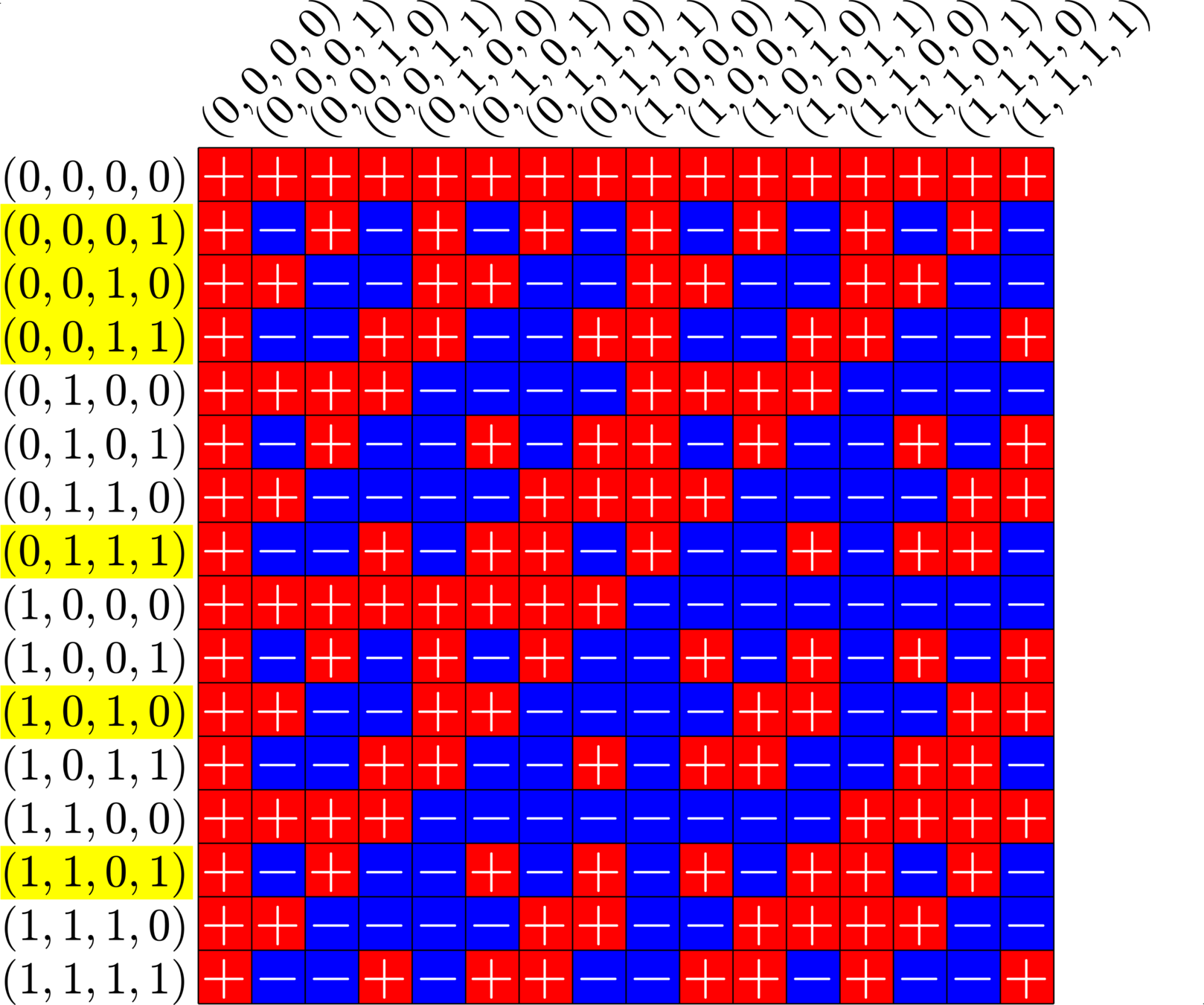
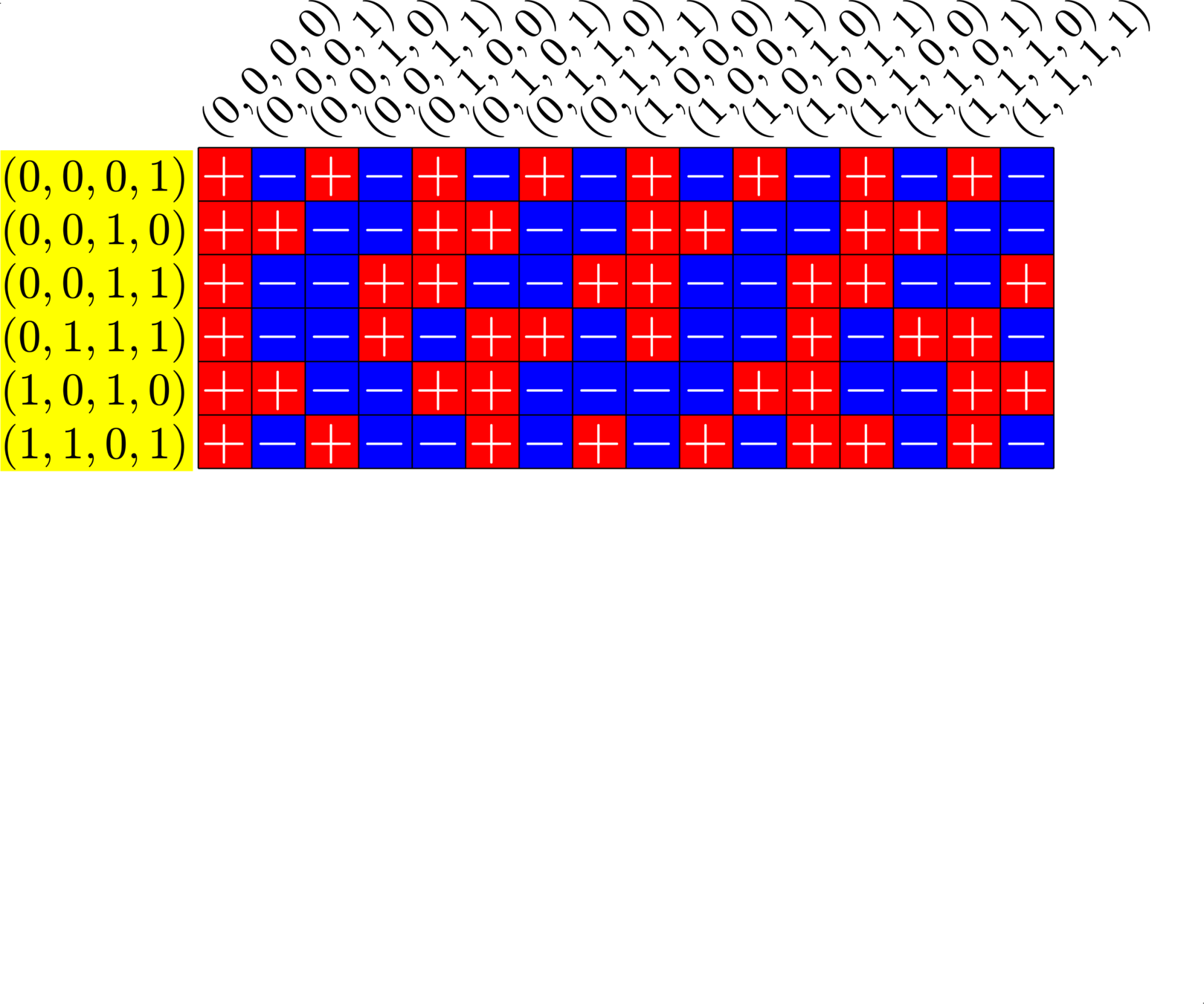
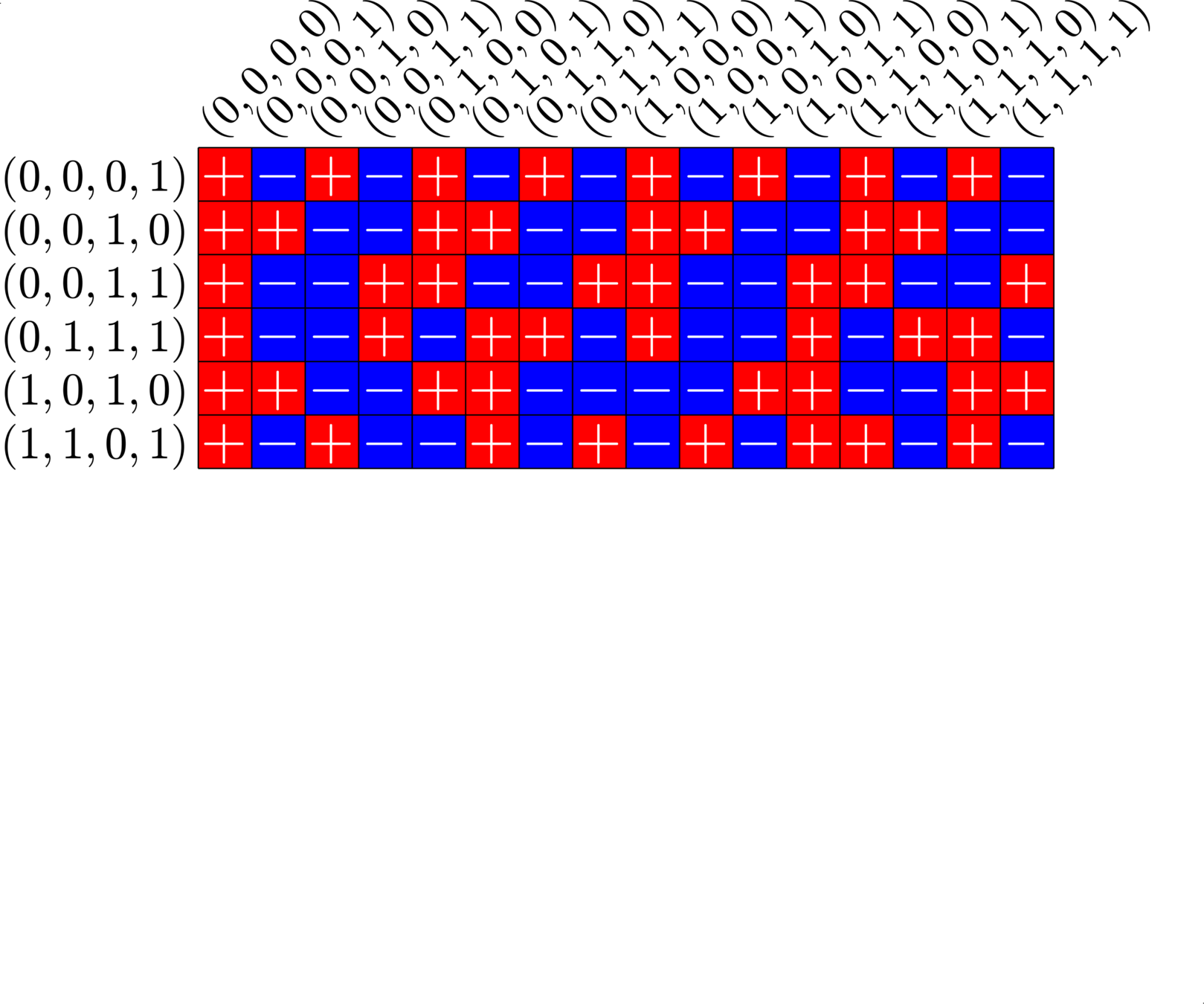
\[\begin{array}{c|cccccc} & (0,0,0,1) & (1,1,0,1) & (0,0,1,0) & (1,0,1,0) & (0,0,1,1) & (0,1,1,1)\\ \hline (0,0,0,1) & (0,0,0,0) & (1,1,0,0) & (0,0,1,1) & (1,0,1,1) & (0,0,1,0) & (0,1,1,0)\\ (1,1,0,1) & (1,1,0,0) & (0,0,0,0) & (1,1,1,1) & (0,1,1,1) & (1,1,1,0) & (1,0,1,0)\\ (0,0,1,0) & (0,0,1,1) & (1,1,1,1) & (0,0,0,0) & (1,0,0,0) & (0,0,0,1) & (0,1,0,1)\\ (1,0,1,0) & (1,0,1,1) & (0,1,1,1) & (1,0,0,0) & (0,0,0,0) & (1,0,0,1) &(1,1,0,1)\\ (0,0,1,1) & (0,0,1,0) & (1,1,1,0) & (0,0,0,1) & (1,0,0,1) & (0,0,0,0) & (0,1,0,0)\\ (0,1,1,1) & (0,1,1,0) & (1,0,1,0) & (0,1,0,1) & (1,1,0,1) & (0,1,0,0) & (0,0,0,0) \end{array}\]
\[D=\{(0,0,0,1),(0,0,1,0),(0,0,1,1),(0,1,1,1),(1,0,1,0),(1,1,0,1)\}\]
is a (McFarland) difference set in \(G=\Z_{2}\times\Z_{2}\times\Z_{2}\times\Z_{2}\)
A McFarland difference set
Each nonzero element appears exactly twice in the difference table:
A McFarland difference set
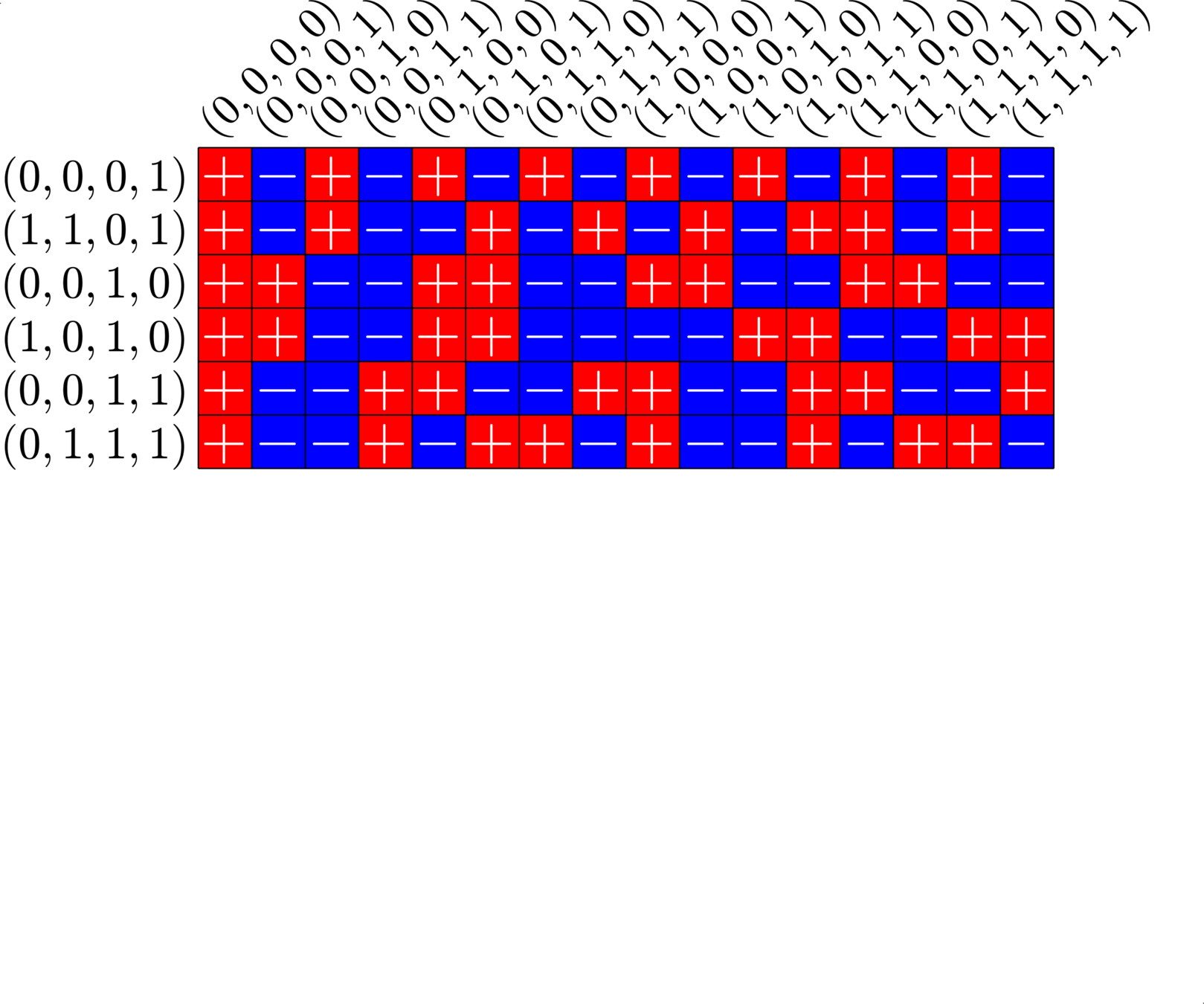
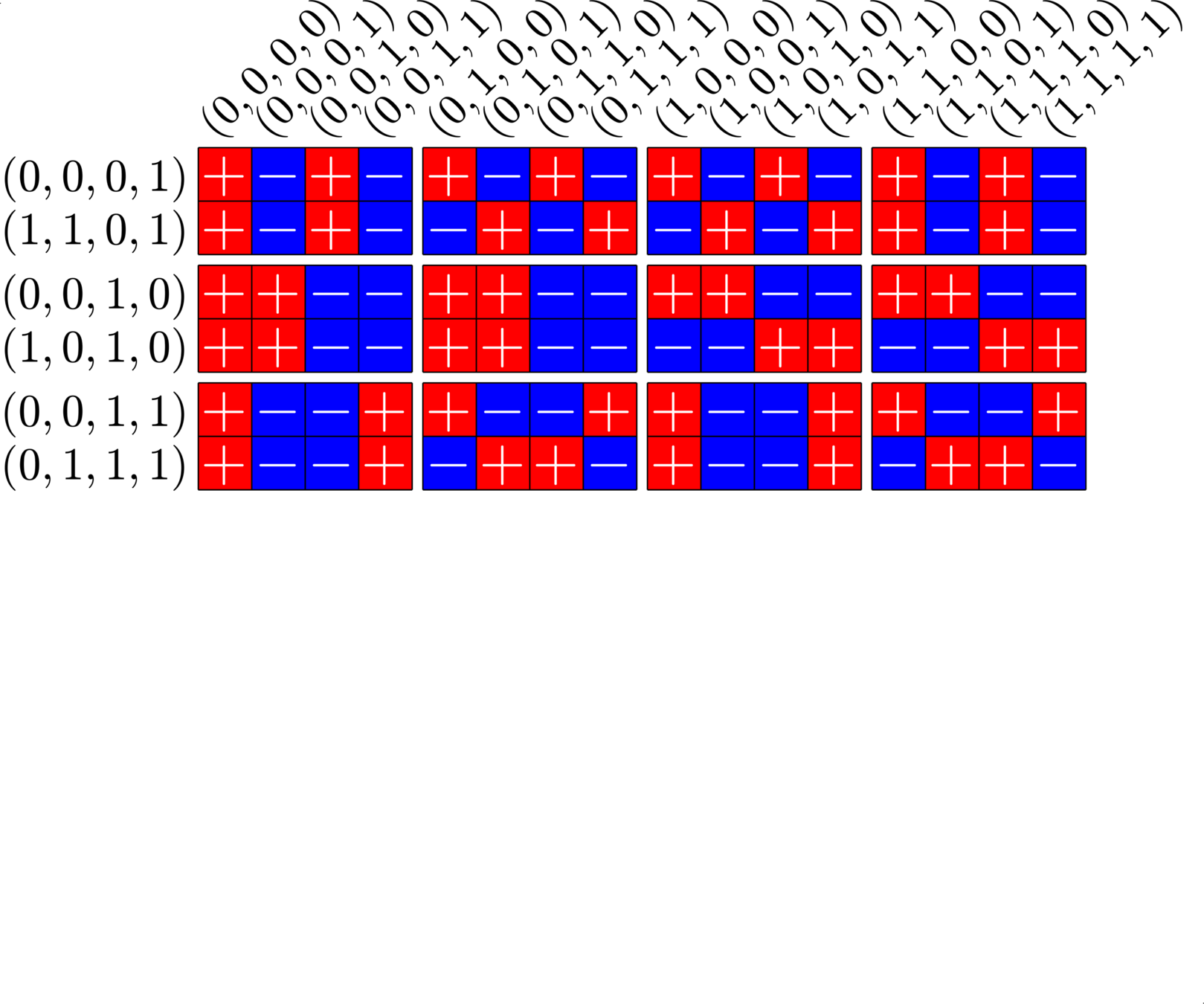


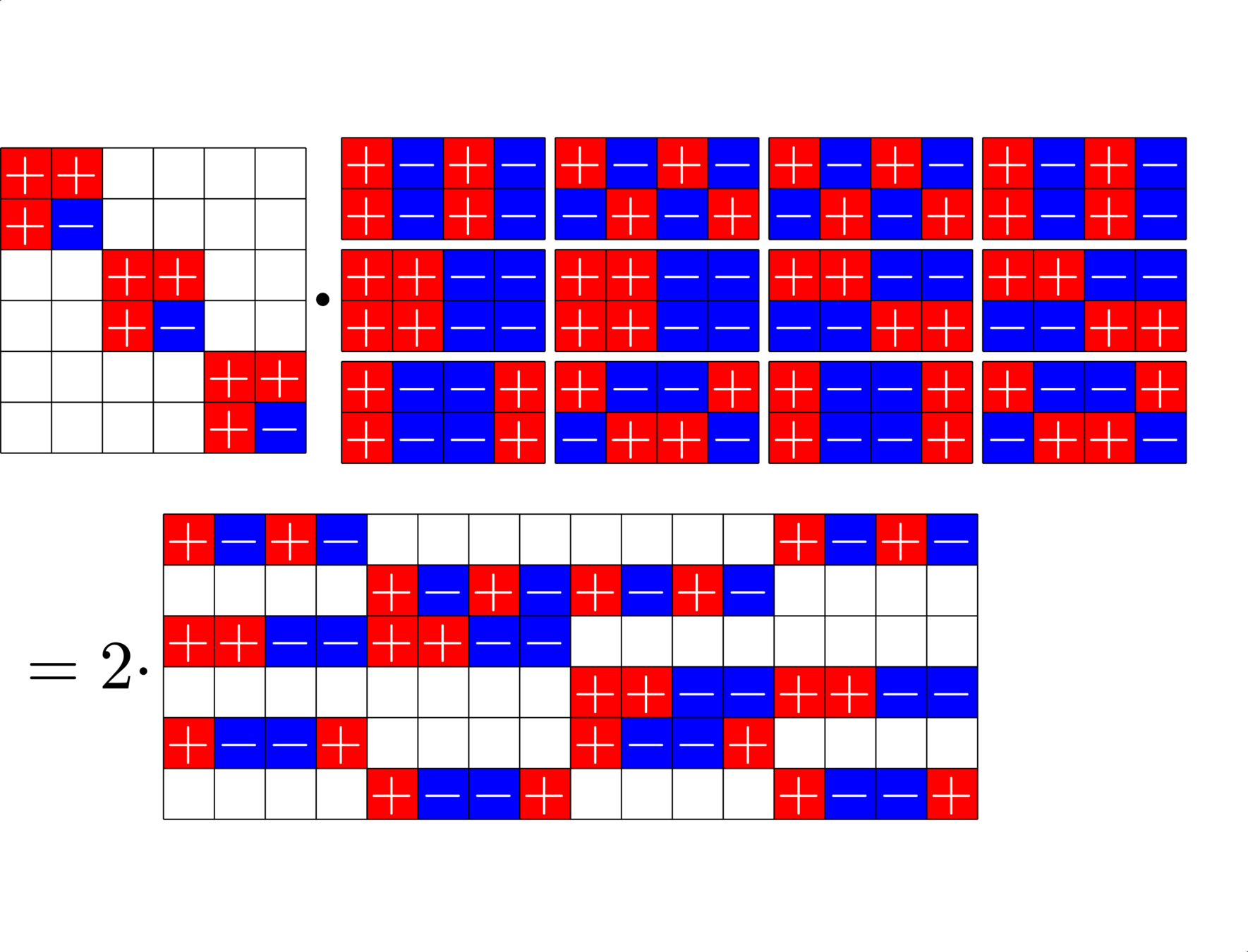
This \(6\times 16\) ETF from a McFarland difference set is also a Steiner ETF
Our second species: Tremain ETFs






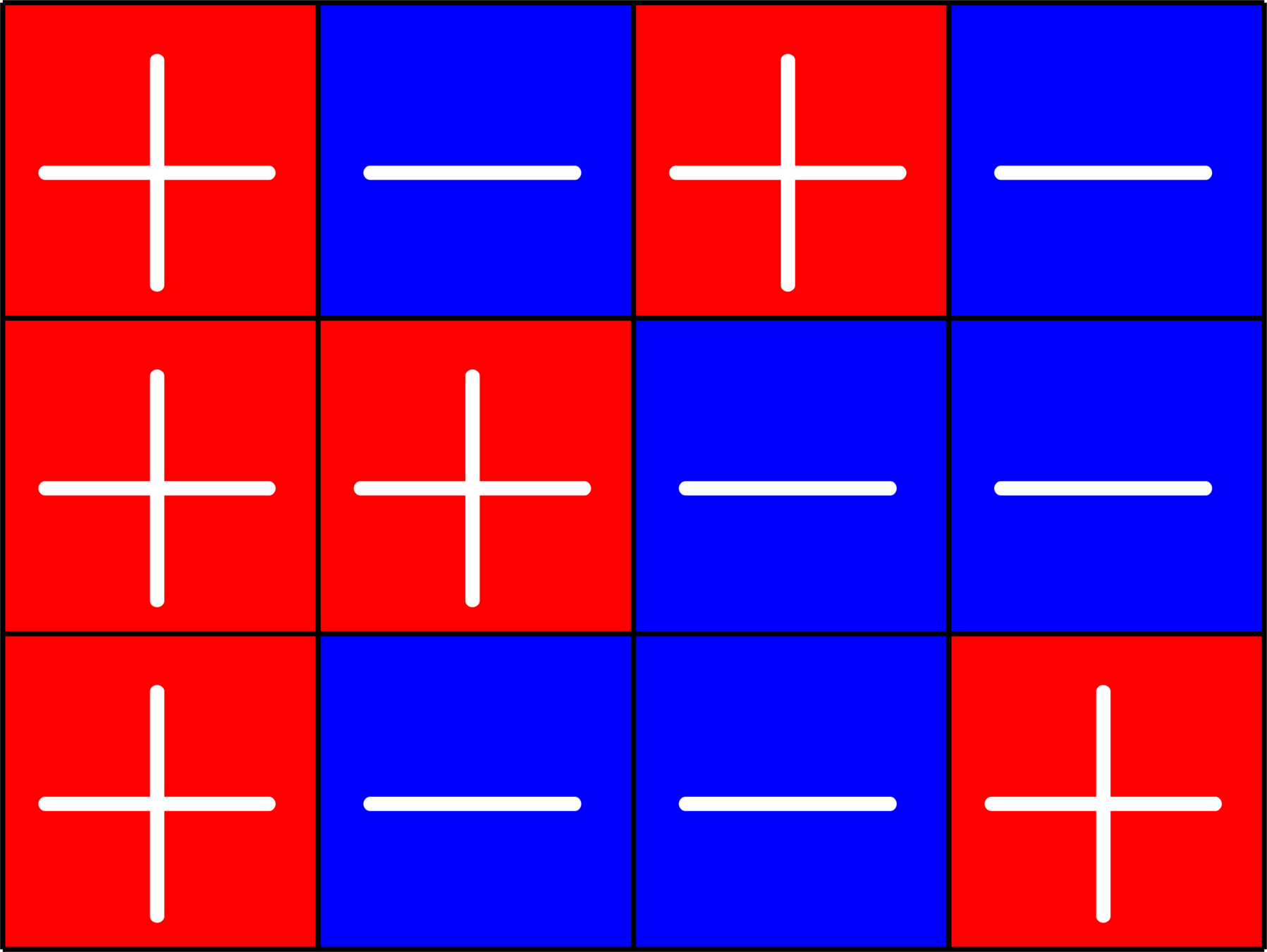
\(\ =+1\)
\(\ =-1\)
\(\ =\sqrt{2}\)
\(\ =-\sqrt{\dfrac{1}{2}}\)
\(\ =+\sqrt{\dfrac{1}{2}}\)
\(\ =\sqrt{\dfrac{3}{2}}\)
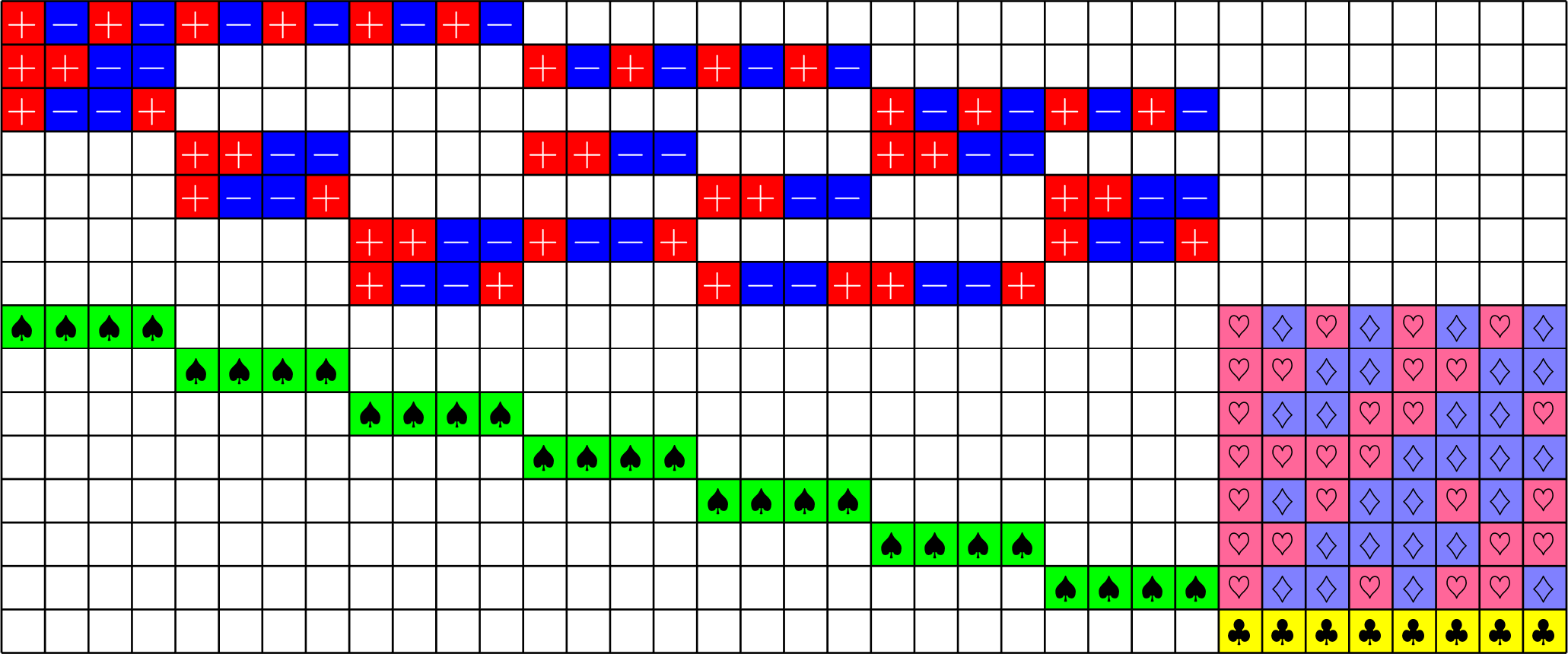
Our second species: Tremain ETFs




\[\left[\begin{array}{l} \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \end{array}\right.\]
\[\left.\begin{array}{l} \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \end{array}\right]\]

\(\bigotimes\)

\(\sqrt{2}\)
\(\sqrt{\dfrac{1}{2}}\)
\(\sqrt{\dfrac{3}{2}}\)


Hadamard matrix
Hadamard matrix
Steiner Triple System
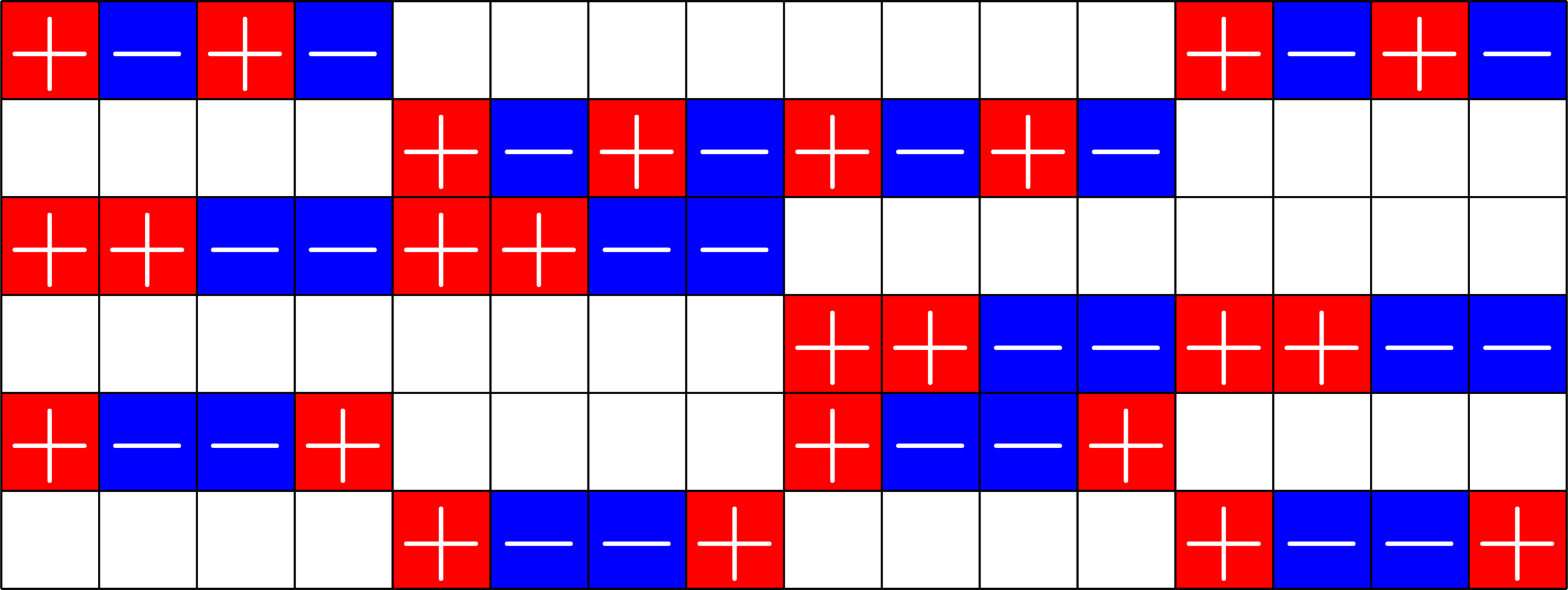
Tremain ETFs:
Theorem (Fickus, J,Mixon, Peterson '18). If there exists an
\(h\times h\) Hadamard matrix with \(h\equiv 1\) or \(2\) \(\text{mod}\ 3\),
then there exists a \((2,3,2h-1)\)-Steiner system
and by the Tremain construction there exists a real \(d\times N\) ETF where \[d=\frac{1}{3}(h+1)(2h+1),\qquad N=h(2h+1).\]




\(=-1\)
\(=-\sqrt{\frac{1}{2}}\)
\(=+1\)
\(=0\)

\(=\sqrt{\frac{1}{2}}\)
\(=\sqrt{\frac{1}{2}}\)
\(=\sqrt{\frac{3}{2}}\)
\(=\sqrt{2}\)
\(51\times 136\) Tremain ETF


What species is this?
*ETF table by Dustin Mixon and Matt Fickus
, Spence difference set
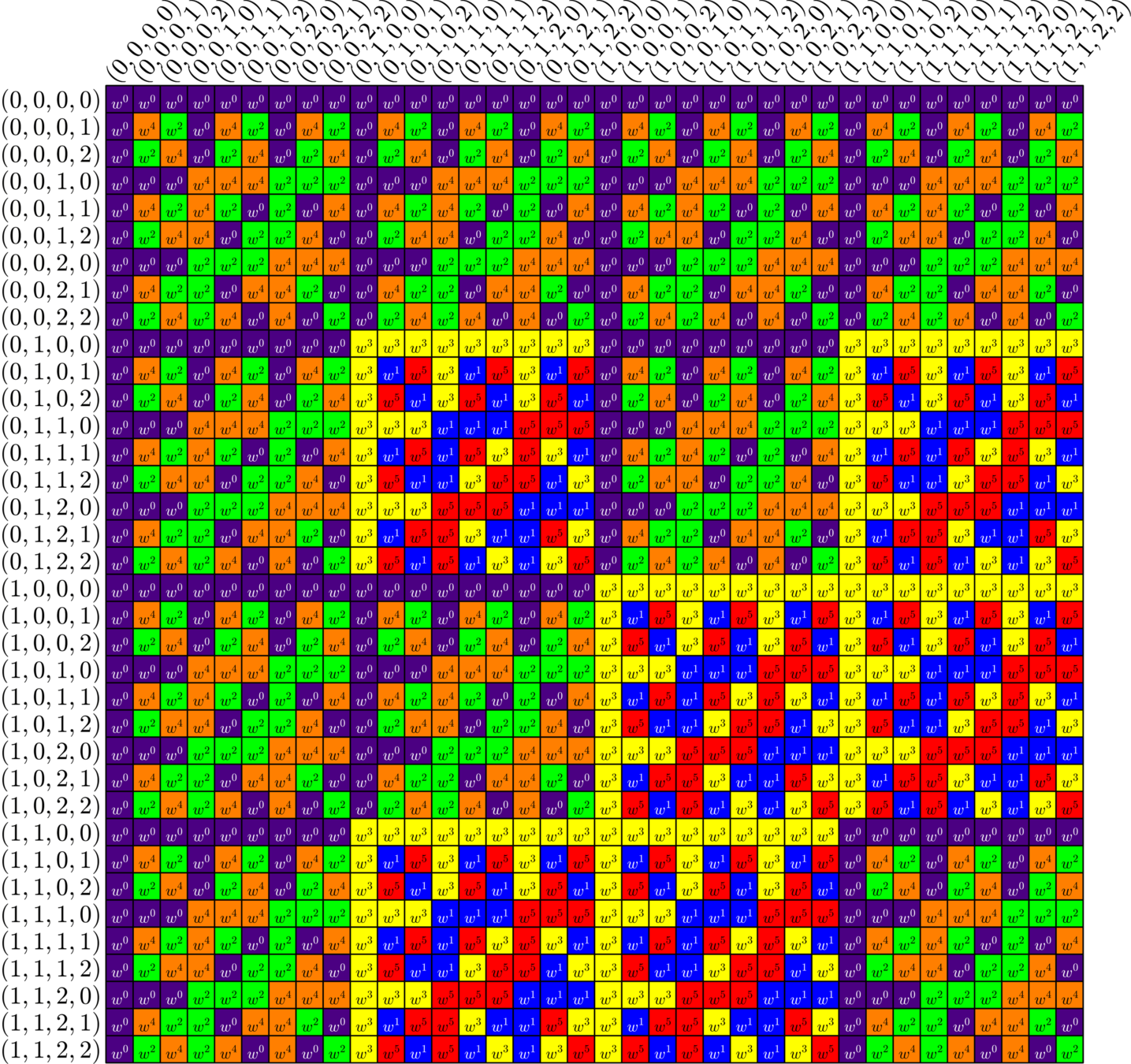
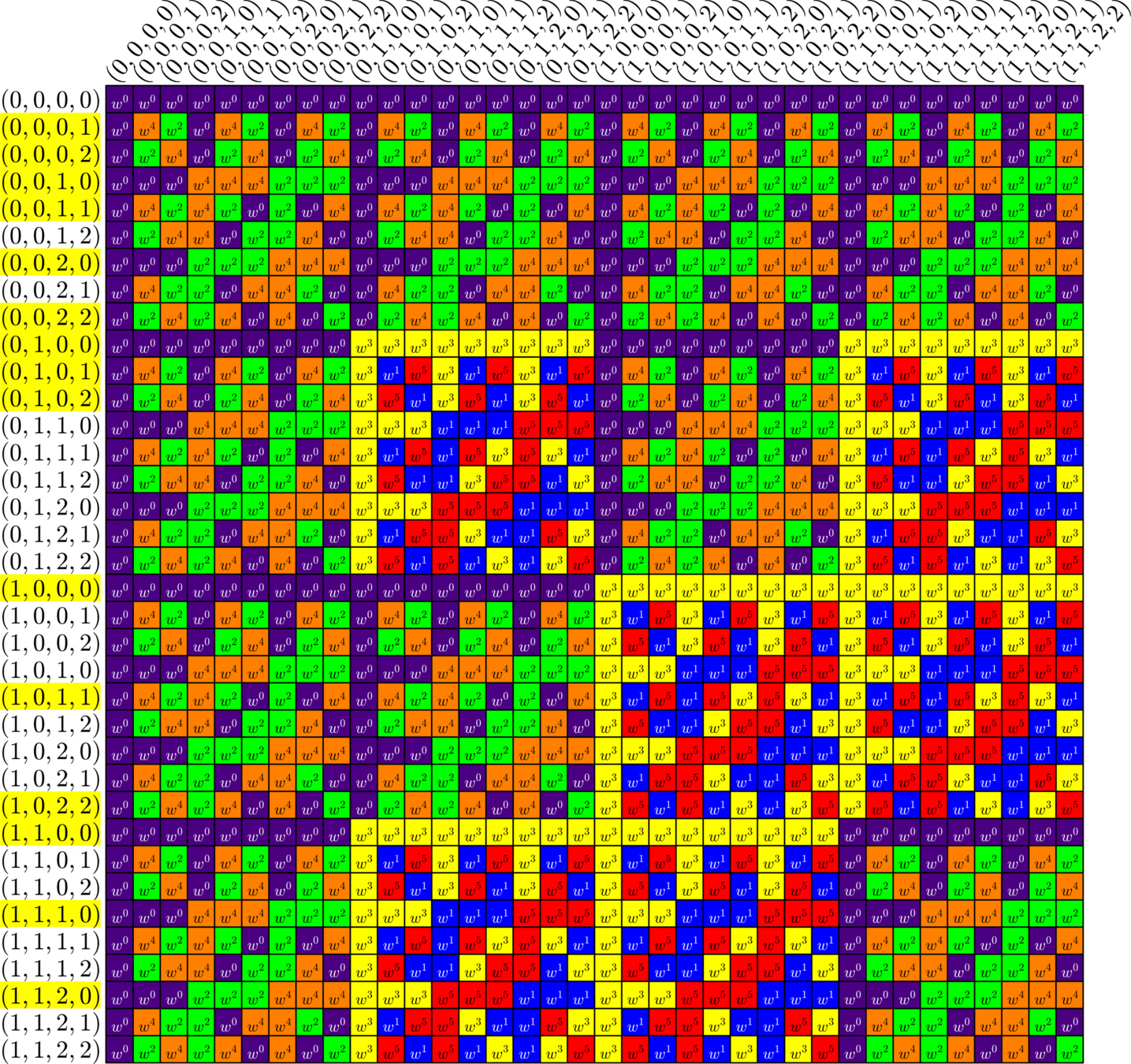


\(\bigotimes\)

\[\left[\begin{array}{l} \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \end{array}\right.\]
\[\left.\begin{array}{l} \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \end{array}\right]\]

\[\cong\]
Unitary transformation
\(I_{3}\otimes\)(\(2\times 3\) ETF)
Hadamard Matrix
Group Divisible Design (GDD)
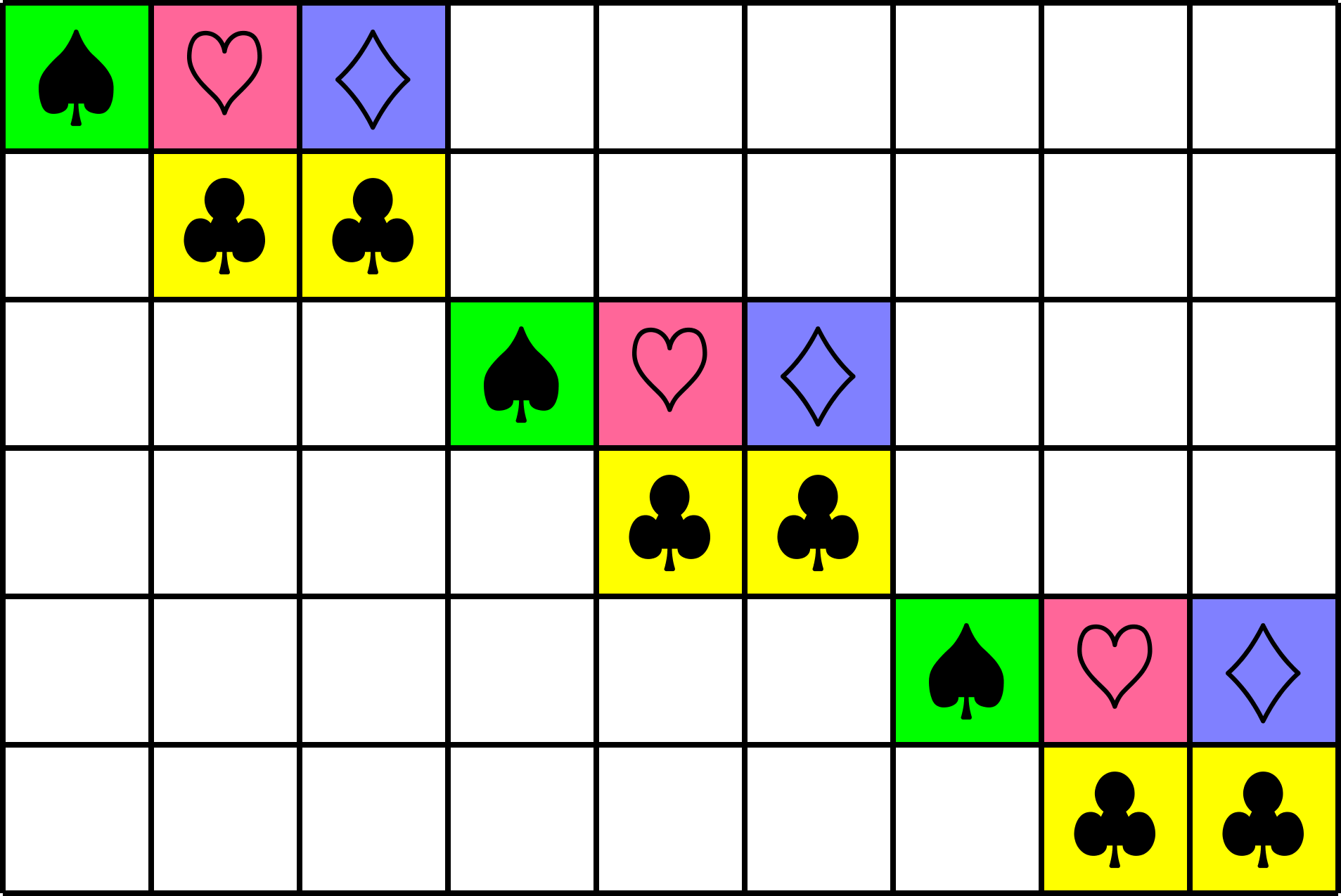
GDD ETF:
Tremain ETF:
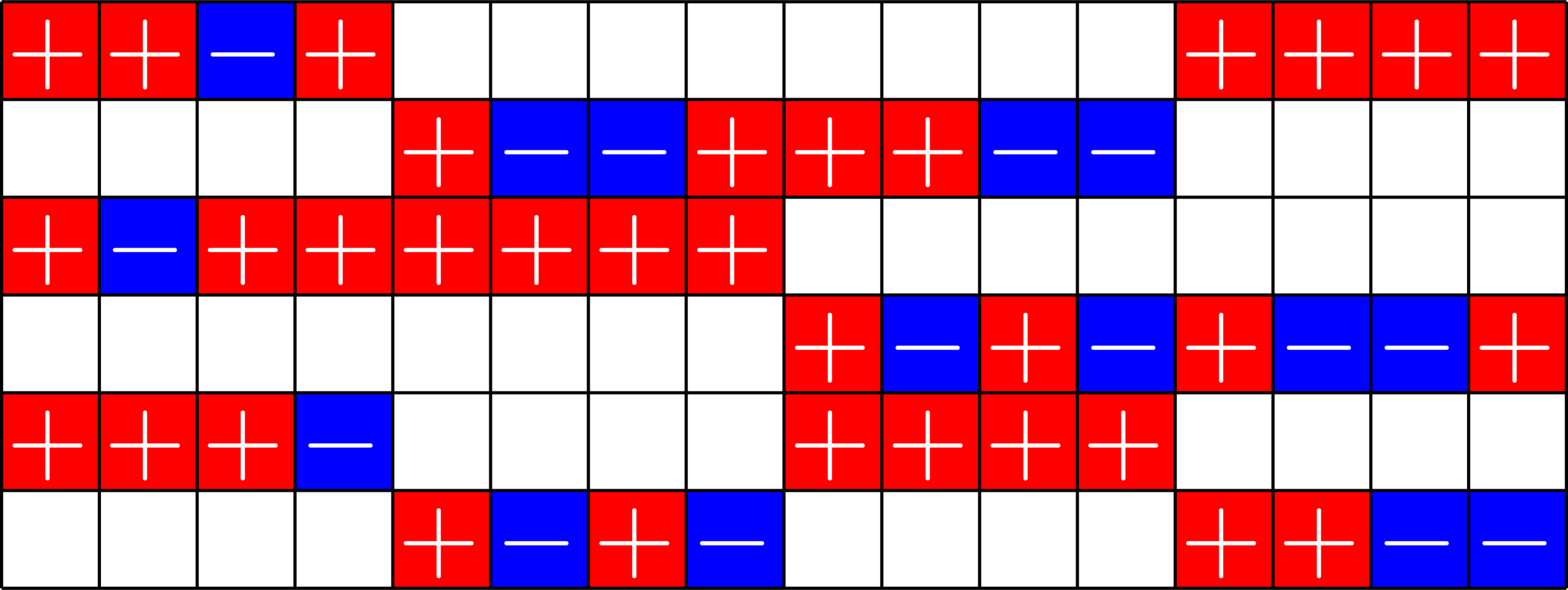
A New Species!
ETFs from GDDs
Theorem (Fickus, JJ '19). Given a
\(d\times n\) ETF

\(k\)-GDD of type \(M^{U}\)
and
provided certain integrality conditions hold, there exists a \(D\times N\) ETF with \(D>d\), \(N>n\) and \(\frac{D}{N}\approx \frac{d}{n}.\)

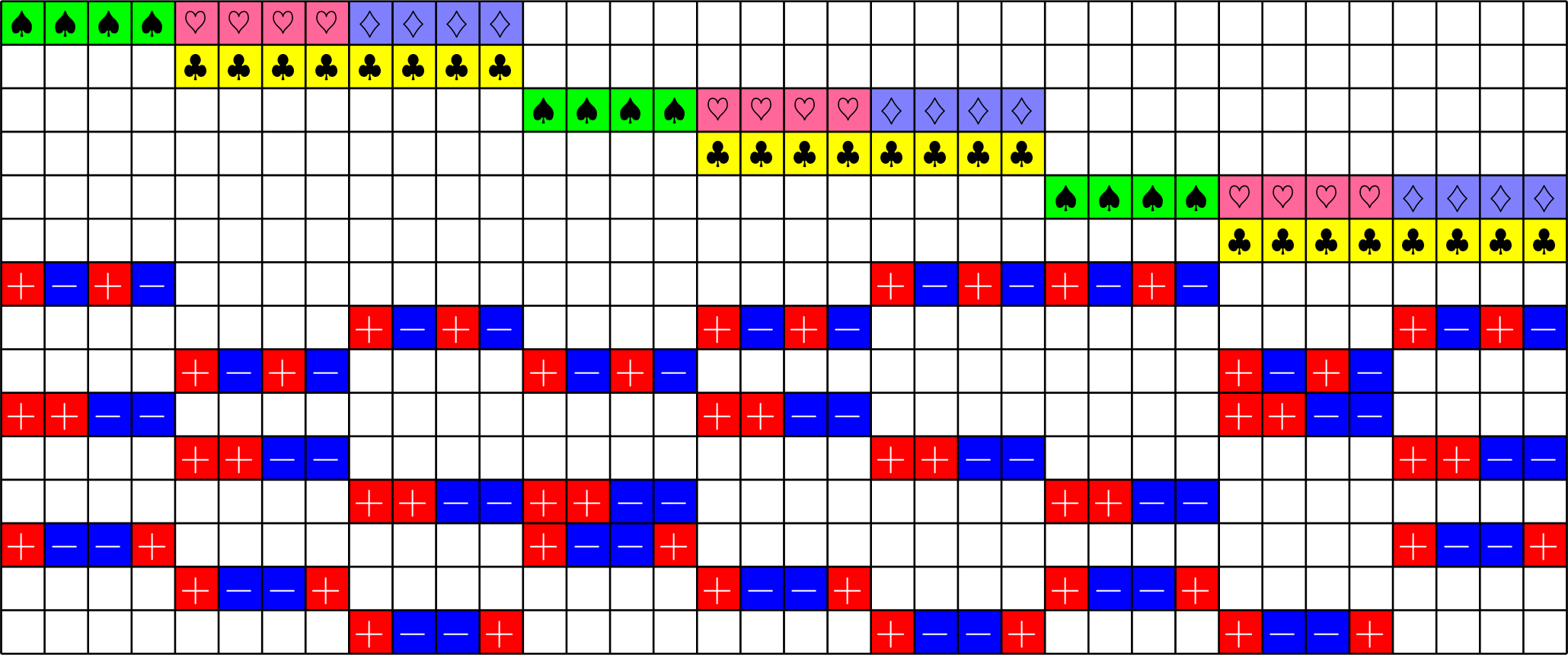
A New ETF
This GDD
Combined with a \(6\times 16\) ETF, like this one:

produces a complex \(266\times 1008\) ETF, which appears to be new!
Real ETFs and Graphs

\(\Phi=\)
- Given a real ETF \(\Phi\)
- Normalize so that all dot products with the first vector are positive.
Real ETFs and Graphs
\(\Phi^{\top}\Phi=\)
- Given a real ETF \(\Phi\)
- Normalize so that all dot products with the first vector are positive.
- Look at the gram matrix \(\Phi^{\top}\Phi\)
Real ETFs and Graphs
- Given a real ETF \(\Phi\)
- Normalize so that all dot products with the first vector are positive.
- Look at the gram matrix \(\Phi^{\top}\Phi\)
- Remove the first row and column and zero out the diagonal
- This is the Seidel adjacency matrix of a strongly regular graph

Real ETFs and Graphs
- Given a real ETF \(\Phi\)
- Normalize so that all dot products with the first vector are positive.
- Look at the gram matrix \(\Phi^{\top}\Phi\)
- Remove the first row and column and zero out the diagonal
- This is the Seidel adjacency matrix of a strongly regular graph


Real ETFs and Graphs
A. E. Brouwer maintains a table of known strongly regular graphs at
https://www.win.tue.nl/~aeb/graphs/srg/srgtab.html
or
The Handbook of Combinatorial Designs

Moreover, if
- \(\mathbf{1} := [1\ \ 1\ \ \cdots\ \ 1]\) is in the row space of \(\Phi\), or
- \(\mathbf{1}^{\top}\) is in \(\ker\Phi\)
Then there the off-diagonal of \(\Phi^{\top}\Phi\) is already the Seidel adjacency matrix of an SRG. No normalization step required!

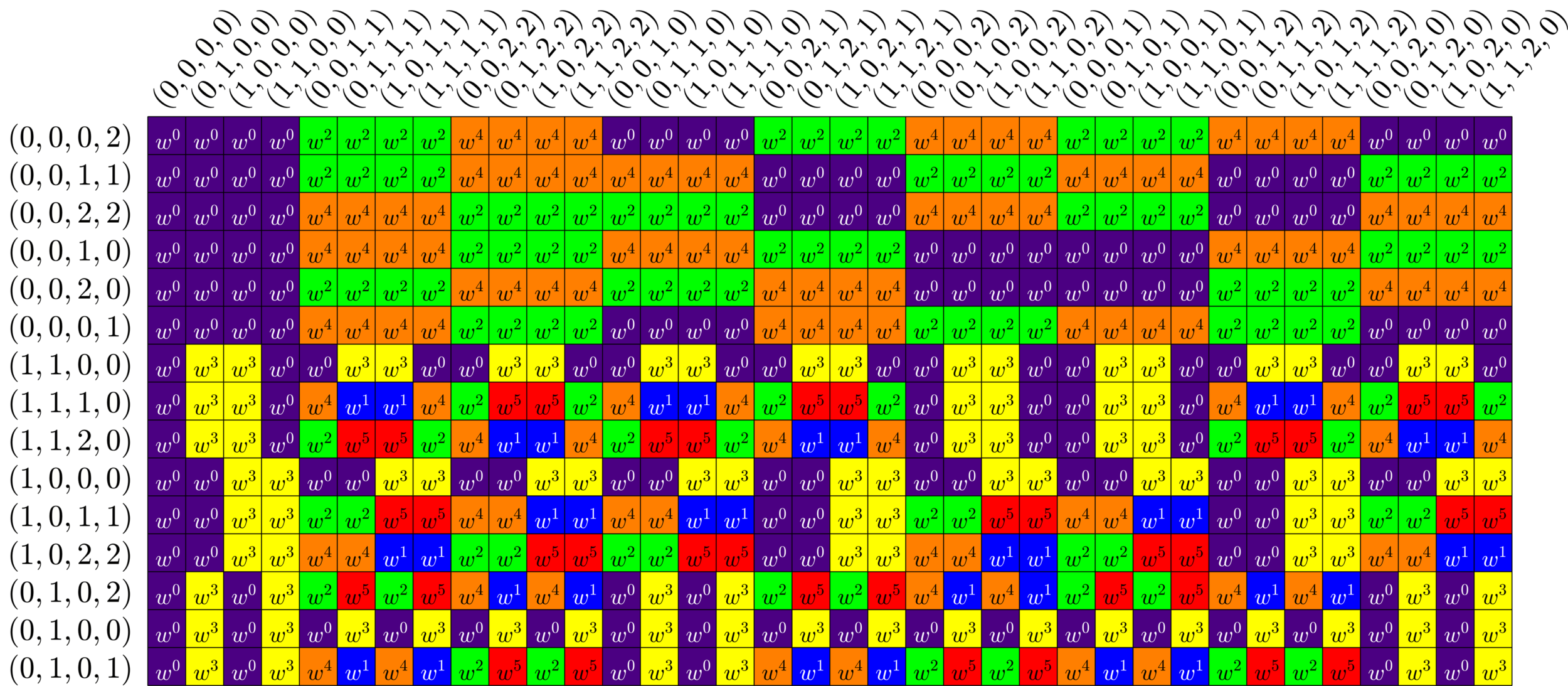
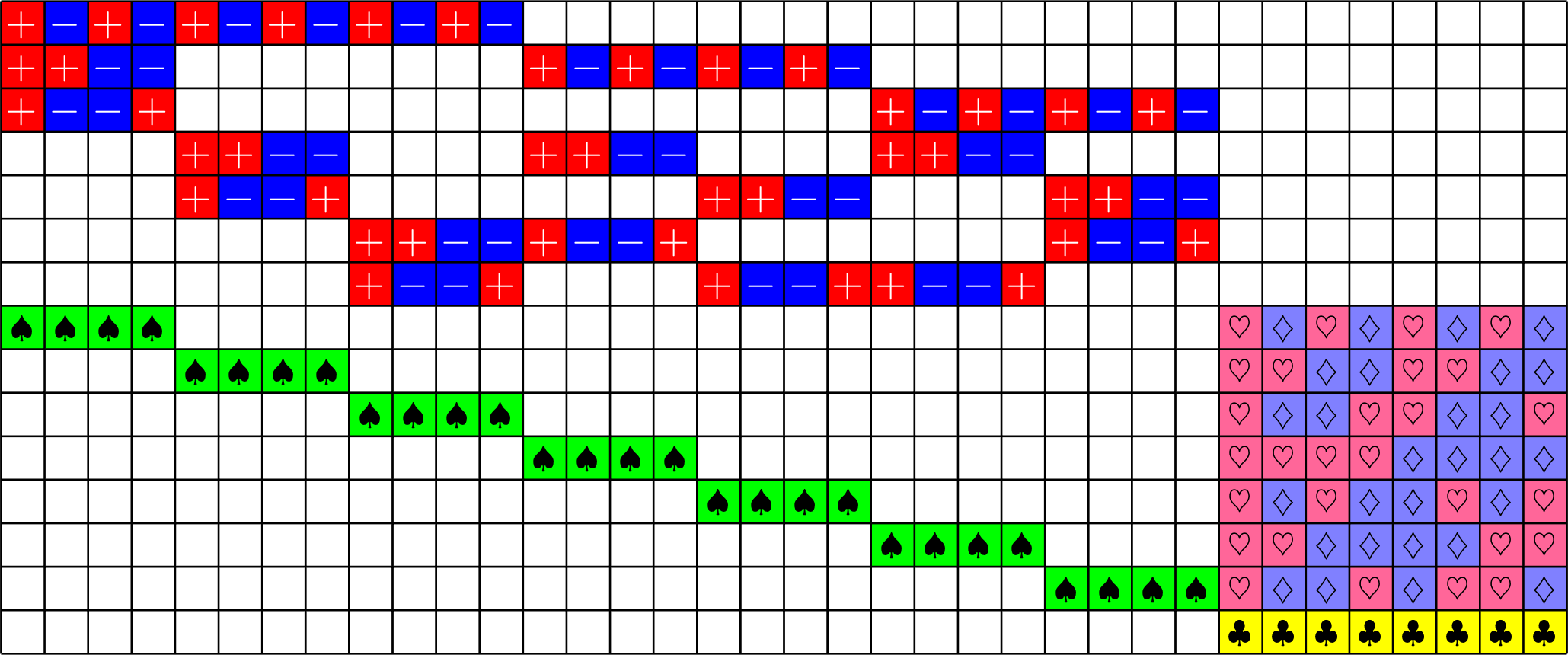
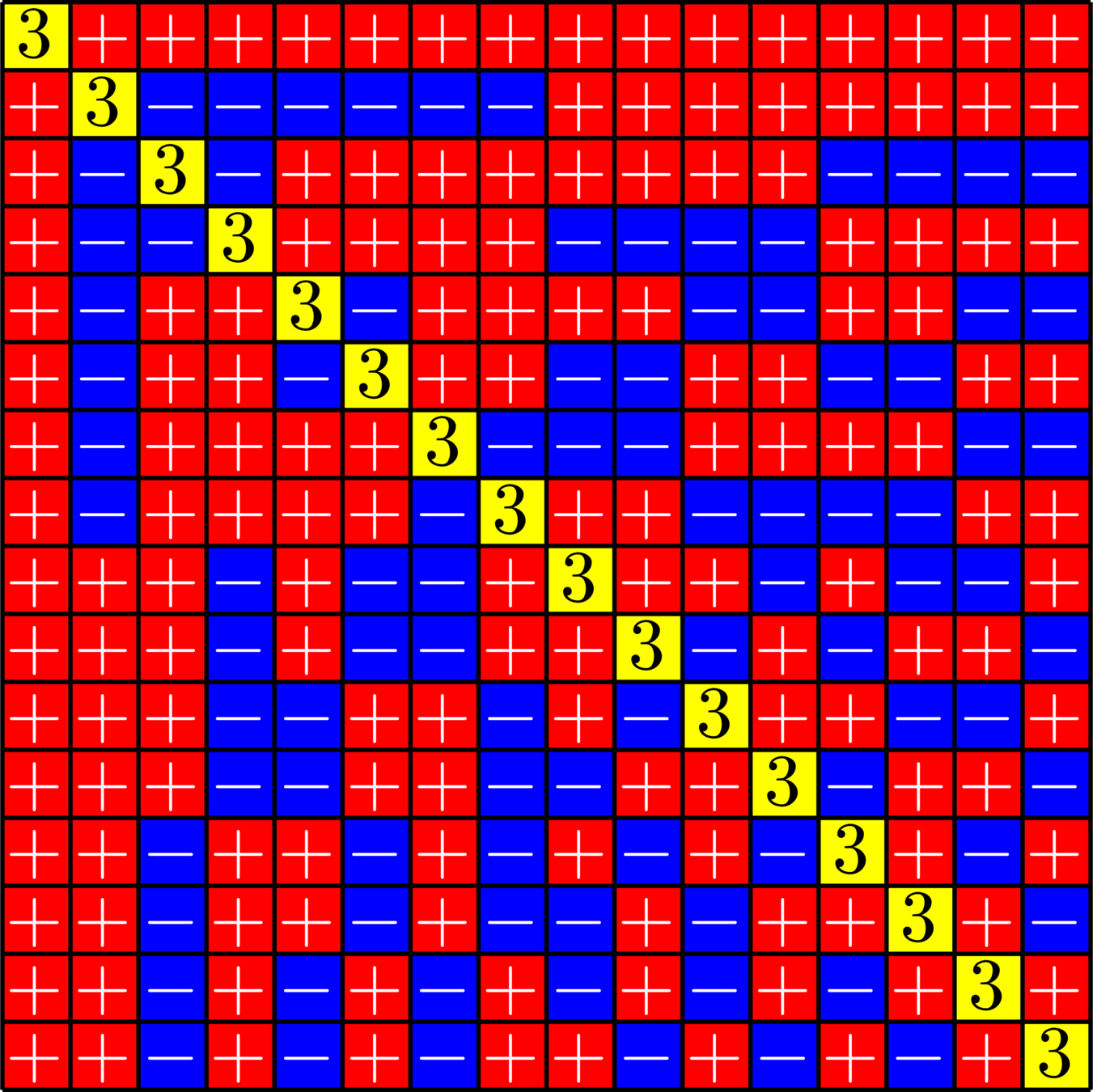
The Bible



These are the graphs associated with a real \(6\times 16\) ETF.

Every real \(6\times 16\) ETF is of the "Steiner species"
The Bible



These are the graphs associated with a real \(15\times 36\) ETF.
\(NO_{6}^{-}(2)\)






\(\ =+1\)
\(\ =-1\)
\(\ =\sqrt{2}\)
\(\ =-\sqrt{\dfrac{1}{2}}\)
\(\ =+\sqrt{\dfrac{1}{2}}\)
\(\ =\sqrt{\dfrac{3}{2}}\)


\(\ =-\sqrt{2}\)
\(\ =-\sqrt{\dfrac{3}{2}}\)
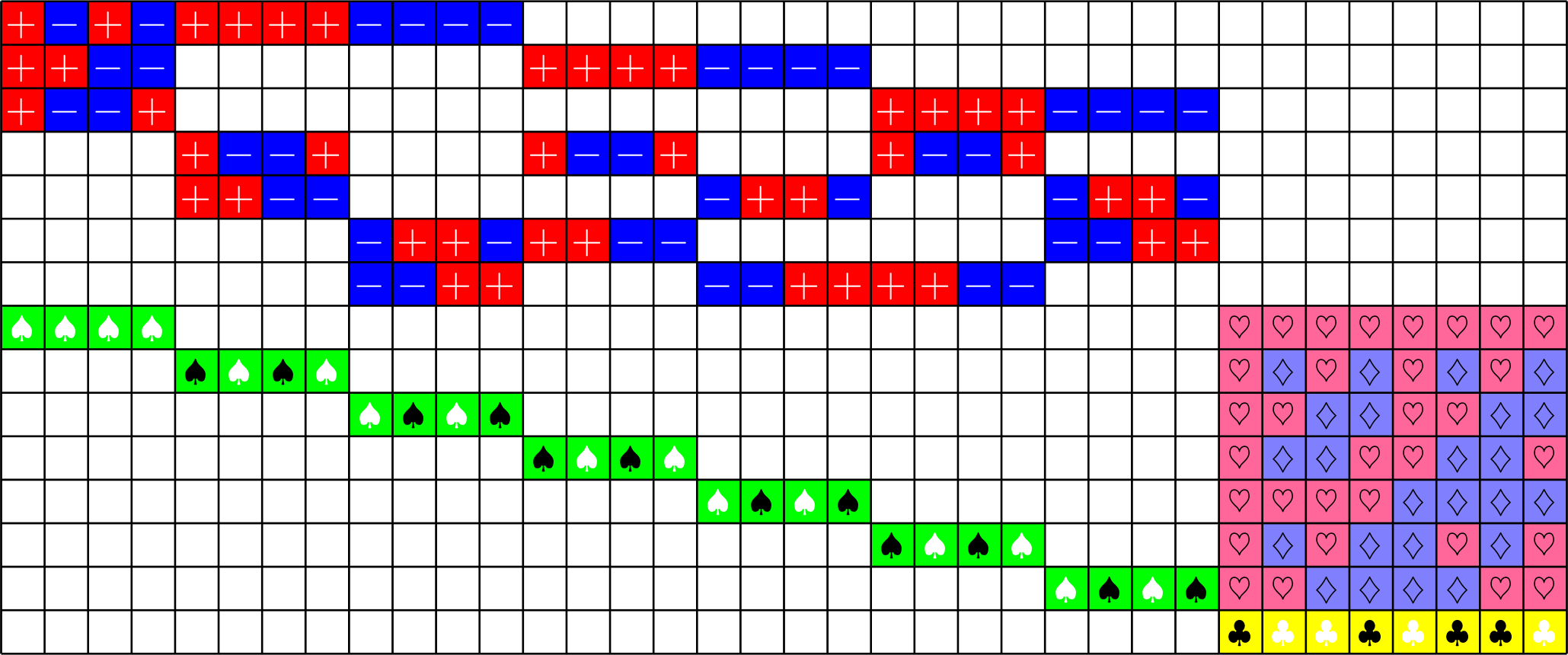
\(NO_{6}^{-}(2)\)

- \(NO_{6}^{2}\) is a Tremain ETF, not a new species.
- \(\mathbf{1} = [1\ 1\ \cdots\ 1]^{\top}\) is in the kernel.
- This gives us a strongly regular graph on 36 vertices.
- This can be generalized to all other Tremain ETFs.
Centered Tremain ETFs:
Theorem (J, '21). If there exists an
\(h\times h\) Hadamard matrix with \(h\equiv 1\) or \(2\) \(\text{mod}\ 3\),
then there exists a strongly regular graph with parameters:
\[v=h(2h+1),\quad k=h^2-1,\quad \lambda=\frac{1}{2}(h^2-4),\quad \mu = \frac{1}{2}h(h-1)\]


There exists a \(20\times 20\) Hadamard matrix, and hence an SRG(820,399,198,190), which is new!
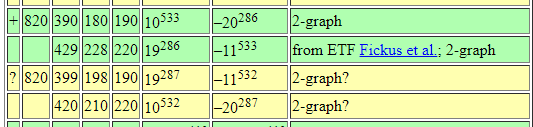
From Brouwer's table online:
Thanks!
- This work was partially supported by NSF #1830066
- Webpage: https://sites.google.com/view/john-jasper-math/home
- Slides: https://slides.com/johnjasper

JMM 2022
By John Jasper
JMM 2022
- 584



