Day 18:

Orthogonal projections and Gram-Schmidt 2

Theorem (the Cauchy-Schwarz inequality). Suppose \(V\) is an inner product space. If \(v,w\in V\), then

\[|\langle v,w\rangle|\leq \|v\|\|w\|.\]

Moreover, if equality occurs, then \(v\) and \(w\) are dependent.

Proof. If \(v=0\) then both sides of the inequality are zero, hence we are done. Moreover, note that \(v\) and \(w\) are dependent.

Suppose \(v\neq 0\). Define the scalar \(c = \frac{\langle v,w\rangle}{\|v\|^2}\), and compute

\[ \]

\[ = \|w\|^{2} - 2\frac{\langle v,w\rangle}{\|v\|^2}\langle w,v\rangle + \frac{|\langle v,w\rangle|^2}{\|v\|^4}\|v\|^{2}  = \|w\|^{2} - \frac{|\langle v,w\rangle|^2}{\|v\|^2}\]

\[0 \leq \|w-cv\|^{2} = \|w\|^{2} - 2\langle w,cv\rangle + \|cv\|^{2} = \|w\|^{2} - 2c\langle w,v\rangle + c^2\|v\|^{2}\]

Rearranging this inequality we have

\[\frac{|\langle v,w\rangle|^2}{\|v\|^2}\leq \|w\|^{2}.\]

Note, if this inequality is actually equality, then we have \(\|w-cv\|=0\), that is \(w-cv=0\). This implies \(v\) and \(w\) are dependent. \(\Box\)

Theorem (the Triangle inequality). Suppose \(V\) is an inner product space. If \(v,w\in V\), then

\[\|v+w\|\leq \|v\|+\|w\|.\]

Moreover, if equality occurs, then \(v\) and \(w\) are dependent.

Proof. First, note that \(\langle v,w\rangle\leq |\langle v,w\rangle|\). Using the polarization identity and the Cauchy-Schwarz inequality we have

 

 

\[\leq \|v\|^{2} + 2\|v\|\|w\| + \|w\|^{2} = \big(\|v\|+\|w\|\big)^{2}.\]

\[\leq \|v\|^{2} + 2|\langle v,w\rangle| + \|w\|^{2}.\]

\[\|v+w\|^{2} = \|v\|^{2}+2\langle v,w\rangle + \|w\|^{2}\]

Note that if \(\|v+w\|=\|v\|+\|w\|\), then we must have

\[\|v\|^{2} + 2|\langle v,w\rangle| + \|w\|^{2} = \|v\|^{2} + 2\|v\|\|w\| + \|w\|^{2}\]

and thus \(|\langle v,w\rangle|=\|v\|\|w\|\). By the Cauchy-Schwarz inequality, this implies \(v\) and \(w\) are dependent. \(\Box\)

Quiz. 

1. For \(x,y\in\mathbb{R}^{2}\) such that \(\langle x,y\rangle = 2\) it _______________ holds that \(\|x\|=\|y\|=1\).
2. For \(x,y\in\mathbb{R}^{2}\) such that \(\langle x,y\rangle = 0\) it _______________ holds that \(|\langle x,y\rangle| = \|x\|\|y\|\).
3. For normalized \(x,y\in\mathbb{R}^{2}\) such that \(\|x+y\|^{2} = \|x\|^{2} + \|y\|^{2}\) it _______________ holds that \(|\langle x,y\rangle| = \|x\|\|y\|\).
4. For nonzero vectors \(x,y\in\mathbb{R}^{n}\) it _______________ holds that \(\|x+y\|^{2} = \|x\|^{2}+\|y\|^{2}\) and \(\|x+y\|=\|x\|+\|y\|\).

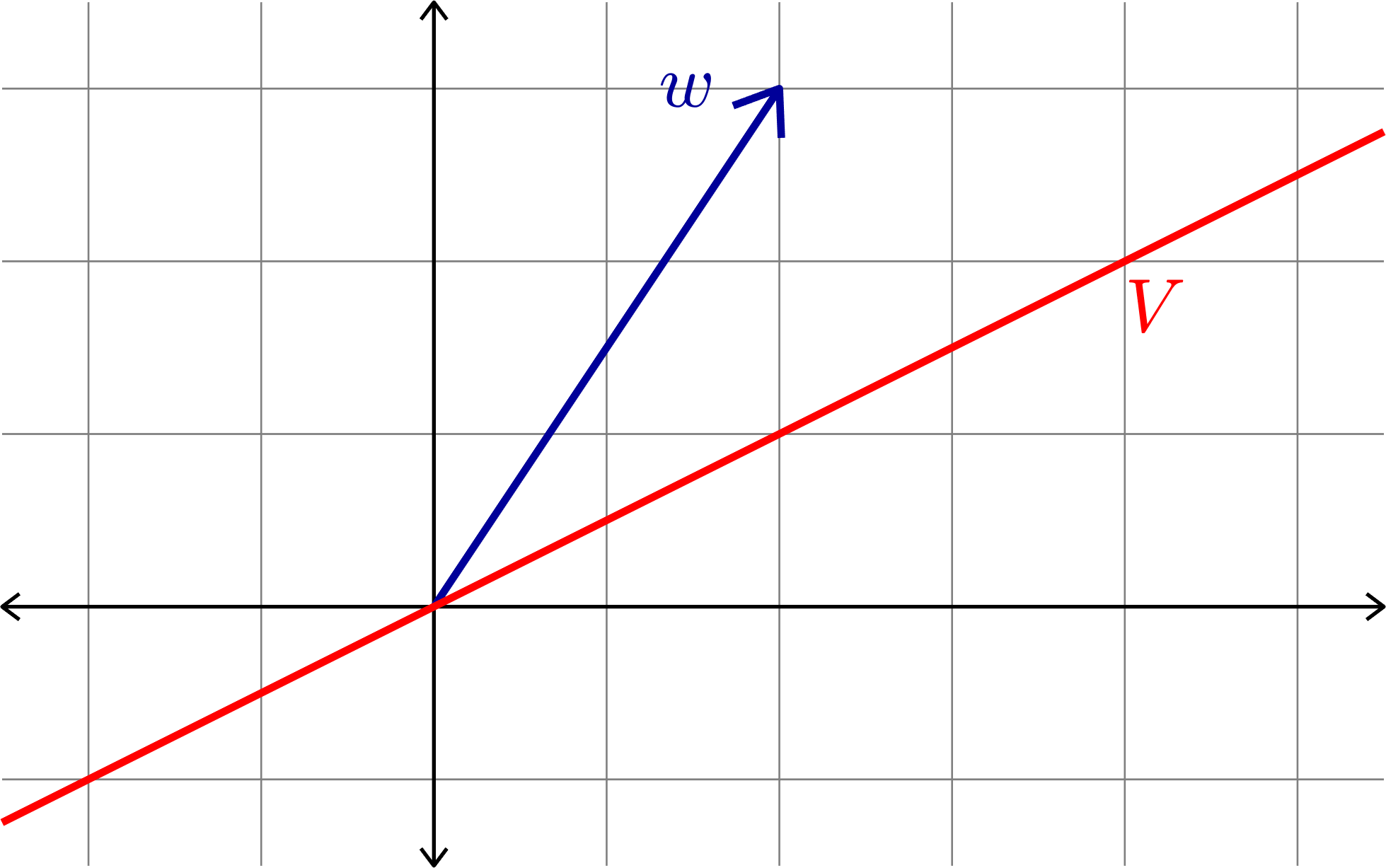
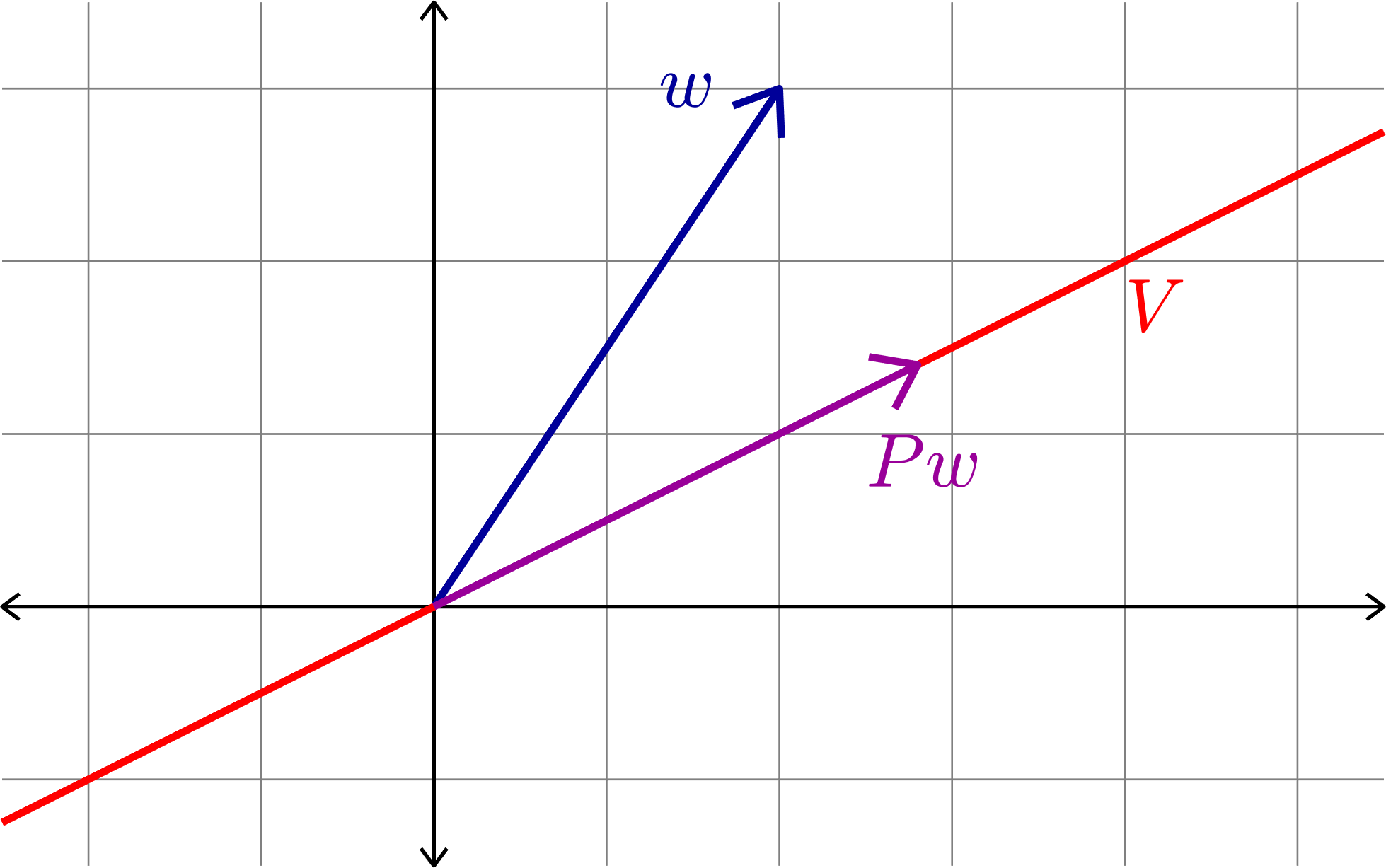
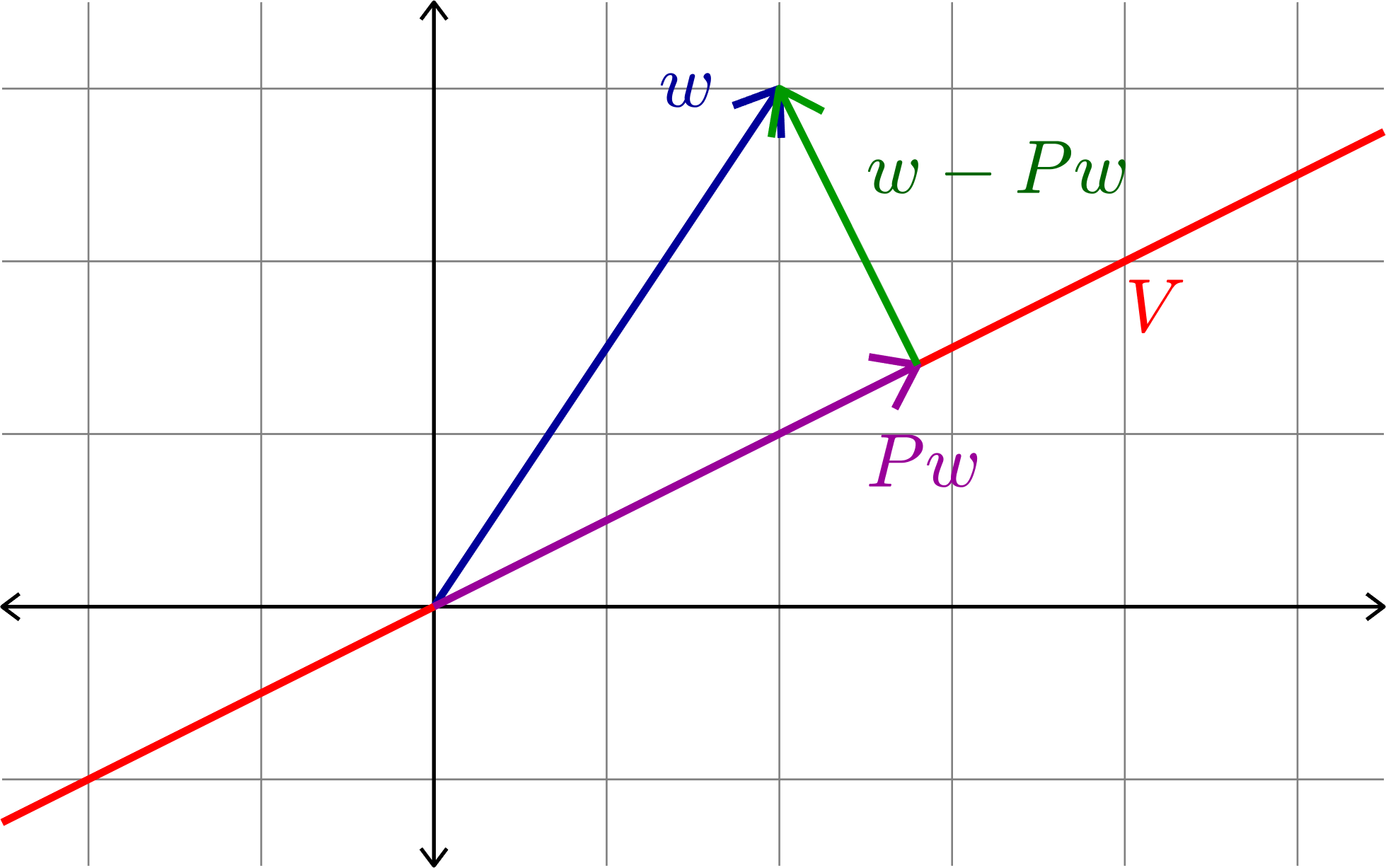
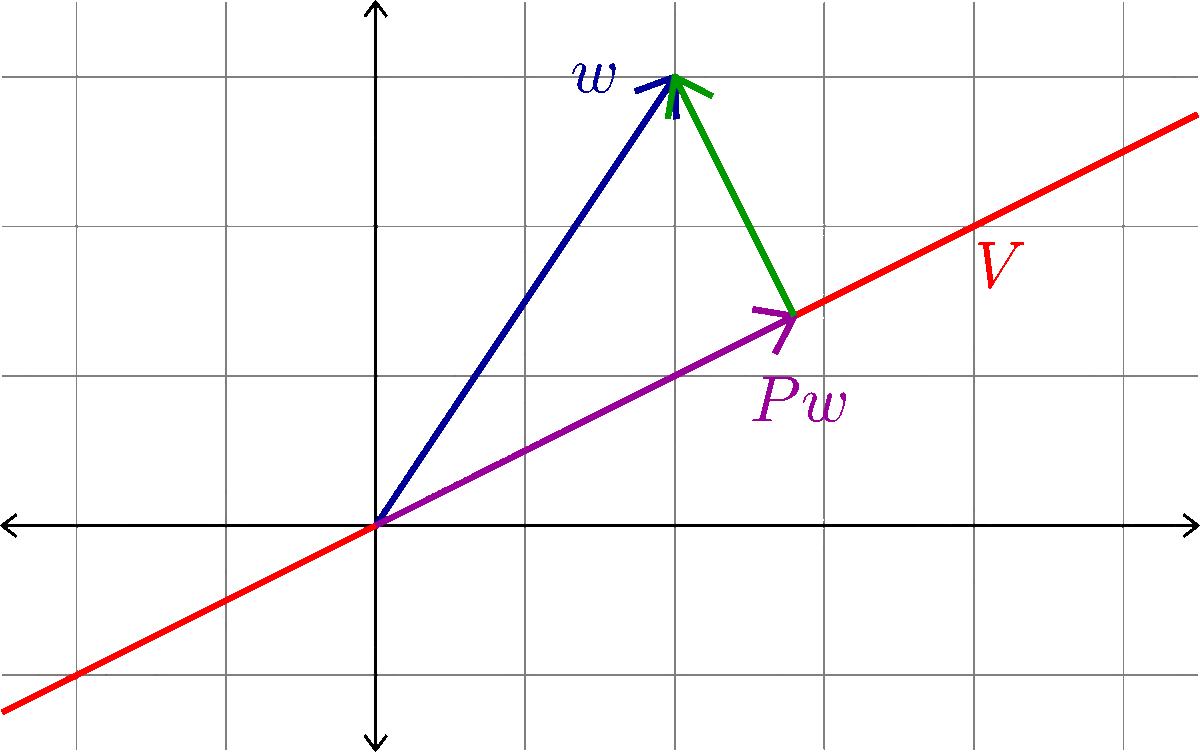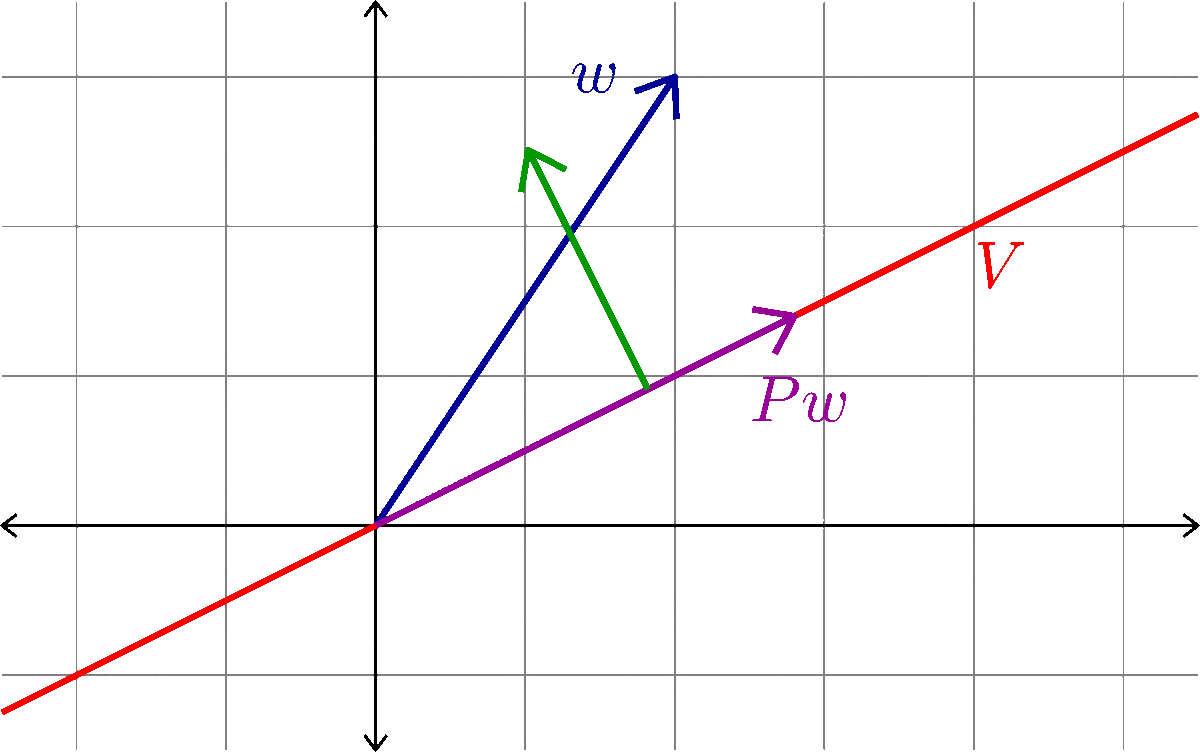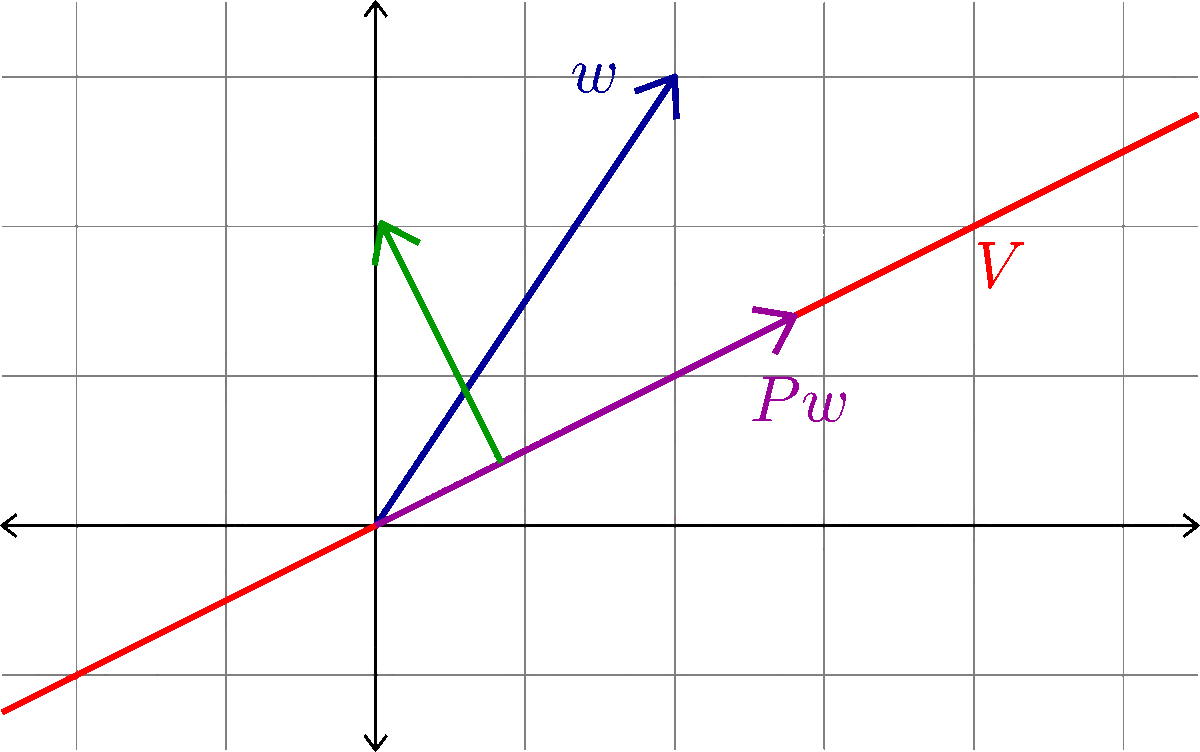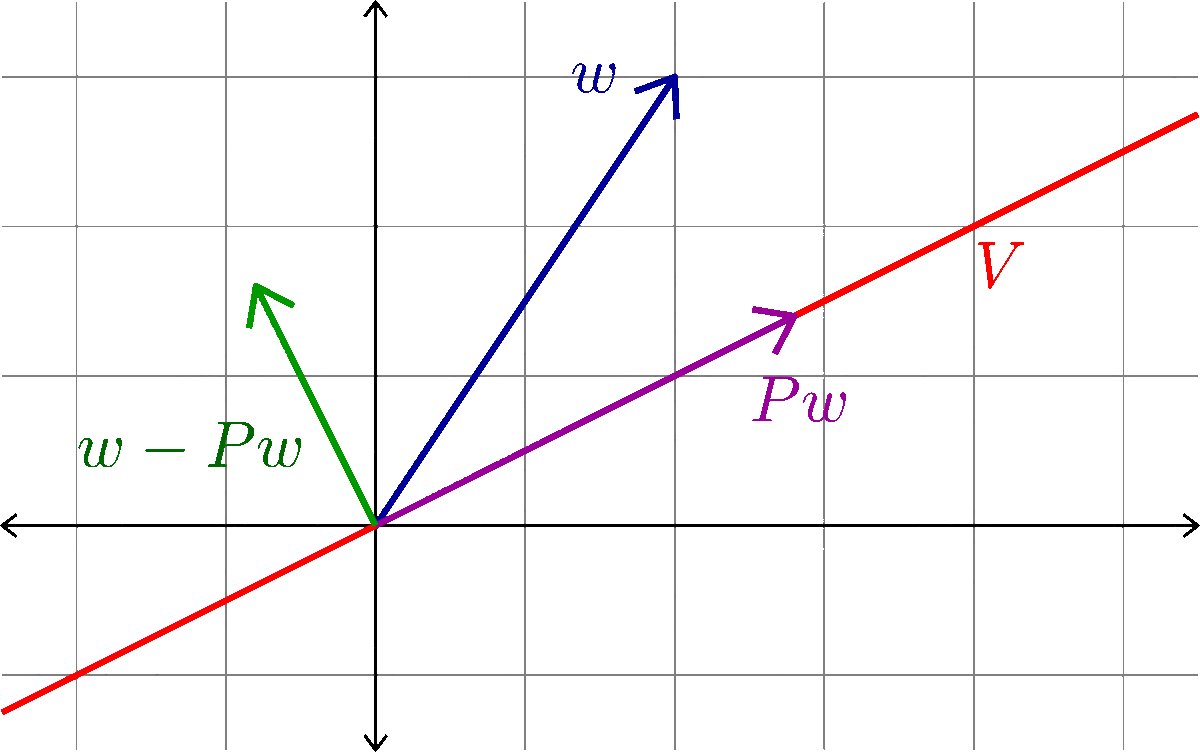
Orthogonal Projection

Given a subspace \(V\subset \R^{n}\) we want to define an orthogonal projection onto \(V\). That is, an \(n\times n\) matrix \(P\) with the following properties:

1. \(Pw\in V\) for all \(w\in\R^{n}\)
2. \(Pv=v\) for all \(v\in V\)
3. \(Pw\cdot (w-Pw)=0\) for all \(w\in\R^{n}\)

Orthogonal Projection

Example 1. If

\[V = \text{span}\left\{\begin{bmatrix} 1\\ 0\end{bmatrix}\right\}\]

then

\[P = \begin{bmatrix} 1 & 0\\ 0 & 0\end{bmatrix}\]

is the orthogonal projection onto \(V\).

1. If \(x = \begin{bmatrix} x_{1}\\ x_{2}\end{bmatrix}\in \R^{2}\), then \(Px = \begin{bmatrix} x_{1}\\ 0\end{bmatrix} = x_{1}\begin{bmatrix} 1\\ 0\end{bmatrix} \in V\)

2. If \(x\in V\), then \(x = \begin{bmatrix} x_{1}\\ 0\end{bmatrix}\) for some \(x_{1}\in\R\), then \(Px = \begin{bmatrix} x_{1}\\ 0\end{bmatrix} = x\)

Orthogonal Projection

Example 1 continued. 

3. Let \(w = \begin{bmatrix} w_{1}\\ w_{2}\end{bmatrix}\)

 

      \(Pw = \begin{bmatrix} w_{1}\\ 0\end{bmatrix}\)   and   \(w-Pw = \begin{bmatrix} w_{1}\\ w_{2}\end{bmatrix} - \begin{bmatrix} w_{1}\\ 0\end{bmatrix} = \begin{bmatrix} 0\\ w_{2}\end{bmatrix}\)

 

Thus,

\[Pw\cdot (w-Pw) = \begin{bmatrix} w_{1}\\ 0\end{bmatrix}\cdot \begin{bmatrix} 0\\ w_{2}\end{bmatrix} = w_{1}\cdot 0 + 0\cdot w_{2} = 0\]

Orthogonal Projection

Example 2. If

\[W = \text{span}\left\{\begin{bmatrix} 1\\ 1\\ 1\end{bmatrix}, \begin{bmatrix} 1\\ -1\\ 0\end{bmatrix}\right\}\]

then

\[Q = \frac{1}{6}\begin{bmatrix} 5 & -1 & 2\\ -1 & 5 & 2\\ 2 & 2 & 2\end{bmatrix}\]

is the orthogonal projection onto \(W\).

Note that

\(\dfrac{1}{6}\begin{bmatrix} 5 & -1 & 2\\ -1 & 5 & 2\\ 2 & 2 & 2\end{bmatrix}\begin{bmatrix} 1\\ 1\\ 1\end{bmatrix} = \begin{bmatrix} 1\\ 1\\ 1\end{bmatrix}\)    and    \(\dfrac{1}{6}\begin{bmatrix} 5 & -1 & 2\\ -1 & 5 & 2\\ 2 & 2 & 2\end{bmatrix}\begin{bmatrix} 1\\ -1\\ 0\end{bmatrix} = \begin{bmatrix} 1\\ -1\\ 0\end{bmatrix}\)

Orthogonal Projection

Example 2 continued.

If \(x\in W\), then \(x = a\begin{bmatrix} 1\\ 1\\ 1\end{bmatrix}+b\begin{bmatrix} 1\\ -1\\ 0\end{bmatrix}\) for some \(a,b\in\R\)

Thus

\(Qx = \dfrac{1}{6}\begin{bmatrix} 5 & -1 & 2\\ -1 & 5 & 2\\ 2 & 2 & 2\end{bmatrix}\left( a\begin{bmatrix} 1\\ 1\\ 1\end{bmatrix}+b\begin{bmatrix} 1\\ -1\\ 0\end{bmatrix}\right)\)

      \(= \dfrac{a}{6}\begin{bmatrix} 5 & -1 & 2\\ -1 & 5 & 2\\ 2 & 2 & 2\end{bmatrix} \begin{bmatrix} 1\\ 1\\ 1\end{bmatrix}+\dfrac{b}{6}\begin{bmatrix} 5 & -1 & 2\\ -1 & 5 & 2\\ 2 & 2 & 2\end{bmatrix} \begin{bmatrix} 1\\ -1\\ 0\end{bmatrix}\)

      \(= a\begin{bmatrix} 1\\ 1\\ 1\end{bmatrix}+b\begin{bmatrix} 1\\ -1\\ 0\end{bmatrix} = x\)

How to find an orthogonal projection matrix

Proposition. Assume \(V\subset\R^{n}\) is a subspace and \(\{v_{1},\ldots,v_{k}\}\) is an orthonormal basis for \(V\). If \[A = \begin{bmatrix} v_{1} & v_{2} & \cdots & v_{k}\end{bmatrix},\]

then the matrix \(P = AA^{\top}\) is the orthogonal projection onto \(V\).

Example. Let

\[V = \left\{\begin{bmatrix}a\\ b\\ c \end{bmatrix} : a+b = 0\right\}\quad\text{and}\quad \mathcal{B}= \left\{\frac{1}{\sqrt{2}}\begin{bmatrix}1\\ -1\\ 0 \end{bmatrix}, \begin{bmatrix}0\\ 0\\ 1 \end{bmatrix}\right\}.\]

Then it is easily checked that \(\mathcal{B}\) is an orthonormal basis for \(V\).

Set \[A = \begin{bmatrix} \frac{1}{\sqrt{2}} & 0\\ -\frac{1}{\sqrt{2}} & 0\\ 0 & 1\end{bmatrix},\]

then

\[P = AA^{\top} = \begin{bmatrix} \frac{1}{2} & -\frac{1}{2} & 0\\ -\frac{1}{2} & \frac{1}{2} & 0\\ 0 & 0 & 1\end{bmatrix}\]

is the orthogonal projection onto \(V\).

Gram-Schmidt

Assume \(V\) is a subspace and \(\{v_{1},\ldots,v_{k}\}\) is a basis for \(V\). 

 

First, we set

\[f_{1}: = \frac{1}{\|v_{1}\|} v_{1}.\]

Next we set

\[w_{2} = v_{2} - (f_{1}\cdot v_{2})f_{1} = v_{2} - f_{1}f_{1}^{\top}v_{2}\]

then we have

\[f_{1}^{\top} w_{2} = f_{1}^{\top} v_{2} - f_{1}^{\top}f_{1}f_{1}^{\top}v_{2}= f_{1}^{\top} v_{2} - \|f_{1}\|^{2} f_{1}^{\top}v_{2} = 0\]

We see that \(f_{1}\) and \(w_{2}\) are orthogonal, but \(\|w_{2}\|=\)???, so we set

\[f_{2}: = \frac{1}{\|w_{2}\|}w_{2}\]

and \(\{f_{1},f_{2}\}\) is an orthonormal set with the same span as \(\{v_{1},v_{2}\}\).

Gram-Schmidt

Now, we can assume we have an orthonormal set \(\{f_{1},\ldots,f_{j}\}\) with the same span as \(\{v_{1},\ldots,v_{j}\}\). Define

\[w_{j+1} = v_{j+1} - \sum_{i=1}^{j}f_{i}(f_{i}^{\top}v_{j+1}).\]

For any \(\ell\leq j\) we have \[f_{\ell}^{\top}w_{j+1} = f_{\ell}^{\top}v_{j+1} - \sum_{i=1}^{j}f_{\ell}^{\top}f_{i}(f_{i}^{\top}v_{j+1}) = f_{\ell}^{\top}v_{j+1} - f_{\ell}^{\top}v_{j+1} = 0.\] Hence, if we set \[f_{j+1} = \frac{1}{\|w_{j+1}\|}w_{j+1}\] then \(\{f_{1},f_{2},\ldots,f_{j+1}\}\) is an orthonormal set with the same span as  \(\{v_{1},\ldots,v_{j+1}\}\).

Continue until the \(k\)th step and we have an orthonormal basis \(\{f_{1},\ldots,f_{k}\}\) for \(V\).

Gram-Schmidt example 1

Find an orthonormal basis for \(N([1\ \ 1\ \ 1\ \ 1])\)

Note that \(\left\{\begin{bmatrix} -1\\ 1\\ 0\\ 0\end{bmatrix},\begin{bmatrix} -1\\ 0\\ 1\\ 0\end{bmatrix},\begin{bmatrix} -1\\ 0\\ 0\\ 1\end{bmatrix}\right\}\) is a basis for \(N([1\ \ 1\ \ 1\ \ 1])\)

Set \(f_{1} = \dfrac{1}{\sqrt{2}}\begin{bmatrix} -1\\ 1\\ 0\\ 0\end{bmatrix}\)

Set \(w_{2} = \begin{bmatrix} -1\\ 0\\ 1\\ 0\end{bmatrix} - \left(f_{1}\cdot\begin{bmatrix} -1\\ 0\\ 1\\ 0\end{bmatrix}\right) f_{1} = \begin{bmatrix} -1\\ 0\\ 1\\ 0\end{bmatrix} - \frac{1}{2}\begin{bmatrix} -1\\ 1\\ 0\\ 0\end{bmatrix} = \begin{bmatrix} -\frac{1}{2}\\ -\frac{1}{2}\\ 1\\ 0\end{bmatrix}\)

Set \(f_{2} = \dfrac{w_{2}}{\|w_{2}\|} = \frac{1}{\sqrt{6}}\begin{bmatrix} -1\\ -1\\ 2\\ 0\end{bmatrix}\)

Gram-Schmidt example 1

We already have \(e_{1} = \dfrac{1}{\sqrt{2}}\begin{bmatrix} -1\\ 1\\ 0\\ 0\end{bmatrix},\)  and \(e_{2} = \sqrt{\frac{2}{3}}\begin{bmatrix} -\frac{1}{2}\\ -\frac{1}{2}\\ 1\\ 0\end{bmatrix}\)

\(w_{3} = \begin{bmatrix} -1\\ 0\\ 0\\ 1\end{bmatrix} - \left(e_{1}\cdot \begin{bmatrix} -1\\ 0\\ 0\\ 1\end{bmatrix}\right) e_{1} - \left(e_{2}\cdot \begin{bmatrix} -1\\ 0\\ 0\\ 1\end{bmatrix}\right) e_{2}\)

\( = \begin{bmatrix} -1\\ 0\\ 0\\ 1\end{bmatrix} - \left(\frac{1}{\sqrt{2}}\right) \dfrac{1}{\sqrt{2}}\begin{bmatrix} -1\\ 1\\ 0\\ 0\end{bmatrix} - \left(\sqrt{\frac{2}{3}}\cdot \frac{1}{2}\right)  \sqrt{\frac{2}{3}}\begin{bmatrix} -\frac{1}{2}\\ -\frac{1}{2}\\ 1\\ 0\end{bmatrix} = \frac{1}{3}\begin{bmatrix} -1\\ -1\\ -1\\ 3\end{bmatrix}\)

\[e_{3}:=\frac{w_{3}}{\|w_{3}\|} = \frac{1}{2\sqrt{3}}\begin{bmatrix} -1\\ -1\\ -1\\ 3\end{bmatrix}\]

Gram-Schmidt example 1

The set \[\left\{\dfrac{1}{\sqrt{2}}\begin{bmatrix} -1\\ 1\\ 0\\ 0\end{bmatrix}, \frac{1}{\sqrt{6}}\begin{bmatrix} -1\\ -1\\ 2\\ 0\end{bmatrix},\frac{1}{2\sqrt{3}}\begin{bmatrix} -1\\ -1\\ -1\\ 3\end{bmatrix}\right\}\] is an orthonormal basis for \(N([1\ \ 1\ \ 1\ \ 1])\)

The set \[\left\{\begin{bmatrix} -1\\ 1\\ 0\\ 0\end{bmatrix}, \begin{bmatrix} -1\\ -1\\ 2\\ 0\end{bmatrix},\begin{bmatrix} -1\\ -1\\ -1\\ 3\end{bmatrix}\right\}\] is an orthogonal basis for \(N([1\ \ 1\ \ 1\ \ 1])\)

Gram-Schmidt Example 2

We wish to find an orthonormal basis for \(C(A)\) where

\[A = \begin{bmatrix} 1 & -1 & 1\\ 1 & 4 & 6\\ -1 & 3 & 1\\ 2 & -3 & 1\end{bmatrix}\]

First, we row reduce to find

\[\text{rref}(A) = \begin{bmatrix} 1 & 0 & 2\\ 0 & 1 & 1\\ 0 & 0 & 0\\ 0 & 0 & 0\end{bmatrix}.\]

This shows us that \(\{v_{1},v_{2}\}\) is a basis for \(C(A)\) where

\[v_{1} = \begin{bmatrix} 1\\ 1 \\ -1\\ 2 \end{bmatrix} \quad\text{and}\quad v_{2}=\begin{bmatrix} -1\\ 4\\ 3\\ -3\end{bmatrix}.\]

 

Gram-Schmidt Example 2

First, we set

\[f_{1} = \frac{1}{\sqrt{7}}\begin{bmatrix} 1\\ 1 \\ -1\\ 2 \end{bmatrix} = \begin{bmatrix} \frac{1}{\sqrt{7}}\\ \frac{1}{\sqrt{7}} \\ -\frac{1}{\sqrt{7}}\\ \frac{2}{\sqrt{7}} \end{bmatrix} \]

\[f_{1}^{\top}v_{2} = \frac{1}{\sqrt{7}}(-1 + 4 -3-6)=-\frac{6}{\sqrt{7}}\]

\[w_{1} = v_{2} - f_{1}(f_{1}^{\top}v_{2}) = \begin{bmatrix} -1\\ 4\\ 3\\ -3 \end{bmatrix}+\frac{6}{\sqrt{7}}\left(\frac{1}{\sqrt{7}}\begin{bmatrix} 1\\ 1 \\ -1\\ 2 \end{bmatrix}\right) = \begin{bmatrix} -\frac{1}{7}\\ \frac{34}{7}\\ \frac{15}{7}\\ -\frac{9}{7}\end{bmatrix} = \frac{1}{7}\begin{bmatrix} -1\\ 34\\ 15\\ -9\end{bmatrix}\]

\[f_{2} = \frac{w_{2}}{\|w_{2}\|} = \frac{1}{\sqrt{1463}}\begin{bmatrix} -1\\34\\ 15\\ -9\end{bmatrix}\]

Gram-Schmidt Example 2

The set

\[\left\{\frac{1}{\sqrt{7}}\begin{bmatrix} 1\\ 1 \\ -1\\ 2 \end{bmatrix}, \frac{1}{\sqrt{1463}}\begin{bmatrix} -1\\34\\ 15\\ -9\end{bmatrix}\right\}\] is an orthonormal basis for \(C(A)\).

 

The set

\[\left\{\begin{bmatrix} 1\\ 1 \\ -1\\ 2 \end{bmatrix},\begin{bmatrix} -1\\34\\ 15\\ -9\end{bmatrix}\right\}\] is an orthogonal basis for \(C(A)\).