Diagonals of Compact Operators

John Jasper

        South Dakota State University

The Pythagorean Theorem

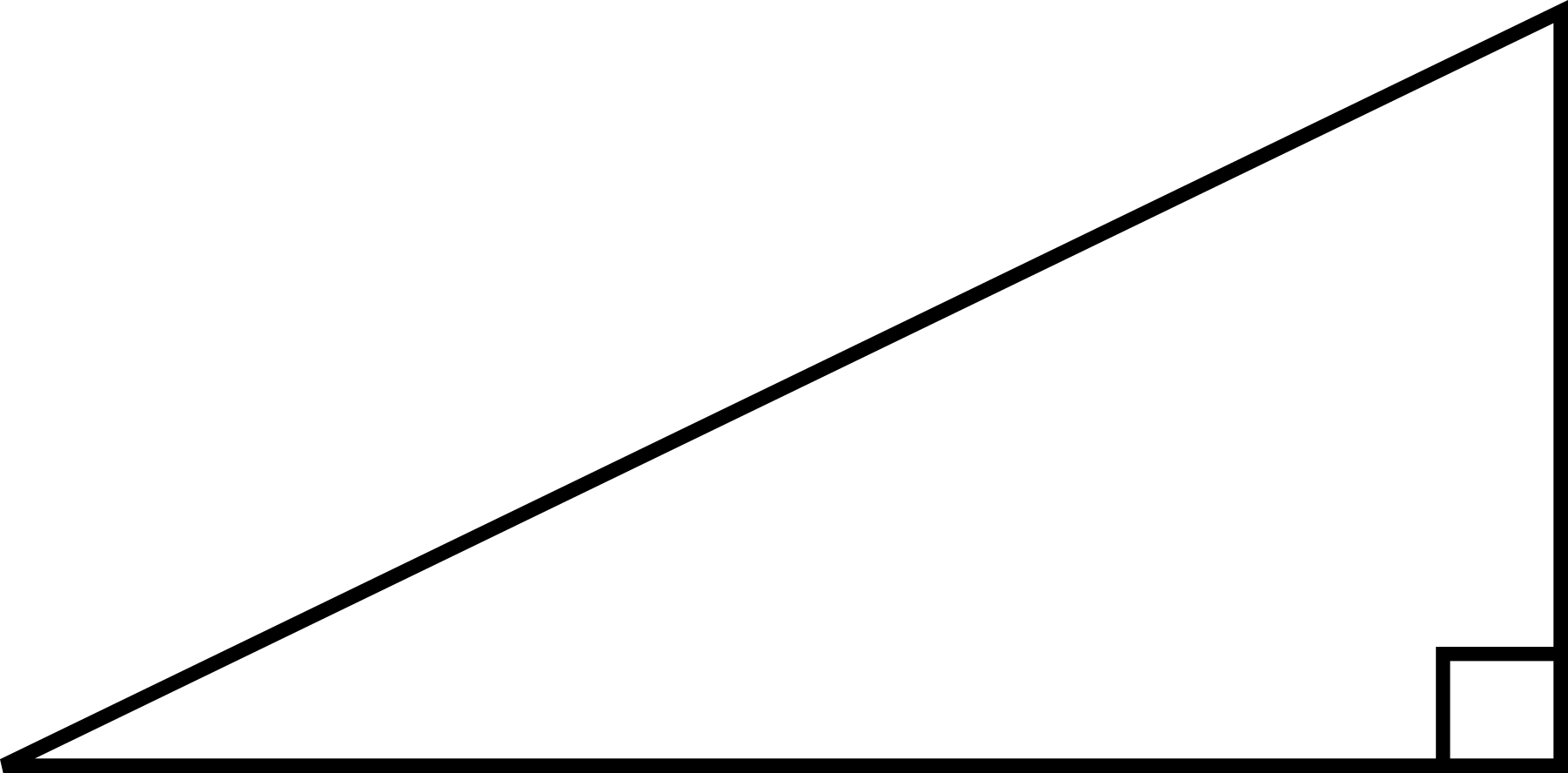
Theorem. If \(\Delta\) is a right triangle with side lengths \(c\geq b\geq a\), then \[a^{2}+b^{2}=c^{2}.\]

\(a\)

\(b\)

\(c\)

The Pythagorean Theorem

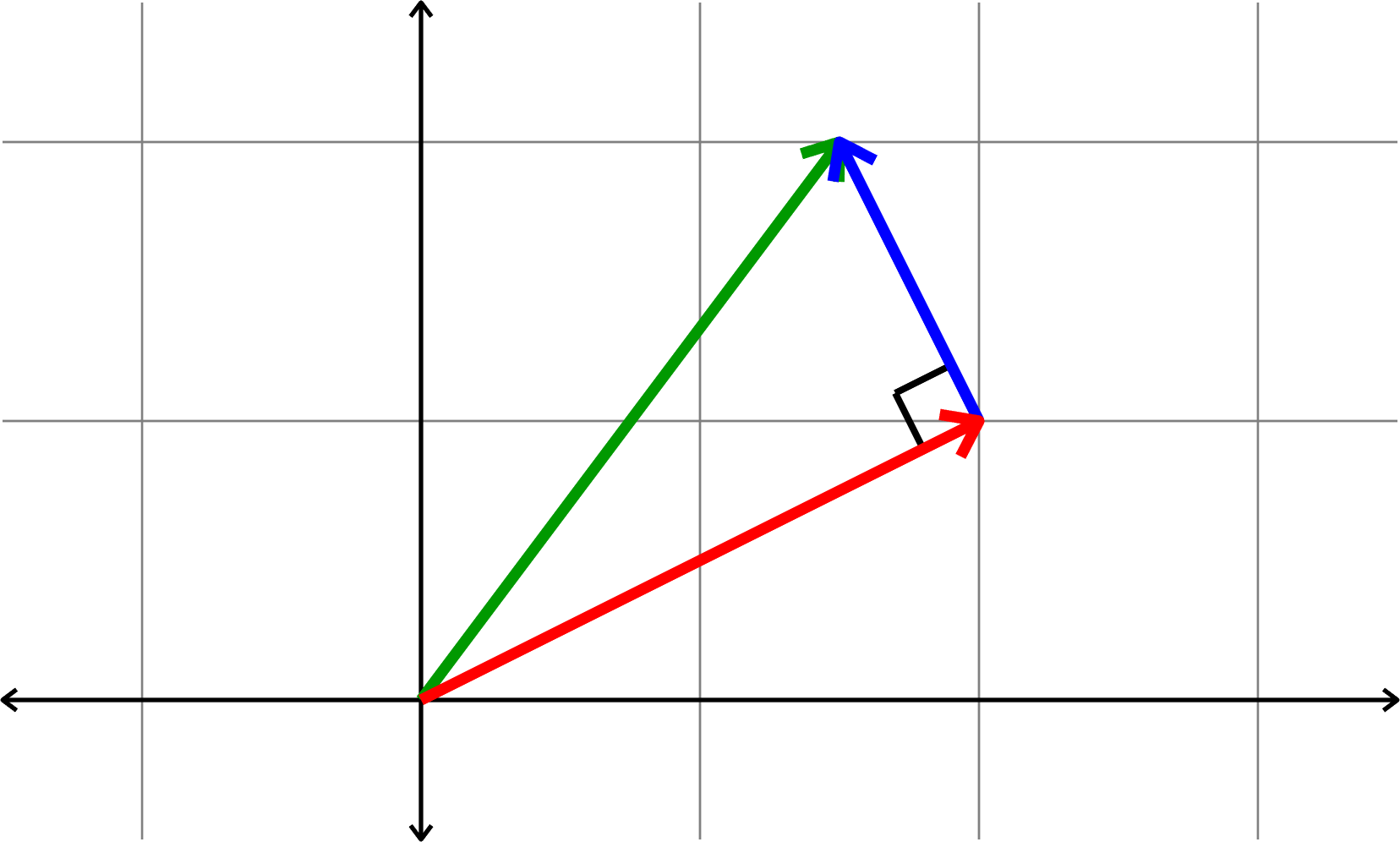
Theorem. If \(v\) and \(w\) are orthogonal vectors, then \[\|v\|^2 + \|w\|^2 = \|v+w\|^2.\]

\(v\)

\(w\)

\(v+w\)

The Pythagorean Theorem

(The Standard Generalization)

Theorem. If \(v_{1},v_{2},\ldots,v_{k}\) are pairwise orthogonal vectors, then

\[\|v_{1}\|^2 + \|v_{2}\|^2 + \cdots + \|v_{k}\|^{2} = \|v_{1}+v_{2}+\cdots+v_{k}\|^2.\]

Kadison's Observation

Kadison's Observation

Kadison's Observation

Kadison's Observation

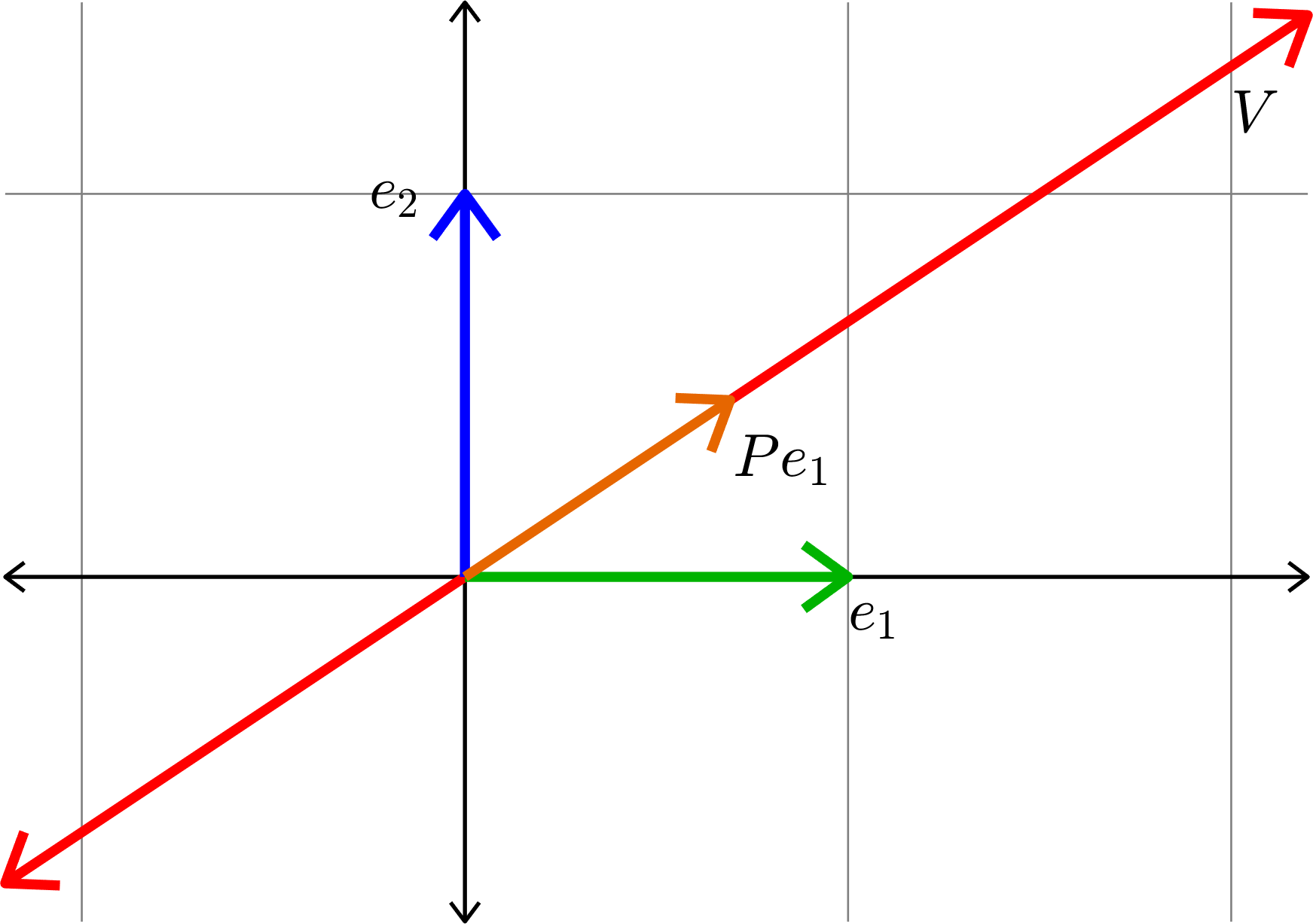
Kadison's Observation

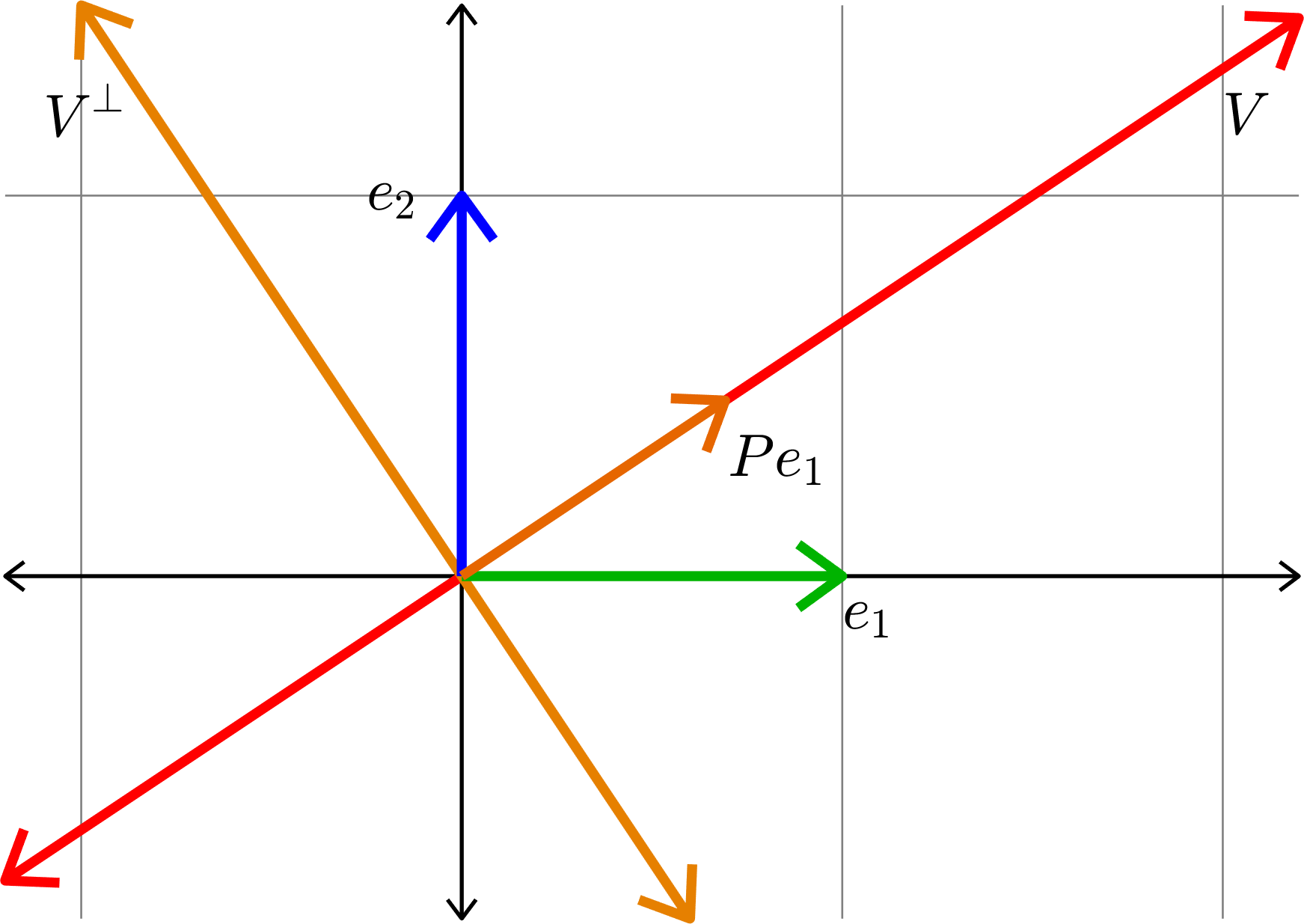
Kadison's Observation

Kadison's Observation

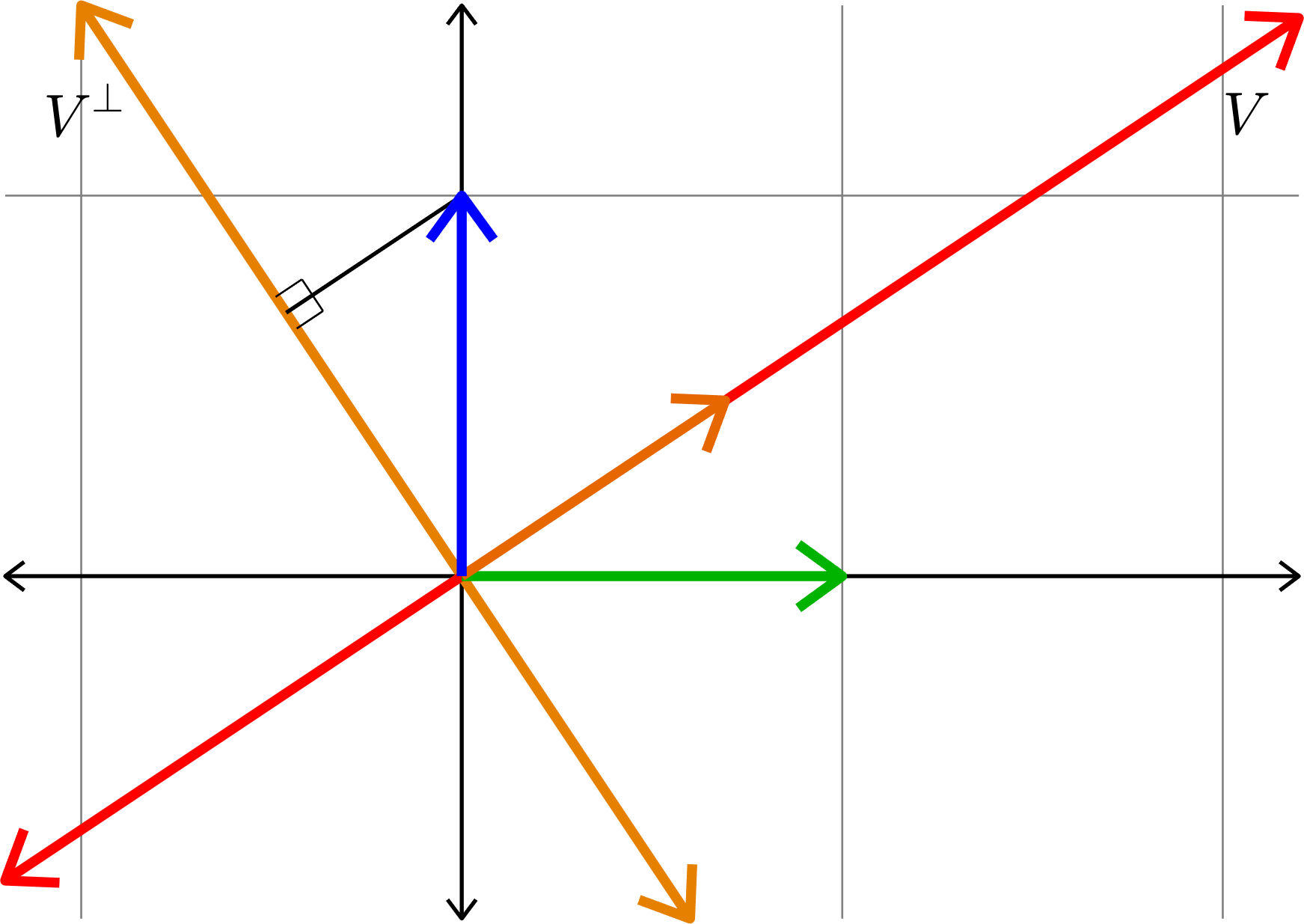
Kadison's Observation

Kadison's Observation

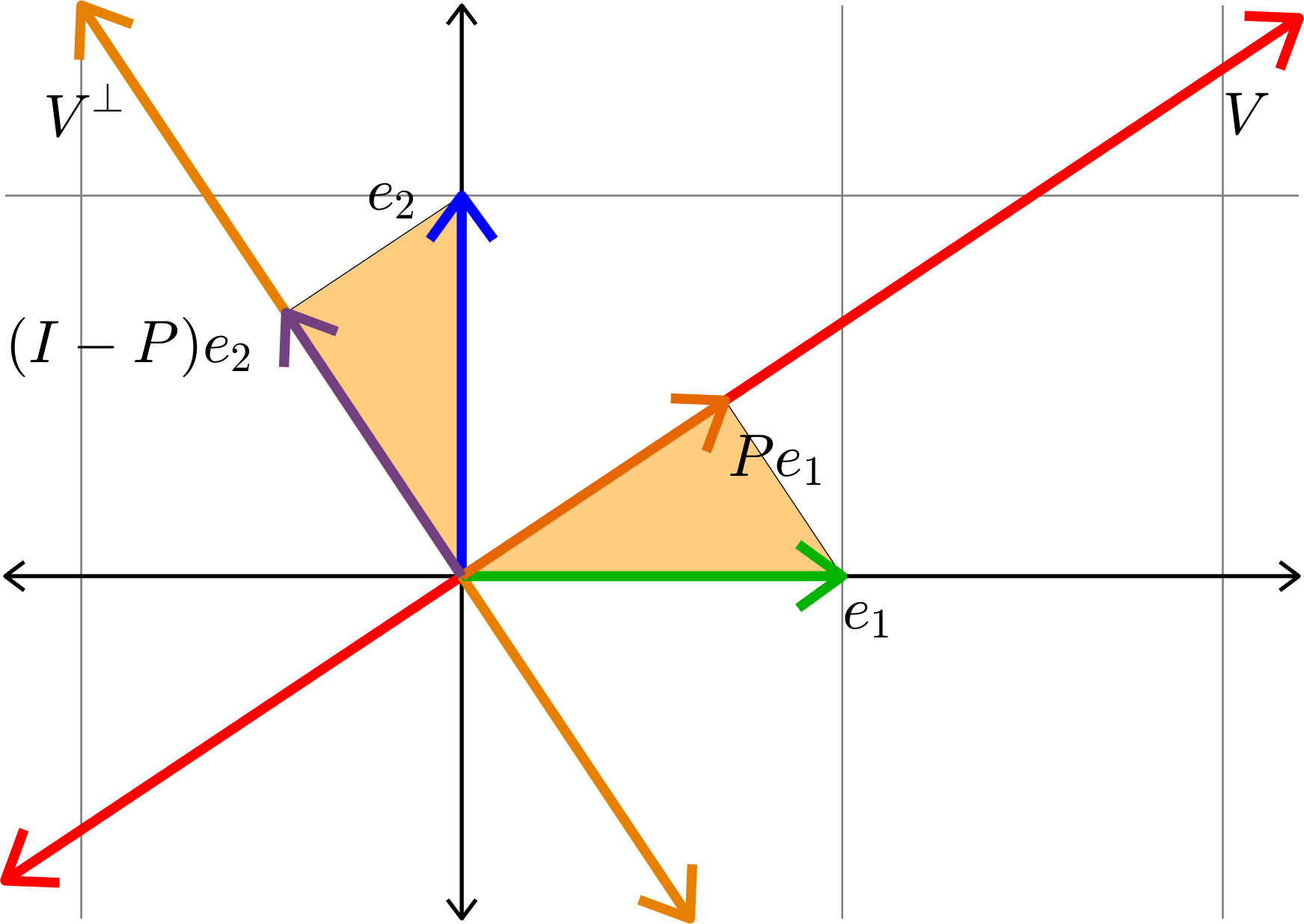
Similar Triangles!

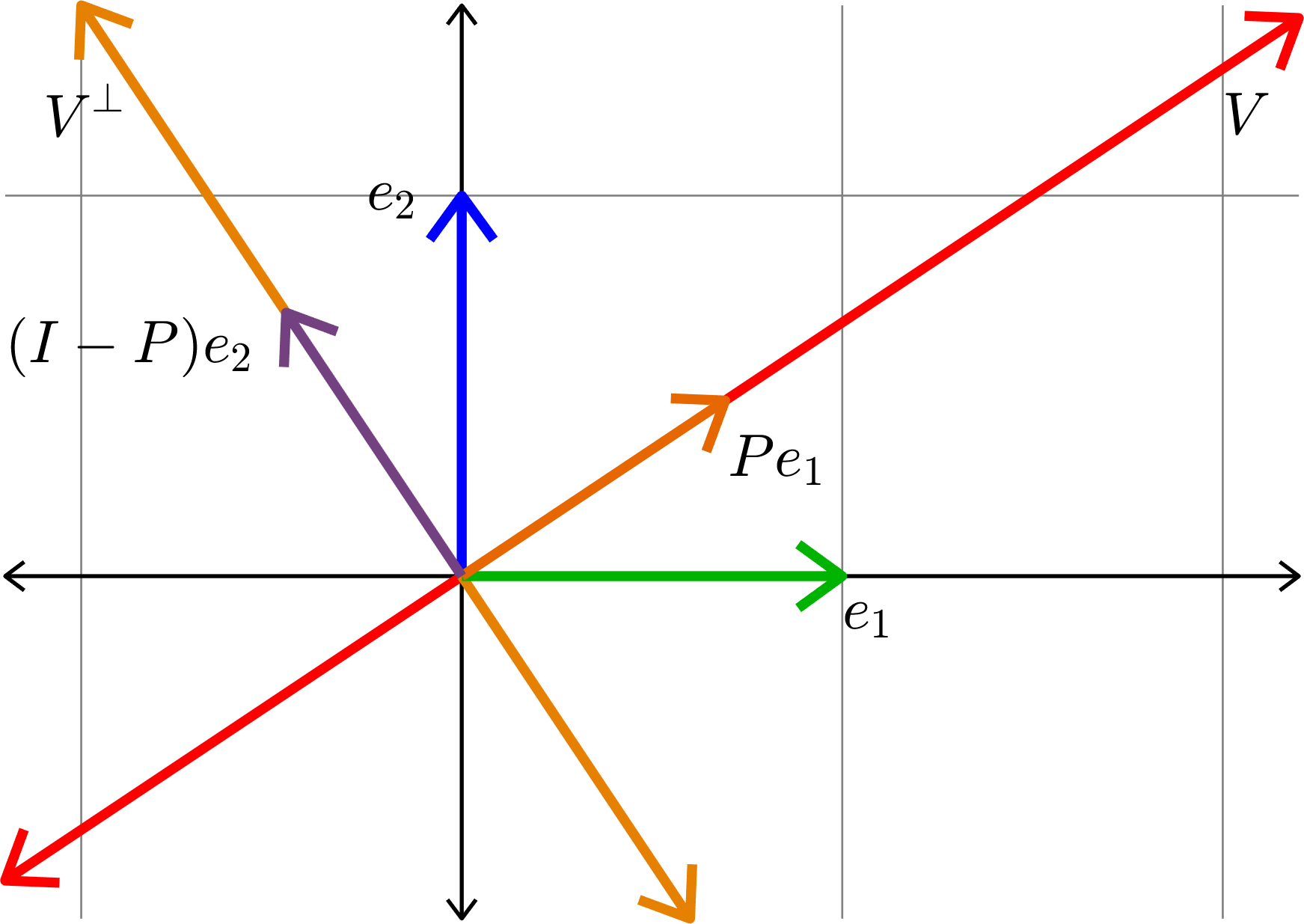
Kadison's Observation

Kadison's Observation

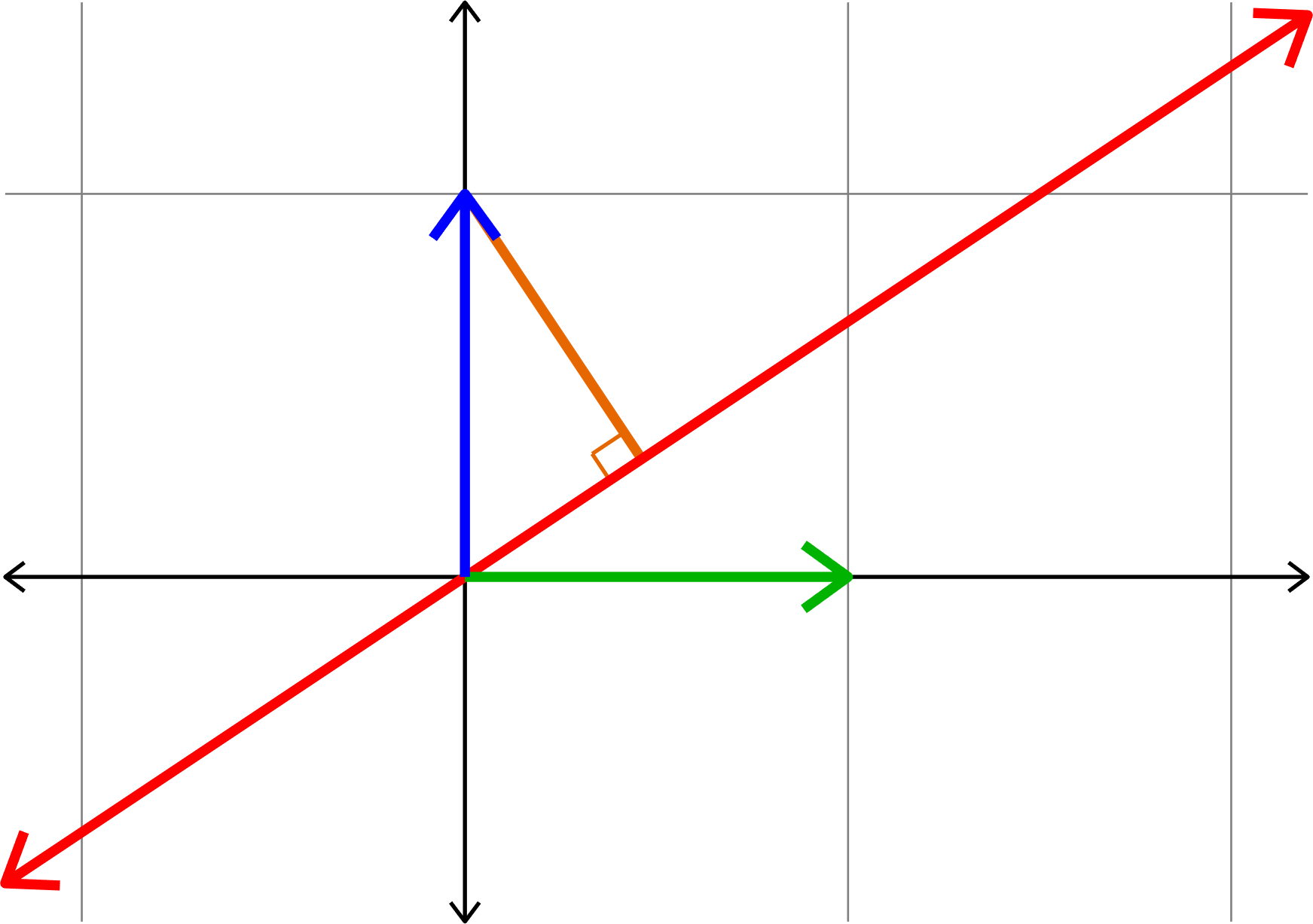
Kadison's Observation

Kadison's Observation

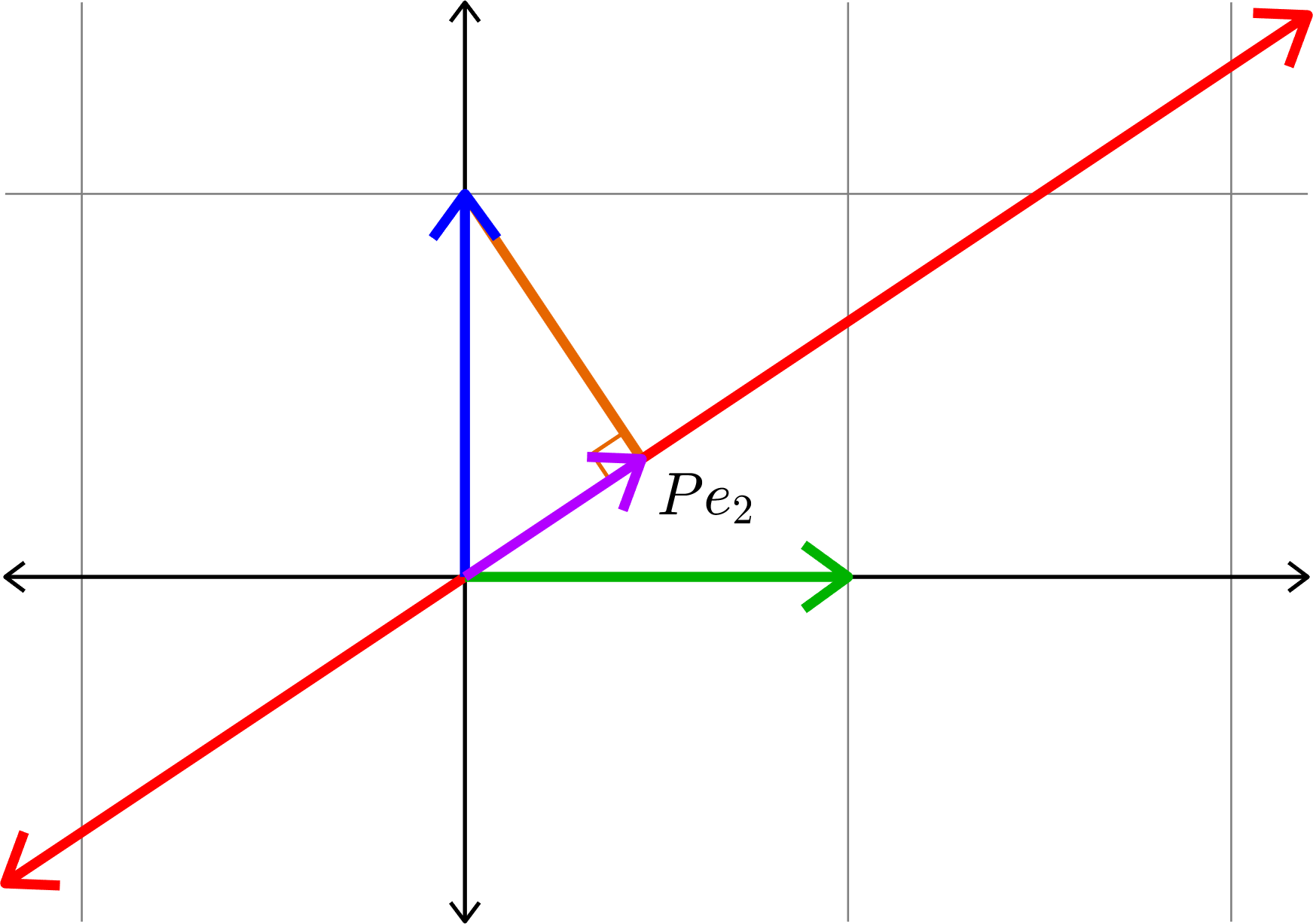
Kadison's Observation

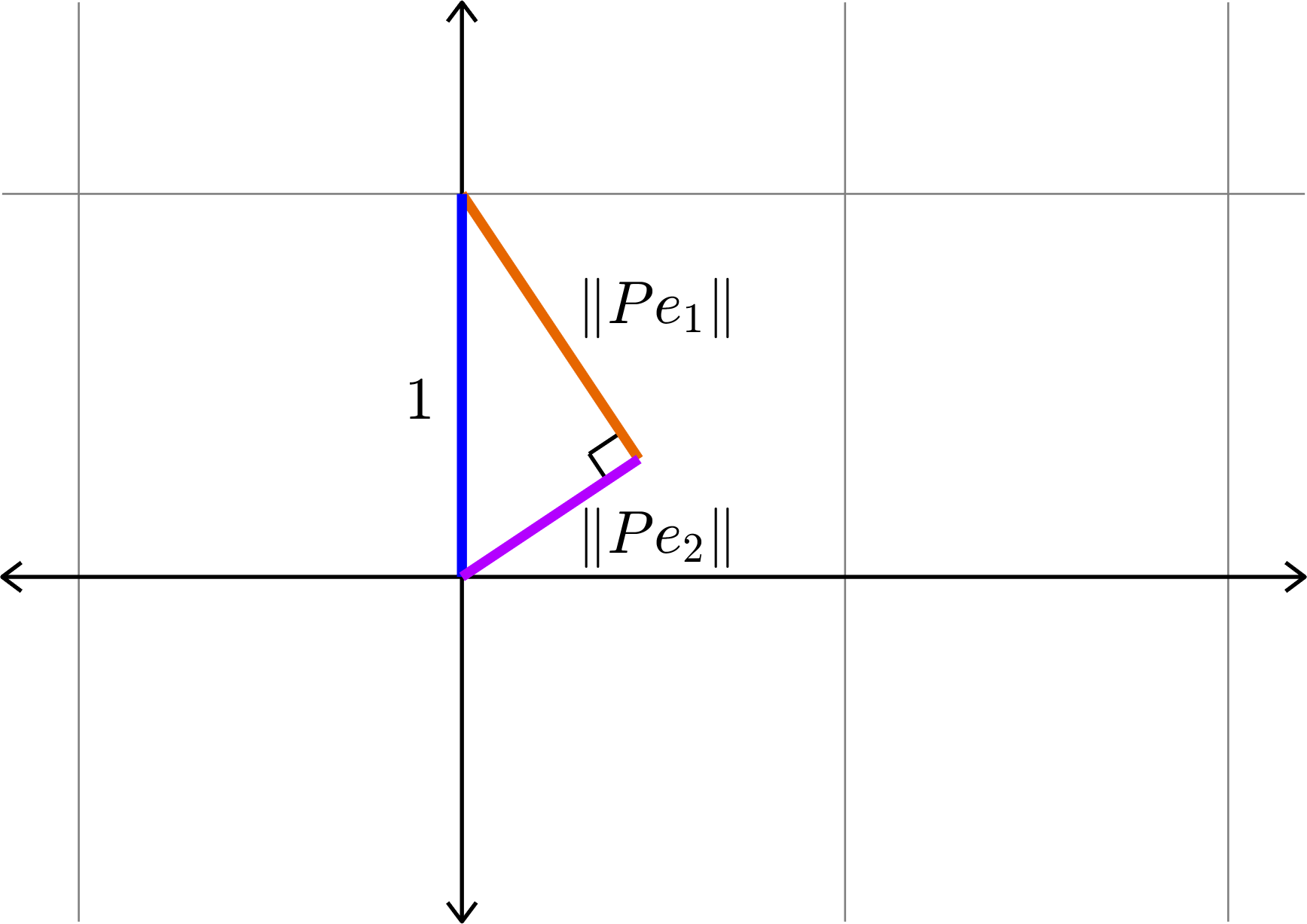
\[\|Pe_{1}\|^{2} + \|Pe_{2}\|^{2} = 1\]

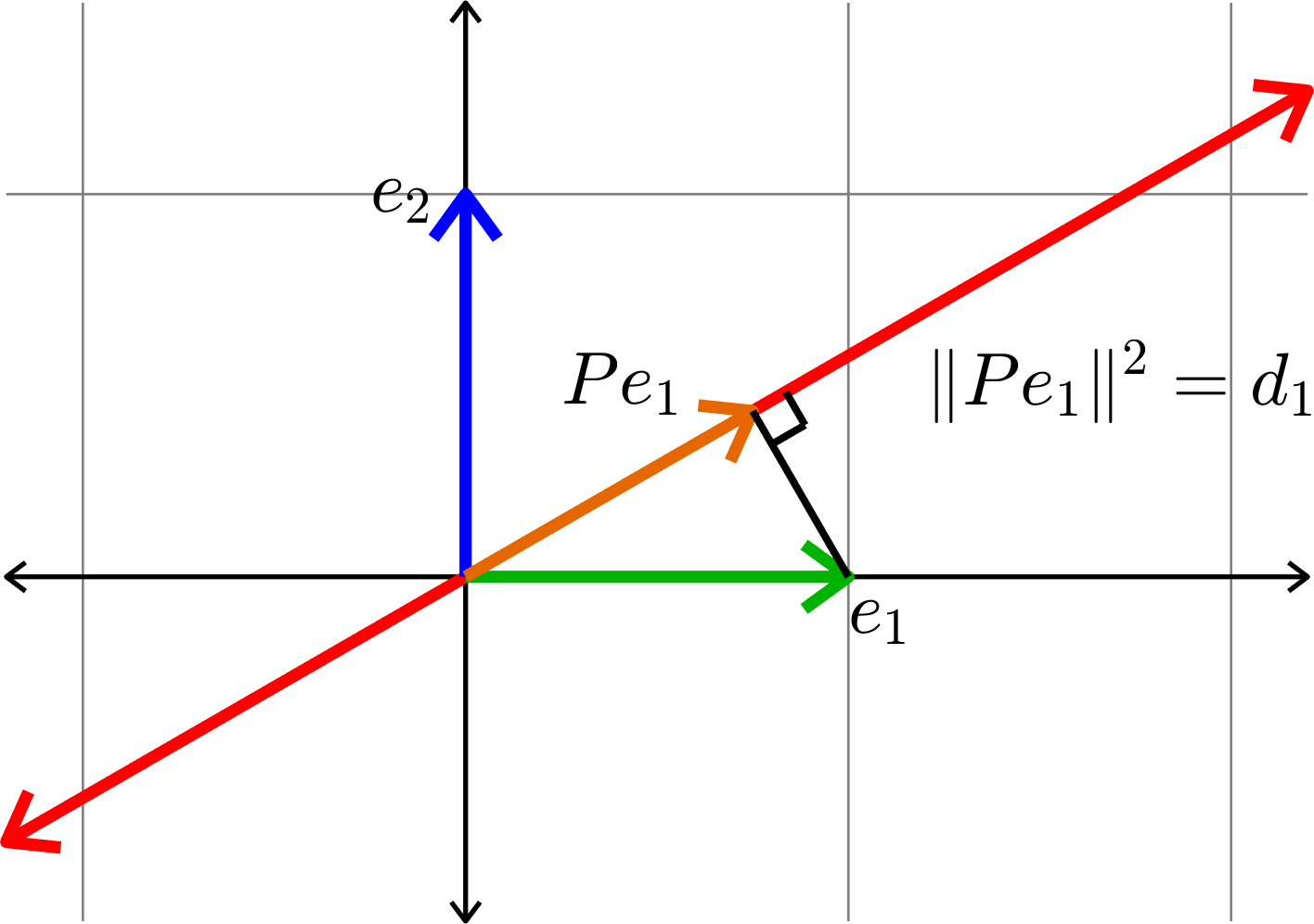
The Pythagorean Theorem 

Theorem. If \(P\) is an orthogonal projection onto a \(1\)-dimensional subspace \(V\), and \(\{e_{1},e_{2},\ldots,e_{n}\}\) is an orthonormal basis, then

\[\sum_{i=1}^{n}\|Pe_{i}\|^{2} = 1.\]

The Pythagorean Theorem and Diagonals

If \(P\) is an orthogonal projection onto a subspace \(V\), and \((e_{i})_{i=1}^{n}\) is an orthonormal basis, then

\[\|Pe_{i}\|^{2} = \langle Pe_{i},Pe_{i}\rangle = \langle P^{\ast}Pe_{i},e_{i}\rangle = \langle P^{2}e_{i},e_{i}\rangle = \langle Pe_{i},e_{i}\rangle\]

\[ = \left[\begin{array}{cccc} \|Pe_{1}\|^{2} & \ast & \cdots & \ast\\ \overline{\ast} & \|Pe_{2}\|^{2} & & \vdots\\ \vdots & & \ddots & \vdots\\ \overline{\ast} & \cdots & \cdots & \|Pe_{n}\|^{2}\end{array}\right] \]

\[P= \left[\begin{array}{cccc} \langle Pe_{1},e_{1}\rangle & \langle Pe_{2},e_{1}\rangle & \cdots & \langle Pe_{n},e_{1}\rangle \\ \langle Pe_{1},e_{2}\rangle & \langle Pe_{2},e_{2}\rangle & & \vdots\\ \vdots & & \ddots & \vdots\\ \langle Pe_{1},e_{n}\rangle & \cdots & \cdots & \langle Pe_{n},e_{n}\rangle \end{array}\right]\]

The Pythagorean Theorem 

Theorem. If \(P\) is an orthogonal projection onto a \(1\)-dimensional subspace \(V\), and \(\{e_{1},e_{2},\ldots,e_{n}\}\) is an orthonormal basis, then

\[\sum_{i=1}^{n}\|Pe_{i}\|^{2} = 1.\]

Proof. \[\sum_{i=1}^{n}\|Pe_{i}\|^{2} = \text{tr}(P) = \dim V = 1.\]

\(\Box\)

The Pythagorean Theorem 

Theorem. If \(P\) is an orthogonal projection onto a \(k\)-dimensional subspace \(V\), and \(\{e_{1},e_{2},\ldots,e_{n}\}\) is an orthonormal basis, then

\[\sum_{i=1}^{n}\|Pe_{i}\|^{2} = k.\]

Proof. \[\sum_{i=1}^{n}\|Pe_{i}\|^{2} = \text{tr}(P) = \dim V = k.\]

\(\Box\)

Kadison's Pythagorean Theorem (finite dimensional)

Theorem. If \(P\) is an orthogonal projection onto a \(k\)-dimensional subspace \(V\), and \(\{e_{1},e_{2},\ldots,e_{n}\}\) is an orthonormal basis, then

\[\sum_{i=1}^{n}\|Pe_{i}\|^{2} = k.\]

Proof. \[\sum_{i=1}^{n}\|Pe_{i}\|^{2} = \text{tr}(P) = \dim V = k.\]

\(\Box\)

The Carpenter's Theorem

Theorem. If \(\Delta\) is a triangle with side lengths \(c\geq b\geq a\), such that

\(a^{2}+b^{2}=c^{2},\) then \(\Delta\) is a right triangle. 

Theorem. If \(v\) and \(w\) are vectors in a real Hilbert space such that

\(\|v\|^2 + \|w\|^2 = \|v+w\|^2,\) then \(\langle v,w\rangle = 0.\)

The Carpenter's Theorem

Theorem. If \(d_{1},d_{2}\) are two numbers in \([0,1]\) such that \(d_{1}+d_{2} = 1,\) then there is a projection \(P\) such that \(d_{1} = \|Pe_{1}\|^2\) and \(d_{2} = \|Pe_{2}\|^2\), that is,

\[P = \begin{bmatrix} d_{1} & \alpha\\ \overline{\alpha} & d_{2}\end{bmatrix}.\]

Kadison's Carpenter's Theorem (2d)

Proof.

• By the intermediate value theorem there is a projection \(P\) such that \(\|Pe_{1}\|^{2}=d_{1}.\)
• By the Pythagorean theorem                \(\|Pe_{1}\|^2+\|Pe_{2}\|^2=1.\)
• Therefore, \[\|Pe_{2}\|^2=d_{2}.\]

Theorem. If \((d_{i})_{i=1}^{n}\) is a sequence of numbers in \([0,1]\) such that \[\sum_{i=1}^{n}d_{i}\in\N\cup\{0\},\] then there is an \(n\times n\) projection \(P\) such that \[\|Pe_{i}\|^{2} = d_{i} \quad\text{for}\quad i=1,\ldots,n.\]

Kadison's Carpenter's Theorem

Theorem. Assume \((d_{i})_{i=1}^{n}\) is a sequence of numbers in \([0,1].\) There is an \(n\times n\) projection \(P\) with diagonal \((d_{i})_{i=1}^{n}\) if and only if

\[\sum_{i=1}^{n}d_{i} \in\N\cup\{0\}.\]

Characterization of Diagonals of Projections

in Finite Dimensions

Diagonality

Definition. Given an operator \(E\) on a Hilbert space, a sequence \((d_{i})_{i\in I}\) is a diagonal of \(E\) if there is an orthonormal basis \((e_{i})_{i\in I}\) such that

\[d_{i} = \langle Ee_{i},e_{i}\rangle \quad\text{for all }i\in I.\]

Projections in infinite dimensions

Examples. Let \((e_{i})_{i=1}^{\infty}\) be an orthonormal basis.

Set \(\displaystyle{v = \sum_{i=1}^{\infty}\sqrt{\frac{1}{2^{i}}}e_{i}},\) then 

Projections in infinite dimensions

Examples. 

Theorem. Assume \((d_{i})_{i=1}^{n}\) is a sequence of numbers in \([0,1].\) There is an \(n\times n\) projection \(P\) with diagonal \((d_{i})_{i=1}^{n}\) if and only if

\[\sum_{i=1}^{n}d_{i} \in\N\cup\{0\}.\]

Diagonals of Projections Redux

Theorem. Assume \((d_{i})_{i=1}^{n}\) is a sequence of numbers in \([0,1].\) There is an \(n\times n\) projection \(P\) with diagonal \((d_{i})_{i=1}^{n}\) if and only if

\[\sum_{i=1}^{k}d_{i} - \sum_{i=k+1}^{n}(1-d_{i})\in\Z.\]

Diagonals of Projections Redux

Theorem (Kadison '02). Assume \((d_{i})_{i=1}^{\infty}\) is a sequence of numbers in \([0,1],\) and set 

\[a=\sum_{d_{i}<\frac{1}{2}}d_{i}\quad\text{and}\quad b=\sum_{d_{i}\geq \frac{1}{2}}(1-d_{i})\]

There is a projection \(P\) with diagonal \((d_{i})_{i=1}^{\infty}\) if and only if one of the following holds:

1. \(a=\infty\)
2. \(b=\infty\)
3. \(a,b<\infty\) and \(a-b\in\Z\)

Kadison's Theorem

Diagonals of \(2\times 2\) self-adjoint matrices

Up to unitary equivalence \(E=\begin{bmatrix} \lambda_{1} & 0\\ 0 & \lambda_{2}\end{bmatrix}\), with \(\lambda_{1}\geq \lambda_{2}\).

\[\begin{bmatrix}\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta\end{bmatrix}\begin{bmatrix} \lambda_{1} & 0\\ 0 & \lambda_{2}\end{bmatrix}\begin{bmatrix}\cos\theta & \sin\theta\\ -\sin\theta & \cos\theta\end{bmatrix}\]

\[= \begin{bmatrix}\alpha\lambda_{1}+(1-\alpha)\lambda_{2} & \ast\\ \overline{\ast} & (1-\alpha)\lambda_{1} + \alpha\lambda_{2} \end{bmatrix},\quad (\alpha = \cos^{2}\theta)\]

Givens rotations

\[\begin{bmatrix}\cos\theta & -\sin\theta & 0\\ \sin\theta & \cos\theta & 0\\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix} \lambda_{1} & 0 & 0\\ 0 & \lambda_{2} & 0\\ 0 & 0 & \lambda_{3}\end{bmatrix}\begin{bmatrix}\cos\theta & \sin\theta & 0\\ -\sin\theta & \cos\theta & 0\\ 0 & 0 & 1\end{bmatrix}\]

\[= \begin{bmatrix}\alpha\lambda_{1}+(1-\alpha)\lambda_{2} & \ast & 0\\ \overline{\ast} & (1-\alpha)\lambda_{1} + \alpha\lambda_{2} & 0\\ 0 & 0 & \lambda_{3}\end{bmatrix},\quad (\alpha = \cos^{2}\theta)\]

Suppose \(E = \left[\begin{smallmatrix} \lambda_{1} & 0 & 0\\ 0 & \lambda_{2} & 0\\ 0 & 0 & \lambda_{3}\end{smallmatrix}\right]\) with \(\lambda_{1}\geq \lambda_{2}\geq\lambda_{3}\)

Diagonals of \(3\times 3\) & \(4\times 4\) self-adjoint matrices

Suppose \(E = \left[\begin{smallmatrix} \lambda_{1} & 0 & 0\\ 0 & \lambda_{2} & 0\\ 0 & 0 & \lambda_{3}\end{smallmatrix}\right]\) with \(\lambda_{1}\geq \lambda_{2}\geq\lambda_{3}\)

Then \((d_{1},d_{2},d_{3})\), with \(d_{1}\geq d_{2}\geq d_{3}\) is a diagonal of \(E\) if and only if

\[d_{i}\in\operatorname{conv}\{\lambda_{1},\lambda_{2},\lambda_{3}\}\quad\forall\,i\]

and

\[d_{1}+d_{2}+d_{3}=\lambda_{1}+\lambda_{2}+\lambda_{3}.\]

The Schur-Horn Theorem

Theorem (Schur '23, Horn '54). Let \((d_{i})_{i=1}^{n}\) and \((\lambda_{i})_{i=1}^{n}\) be nonincreasing sequences. There is a self-adjoint matrix \(E\) with diagonal \((d_{i})_{i=1}^{n}\) and eigenvalues \((\lambda_{i})_{i=1}^{n}\) if and only if

\[\sum_{i=1}^{k}d_{i}\leq \sum_{i=1}^{k}\lambda_{i}\quad\text{for}\quad k=1,2,\ldots,n-1\]

and

\[\sum_{i=1}^{n}d_{i} = \sum_{i=1}^{n}\lambda_{i}.\]

(1)

(2)

Theorem (Arveson, Kadison '06, Kaftal, Weiss '10). Let \((\lambda_{i})_{i=1}^{\infty}\) be a positive nonincreasing sequence, and let \((d_{i})_{i=1}^{\infty}\) be a nonnegative nonincreasing sequence. There exists a positive compact operator with positive eigenvalues \((\lambda_{i})_{i=1}^{\infty}\) and diagonal \((d_{i})_{i=1}^{\infty}\) if and only if

\[\sum_{i=1}^{k}d_{i}\leq \sum_{i=1}^{k}\lambda_{i}\quad\text{for all}\quad k\in\N\]

and

\[\sum_{i=1}^{\infty}d_{i} = \sum_{i=1}^{\infty}\lambda_{i}.\]

Non-positive operators

Example. Consider the diagonal matrix \(E = \operatorname{diag}(-1,1,\frac{1}{2},\frac{1}{4},\frac{1}{8},\ldots)\)

\[\begin{bmatrix} -1 & 0 & 0 & 0 & \cdots\\ 0 & 1 & 0 & 0 & \cdots\\ 0 & 0 & \frac{1}{2} & 0 & \cdots\\ 0 & 0 & 0 & \frac{1}{4}\\ \vdots & \vdots & \vdots & & \ddots\end{bmatrix} \simeq \begin{bmatrix} -\frac{1}{2} & \ast & 0 & 0 & \cdots\\ \overline{\ast} & \frac{1}{2} & 0 & 0 & \cdots\\ 0 & 0 & \frac{1}{2} & 0 & \cdots\\ 0 & 0 & 0 & \frac{1}{4}\\ \vdots & \vdots & \vdots & & \ddots\end{bmatrix} \simeq \begin{bmatrix} -\frac{1}{4} & \ast & \ast & 0 & \cdots\\ \overline{\ast} & \frac{1}{2} & \ast & 0 & \cdots\\ \overline{\ast} & \overline{\ast} & \frac{1}{4} & 0 & \cdots\\ 0 & 0 & 0 & \frac{1}{4}\\ \vdots & \vdots & \vdots & & \ddots\end{bmatrix}\]

\[\simeq\cdots\simeq \begin{bmatrix} 0 & \ast & \ast & \ast & \cdots\\ \overline{\ast} & \frac{1}{2} & \ast & \ast & \cdots\\ \overline{\ast} & \overline{\ast} & \frac{1}{4} & \ast & \cdots\\ \overline{\ast} & \overline{\ast} & \overline{\ast} & \frac{1}{8}\\ \vdots & \vdots & \vdots & & \ddots\end{bmatrix}\]

Definition. Let \(\boldsymbol\lambda =\{\lambda_i\}_{i\in I}\in c_0\). Define its positive part \(\boldsymbol\lambda_+ =\{\lambda^{+}_i\}_{i\in I}\) by \(\lambda^+_i=\max(\lambda_i,0)\). The negative part is defined as \(\boldsymbol\lambda_-=(-\boldsymbol \lambda)_+.\)
If \(\boldsymbol\lambda \in c_0^+\), then define its decreasing rearrangement \(\boldsymbol\lambda^{\downarrow} =\{\lambda^{\downarrow}_i\}_{i\in \N}\) by taking \(\lambda^{\downarrow}_i\) to be the \(i\)th largest term of \(\boldsymbol \lambda.\) For the sake of brevity, we will denote the \(i\)th term of \((\boldsymbol\lambda_{+})^{\downarrow}\) by \(\lambda_{i}^{+\downarrow}\), and similarly for \((\boldsymbol\lambda_{-})^{\downarrow}\).

\[-\lambda^{-\downarrow}_{1}\leq -\lambda^{-\downarrow}_{2}\leq-\lambda^{-\downarrow}_{3}\leq\cdots\leq 0\leq\cdots\leq \lambda^{+\downarrow}_{3}\leq \lambda^{+\downarrow}_{2}\leq \lambda^{+\downarrow}_{1}\]

Hence, we have "rearranged" the sequence \(\boldsymbol\lambda\) as follows:

Note:

If \(\boldsymbol\lambda\) has infinitely many positive terms, then \(\boldsymbol\lambda_{+}\) has no zeros.

If \(\boldsymbol\lambda\) has finitely many positive terms, then \(\boldsymbol\lambda_{+}\) has infinitely many zeros.

Rearranging sequences

Excess

Given a compact self-adjoint operator \(E\) with eigenvalue list \(\boldsymbol\lambda\), it is straightforward to show that if \(\boldsymbol{d}\in c_{0}\) is a diagonal of \(E\), then

\[\sum_{i=1}^n \lambda_i^{+ \downarrow} \geq \sum_{i=1}^n d_i^{+ \downarrow} \quad\text{and }\quad \sum_{i=1}^n \lambda_i^{- \downarrow} \ge \sum_{i=1}^n d_i^{- \downarrow} \qquad\text{for all }k\in \N,\]

But it is not true that

\[\sum_{i=1}^\infty d_{i}^{+} = \sum_{i=1}^{\infty}\lambda_{i}^{+}\quad\text{and}\quad \sum_{i=1}^\infty d_{i}^{-} = \sum_{i=1}^{\infty}\lambda_{i}^{-}\]

Indeed, \((0,\frac{1}{2},\frac{1}{4},\frac{1}{8},\ldots)\) is a diagonal of an operator with eigenvalue list \((-1,1,\frac{1}{2},\frac{1}{4},\frac{1}{8},\ldots)\).

We need to keep track of how much "mass" was moved across zero:

Theorem (Bownik, J '22) Let \(\boldsymbol\lambda,\boldsymbol{d}\in c_{0}\). Set

\[\sigma_{+} = \liminf_{n\to\infty} \sum_{i=1}^n (\lambda_i^{+ \downarrow} - d_i^{+ \downarrow})\quad\text{and}\quad \sigma_{-} = \liminf_{n\to\infty} \sum_{i=1}^n (\lambda_i^{- \downarrow} - d_i^{- \downarrow})\]

Let \(A\) be a compact self-adjoint operator with eigenvalue list \(\boldsymbol\lambda.\)

The sequence \(\boldsymbol d\) is a diagonal of an operator \(B\) such that \(A\oplus \boldsymbol 0\) and

\(B \oplus \boldsymbol 0\) are unitarily equivalent, where \(\boldsymbol 0\) denotes the zero operator on an infinite dimensional Hilbert space, if and only if the following four conditions hold:

\[\sum_{i=1}^n \lambda_i^{+ \downarrow} \geq \sum_{i=1}^n d_i^{+ \downarrow} \quad\text{and }\quad \sum_{i=1}^n \lambda_i^{- \downarrow} \ge \sum_{i=1}^n d_i^{- \downarrow} \qquad\text{for all }k\in \N,\]

\[\boldsymbol d_+ \in \ell^1 \quad \implies\quad \sigma_{-}\geq \sigma_{+}.\]

\[\boldsymbol d_- \in \ell^1 \quad \implies\quad  \sigma_{+}\geq \sigma_{-}\]

Note: If \(\boldsymbol d\in\ell^{1}\) (\(A\) is trace class), then \(\sigma_{-} = \sigma_{+}\). That is \(\sum d_{i} = \sum\lambda_{i}\).

Theorem (Bownik, J '22) Let \(\boldsymbol\lambda,\boldsymbol{d}\in c_{0}\).  Let \(A\) be a compact self-adjoint operator with eigenvalue list \(\boldsymbol\lambda.\) If

\[\sum_{i=1}^n \lambda_i^{+ \downarrow} \geq \sum_{i=1}^n d_i^{+ \downarrow} \quad\text{and }\quad \sum_{i=1}^n \lambda_i^{- \downarrow} \ge \sum_{i=1}^n d_i^{- \downarrow} \qquad\text{for all }k\in \N,\]

and

\[\sigma_{+}=\sigma_{-}\in(0,\infty).\]

then, the sequence \(\boldsymbol d\) is a diagonal of \(A\).

In some special cases we can get a stronger sufficiency result:

Where did it go?

Example. Set \[\boldsymbol\lambda = \left(-1,1,\frac{1}{2},\frac{1}{4},\frac{1}{8},\ldots\right)\] and \[\boldsymbol{d} =\left (\frac{1}{2},\frac{1}{4},\frac{1}{8},\ldots\right)\]

Then \[\sigma_{+}=\sigma_{-}=1\in(0,\infty),\] and clearly

\[\sum_{i=1}^n \lambda_i^{+ \downarrow} \geq \sum_{i=1}^n d_i^{+ \downarrow} \quad\text{and }\quad \sum_{i=1}^n \lambda_i^{- \downarrow} \ge \sum_{i=1}^n d_i^{- \downarrow} \qquad\text{for all }k\in \N,\]

So, \((0,\frac{1}{2},\frac{1}{4},\frac{1}{8},\cdots)\) and \((\frac{1}{2},\frac{1}{4},\frac{1}{8},\cdots)\) are diagonals of \(E=\operatorname{diag}(\boldsymbol\lambda)\).

Thanks!

• This work was partially supported by NSF #1830066
• Webpage: https://sites.google.com/view/john-jasper-math/home
• Slides: https://slides.com/johnjasper