Analytics Chapter
Support Vector Machines
Author: Jose Miguel Arrieta Ramos
Intuition
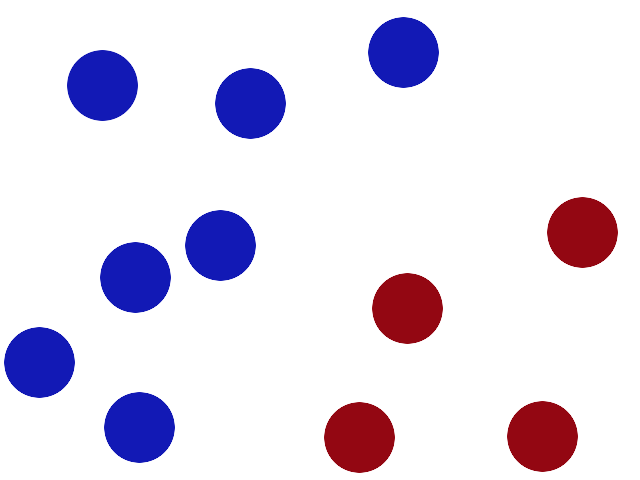
We have 2 colors of balls on the table that we want to separate.
Intuition
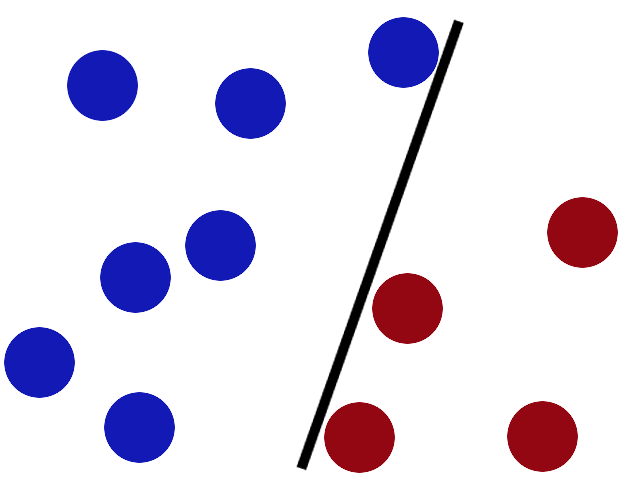
We get a stick and put it on the table, this works pretty well right?
Intuition
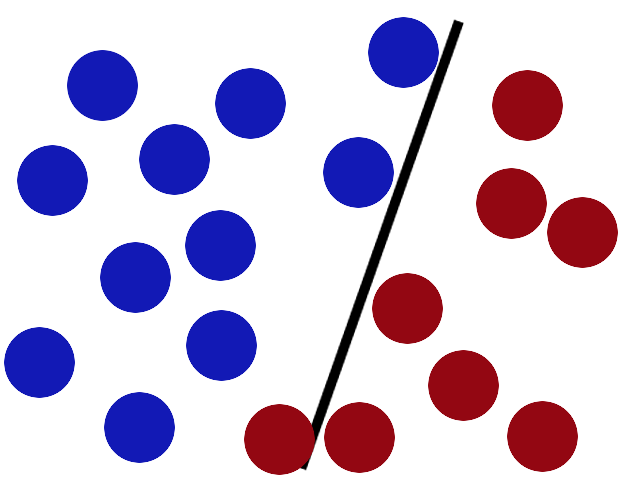
Some villain comes and places more balls on the table, it kind of works but one of the balls is on the wrong side and there is probably a better place to put the stick now.
Intuition
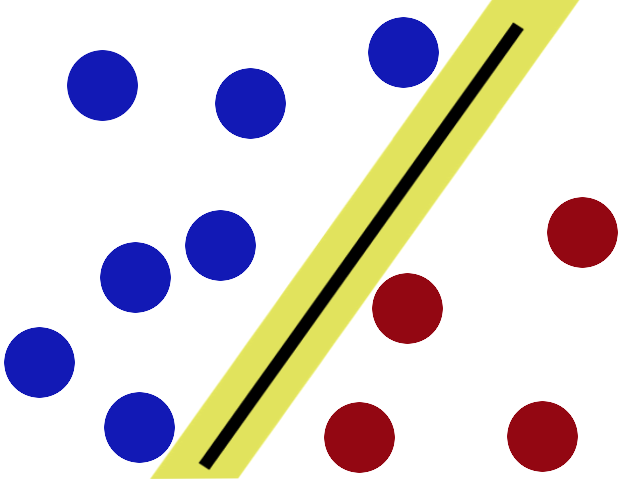
SVMs try to put the stick in the best possible place by having as big a gap on either side of the stick as possible.
Intuition
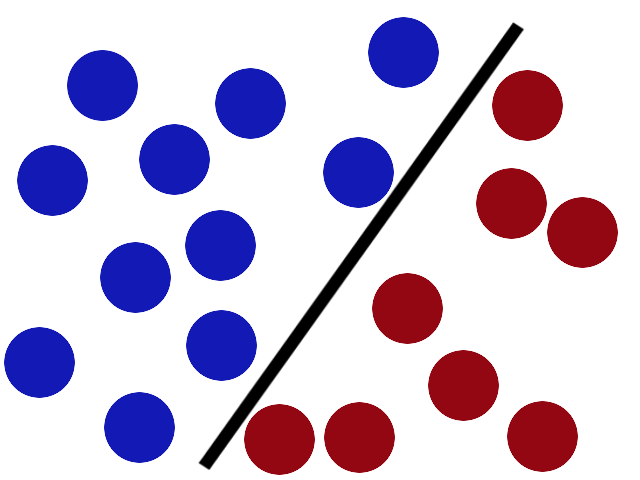
Now when the villain returns the stick is still in a pretty good spot
Intuition

Say the villain has seen how good you are with a stick so he gives you a new challenge.
Intuition

There’s no stick in the world that will let you split those balls well, so what do you do? You flip the table of course! Throwing the balls into the air. Then, with your pro ninja skills, you grab a sheet of paper and slip it between the balls.
Intuition

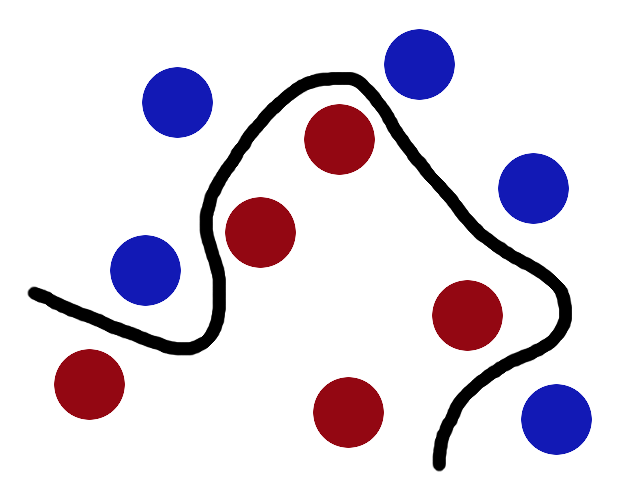
Now, looking at the balls from where the villain is standing, they balls will look split by some curvy line.
Summary
balls = data
stick = classifier
biggest gap trick = optimization
flipping the table = kernelling
piece of paper = hyperplane.
SVM
" Intuitively, a good separation is achieved by the hyperplane that has the largest distance to the nearest training-data point of any class (so-called functional margin), since in general the larger the margin the lower the generalization error of the classifier."
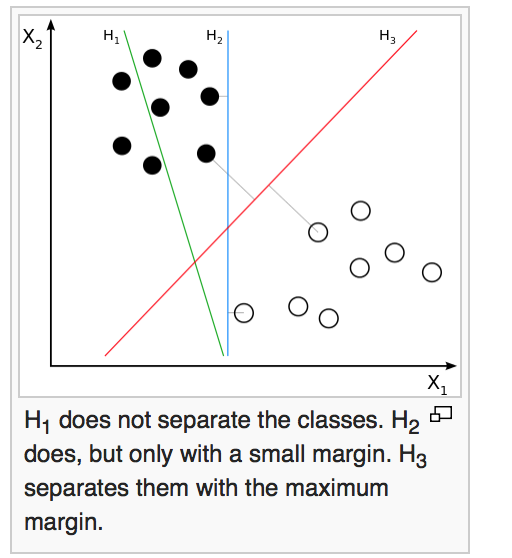
Hard-Margin
If the training data are linearly separable, we can select two parallel hyperplanes that separate the two classes of data, so that the distance between them is as large as possible.
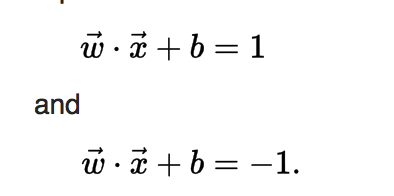
These hyperplanes can be described by the equations:

Geometrically, the distance between these two hyperplanes is
so to maximize the distance between the planes we want to minimize
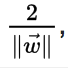
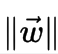
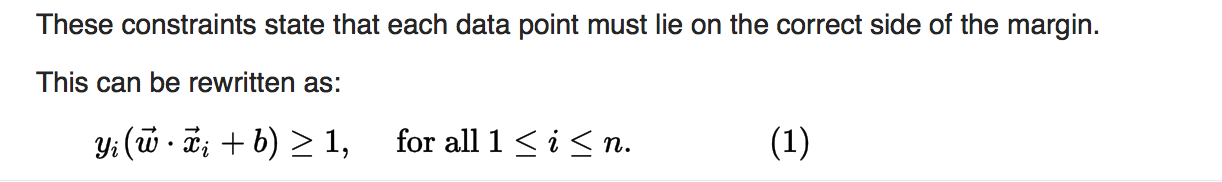
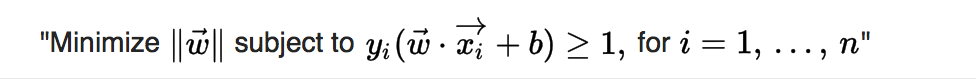
As we also have to prevent data points from falling into the margin, we add the following constraint:
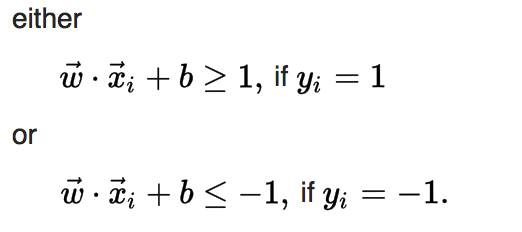
* To sum up:
Text
Linear separability
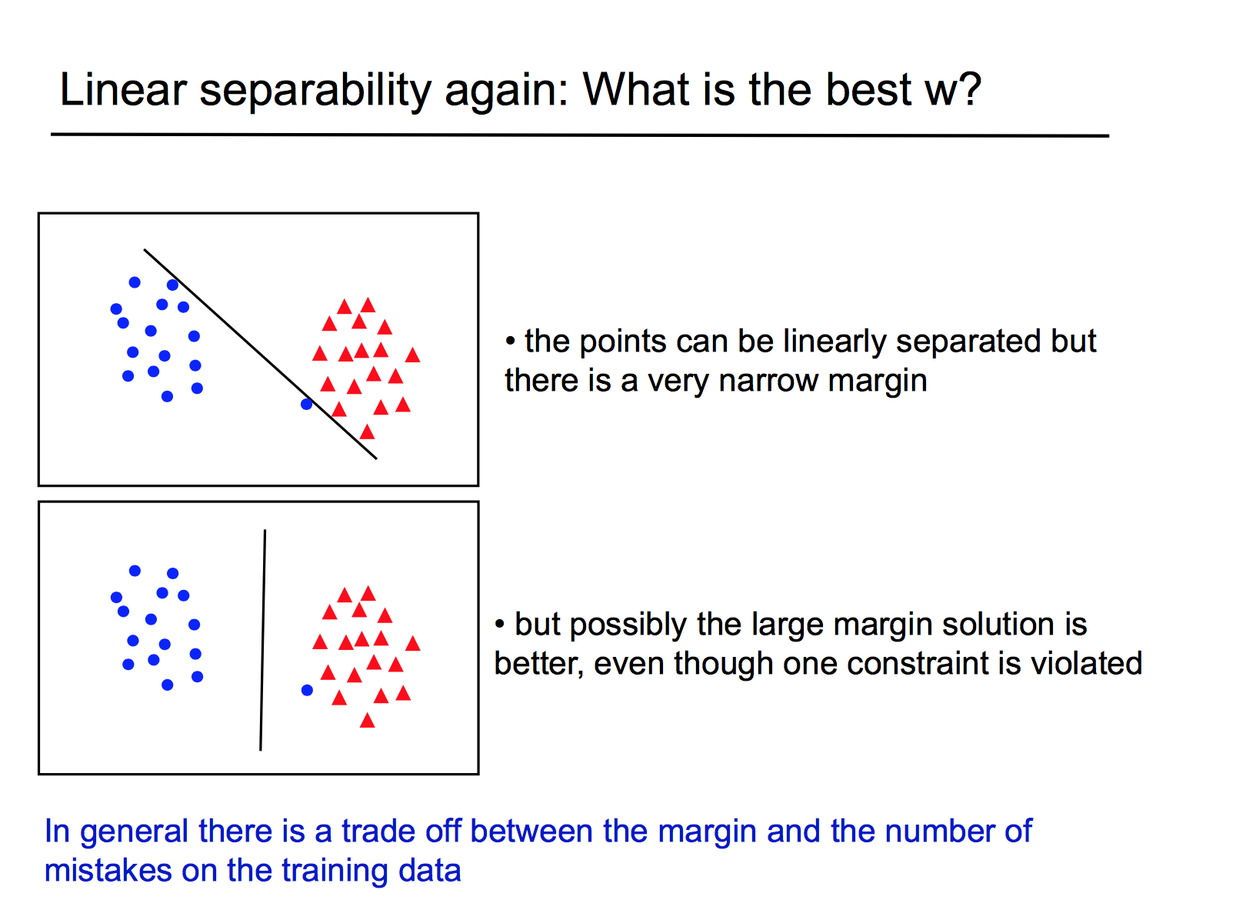
Soft-Margin
Hinge loss: The cumulated hinge loss is therefore an upper bound of the number of mistakes made by the classifier
To extend SVM to cases in which the data are not linearly separable, we introduce the hinge loss function:
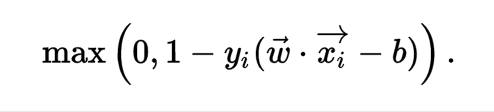
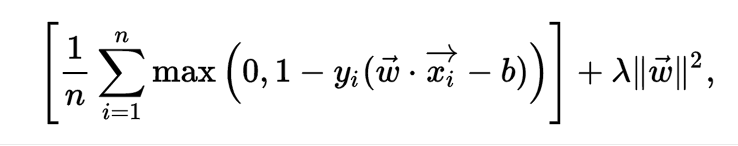
We then wish to minimize:
from sklearn.svm import SVC
import numpy as np
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
y = np.array([1, 1, 2, 2])
clf = SVC()
clf.fit(X, y)
print(clf.predict([[-0.8, -1]]))Real Example
Classify Voces from Young Female VS MiddleAge Males (US)
Pipeline:
- Download 500 .wav files (250 from female 250 from Male)
- Pre-process audio samples
- Extract Features (MFCC,delta1,delta2)
- Create feature representation of samples (Bag of Features)
- Reduce dimensionality (tSNE)
- SVM
- Stratified cross validation (k-folds)
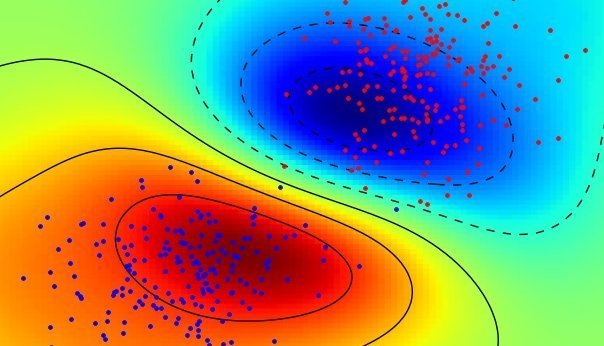
Graph Dimensionality reduction (tSNE)
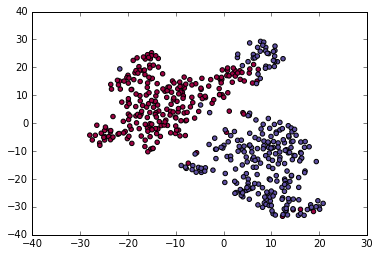
Young Female-us
MiddleAge Males-us
Plot differents SVM
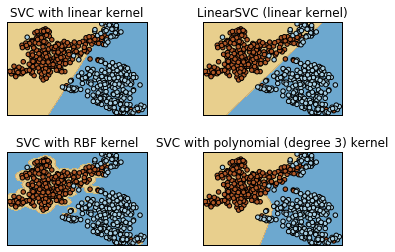
Results
- Stratified Cross Validation (k=10 folds, svm lineal kernel,1 run).
- Accuracie: 93.4
- AUC: 93.4
THANKS!!
Copy of deck
By Jose Arrieta
Copy of deck
- 572
